World Journal of Mechanics
Vol.06 No.07(2016), Article ID:69294,15 pages
10.4236/wjm.2016.67017
Experimental Investigation of Discharge Capacity of Labyrinth Weirs with and without Nappe Breakers
Omer Bilhan1, M. Emin Emiroglu2, Carol J. Miller3*
1Department of Civil Engineering, Nevsehir HBV University, Nevsehir, Turkey
2Department of Civil Engineering, Firat University, Elazig, Turkey
3Department of Civil and Environmental Engineering, Wayne State University, Detroit, MI, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2016; accepted 26 July 2016; published 29 July 2016
ABSTRACT
Labyrinth weirs provide higher discharge capacity than conventional weirs, with the ability to pass large flows at comparatively low heads. Labyrinth weirs are primarily used as spillways for dams where the spillway width is restricted. In recent years, many research investigations have considered the hydraulic performance of labyrinth weirs, particularly as dependent on the geometric features. The previous work has improved the design basis for such weirs. However, their design still requires experimentally derived and generalized performance curves. It is especially important to observe the behavior of the weir nappe to ensure the design provides hydraulic optimization and to account for pressure fluctuations, possible vibrations, resonance effect, noise and flow surging. In the present study, discharge coefficients were experimentally determined for both circular labyrinth weirs and sharp crested trapezoidal labyrinth weirs of varying side wall angle (α). Additional studies were completed with nappe breakers included to reduce the impact of vibration on the labyrinth weirs. In general, the test data indicated that nappe breakers placed on the trapezoidal labyrinth weirs and circular labyrinth weirs reduced the discharge coefficient by up to 4% of the un-amended weir.
Keywords:
Weir, Discharge Coefficient, Trapezoidal, Circular, Labyrinth Weir, Nappe Breaker

1. Introduction
Labyrinth weirs provide an effective means to increase the spillway discharge capacity of dams and are often considered for renovation projects required due to an increase in expected flood inflow to the reservoir of an existing dam. Due to the complex design of the overflow structure, the labyrinth spillway discharge capacity is affected by many factors including weir geometry and approach channel conditions [1] . A labyrinth weir is a linear weir that is “folded” in plan-view to increase the crest length for a given channel or spillway width [2] .
Optimizing the many geometric variables in the hydraulic design of a labyrinth weir can be challenging. For example, the sidewall angle (α), total crest length (Lc), crest shape, number of cycles (N), the configuration of the labyrinth cycles, and the orientation and placement of a labyrinth weir must all be determined. Furthermore, the geometry of a labyrinth weir causes complex 3-dimensional flow patterns that must be considered. The flow rate passing over the labyrinth is dependent on the crest length, which can be controlled by modifying the number of folds. The relationship between lengthand discharge is not linear, however, except for very small heads. As the water level above the labyrinth weir increases, four stages of nappe shape occur: fully aerated, partially aerated, transition and submerged. The thickness of nappe and depth of the tail water do not affect the discharge capacity of the labyrinth weir in the fully aerated flow condition. In this case, the labyrinth weir acts as a vertical cross section of the linear weir. As the water level above the labyrinth weir increases and the tail water rises, the nappe becomes partially aerated (adhering to the weir wall) and the discharge coefficient is reduced [3] [4] . During this phase, there may be alternating conditions of fully aerated and adhered nappe flow. The alternating nappe pressures between sub-atmospheric (negative) pressure and atmospheric pressure create vibrations, oscillations and noise. Although the negative pressures under water nappe increase the discharge capacity of the spillway, the associated vibration and resonance may negatively impact the safety of the structure.
The jet of water that passes over a weir is referred to as the nappe. Nappe aeration conditions for a variety of linear weirs have been previously investigated and documented [5] - [7] . The effects of water-air interaction should be considered in spillway design, as in many hydraulic structure designs [8] .
Schwartz [9] discussed theories behind the nappe vibration mechanism occurring on weirs, including the possible effects of edge tones, as well as the possible link between nappe oscillations and weir crest boundary layer conditions. Casperson [10] studied nappe oscillations occurring on fountains in New Zealand (weir flow conditions), deriving equations to model the position of the nappe during oscillation, and attributed the cause of instability to the Helmholtz effect [11] .
In addition to literature regarding the nappe vibration mechanism, several studies have focused on nappe vibration mitigation. Nappe vibration can be attributed to three different factors: instability of the nappe itself, fluctuation of air pressure behind the nappe, and the structure acting as a vibrating system [12] . One major focus of research regarding nappe vibration has been to develop a better understanding of countermeasures, such as in the case of the Avon Dam Spillway [13] .
At high heads, nappe instability may also require remedial action, depending on the corresponding noise levels and fluctuation frequency. Yildiz and Uzucek [4] and Hinchliff and Houston [14] both recommend nappe breakers to suppress nappe instability; the Flamingo spillway (Las Vegas, Nevada), for example, features nappe breakers.
Over the past 50 years, extensive research on the influence of geometric and hydraulic parameters on the hydraulic behavior of labyrinth weirs, particularly on the discharge capacity, has been completed. Taylor [15] presented initial studies on the behavior of labyrinth weirs and presented the hydraulic performance as it compares with that of sharp-crested weirs. Hay and Taylor [16] followed up on Taylor’s work and developed design criteria for labyrinth weirs. Basesd on their research findings, they suggested Equation (1) for the discharge coefficient of labyrinth weirs.
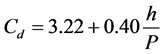 (1)
(1)
where Cd is the discharge coefficient; h is the depth of flow over the weir crest and P is the weir height.
Additional work by Darvas [17] utilized the results from physical model studies to expand on the theory and develop a family of curves to evaluate spillway performance. Extensive physical model studies were performed by Houston [18] to evaluate various labyrinth geometries and approach conditions. The US Bureau of Reclamation (USBR) tested a model of labyrinth spillway for Ute Dam and Hyrum Dam [18] [19] . They found that the discrepancy between their observations and those of Hay and Taylor [16] were caused by difference in head definition.
Lux [20] has also investigated model studies of the labyrinth weir and Equation (2) is his suggested equation for calculation of discharge over labyrinth weirs.
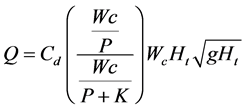 (2)
(2)
where Q is the discharge over labyrinth weir; Cd is the discharge coefficient; Ht is the total upstream head measured relative to the weir crest; Wc is the channel width and P is the weir height.
Magalhaes and Lorena [21] calculated discharge coefficient (Cd) of labyrinth weirs as function of L/w and Ht/P parameters. They defined discharge capacity of labyrinth weirs with Equation (3).
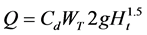 (3)
(3)
Tullis et al. [22] carried out extensive experimental work on the performance of the labyrinth weir. They proposed a flow equation for the labyrinth weir that is identical to the basic equation applicable to a linear weir, but with modification of the coefficient of discharge. They also presented experimental data of the variation of discharge coefficient of labyrinth weir with a head to weir height ratio (Ht/P) for side wall angles (α) of 6˚ to 18˚. Additional curves for weir side angles of 25˚ and 35˚ were obtained by extrapolation. Tullis et al. [23] extended this work by providing a dimensionless head-discharge relationship for submerged labyrinth weirs. Using a physical model of the labyrinth weir of Dog River Dam in Georgia, Savage et al. [24] showed that the method of Tullis et al. [22] produced a discharge error up to ±25%.
Labyrinth weirs are also used as side weirs to increase the outflowing discharge. Emiroglu et al. [25] carried out extensive experimental work on the performance of the labyrinth side weirs and presented coefficient of discharge curves in a simplified way as compared to previous investigators. Further work on triangular labyrinth side weirs was completed by Bilhan et al. [26] using Artificial Neural Network (ANN) techniques to calculate the discharge coefficient under critical flow conditions.
Khode et al. [27] carried out flume studies on trapezoidal labyrinth weirs for side wall angles 6˚, 8˚, 10˚, 16˚, 21˚, 26˚ and 30˚. Khode et al. [28] extended these studies for a wider range of flow conditions.
Carollo et al. [29] studied the outflow process from a sharp-crested triangular labyrinth weir. Applying dimensional analysis and the Π theorem, five dimensionless parameters were determined as important to the description of the outflow process. A dimensionless stage-discharge relation was developed.
Crookston and Tullis [30] published labyrinth weir design equations that are applicable to in-channel labyrinth weir applications in which the approach flow is oriented normal to the weir axis. Consequently, some uncertainty exists regarding the hydraulic performance of labyrinth weir configurations that deviate from the experimental conditions associated with the empirical determinations.
Crookston and Tullis [31] investigated the labyrinth weir nappe interference and identified labyrinth weir flow characteristics that decrease discharge efficiency, including local submergence. The authors presented parametric methods for quantifying nappe interference region size as a function of weir geometry (e.g., sidewall angle and crest shape) and flow conditions (e.g., headwater and nappe aeration).
Anderson and Tullis [32] investigated 9 laboratory-scale four-cycle PK weir configurations to develop a better understanding of the effects of PK weir geometry on discharge efficiency. The appropriateness of the recommended head-discharge equation specific to the recommended design was evaluated, and the relative head-discharge efficiency of trapezoidal labyrinth and PK weirs with respect to footprint restrictions and crest length were compared in this study.
Information regarding nappe aeration conditions (clinging, aerated, partially aerated, and drowned), nappe instability, and nappe vibrations for trapezoidal labyrinth weirs on a horizontal apron with quarter-and half-round crests (6˚ ≤ α ≤ 35˚) was presented by Crookston and Tullis [33] . In this study, hydraulic behaviors associated with nappe aeration conditions were documented to aid in labyrinth weir design, including design options directly related to nappe behavior (e.g., crest shape, crest roughness, vents, nappe breakers, notches, and staged cycles). The effect of artificial nappe aeration (vented nappe) on nappe behavior and discharge capacity was also evaluated, including recommended placement of nappe breakers.
While all these documented studies have provided significant insights to the behavior of labyrinth weirs under specific conditions, the general theory remains: the capacity of labyrinth weir is a function of the upstream total head, the effective crest length, and the coefficient of discharge. The discharge coefficient depends on the total head, weir height, thickness, crest shape, apex configuration, and angle of side wall. While viscosity and surface tension are also significant variables, their influence is limited at velocities of sufficient magnitude and by appropriate model geometries [5] .
The purpose of this study is to systematically investigate the discharge capacity of sharp-crested trapezoidal and circular labyrinth weir with and without nappe breaker, using a broad range of experiments, and considered together with the other effective dimensionless parameters.
2. Experimental Set-up and Experiments
Experiments on the discharge capacity and flow characteristics of the labyrinth weirs were carried out using a model located in the hydraulic laboratory of Firat University, Elazig, Turkey. The experimental set-up includes sump, pumping system, discharge tank, rectangular flume, digital flowmeter and labyrinth weir. Water is recirculated through 250 mm diameter of supply line using two 75 HP pumps. Water for experimental setup is taken from the supply line by means of a pipe with 150 mm diameter. The discharge was measured by means of a Siemens electromagnetic flow-meter installed in the supply line. Water was supplied to the main channel (2 m wide and 0.80 m height this channel length is 3.0 m) through a supply pipe from the sump (volume of 15 m3) with flow controlled by a gate valve (Figure 1). For damping the water surface waves and reducing turbulence, baffle wall and wood surface dampener is provided. In the experiments, the upstream elevation was built higher than the downstream elevation so that free flow conditions occur downstream of the weir. Sheet metal materials which have 4 mm thickness (t) were used for labyrinth weirs. The upstream apex angle of the nappe breakers was taken as 105˚ and downstream apex shape was manufactured as rounded. Labyrinth weirs designed as three- cycles. The nappe breakers have 130 mm high and 8 mm of thickness which were used in the experiments, the nappe breakers were placed on the middle of upstream and downstream apex for trapezoidal labyrinth weirs and they were placed on the middle of each circular cycle for the circular labyrinth weirs. Schematic view of trapezoidal and circular labyrinth weirs is given in Figure 2. Each labyrinth weir models with a sharp crested shape was tested with and without nappe breakers in the experiments (Examples shown in Figure 3).
To measure the nappe height, water depth was measured accurately using Mitutoyo digital point gauges (accurate to ±0.01 mm) just upstream of the weirs. Level measurements were taken at a distance from the weir equal to five times the nappe height. For flow rate measurements, Nortek brand acoustic three-axis velocimeter was used.
In the experiments, the weir heights were taken as 100 mm, 150 mm and 200 mm and apex width (A) was taken as 80 mm. Sharp-crested shapes is provided for all models. All experiments were performed according to free flow conditions.
The flow over labyrinth weir is three dimensional and does not readily fit into mathematical description and hence the discharge function is found through experimental studies and analysis. The crest coefficient depends on the total head, weir height, thickness, crest shape, apex configuration and angle of side wall. To simplify the analysis, the effect of viscosity and surface tension could be neglected by selecting model and velocity of sufficient magnitude. The discharge over labyrinth weir can be expressed as:
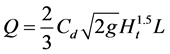 (4)
(4)
where Q is the discharge over a labyrinth weir; Cd is the discharge coefficient of the labyrinth weir; L is the effective length of labyrinth weir; Ht is the total head (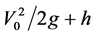 ) and g is the gravitational acceleration constant (Figure 4).
) and g is the gravitational acceleration constant (Figure 4).
Head over labyrinth weir was measured for different value of discharges in the range of 14.7 L/s to 136.9 L/s. In this range, the head over the labyrinth weir varied from 10 to 90 mm. The model of linear weir is also tested in the same flume for the purpose of comparison. In the experiments, the characteristics of different types of the weirs which are tested in the experiments are given in Table 1.
The objective of this research is to further the understanding related to the mechanisms that cause nappe vibration, document the occurrence conditions, and investigate mitigation techniques for trapezoidal and circular labyrinth weirs.
Figure 1. Experimental arrangement.
Figure 2. Schematic view of the trapezoidal and circular labyrinth weirs located on straight channel.


Figure 3. Experimental set-up for: (a) Trapezoidal labyrinth weir (b) Trapezoidal labyrinth weir with nappe breakers (c) Circular labyrinth weir (d) Circular labyrinth weir with nappe breakers.
Figure 4. Definition sketch for flow over a sharp crested weir.
Table 1. Physical model geometrics for weirs tested in the present study.
3. Experimental Results and Analysis
Experiments are carried out on six trapezoidal labyrinth weir models having side wall angles of 12˚, 15˚, 18˚, 23˚, 30˚ and 37˚, circular labyrinth weir models and a linear weir models having sharp crested shape similar to labyrinth weirs models. On all these models, head-discharge measurements are taken for weir height of P = 10, 15 and 20 cm. In addition, experiments were repeated by placing nappe breakers on all models of the labyrinth weirs. A total of 24 different configurations were examined in these experiments.
Discharge coefficient for labyrinth weirs was computed using equation (Equation (4)). Discharge coefficients of labyrinth side weirs have much higher values than the conventional weirs. The effect of crest shape on the discharge coefficient is very significant for the same channel width and crest length.
In this study, the nappe breakers installed on the crest spaced at a regular interval is a remedy used on prototype spillways to eliminate nappe oscillation. The nappe breakers create a break in the continuous lateral nappe profile, venting the confined air pocket (if one exists) behind the nappe to atmospheric pressure. Anderson, A.A. [5] used laboratory-scale physical models for nappe breakers in Utah State University. The results of this experimental study showed that adding more nappe breakers and shortening the spacing is most effective at disrupting the vibration. This, of course, is a general statement on what was observed on this model, and does not provide specific nappe breakers spacing design parameters for any given weir spillway.
From these experiments, the variation of Cd for trapezoidal labyrinth weirs with Ht/P is plotted for P = 10, 15 and 20 cm in Figure 5. The variation of Cd for trapezoidal labyrinth weirs with nappe breakers is plotted in Figure 6 and the variation of Cd for circular labyrinth weirs with and without nappe breakers is plotted together in Figure 7. It is noted that discharge coefficient for labyrinth weirs is computed using equation (Equation (4)). It is apparent from the results in Figure 5 and Figure 6 that discharge capacity of the labyrinth weirs is much higher than the conventional weirs. The primary reason for this is that the crest length of the labyrinth weir is much longer than that of the conventional weir. The test data showed that nappe breakers used with the circular labyrinth weirs reduced the discharge coefficient as by about 2% (Figure 7). Nappe breaker constitutes an impediment in the direction of flow and it decreases the length of the overflow. Therefore, discharge capacity of the labyrinth weir without breaker is more than that of the labyrinth weir with nappe breaker.
Figure 5. Variation of discharge coefficient (Cd) with head to weir height (Ht/P) for trapezoidal labyrinth weirs.
Figure 6. Variation of discharge coefficient (Cd) with head to weir height (Ht/P) for trapezoidal labyrinth weirs with nappe breakers.
Figure 7. Variation of discharge coefficient (Cd) with head to weir height (Ht/P) for circular labyrinth weirs with/without nappe breakers.
Also, the variation of discharge coefficient (Cd) with head to weir height (Ht/P) for trapezoidal labyrinth weirs (a = 37˚, L = 294 cm, N = 3, P = 10 - 15 - 20 cm) and circular labyrinth weirs (L = 294 cm, N = 3, P = 10 - 15 - 20 cm) which have the same crest length is plotted in Figure 8. The discharge capacity of trapezoidal labyrinth weirs according to the circular labyrinth weirs can be seen to be higher in Figure 8. The important effect of nappe breakers on discharge coefficient can be seen in the range from 0.2 to 0.6 of Ht/P. Similarly, to establish a relationship between Lc/w with Cd the observed data are plotted and shown in Figure 9.
To represent the data of the equation form, correlation analysis is carried out for the observed data for each model, separately. The 5th degree polynomial provides a reasonable fit between Cd and Ht/P. Thus, discharge coefficient (Cd) of sharp-crested labyrinth weir with and without nappe breaker is expressed as:
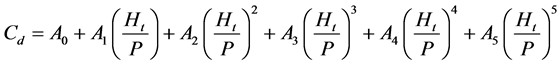 (5)
(5)
The values of Cd, A0 to A5, and R2 are shown in Tables 2-4.
According trapezoidal labyrinth weir test data in Figure 10, the nappe breakers reduced the discharge coefficient (Cd) depending on side wall angels (12˚, 15˚, 18˚, 23˚, 30˚, 37˚) in the range from 0.1 to 0.5 of Ht/P. The effect of nappe breakers on discharge coefficient is a negligible level for α = 12˚ in the range from 0.1 to 0.5 of Ht/P. Similarly, the test data showed that the nappe breakers which have 12˚, 15˚, 18˚, 23˚, 30˚, 37˚ side wall angles reduced the discharge coefficient by 3.50% to 3.80%. As shown in Figure 7, nappe breakers used on the circular labyrinth weirs reduced the discharge coefficient, but only slightly (∼2%).
The discharge coefficient values of labyrinth weir compared well with those of Woronora Dam, Boardman Dam, and Avon Dam. Moreover, the results of the present study compared well with those of Tullis et al. [22] , as shown in Figure 11. Although the data values are different, due to the variation in nappe shape and side wall angle for each study, the trends are similar to the findings of Tullis et al. [22] and prototype data.
4. Conclusions
Labyrinth weirs can pass large flows at comparatively low heads. The crest shape is one of the most important factors which affect the discharge capacity for labyrinth weirs. According to this experimental study, it has found that the trapezoidal labyrinth weirs are hydraulically more efficient than the circular labyrinth weirs and linear weirs from the perspective of ease of construction and the discharge capacity.
Variation of the nappe pressure between sub-atmospheric pressure and atmospheric pressure causes vibrations, oscillations and noise. Although the negative pressures under water nappe partially increase the discharge ca-
Figure 8. Variation of discharge coefficient (Cd) with head to weir height (Ht/P) for trapezoidal, circular labyrinth weirs and linear weir.

Figure 9. Variation of discharge coefficient (Cd) with Lc/w for trapezoidal labyrinth weirs (a) without nappe breakers; and (b) trapezoidal labyrinth weirs with nappe breakers.
Table 2. Coefficient of discharge per unit length of trapezoidal labyrinth weir.



Figure 10. Variation of discharge coefficient (Cd) with head to weir height (Ht/P) for trapezoidal labyrinth weirs with and without nappe breakers: (a) a = 12˚; (b) a = 15˚; (c) a = 18˚; (d) a = 23˚; (e) a = 30˚ and (f) a = 37˚.



Figure 11. Variation of discharge coefficient (Cd) with head to weir height (Ht/P) for present study compared to other findings: (a) Woronora Dam [17] ; (b) Boardman Dam [34] , (c) Avon Dam [17] ; (d)-(f) data from Tullis et al. [22] .
pacity of the labyrinth weirs, effects of vibration and resonance may cause problems that could threaten the safety of the structure.
Alleviation of these effects and to minimize the dynamic effects on structures can be possible with the nappe breakers which are placed on the labyrinth weirs. While it has been targeted to minimize these dynamic effects
Table 3. Coefficient of discharge per unit length of trapezoidal labyrinth weir with nappe breakers.
Table 4. Coefficient of discharge per unit length of circular labyrinth weirs with and without nappe breakers.
with nappe breakers which are placed on circular and trapezoidal labyrinth weirs, it also has been examined the effects on discharge coefficient in this experimental study. The values for coefficient of discharge can be suitably obtained from the design curves and the regression equation generated through this study for trapezoidal and circular labyrinth weirs with/without nappe breakers.
The values for discharge coefficient of trapezoidal labyrinth weirs with and without nappe breakers can be suitably obtained from the design curves and the regression equations generated through this study for α between 12˚ and 37˚.
For trapezoidal labyrinth weirs, with Ht/P in the range from 0.1 to 0.5, the nappe breakers reduced the discharge coefficient Cd by 0.5% - 4% depending on side wall angles (12˚, 15˚, 18˚, 23˚, 30˚, 37˚). The reduction in discharge coefficient for nappe breakers on circular labyrinth weir is about 2 %.
Of course, given unlimited width, greater efficiencies (discharge per head) will be obtained for a linear weir. However, the trapezoidal provides much greater weir length in confined space with only limited reductions in efficiency (reduction in Cd). The circular weir is the least efficient of those investigated.
The nappe breakers located on the weir crest have proven to be an effective countermeasure by several researchers, but specific spacing of nappe breakers for a weir of a given height and width has not been determined and would be a valuable focus of future research, along with further investigation of the aspect ratio of flow depth to nappe width conducive to nappe vibration. A better understanding of the causes and preventative measures of nappe vibration will aid engineers in the design of dam spillways structures.
Acknowledgements
Funding for this study was provided by the Scientific Research Project Department of Firat University in Turkey, Project No: 1610. The authors gratefully acknowledge the assistance of Mr. Javad Roostaei in the preparation of Figures and Tables for this manuscript.
Cite this paper
Omer Bilhan,M. Emin Emiroglu,Carol J. Miller, (2016) Experimental Investigation of Discharge Capacity of Labyrinth Weirs with and without Nappe Breakers. World Journal of Mechanics,06,207-221. doi: 10.4236/wjm.2016.67017
References
- 1. Yildiz, D. and Uzucek, E. (1993) Labirent Dolusavaklarin Projelendirilme Kriterleri. Devlet SuIsleri Teknik Arastirma Kaliteve Kontrol Dairesi Baskanligi. Yayin No: HI-862 Ankara, Turkey.
- 2. Crookston, B.M. and Tullis, B.P. (2012) Labyrinth Weirs: Nappe Interference and Local Submergence. Journal of Irrigation and Drainage Engineering, ASCE, 138, 757-765.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000466 - 3. Tsang, C. (1987) Hydraulic and Aeration Performance of Labyrinth Weirs. PhD Dissertation, University of London, UK.
- 4. Yildiz, D. and Uzucek, E. (1996) Modeling the Performance of Labyrinth Spillways. The International Journal on Hydropower and Dams, 3, 71-76.
- 5. Anderson, A.A. (2014) Causes and Countermeasures for Nappe Oscillation: An Experimental Approach. All Graduate Theses and Dissertations, Utah State University, Logan, Paper 3296.
- 6. Chow, V.T. (1959) Open-Channel Hydraulics. McGraw-Hill, New York.
- 7. Kandaswamy, P. and Rouse, H. (1957) Characteristics of Flow over Terminal Weirs and Sills. Journal of Hydraulics Division, 83, 1-13.
- 8. Falvey, H. (1980) Chapter 2. Practical Experiences with Flow-Induced Vibrations. In: Naudascher, E. and Rockwell, D., Eds., Springer-Verlag, Berlin, Heidelberg, New York, 386-398.
http://dx.doi.org/10.1007/978-3-642-81528-7_42 - 9. Schwartz, H.I. (1966) Edgetones and Nappe Oscillation. Journal of Acoustical Society of America, 39, 579-582.
http://dx.doi.org/10.1121/1.1909930 - 10. Casperson, L.W. (1991) Fluttering Fountains. Journal of Sound and Vibration, 162, 251-262.
http://dx.doi.org/10.1006/jsvi.1993.1117 - 11. Von Helmholtz, H. (1868) über Discontinuierliche Flüssigkeits-Bewegungen [On the Discontinuous Movements of Fluids]. Monatsberichte der Königlichen Preussische Akademie der Wissenschaftenzu Berlin [Monthly Reports of the Royal Prussian Academy of Philosophy in Berlin], 215-228.
- 12. Sato, Y., Miura, S., Morii, S. and Ohkubo, S. (2007) Behavior of a Falling Water Sheet. Journal of Environment and Engineering, 2, 394-406.
http://dx.doi.org/10.1299/jee.2.394 - 13. Metropolitan Water, Sewerage and Drainage Board (1980) Investigation into Spillway Discharge Noise at Avon Dam. ANCOLD Bulletin No. 57, Sydney, 31-36.
- 14. Hinchliff, D. and Houston, K. (1984) Hydraulic Design and Application of Labyrinth Spillways. Proceedings of 4th Annual USCOLD Lecture, Dam Safety and Rehabilitation, Bureau of Reclamation, US Department of the Interior, Washington DC.
- 15. Taylor, G. (1968) The Performance of Labyrinth Weirs. PhD Thesis, University of Nottingham, UK.
- 16. Hay, N. and Taylor, G. (1970) Performance and Design of Labyrinth Weir. Journal of Hydraulic Engineering (ASCE), 96, 2337-2357.
- 17. Darvas, L. (1971) Discussion of Performance and Design of Labyrinth Weirs, by Hay and Taylor. Journal of Hydraulic Engineering (ASCE), 97, 1246-1251.
- 18. Houston, K. (1982) Hydraulic Model Study of Ute Dam Labyrinth Spillway. Report No. GR-82-7, US Bureau of Reclamation, Denver.
- 19. Houston, K. (1983) Hydraulic Model Study of Hyrum Dam Auxiliary Labyrinth Spillway. Report No. GR-82-13, US Bureau of Reclamation, Denver.
- 20. Lux, F. (1989) Design and Application of Labyrinth Weirs. Design of Hydraulic Structures 89, Balkema, Rotterdam.
- 21. Magalhaes, A. and Lorena, M. (1989) Hydraulic Design of Labyrinth Weirs. Report No. 736, National Laboratory of Civil Engineering, Lisbon, Portugal.
- 22. Tullis, B.P., Amanian, N. and Waldron, D. (1995) Design of Labyrinth Weir Spillways. Journal of Hydraulic Engineering (ASCE), 121, 247-255.
http://dx.doi.org/10.1061/(ASCE)0733-9429(1995)121:3(247) - 23. Tullis, B.P., Young, J. and Chandler, M. (2007) Head-Discharge Relationships for Submerged Labyrinth Weirs. Journal of Hydraulic Engineering (ASCE), 133, 248-254.
http://dx.doi.org/10.1061/(ASCE)0733-9429(2007)133:3(248) - 24. Savage, B., Frizell, K. and Crowder, J. (2004) Brains versus Brawn: The Changing World of Hydraulic Model Studies. ASDSO 2004 Annual Conference Proceeding, Association of State Dam Safety Officials (ASDSO).
https://www.flow3d.com/wp-content/uploads/2014/08/Brains-versus-Brawn-The-Changing-World-of-Hydraulic-Model-Studies.pdf - 25. Emiroglu, M.E., Kaya, N. and Agaccioglu, H. (2010) Discharge Capacity of Labyrinth Side Weir Located On a Straight Channel. Journal of Irrigation and Drainage Engineering (ASCE), 136, 37-46.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000112 - 26. Bilhan, O., Emiroglu, M.E. and Kisi, O. (2011) Use of Artificial Neural Networks for Prediction of Discharge Coefficient of Triangular Labyrinth Side Weir in Curved Channels. Journal of Advances in Engineering Software, 42, 208-214.
http://dx.doi.org/10.1016/j.advengsoft.2011.02.006 - 27. Khode, B.V., Tembhurkar, A., Porey, P. and Ingle, R. (2011) Determination of Crest Coefficient for Flow over Trapezoidal Labyrinth Weir. World Applied Sciences Journal, 12, 324-329,
- 28. Khode, B.V., Tembhurkar, A., Porey, P. and Ingle, R. (2012) Experimental Studies on Flow over Labyrinth Weir. Journal of Irrigation and Drainage Engineering (ASCE), 138, 548-552.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000336 - 29. Carollo, F., Ferro, V. and Pampalone, V. (2012) Experimental Investigation of the Outflow Process over a Triangular Labyrinth-Weir. Journal of Irrigation and Drainage Engineering (ASCE), 138, 73-79.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000366 - 30. Crookston, B.M. and Tullis, B.P. (2012) Arced Labyrinth Weirs. Journal of Hydraulic Engineering (ASCE), 138, 555-562.
http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000553 - 31. Crookston, B.M. and Tullis, B.P. (2012b) Discharge Efficiency of Reservoir-Application Specific Labyrinth Weirs. Journal of Irrigation and Drainage Engineering (ASCE), 138, 564-568.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000451 - 32. Anderson, R.M. and Tullis, B.P. (2013) Piano Key Hydraulics and Labyrinth Weir Comparisons. Journal of Irrigation and Drainage Engineering (ASCE), 139, 246-253.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000530 - 33. Crookston, B.M. and Tullis, B.P. (2013) Hydraulic Design and Analysis of Labyrinth Weirs. II: Nappe Aeration, Instability, and Vibration. Journal of Irrigation and Drainage Engineering (ASCE), 139, 371-377.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000553 - 34. Baab, A.F. (1976) Hydraulic Model Study of the Boardman Reservoir Spillway, R.L. Albrook Hydraulics Laboratory, Washington State University, Pullman, Wash.
Notation
NOTES
*Corresponding author.










