World Journal of Mechanics
Vol.06 No.02(2016), Article ID:63603,5 pages
10.4236/wjm.2016.62003
On the Potential Application of the Wrinkled SiGe/SiGe Nanofilms
Alexander I. Fedorchenko1,2*, Henry H. Cheng3, Wei-Chih Wang4
1Institute of Thermomechanics of CAS, Prague, Czech Republic
2S. S. Kutateladze Institute of Thermophysics, Siberian Branch of RAS, Novosibirsk, Russia
3Center for Condensed Matter Sciences, National Taiwan University, Taiwan
4Department of Mechanical Engineering, University of Washington, Seattle, WA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 December 2015; accepted 19 February 2016; published 22 February 2016
ABSTRACT
Terahertz radiation (THzR) consists of electromagnetic waves within the band of frequencies from 0.3 to 3 terahertz with the wavelengths of radiation in the range from 0.1 mm to 1 mm, respectively. The technology for generating and manipulating THzR is still in its initial stage. Herein, we demonstrate that the wrinkled Si1−xGex/Si1−yGey films can be used as radiation sources, which emit electromagnetic waves (EMW) in a very wide range of the frequencies including the terahertz band from 0.3 to 3 THz and far IR from 3 THz to 20 THz. These findings provide the theoretical foundation for the wrinkled nanofilm radiation emission and may allow, to some extent, to fill the terahertz gap.
Keywords:
Wrinkled SiGe Nanofilms, Terahertz Radiation, Terahertz Gap

1. Introduction
Terahertz radiation (THzR) consists of electromagnetic waves within the band of frequencies from 0.3 to 3 terahertz with the wavelengths of radiation in the range from 1 mm to 0.1 mm, respectively. THzR occupies a middle ground between microwaves and infrared light waves. The technology for generating and manipulating THzR is still in its initial stage, and is the subject of the intensive researches [1] - [3] . This lack of technology is called the terahertz gap with frequencies from 0.1 to 10 THz (wavelengths from 3 mm to 30 µm) [4] [5] . It represents the region in the electromagnetic spectrum that the frequency of electromagnetic radiation becomes too high to be measured by digitally counting cycles using electronic counters. In this frequency range, the generation and modulation of coherent electromagnetic signals ceases to be possible by the conventional electronic devices used to generate radio waves and microwaves, and requires new devices and techniques.
The theory of the radiation emission from the wrinkled pattern [6] is based on two important assumptions: 1) the sample should be quite extended and strictly periodic over the entire length and 2) the carriers should travel along the wrinkled free edge. As can be seen from Figure 1 in Fedorchenko et al. [7] , the wrinkled pattern does not satisfy the first assumption. Moreover, at that time the technology does not allow to obtain samples with preset geometrical parameters, such as the wrinkle period. Recent advances in the theory [8] and technology of production of strictly periodic wrinkled SiGe nanofilms [7] [9] -[11] provide the theoretical foundation for the wrinkled nanofilm radiation emission and may allow, to some extent, to fill the terahertz gap.
The main finding of this work is that with proper wrinkled nanofilms the electromagnetic waves within terahertz band or far IR can be generated.
2. Mechanism of Radiation
Conventionally, optical emission from semiconductors is via the conduction-to-valence band optical transitions. The emission intensity of IV-IV compounds is relatively weak as compared to III-V compounds owing to the indirectness of the energy band in the momentum space. Very recently, a novel radiation emission mechanism from wrinkled Si1−xGex/Si1−yGey nanofilms has begun to be explored [6] . The emission mechanism is based on the change of acceleration of carriers, when they travel along the sinusoidal trajectory in wrinkled Si1−xGex/ Si1−yGey nanofilms. This manner is analogous to synchrotron radiation with undulators, or a free-electron laser.
The improvement of technology for production of the wrinkled SiGe/SiGe nanofilms allows us to produce strictly periodic nanostructures with predetermined geometrical properties, such as the wrinkled pattern length and the wrinkle period (see Figure 1).
Following [7] [9] , the characteristics of the wrinkled nanostructure were described as follows. The structure consists of two thin layers of Si1−xGex/Si1−yGey with different Ge compositions deposited on a Si buffer layer. Both layers are p-type doped and are initially strained because of the lattice mismatch between the Si buffer layer and the bilayer. By removing the Si buffer layer using the standard semiconductor process of selective etching, the bilayer thin film is debonded, resulting in a freestanding film. The freestanding film relaxes through bending and stretching and eventually reaches its equilibrium state, forming a wrinkled pattern. A typical AFM image of the wrinkled pattern and its schematic plot are depicted in Figure 2 and Figure 3, respectively.
The freestanding bilayer film has air between the pattern and the silicon substrate. A detailed description of the fabrication process and formation mechanism of the pattern is reported in [7] [9] . The morphology of the wrinkled pattern is characterized by a) the displacement in the growth direction z(x, y), and b) periodicity of the pattern (Lw). The displacement can be expressed as a function of Lw as z(x, y) = Ag(y/h) sin kx, where k = 2π/Lw is the wrinkle wave number, A and h are the wrinkle amplitude and lateral etching depth. Note that g(1) = 1 at the free edge (at y = h) and g(1) = 0 in the bonded area.
Figure 1. Array of SiGe wrinkled nanofilms.
Figure 2. A typical AFM image of the wrinkled pattern.
Figure 3. Schematic plot of the wrinkled pattern. Holes (solid circle) travel through a sinusoidal trajectory when a voltage is applied along (in x direction) the wrinkled pattern.
The carriers (holes in our case) in the bilayer film are initially confined within a triangular potential that is formed at the Si1−xGex/Si1−yGey interface, confined like a two-dimensional hole gas [8] . By placing a metal contact at both ends of the wrinkled pattern, holes travel through the wrinkles when a voltage is applied across the contacts as illustrated in Figure 3. To support the theoretical results of the paper [6] , important outcomes of Chang et al. [8] pertinent to the valence band profile in the wrinkled SiGe/SiGe nanofilm should be mentioned.
Namely, their findings show that the strain in the SiGe layer lifts the degeneracy of the valence band spitting into heavy and light hole states.
From an analysis of the energy profile of the structure using the multi-band k×p approximation it is found that, the energy minimum lies along the wrinkled edge with heavy state being the lowest. The energy minimum lies along the wrinkled free edge and remains one-dimensional. Thus the majority of the carriers (holes) travel along the one-dimensional trajectory at the wrinkled free edge.
As the energy splitting of the heavy-light holes state at the edge (»100 meV) is much larger than the phonon energy (»55 meV), thus the inter valley scattering is weak in this case.
3. Results and Discussion
Omitting the intermediate mathematical calculations, which can be found in the paper [6] , the final results are of the form:
 (1)
(1)
where c is the speed of light in vacuum, Vd = μE is a constant average velocity of holes under the influence of applied electric field E, μ is the hole mobility whose value depends on the composition of the samples, f and l are the frequency and wavelength of the emitted EMW, respectively.
Equation (1) shows that the radiated frequency depends mostly on two factors: a) the periodicity of the wrinkled pattern as Lw−1 and b) the hole average velocity Vd. With respect to the former factor, as has been shown in [7] [9] , layers with various Lw can be fabricated. Both the wavelength and amplitude of wrinkles increase with the depth of etching as h0.62 [7] [9] [10] . Further, the hole velocity is proportional to the magnitude of the applied electric field E. The radiated frequency for various Lw is calculated as a function of electric field ranging from 1 kV/cm to 100 kV/cm. The mobility of the heavy holes is set to 1400 cm2/V・s, which was deduced from the average value of the bilayer film of Si0.51Ge0.49/Si0.82Ge0.18 reported in [12] , and the mobility of each layer is linearly extrapolated from the bulk values of Si and Ge.
The results of calculations are presented in Figure 4. The spectrum covers a wide range from 0.01 to 100 THz. For large Lw (³1 µm), the device emits long wavelengths on the centimeter scale. As Lw decreases, which can be achieved by reducing the lateral etching depth, the emitted wavelength becomes shorter. For Lw = 0.1 µm the radiation falls into the terahertz band when the electric field changes from 2 kV/cm to 20 kV/cm. For Lw £ 0.1 µm, the emitted wavelengths are shifted into the infrared region and even reach the visible one.
As shown in [6] , the radiated power (P) for a single hole following the wrinkled trajectory reads
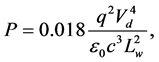 (2)
(2)
where q = 1.602 ´ 10−19 C is the carrier charge, and ε0 = 8.854 ´ 10−12 F/m is the dielectric constant. Equation (2) shows that the radiation power is inverse proportional to the periodicity of the wrinkled pattern as Lw−2 and depends strongly on the hole velocity as fourth power. This suggests that the width of the power spectrum is characterized by the statistical distribution of the hole velocity, skewing toward higher frequencies related to higher velocities.
The estimation given in [6] shows that for the conventional p-MOS device on the micron scale operated at high electrical field (a saturation velocity Vd = 107 cm/s, current of 1 mA, and Lw = 0.1 mm) a reasonable power is of sub-milliwatts. This demonstrates that the proposed nanostructure can be used as a tangible optical emitter at the infrared region and, in particular, in the terahertz band. Note that, by reducing periodicity of the wrinkled nanostructure, not only the radiated frequency shifts toward the visible region as shown in Figure 4, but the radiation power also increases.
4. Concluding Remarks
This study shows that the wrinkled Si1−xGex/Si1−yGey nanostructure could be potentially used as a source of terahertz radiation. The emission of the wrinkled SiGe/SiGe nanostructure can cover a wide spectrum from visible to far IR with radiation power levels of the order of submilliwats.
The mechanism of radiation emission is not related to the indirectness of the energy band and the bandgap of SiGe because the radiation emission depends only on the velocity of holes under an applied field and not on the
Figure 4. Emission spectra for different wrinkle periodicities. Dashed lines highlight the terahertz band.
conduction-to-valence transitions. This mechanism can help remove the main obstacle (indirectness in the energy band) in the use of group IV compounds as emission sources. For a wrinkled nanostructure with a fixed periodicity, the ability to tune the radiated frequency according to the velocity of holes implies that it can radiate light at different frequencies by changing the applied voltage. Thus, the proposed nanostructure offers a practical advantage over the conventional optical emitters that emit light with only a single frequency corresponding to the bandgap (the energy difference between the top of the valence band and the bottom of the conduction band).
Acknowledgements
This research has been supported by Institute of Thermomechanics of AS CR, project no. 902137.
Cite this paper
Alexander I.Fedorchenko,Henry H.Cheng,Wei-ChihWang,11, (2016) On the Potential Application of the Wrinkled SiGe/SiGe Nanofilms. World Journal of Mechanics,06,19-23. doi: 10.4236/wjm.2016.62003
References
- 1. Chamberlain, J.M. (2004) Where Optics Meets Electronics: Recent Progress in Decreasing the Terahertz Gap. Philosophical Transactions Royal Society of London A, 362, 199-414.
http://dx.doi.org/10.1098/rsta.2003.1312 - 2. Hu, Q. (2008) Terahertz Quantum Cascade Lasers and Real-Time T-Rays Imaging at Video Rate. International Journal of High Speed Electronics and Systems, 18, 983-992.
http://dx.doi.org/10.1142/S012915640800593X - 3. Scalari, G., Walther, C., Fischer, M., Terazzi, R., Beere, H., Ritchie, D. and Faist, J. (2009) THz and Sub-THz Quantum Cascade Lasers. Laser & Photonics Review, 3, 45-66.
http://dx.doi.org/10.1002/lpor.200810030 - 4. Kleiner, R. (2007) Filling the Terahertz Gap. Science, 23, 1254-1255. http://dx.doi.org/10.1126/science.1151373
- 5. Sirtori, C. (2002) Applied Physics: Bridge for the Terahertz Gap. Nature, 417, 132-133.
http://dx.doi.org/10.1038/417132b - 6. Fedorchenko, A.I., Cheng, H.-H., Sun, G. and Soref, R.A. (2010) Radiation Emission from Wrinkled SiGe/SiGe Nanostructure. Applied Physics Letters, 96, 119104.
http://dx.doi.org/10.1063/1.3360881 - 7. Fedorchenko, A.I., Cheng, H.-H., Mashanov, V.I. and Wang, A.-B. (2005) Wrinkling of a Debonded Initially Compressed Si1–xGex Film. Journal of Mechanics, 21, 131-135.
http://dx.doi.org/10.1017/S1727719100000563 - 8. Chang, G.-E., Wu, K.Y., Cheng, H.H., Sun, G. and Soref, R.A. (2012) Transformation of a Two-Dimensional to One-Dimensional Energy Profile on a Spatially Deformed Si0.82Ge0.18/Si0.51Ge0.49 Wrinkled Heterostructures. Journal Applied Physics 111, 104321.
http://dx.doi.org/10.1063/1.4723001 - 9. Fedorchenko, A.I., Wang, A.-B., Mashanov, V.I., Huang, W.-P. and Cheng, H.-H. (2006) Strain-Induced Wrinkling on SiGe Free Standing Film. Applied Physics Letters, 89, 043119.
http://dx.doi.org/10.1063/1.2236299 - 10. Cendula, P., Kiravittaya, S.F.M., Deneke, Ch. and Schmidt, O.G. (2009) Bending and Wrinkling as Competing Relaxation Pathways for Strained Free-Hanging Films. Physical Review B, 79, 085429.
http://dx.doi.org/10.1103/PhysRevB.79.085429 - 11. Huang, M.H., Cavallo, F., Liu, F. and Lagally, M.G. (2011) Nanomechanical Architecture of Semiconductor Nanomembranes. Nanoscale, 3, 96-120.
http://dx.doi.org/10.1039/C0NR00648C - 12. Huang, W.-P., Cheng, H.-H., Fedorchenko, A.I. and Wang, A.-B. (2007) Strain on Wrinkled Bilayer Thin Film. Applied Physics Letters, 91, 053103.
http://dx.doi.org/10.1063/1.2767204
NOTES
*Corresponding author.






