World Journal of Mechanics
Vol.05 No.12(2015), Article ID:61819,14 pages
10.4236/wjm.2015.512022
Magnetic Field and Thermal Radiation Effect on Heat and Mass Transfer of Air Flow near a Moving Infinite Plate with a Constant Heat Sink
S. M. Arifuzzaman1*, Sajal Kumar Dhali2, Md. Abul Kalam Azad1, Bibhuti Roy1
1Mathematics Discipline, Khulna University, Khulna, Bangladesh
2Computer Science and Engineering Discipline, Khulna University, Khulna, Bangladesh

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 3 November 2015; accepted 7 December 2015; published 10 December 2015

ABSTRACT
Analytical investigation on a combined heat and mass transfer of air flow near a continuously moving infinite plate with a constant heat sink is performed in the presence of a uniform magnetic field. To observe the thermal radiation and Soret effect on the flow, thermal radiation and thermal diffusion term are added in energy and concentration equations. A flow of model is established by employing the well known boundary layer approximations. In order to obtain non-dimensional system of equations, a similarity transformation is applied on the flow model. Perturbation technique is used as main tool for the analytical approach. The numerical values of flow variables are computed by a FORTRAN program. The obtain numerical values of fluid velocity, temperature and species concentration are drawn for the different values of various parameters. To observe the effects of various parameters on the flow variables, the results are discussed in detailed with the help of graph.
Keywords:
Viscous Fluid, MHD, Thermal Radiation, Heat Sink, Chemical Reaction, Soret Effects

1. Introduction
Fluid dynamics is the science which is concerned with the study of motion of fluids or that of bodies in contract of fluids. Fluids are classified as liquids and gases. The former are mot sensibly compressible expect under the action heavy forces whereas the latter are easily compressible and expand to fill any closed space. The heat transfer processes are of great interest in power engineering, metallurgy, astrophysics and geophysics. The processes of mass transfer have of great interest in the production of materials in order to obtain the desired properties of a substance. Chemical reactions including combustion processes are often decisively determined by the mass transfer. The combined heat and mass transfer occur due to buoyancy forces caused by temperature difference and concentration difference. A natural convective heat transfer flow of fluid was first studied by Finston (1956) [1] . Sparrow and Gregg (1958) computed a similar solution for laminar free convection from a non-isothermal vertical plate [2] . A Finite difference solution of transient free convective flow over an isothermal plate was obtained by Soundalgekar and Ganesan (1981) [3] . A numerical study on the natural convective cooling problem of a vertical plate was completed by Camargo et al. (1996) [4] . Chemical reactions including combustion processes are often decisively determined by the mass transfer. Callahan and Marner (1976) studied a free convective unsteady flow with mass transfer past a semi-infinite plate [5] . An investigation on free convective unsteady flow with mass transfer past an infinite vertical porous plate with constant suction was completed by Soundalgekar and Wavre (1977) [6] . Soundalgekar and Ganesan (1980) observed that Transient free convection flow on a semi-infinite vertical plate with mass transfer [7] .
Combined heat and mass transfer problems (Jaluria; 1980) are of importance in many processes and have therefore received a considerable amount of attention. In many mass transfer processes, heat transfer considerations arise owing to chemical reaction and are often due to nature of the process [8] . In processes such as drying, evaporation at the surface water body, energy transfer in a wet cooling tower and flow in desert cooler, heat and mass transfer occur simultaneously. The combined heat and mass transfer flows play a special role in power engineering, metallurgy, condensation, evaporation and rectification of a fluid. In the separation processes as drying of solid materials, distillation, extraction and absorption; the combined heat and mass transfer occur due to buoyancy forces caused by temperature difference and concentration difference. Pera and Gebhart (1971) was the first author to study the natural convective heat and mass transfer problem [9] - [14] . Hady, Mohamed and El Shehabey, (2013) focused on the effects of heat source/sink, viscous dissipation, radiation and work done by deformation on flow and heat transfer of a viscoelastic fluid over a nonlinear stretching sheet [15] . Viskanta and Grosh (1962) considered the thermal radiation effects on the boundary layer flow and heat transfer over a wedge in an absorbing and emitting media [16] . Bestman (1990) observed the boundary-layer flow past a semi-infinite heated porous plate for a two-component plasma [17] . Sattar and Alam (1994) considered the thermal-diffusion as well as transpiration effects on MHD free convection and mass transfer flow past an accelerated vertical porous plate [18] .
2. Analysis and Solution
2.1. Mathematical Flow
A mixed convective heat and mass transfer unsteady flow of air near an infinite vertical plate is considered here. The flow is assumed to be in the x-direction, which is chosen along the plate in upward direction and y-axis is normal to it. Initially, it is considered that the plate as well as the fluid particle is at rest at the same temperature 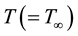 and the same species concentration level
and the same species concentration level 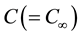 at all points. Where,
at all points. Where, 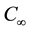 and
and 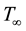 are fluid concentration and temperature species of uniform flow respectively. It also assumed that the plate and the fluid particles outside the boundary layer move with a uniform velocity
are fluid concentration and temperature species of uniform flow respectively. It also assumed that the plate and the fluid particles outside the boundary layer move with a uniform velocity 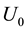 as well as a magnetic field B of uniform strength is applied normal to the flow region. To realize the model of boundary layer phenomena, we can draw the configuration of the model. The suitable physical configuration with co-ordinate systems is shown in Figure 1.
as well as a magnetic field B of uniform strength is applied normal to the flow region. To realize the model of boundary layer phenomena, we can draw the configuration of the model. The suitable physical configuration with co-ordinate systems is shown in Figure 1.
The unsteady two dimensional problems are governed by the following system of coupled non-linear partial differential equations.
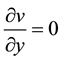 (1)
(1)
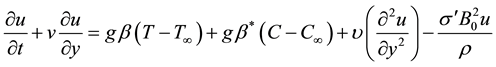 (2)
(2)
Figure 1. Physical configuration with co-ordinate system.
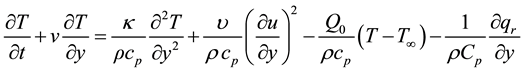 (3)
(3)
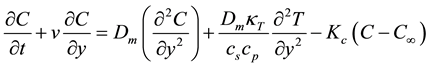 (4)
(4)
boundary conditions,
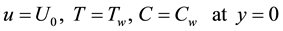
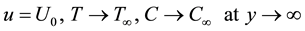
where,  be the Cartesian coordinate;
be the Cartesian coordinate; 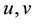 are velocity components, g is the local acceleration due to gravity,
are velocity components, g is the local acceleration due to gravity, 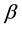 is the is the thermal expansion coefficient,
is the is the thermal expansion coefficient, 










Where, 






2.2. Mathematical Formulation
In order to obtain similar solutions we introduce a similarity parameter 
Such that 
Here, the constant 
We consider the following dimensionless variables,
Then we get,



where, Grashof number, 









Hence following the works of Sattar and Alam (1994) [18] one can try a class of solutions of the Equations (6), (7) and (8) by assuming that,

Now integrating (9) we obtain

where the constant of integration is determined through the condition that 





where, 
The dimensionless similar equations,



Non-dimensional appropriate boundary conditions,
2.3. Mathematical Analysis
Since the solution is sought for the large suction farther transformation can be made as,
Model with small quantity,
where,
Appropriate boundary conditions,
2.4. Solution
Now, for the large suction





The first order equations,

with the boundary conditions,
The second order equations,

with the boundary conditions,
Also the third order equations,

with the boundary conditions,
From Equation (17) we get first order solutions,
From Equation (18) we get second order solutions,
From Equation (19) we get third order solutions,
and
From the Equation (14), (15) and (16) we have series for the solution. Putting the equations of first, second and third order solution in the Equations (14), (15) and (16), we get the values of F, H and G. Substituting the values of F, H and G to the equations


The fluid velocity equation,
The fluid temperature equation,
The fluid concentration equation,
3. Results and Discussion
To discuss the results of the problem, the analytical solutions are obtained by using the perturbation technique. In order to analyze the physical situation of the model, we have computed the numerical values of the flow variables for different values of dimensionless normal velocity










In Figure 2 velocity profiles increase with the increase of heat absorption parameter









Figure 2. Velocity profiles for different values of 








Figure 3. Velocity profiles for different values of 







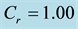
Figure 4. Velocity profiles for different values of 








Figure 5. Velocity profiles for different values of 








Figure 6. Temperature profiles for different values of 








Figure 7. Temperature profiles for different values of 









Figure 8. Temperature profiles for different values of 








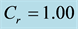
Figure 9. Concentration profiles for different values of 









Figure 10. Concentration profiles for different values of 





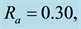



Figure 11. Concentration profiles for different values of 








Figure 12. Concentration profiles for different values of 







4. Conclusions
The analytic solutions o for MHD flow of a viscous fluid near a moving infinite plate with thermal radiation, heat sink, chemical reaction, Soret is analyzed. The results are presented graphically with various parameters. Form the graphical representation, we have the following observations:
・ Velocity and temperature profiles decrease with the increase of heat absorption parameter
・ Velocity profiles increase with the increase of magnetic force parameter M.
・ Velocity and temperature profiles decrease with the increase of radiation parameter 

・ Concentration profiles increase near the plate and away from the plate remain unchanged with the increase of Soret number
・ Concentration profiles decrease near the plate and away from the plate remain unchanged with the increase of chemical reaction parameter
Cite this paper
S. M.Arifuzzaman,Sajal KumarDhali,Md. Abul KalamAzad,BibhutiRoy, (2015) Magnetic Field and Thermal Radiation Effect on Heat and Mass Transfer of Air Flow near a Moving Infinite Plate with a Constant Heat Sink. World Journal of Mechanics,05,235-248. doi: 10.4236/wjm.2015.512022
References
- 1. Finston, M. (1956) Free Convection past a Vertical Plate. Journal of Applied Mathematical Physics (ZAMP), 7, 527-529.
- 2. Sparrow, E.M. and Gregg, J.L. (1958) Similar Solutions for Free Convection from a Non Isothermal Vertical Plate. ASME Journal of Heat Transfer, 80, 379-386.
- 3. Soundalgekar, V.M. and Ganesan, P. (1981) Finite-Differential Analysis of Transient Free Convection with Mass Transfer on an Isothermal Vertical Plate. International Journal of Engineering Science, 19, 757-770.
http://dx.doi.org/10.1016/0020-7225(81)90109-9 - 4. Camargo, R., Luna, E. and Trevino, C. (1996) Numerical Study of the Natural Convective Cooling of a Vertical Plate. International Journal of Heat and Mass Transfer, 19, 89-95.
http://dx.doi.org/10.1007/s002310050096 - 5. Callahan, G.D. and Marner, W.J. (1976) Transient Free Convection with Mass Transfer on an Isothermal Vertical Flat Plate. International Journal of Heat and Mass Transfer, 19, 165-174.
http://dx.doi.org/10.1016/0017-9310(76)90109-5 - 6. Soundalgekar, V.M. and Wavre, P.D. (1977) Unsteady Free Convection Flow past an Infinite Vertical Plate with Constant Suction and Mass Transfer. International Journal of Heat Mass Transfer, 20, 1363-1373.
http://dx.doi.org/10.1016/0017-9310(77)90033-3 - 7. Soundalgekar, V.M. and Ganesan, P. (1980) Transient Free Convective Flow past a Semi-Infinite Vertical Plate with Mass Transfer. Journal of Energy, Heat and Mass Transfer, 2, 83.
- 8. Jaluria, Y. (1980) Natural Convection Heat and Mass Transfer. Pergamon Press, Oxford.
- 9. Gebhart, B. and Pera, L. (1971) The Nature of Vertical Natural Convection Flows Resulting from the Combined Buoyancy Effect of Thermal and Mass Diffusion. International Journal of Heat Mass Transfer, 14, 2025-2050.
http://dx.doi.org/10.1016/0017-9310(71)90026-3 - 10. Singh, A.K., Singh, A.K. and Singh, N.P. (2003) Heat and Mass Transfer in MHD Flow of a Viscous Fluid past a Vertical Plate under Oscillatory Suction Velocity. Indian Journal of Pure and Applied Mathematics, 34, 429.
- 11. Chamka, A. and Khaled, A.R.A. (2001) Simultaneously Heat and Mass Transfer in Free Convection. Industrial Engineering Chemical, 49, 961-968.
- 12. Haque, M.M. and Sarder, U.K. (2015) Thermal Diffusion Effect on Convective Heat and Mass Transfer of High Speed MHD Flow over a Stretching Sheet. Journal of Scientific Research and Reports, 8, 1-14.
http://dx.doi.org/10.9734/jsrr/2015/18075 - 13. Anuradha, S. and Priyadharshini P. (2014) Heat and Mass Transfer on Unsteady MHD Free Convective Flow pass a Semi-Infinite Vertical Plate with Soret Effect. The International Journal of Science & Technoledge, 2, 328-337.
- 14. Bhattacharyya, K. and Layek, G.C. (2011) Effects of Suction/Blowing on Steady Boundary Layer Stagnation-Point Flow and Heat Transfer towards a Shrinking Sheet with Thermal Radiation. International Journal of Heat Mass Transfer, 54, 302-307.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.09.043 - 15. Hady, F.M., Mohamed, R.A. and ElShehabey, H.M. (2013) Thermal Radiation, Heat Source/Sink and Work Done by Deformation Impacts on MHD Viscoelastic Fluid over a Nonlinear Stretching Sheet. World Journal of Mechanics, 3, 203-214.
- 16. Viskanta, R. and Grosh, R.J. (1962) Boundary Layer in Thermal Radiation Absorbing and Emitting Media. International Journal of Heat Mass Transfer, 5, 795-806.
http://dx.doi.org/10.1016/0017-9310(62)90180-1 - 17. Bestman, A.R. (1990) The Boundary-Layer Flow past a Semi-Infinite Heated Porous Plate for a Two-Component Plasma. Astrophysics and Space Science, 173, 93-100.
http://dx.doi.org/10.1007/BF00642565 - 18. Sattar, M.A. and Alam, M.M. (1994) Thermal-Diffusion as Well as Transpiration Effects on MHD Free Convection and Mass Transfer Flow past an Accelerated Vertical Porous Plate. Indian Journal of Pure and Applied Mathematics, 25, 679-688.
NOTES
*Corresponding author.































































