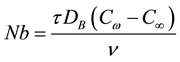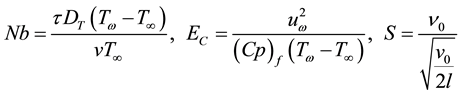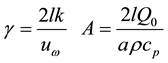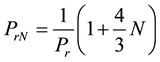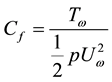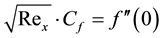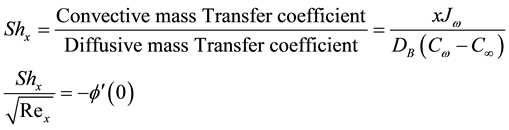World Journal of Mechanics
Vol.05 No.11(2015), Article ID:61073,11 pages
10.4236/wjm.2015.511020
Magneto Hydrodynamics Stagnation Point Flow of a Nano Fluid over an Exponentially Stretching Sheet with an Effect of Chemical Reaction, Heat Source and Suction/Injunction
Ch. Achi Reddy1∗, B. Shankar2
1M.L.R. Institute of Technology, Dundigal, Hyderabad, India
2Professor, Department of Mathematics, Osmania University, Hyderabad, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 11 July 2015; accepted 10 November 2015; published 13 November 2015

ABSTRACT
A numerical investigation is carried out on the effects of heat source suction and viscous dissipation on Magneto hydrodynamics boundary layer flow of a viscous, steady and incompressible fluid. The flow is assumed to be over on exponentially stretching sheet. The governing system of partial differential equations has been transformed into ordinary differential equation using similarity transformation. Keller box method is simulated on the dimensionless system of differential equations. The skin friction coefficient and the heat and mass transfer rates are very significant parameters that are computed, analysed discussed in detail.
Keywords:
Boundary Layer Flow, Exponentially Stretching Sheet, Keller Box Method, Heat Source, Suction, Chemical Reaction and Viscous Dissipation

1. Introduction
Stagnation point is of considerable importance in most of industrial applications. The stagnation point is the one where fluid becomes stationary. In certain situations, flow is stagnated by a solid wall while in others; there is a line interior to a homogeneous fluid domain or the interface between two immiscible fluids [1] -[3] . A good amount of research is done drawing the attention of several researchers [4] -[14] .
A new kind of fluid known as Nano fluid is first time proposed in Argonne National Laboratory in US by Chai at the time of investigations on coolants techniques and cooling processes. The Nano fluids are of nanometre sized particles that are metals, oxides and nanotubes.
The properties of Nano fluids are of special importance over the base fluid since thermal conductivity and convective properties of the Nano fluid predominant over the properties of the base fluid. Thermal conductivity is observed to be more effectively enhanced in the range of 15% - 40% over the base fluid. Stagnation point flow is most significant in various fields of science and technology. The study of stagnation point flow was carried out by Hiemenz in 1911 [15] who concentrated his studies on the two-dimensional stagnation point problem. Magyari and Keller [16] investigated the steady boundary layers flow on a stretching continuous surface with exponential temperature distribution while Partha et al. and M. Shakhaoath Khan [17] [18] analysed the effects of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface. However, researchers are getting interested in studying the boundary layer flow of Nano fluids with different aspects [19] - [36] .
In the present study, we have investigated the viscous dissipation, heat source, suction for different values of velocity ratio parameter and observed that the nanoparticle volume decreases with the increase of chemical reaction parameter for γ = 0.1 and 2.1.
2. Mathematical Formulation
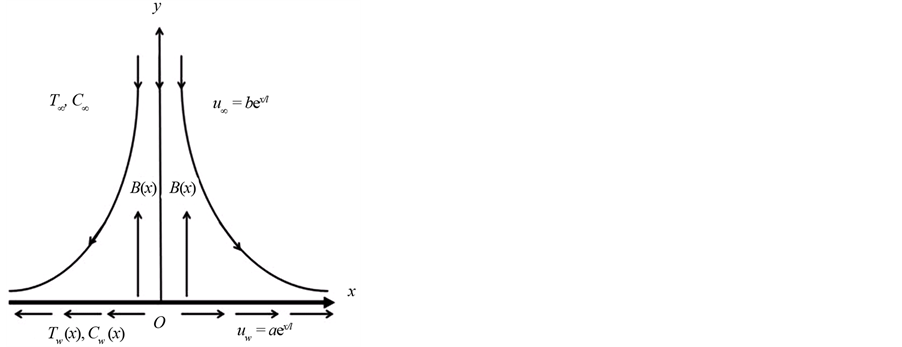
Consider a steady, two-dimensional boundary layer stagnation-point flow of a Nano fluid over an exponentially stretching sheet, the stretching and free stream velocities are assumed to be of the forms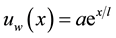 , and
, and , respectively. Where a > 0 and b are constants, x is the coordinate measure along the stretching surface and l is length of the sheet. A non-uniform transverse magnetic field of strength
, respectively. Where a > 0 and b are constants, x is the coordinate measure along the stretching surface and l is length of the sheet. A non-uniform transverse magnetic field of strength 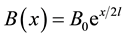 is imposed parallel to the y-axis, where Bo is a uniform magnetic field strength. It is assumed that the induced magnetic field due to the motion of an electrically conducting field is negligible. Further it is also assumed that the external electric field is zero and the electrical field due to polarization of charges is negligible [22] .
is imposed parallel to the y-axis, where Bo is a uniform magnetic field strength. It is assumed that the induced magnetic field due to the motion of an electrically conducting field is negligible. Further it is also assumed that the external electric field is zero and the electrical field due to polarization of charges is negligible [22] .
Figure 1 shows that the temperature T and the Nano-particles fraction C take forms Tω(x) and Cω(x), respectively whereas the ambient values of temperature T∞ and Nano-particle fraction C∞ are obtained when y tends to infinity.
The governing boundary layer equations of the conservation Law of mass, momentum, energy and concentration in the flow as follows:
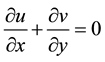 (1)
(1)
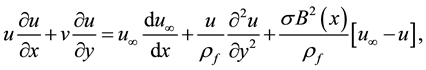 (2)
(2)
Figure 1. Physical flow model and coordinate system.
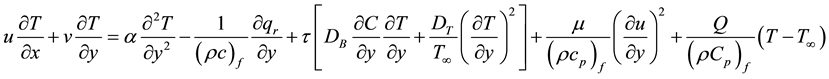 (3)
(3)
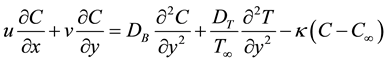 (4)
(4)
Here u and v are the velocity components in the x and y directions respectively, µ is the viscosity, ρ is the
density of the base field and σ is the electrical conductivity. 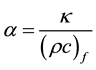 where k is the thermal conductivity and
where k is the thermal conductivity and 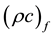 is the heat capacitance of the base fluid and
is the heat capacitance of the base fluid and 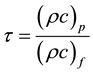 where
where 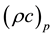 is the heat capacitance of
is the heat capacitance of
the nanoparticle. DB is the Brownian diffusion coefficient, DT is the thermophoresis diffusion coefficient and  is the radiation flux. The Rosseland approximation is defined as [23] [24] ;
is the radiation flux. The Rosseland approximation is defined as [23] [24] ;
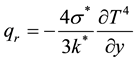 (5)
(5)
where σ∗ is the Stefan-Boltzmann constant and k∗ is the mean absorption coefficient. It is assumed that the temperature difference between the free stream T∞ and local temperature T is small enough expanding T4 in a Taylor series about T∞ and neglecting higher order terms results;
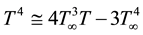 . (6)
. (6)
After substituting Equations (5) and (6) in Equation (3), it will be reduced to
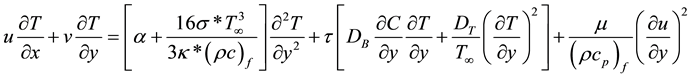
the subjected boundary conditions are
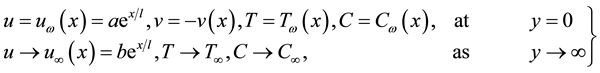
The prescribed temperature and concentration on the surface of the sheet is assumed to be 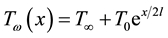
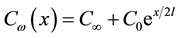
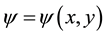
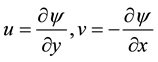
where the continuity Equation (1) is satisfied identically. A similarity transformation is defined as [20] follows
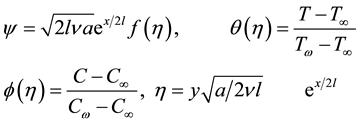
as such Equation (10), Equations (2), (4) and (7) reduce to the following system of nonlinear ordinary differen- tial equations.
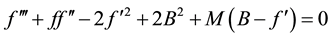
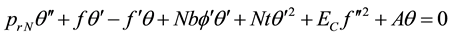
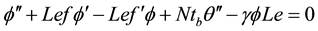
where
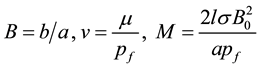
Here, prime denote the differentiation with respect to 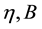
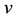
where 
where Nb is the Brownian motion parameter and Nt is the thermophoresis parameter, Ec Eckert number, γ is chemical reaction parameter; The corresponding boundary conditions Equation (8) are transformed into
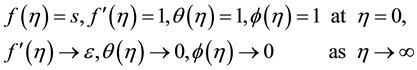
The parameters of practical interest in the formulated problem are velocity, heat and mass transfer respectively, which are presented in terms of Skin friction Cf, Nusselt number Nu and Sherwood numbers Sh. Using the transformed variables (10), the non-dimensional expressions for the Skin friction coefficient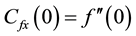

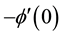
Skin friction coefficient:
The Skin friction coefficient 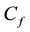
where τω is the local wall Shear stress, ρ is the fluid density.
Nusselt Number:
In heat transfer at a boundary within a fluid, the Nusselt number (Nu) is the ratio of convection to conductive heat transfer across the boundary

Sherwood Number:
The Sherwood number (Sh) is also called the mass transfer Nusselt number. It represents the ratio of convective to diffusive mass transport
where 
3. Numerical Procedure
The equations (11)-(14) subject to the boundary conditions (15) are solved numerically using an implicit finite-difference scheme known as Keller box method. The method has the following four basic steps.
1) Reduce equations (11)-(14) to first order equations;
2) Write the difference equations using central differences;
3) Linearize the resulting algebraic equations by Newton’s method and write them in matrix-vector;
4) Use the Block-tridiagonal elimination technique to solve the linear system.
The system of ordinary differential equations (11)-(13) has been solved numerically using Keller-box method. From the numerical computation, the main physical quantities of interest namely the local skin friction coefficient, the local Nusselt number and the local Sherwood number are obtained and the results are presented in Table 1, Table 2 and Table 3.
From Table 2, it is observed that with the increase in heat source parameter, there is a decrease in rate of heat transfer and increase in mass transfer.
From Table 3, it is observed that with increase in suction parameter, there is a increase in rate of heat transfer, mass transfer and skin friction coefficient.
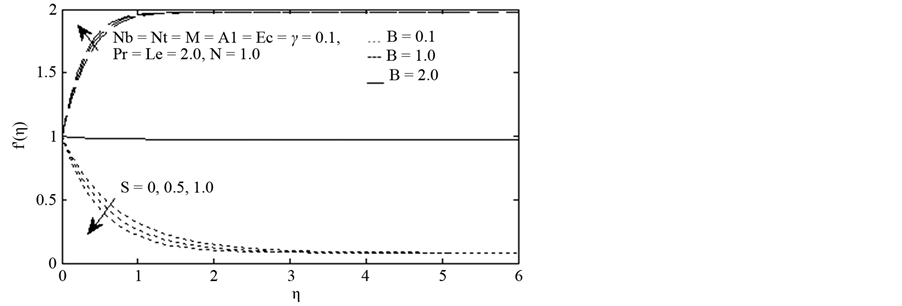
Figure 2 shows the effects of the suction parameter “s” on the flow field velocity f′(η) for three different values of the velocity ratio parameter B, B = 0.1, 1 and 2.
When B = 0.1 the velocity profile and the boundary layer thickness decrease with an increases in “s”. When s = 2.0, higher value of the Lorentz force further reduces the velocity and consequently the thickness of boundary
Table 1. Comparison of the reduced Nusselt number 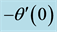
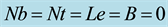
Figure 2. Velocity profile against η for different values of S.
Table 2. Values of the reduced Nusselt number
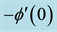
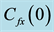
Table 3. Values of the reduced Nusselt number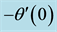
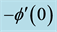
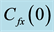
layer reduces. When B = 1, there is no influence of source on f′(η) and f′(η) attains a constant value of “1” for any values of η indicating that there is no boundary layer of fluid, as shown by a thick (-) line in Figure 2.
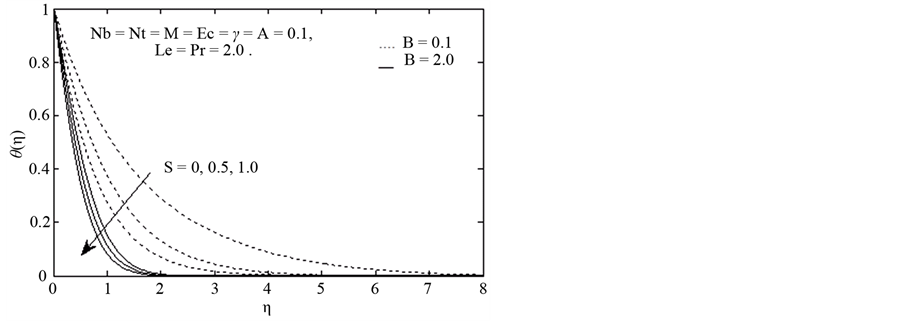
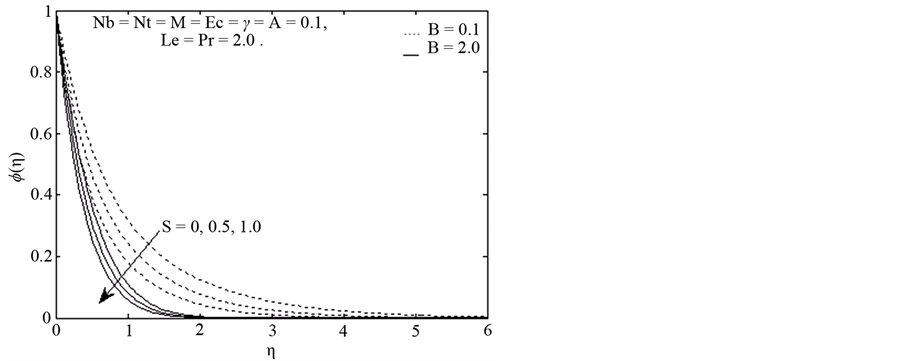
Figure 3 and Figure 4 demonstrate the effects of suction parameter on temperature and concentration. It is clear that the fluid velocity decreases significantly with increasing values of suction parameter while it is found to enhance with blowing. The presence of suction would result in the reduction of the thickness of the boundary layer. So the Nano fluid temperature and concentration decreases with an increase in the suction parameter.
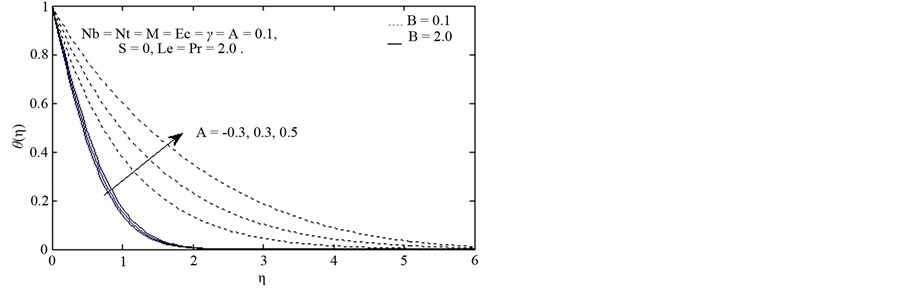
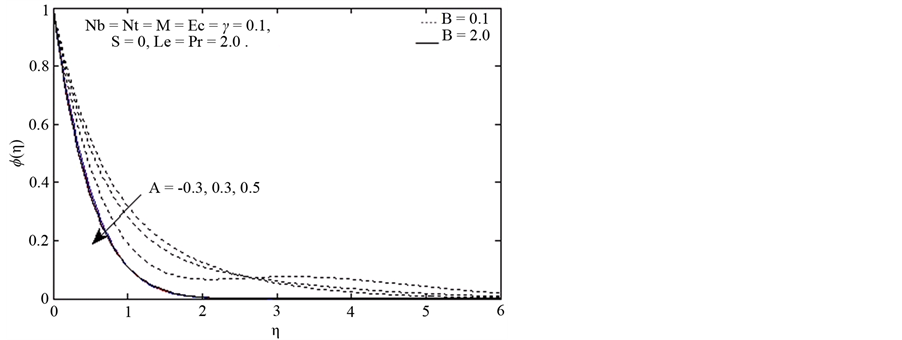
Figure 5 shows effects of the heat source parameter on temperature. Increasing the heat source parameter from −0.3 to 0.5 increases the temperature profile. Because the presence of source of heat enhances thermal energy, as a result of this, temperature profile increases. Figure 6 shows the heat source parameter significantly decreases the concentration profile.
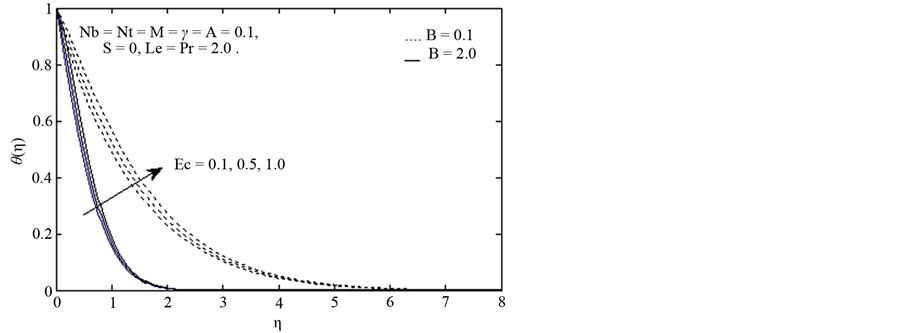
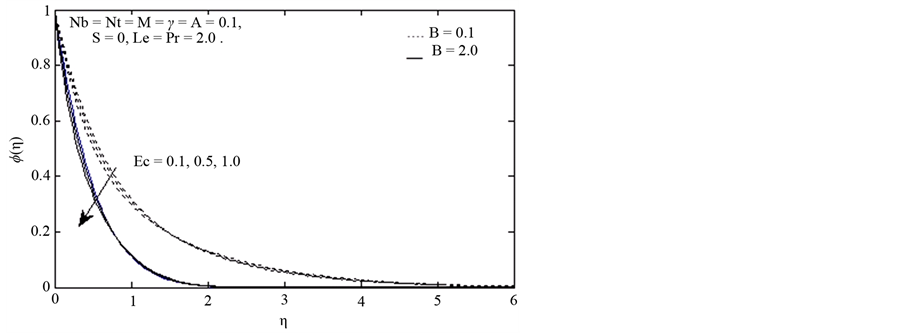
Figure 7 and Figure 8 shows the effects of viscous dissipation parameter “Ec” on Temperature and concentration profile. Eckert number is the ratio of the kinetic energy of the flow to the boundary Layer enthalpy differ-
Figure 3. Temperature profile against η for different values of S.
Figure 4. Concentration profile against η for different values of S.
Figure 5. Temperature profile against η for different values of A.
ence. The effect of viscous dissipation on flow field is to increase the energy, yielding a greater fluid temperature and as consequence greater buoyancy force. The increase in the buoyancy force due to an increase in the dissipation parameter enhances the temperature. While concentration decreases with an increase in the viscous dissipation parameter.
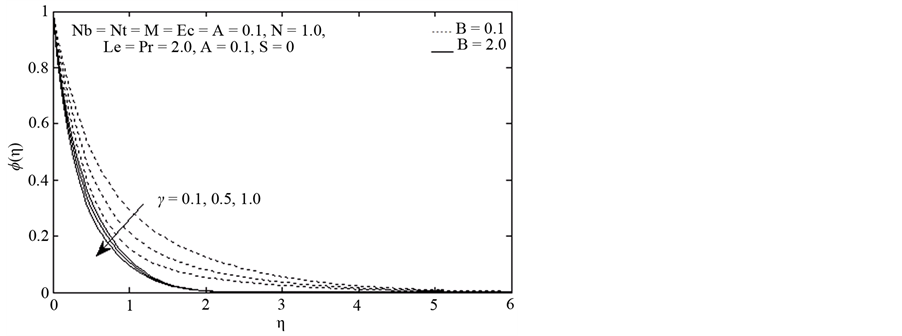
The influence of chemical reaction parameter “γ” on concentration profile is shown in Figure 9. Concentration decreases with an increase in the chemical reaction parameter indicating that the nanoparticle volume fraction decreases with the increase of chemical reaction parameter, while effect of chemical reaction parameter γ is
Figure 6. Concentration profile against η for different values of A.
Figure 7. Temperature profile against η for different values of Ec.
Figure 8. Concentration profile against η for different values of Ec.
not significant on the temperature profile.
4. Conclusions
A numerical study corresponding to the flow and heat transfer in a steady flow region of Nano fluid over an exponential stretching surface and effects of heat source, suction parameter and Eckert number are examined and
Figure 9. Concentration profile against η for different values of γ.
discussed in detail. The main observation of the present study as follows:
1) It is interesting to note that an increase in the suction parameter reduces the velocity profile and increase the temperature and concentration;
2) An increase in the heat source parameter increases the temperature profile while it reduces the concentration profile;
3) An increase in the Eckert number increases the temperature profile while it reduces the concentration profile.
Cite this paper
Ch. AchiReddy,B.Shankar, (2015) Magneto Hydrodynamics Stagnation Point Flow of a Nano Fluid over an Exponentially Stretching Sheet with an Effect of Chemical Reaction, Heat Source and Suction/Injunction. World Journal of Mechanics,05,211-221. doi: 10.4236/wjm.2015.511020
References
- 1. Hiemenz, K. (1911) Die Grenzschicht an einem inden gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder, Dingler’s Polytech. J., 326, 321-324.
- 2. Wong, K.V. and Leon, O.D. (2010) Applications of Nanofluids: Current and Future. Advances in Mechanical Engineering, 1-12
- 3. Mahapatra, T.R. and Gupta, A.S. (2002) Heat Transfer in Stagnation-Point Flow towards a Stretching Sheet. Heat and Mass Transfer, 38, 517-521.
http://dx.doi.org/10.1007/s002310100215 - 4. Mahapatra, T.R. and Gupta, A.S. (2003) Stagnation-Point Flow towards a Stretching Surface. The Canadian Journal of Chemical Engineering, 81, 258-263.
http://dx.doi.org/10.1002/cjce.5450810210 - 5. Nazar, R., Amin, N., Filip, D. and Pop, I. (2004) Stagnation Point Flow of a Micropolar Fluid towards a Stretching Sheet. International Journal of Non-Linear Mechanics, 39, 1227-1235.
http://dx.doi.org/10.1016/j.ijnonlinmec.2003.08.007 - 6. Lok, Y.Y., Amin, N. and Pop, I. (2006) Non-Orthogonal Stagnation Point Flow towards a Stretching Sheet. International Journal of Non-Linear Mechanics, 41, 622-627.
http://dx.doi.org/10.1016/j.ijnonlinmec.2006.03.002 - 7. Nadeem, S., Hussain, A. and Khan, M. (2010) HAM Solutions for Boundary Layer Flow in the Region of the Stagnation Point towards a Stretching Sheet. Communications in Nonlinear Science and Numerical Simulation, 15, 475-481.
http://dx.doi.org/10.1016/j.cnsns.2009.04.037 - 8. Labropulu, F., Li, D. and Pop, I. (2010) Non-Orthogonal Stagnation-Point Flow towards a Stretching Surface in a Non-Newtonian Fluid with Heat Transfer. International Journal of Thermal Sciences, 49, 1042-1050.
http://dx.doi.org/10.1016/j.ijthermalsci.2009.12.005 - 9. Ishak, A., Lok, Y.Y. and Pop, I. (2010) Stagnation-Point Flow over a Shrinking Sheet in a Micropolar Fluid. Chemical Engineering Communications, 197, 1417-1427.
http://dx.doi.org/10.1080/00986441003626169 - 10. Bachok, N., Ishak, A. and Pop, I. (2010) Boundary-Layer Flow of Nanofluid over a Moving Surface in a Flowing Fluid. International Journal of Thermal Sciences, 49, 1663-1668.
http://dx.doi.org/10.1016/j.ijthermalsci.2010.01.026 - 11. Patel, M. and Timol, M.G. (2011) Orthogonal Stagnation Point Flow of a Power Law Fluid towards a Stretching Surface. International Journal of Applied Mathematics and Mechanics, 7, 31-37.
- 12. Bachok, N., Ishak, A. and Pop, I. (2011) On the Stagnation Point Flow towards a Stretching Sheet with Homogeneous-Heterogeneous Reactions Effects. Communications in Nonlinear Science and Numerical Simulation, 16, 4296-4302.
http://dx.doi.org/10.1016/j.cnsns.2011.01.008 - 13. Choi, S.U.S., Zhang, Z.-G., Yu, W., Lockwood, F.E. and Grullce, E.A. (2001) Anomalous Thermal Conductivity Enhancement in Nanotube Suspensions. Applied Physics Letters, 79, 2252.
http://dx.doi.org/10.1063/1.1408272 - 14. Yu, W., France, D.M., Routbort, J.L. and Choi, S.U.S. (2008) Review and Comparison of Nanofluid Thermal Conductivity and Heat Transfer Enhancements. Heat Transfer Engineering, 29, 432-460.
http://dx.doi.org/10.1080/01457630701850851 - 15. Bachok. N., Ishak, A. and Pop, I. (2010) Melting Heat Transfer in Boundary Layer Stagnation—Point Flow Towards a Stretching/Shrinking Sheet. Physics Letters A, 374, 4075-4079.
- 16. Magyari, E. and Keller, B. (1999) Heat and Mass Transfer in the Boundary Layers on an Exponentially Stretching Continuous Surface. Journal of Physics D, 32, 577-585.
http://dx.doi.org/10.1088/0022-3727/32/5/012 - 17. Partha, M.K., Murthy, P.V.S.N. and Rajasekhar, G.P. (2005) Effect of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface. Heat and Mass Transfer, 11, 360-366.
http://dx.doi.org/10.1007/s00231-004-0552-2 - 18. Khan, M.S., Karim, I. and Islam, M.S. (2014) Possessions of Chemical Reaction on MHD Heat and Mass Transfer Nanofluid Flow on a Continuously Moving Surface. The American Chemical Science Journal, 4, 401-415.
http://dx.doi.org/10.9734/ACSJ/2014/5422 - 19. Bidin, B. and Nazar, R. (2009) Numerical Solution of the Boundary Layer Flow over an Exponentially Stretching Sheet with Thermal Radiation. European Journal of Scientific Research, 33, 710-717.
- 20. Ishak, A. (2011) MHD Boundary Layer Flow Due to an Exponentially Stretching Sheet with Radiation Effect. Sains Malaysiana, 40, 391-395.
- 21. Anwar, I., Shafie, S. and Salleh, M.Z. (2014) Radiation Effect on MHD Stagnation Point Flow of a Nanofluid over an Exponentially Stretching Sheet. Walailak Journal of Science and Technology, 11, 569-591.
- 22. Chen, C.H. (2008) Effects of Magnetic Field and Suction/Injection on Convection Heat Transfer of Non-Newtonian Power-Law Fluids Past a Power-Law Stretched Sheet with Surface Heat Flux. International Journal of Thermal Sciences, 47, 954-961.
http://dx.doi.org/10.1016/j.ijthermalsci.2007.06.003 - 23. Cess, R.D. (1966) The Interaction of Thermal Radiation with Free Convection Heat Transfer. International Journal of Heat and Mass Transfer, 9, 1269-1277.
http://dx.doi.org/10.1016/0017-9310(66)90119-0 - 24. Hady, F.M., Ibrahim, F.S., Abdel-Gaied, S.M. and Eid, M.R. (2012) Radiation Effect on Viscous Flow of a Nanofluid and Heat Transfer over a Nonlinearly Stretching Sheet. Nanoscale Research Letters, 7, 229.
http://dx.doi.org/10.1186/1556-276X-7-229 - 25. El-Aziz, M.A. (2009) Viscous Dissipation Effect on Mixed Convection Flow of a Micropolar Fluid over an Exponentially Stretching Sheet. Canadian Journal of Physics, 87, 359-368.
http://dx.doi.org/10.1139/P09-047 - 26. Partha, M.K., Murthy, P.V.S.N. and Rajasekhar, G.P. (2005) Effect of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface. Heat and Mass Transfer, 41, 360-366.
http://dx.doi.org/10.1007/s00231-004-0552-2 - 27. Khan, M.S., Karim, I., Ali, L.E. and Ismail, A. (2012) Unsteady MHD Free Convection Boundary-Layer Flow of a Nanofluid along a Stretching Sheet with Thermal Radiation and Viscous Dissipation Effects. International Nano Letters, 2, 24.
http://dx.doi.org/10.1186/2228-5326-2-24 - 28. Hamad, M.A., Pop, I. and Ismail, A.I. (2011) Magnetic Field Effects on Free Convection Flow of a Nanofluid Past a Vertical Semi-Infinite Flat Plate. Nonlinear Analysis: Real World Applications, 12, 1338-1346.
http://dx.doi.org/10.1016/j.nonrwa.2010.09.014 - 29. Jafar, K., Nazar, R., Ishak, A. and Pop, I. (2011) MHD Flow and Heat Transfer over Stretching/Shrinking Sheets with External Magnetic Field, Viscous Dissipation and Joule Effects. The Canadian Journal of Chemical Engineering, 90, 1336-1346.
http://dx.doi.org/10.1002/cjce.20609 - 30. Reddy, M.G. (2011) Influence of the Thermal Radiation, Viscous Dissipation and Hall Current on MHD Convection Flow over a Stretched Vertical Flat Plate. Ain Shams Engineering Journal, 3, 169-175.
- 31. Vajravelu, K. and Hadjinicolaou, A. (1993) Heat Transfer in a Viscous Fluid over a Stretching Sheet with Viscous Dissipation and Internal Heat Generation. International Communications in Heat and Mass Transfer, 20, 417-430.
http://dx.doi.org/10.1016/0735-1933(93)90026-R - 32. Postelnicu, A. (2007) Influence of Chemical Reaction on Heat and Mass Transfer by Natural Convection from Vertical Surfaces in Porous Media Considering Soret and Dufour Effects. Heat and Mass Transfer, 43, 595-602.
http://dx.doi.org/10.1007/s00231-006-0132-8 - 33. Goyal, M. and Bhargava, R. (2013) Numerical Solution of MHD Viscoelastic Nanofluid Flow over a Stretching Sheet with Partial Slip and Heat Source/Sink. ISRN Nanotechnology, 2013, Article ID: 931021.
- 34. Cebeci, T. and Bradshaw, P. (1988) Physical and Computational Aspects of Convective Heat Transfer. Springer, New York.
- 35. Vendabai, K. and Sarojamma, G. (2014) Unsteady Convective Boundary Layer Flow of a Nanofluid over a Stretching Surface in the Presence of a Magnetic Field and Heat Generation. International Journal of Emerging Trends in Engineering and Development, 3, 214-230.
- 36. Dulal, P. and Hiranmoy, M. (2012) Non-Darcian Buoyancy Driven Heat and Mass Transfer over a Stretching Sheet in a Porous Medium with Radiation and Ohmic Heating. International Journal of Nonlinear Science, 14, 115-123.
NOTES
*Corresponding author.