World Journal of Mechanics
Vol.05 No.08(2015), Article ID:59271,11 pages
10.4236/wjm.2015.58015
A Novel Technique for Evaluating Failure Probability of Random Structure
Seifedine Kadry1, Abdelkhalak El Hami2
1American University of the Middle East, Egaila, Kuwait
2INSA of Rouen Institute, Normandy University, St. Etienne du Rouvray, France
Email: skadry@gmail.com, abdelkhalak.elhami@insa-rouen.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 July 2015; accepted 28 August 2015; published 31 August 2015
ABSTRACT
The purpose of this article is to develop a new methodology to evaluate the statistical characteristic of the response of structures subjecting to random excitation, by combining the Finite Element Method (FEM) with the Transforming Density Function (TDF). Uncertainty modeling of structure with random variables encourages the coupling of advanced TDF for reliability analysis to analyze problems of stochastic mechanical systems. The TDF is enthusiastically applicable in the situation where the relationship between input and output of structures is available in explicit analytical form. However, the situation is much more involved when it is necessary to perform the evaluation of implicit expression between input and output of structures through numerical models. For this aim, we propose a new technique that combines the FEM software, and the TDF method to evaluate the most important statistical parameter the Probability Density Function (PDF) of the response where the expression between input and output of structures is implicit. Once the PDF is evaluated, all other statistical parameters are derived easily. This technique is based on the numerical simulations of the FEM and the TDF by making a middleware between Finite Element software and Matlab. Some problems, range from simple to complex, of structures are analyzed using our proposed technique. Its accuracy is validated through Monte-Carlo simulation.
Keywords:
Random Parameter, Uncertainty, Transforming Density Function, Finite Element Method, Finite Element Software, Matlab, Structures

1. Introduction
Many applications in mechanics require consideration of stochastic properties of materials, geometry or loads. The problem of reliability analysis of stochastic mechanical systems is of central importance in the safety assessment of structures. In a stochastic system, a large number of random variables influence the performance of the system, e.g. young’s modulus, external loads… The performance of the system is evaluated by a best-esti- mate code. Consider a performance criterion Y of the system depending on the input variables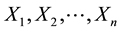 . the function
. the function  is a random variable to be determined. In order to get the information about the uncertainty of Y, a number of FE runs have to be performed. For each of these runs, all identified uncertain parameters are varied simultaneously. According to the exploitation of the result of these studies, the uncertainty on the response can be evaluated either in the form of an uncertainty range, or in the form of a probability density function.
is a random variable to be determined. In order to get the information about the uncertainty of Y, a number of FE runs have to be performed. For each of these runs, all identified uncertain parameters are varied simultaneously. According to the exploitation of the result of these studies, the uncertainty on the response can be evaluated either in the form of an uncertainty range, or in the form of a probability density function.
Reliability methods focus on the calculation of the probability of failure associated with a limit-state function. First-order and second-order reliability approximations methods (FORM and SORM) and various simulation methods are commonly used in reliability analysis [1] . Because of the typically high level of reliability of civil structures, the failure probability is usually small (in the order of 102 - 106). To account for the spatial variability of uncertain quantities (for instance, that of a material property), a characterization in terms of a random field is usually employed. Through a process of discretization, it is possible to represent the random field by a vector of random variables. One of the methods mentioned above may then be used to carry out second-moment or reliability analysis. The spectral stochastic finite element method (SSFEM) proposed by Ghanem and Spanos [2] - [5] is an approach well suited to analysis involving random fields. It is based on two discretization of the system of (stochastic) partial differential equations governing the problem under consideration, one in the spatial domain and one in the probabilistic domain. The response (e.g. the random vector of nodal displacements) is cast as a series expansion in standard normal random variables. This can be interpreted as an “intrinsic” representation of the random response, from which quantities such as statistical moments can be computed by post- processing, either analytically or by simulation.
In this paper, a proposed technique: the Finite Element Method (FEM) software coupled with the Transforming Density Function (TDF) program is applied in order to evaluate numerically the probabilistic and statistical characteristics of the response of stochastic mechanical system. To demonstrate the efficiency of the proposed technique, we have carried out different applications to cover several structural problems
2. Reliability Analysis
Reliability methods aim at evaluating the probability of failure of a system whose modeling takes into account randomness. The design of structures and the prediction of their good functioning lead to the verification of a certain number of rules resulting from the knowledge of physical and mechanical experience of designers and constructors. These rules traduce the necessity to limit the loading effects such as stresses and displacements. Each rule represents an elementary event and the occurrence of several events leads to a failure scenario. The objective is then to evaluate the failure probability corresponding to the occurrence of critical failure modes. In addition to the vector of deterministic variables x to be used in the system control and optimization, the uncertainties are modeled by a vector of stochastic physical variables Y affecting the failure scenario. The knowledge of these variables is not, at best, more than statistical information and we admit a representation in the form of random variables. For a given design rule, the basic random variables are defined by their probability distribution associated with some expected parameters; the vector of random variables is noted herein Y whose realizations are written y. The safety is the state where the structure is able to fulfill all the functioning requirements: mechanical and serviceability, for which it is designed. To evaluate the failure probability with respect to a chosen failure scenario, a limit state function  is defined by the condition of good functioning of the structure. The limit between the state of failure
is defined by the condition of good functioning of the structure. The limit between the state of failure  and the state of safety
and the state of safety 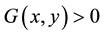 is known as the limit state surface
is known as the limit state surface  (Figure 1). The failure probability is then calculated by [1] :
(Figure 1). The failure probability is then calculated by [1] :
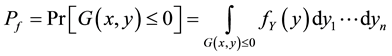 (1)
(1)
where Pf is the failure probability, fY(y) is the joint density function of the random variables Y and Pr [6] is the probability operator. The evaluation of integral (1) is not easy, because it represents a very small quantity and all the necessary information for the joint density function are not available. For these reasons, the First and the Second Order Reliability Methods FORM/SORM have been developed. They are based on the reliability index
Figure 1. Physical and normalized spaces.
concept, followed by an estimation of the failure probability. The invariant reliability index β was introduced by working in the space of standard independent Gaussian variables instead of the space of physical variables. The transformation from the physical variables y to the normalized variables u is given by:
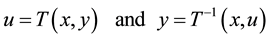 (2)
(2)
This transformation T(.) is called the probabilistic transformation. In this standard space, the limit state function takes the form:
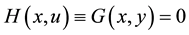 (3)
(3)
For practical engineering, Equation (3) gives sufficiently accurate estimation of the failure probability.
2.1. Approximate Reliability Methods (FORM & SORM)
The First Order Reliability Method (FORM) uses the closest point on the limit state function H(u) = 0 to the origin in the standard normal space as a measure of the reliability. This point is called design point  and its absolute beta value
and its absolute beta value  specifies the reliability or complementary the failure probability
specifies the reliability or complementary the failure probability ,
,
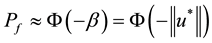 , where
, where 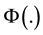 denotes the standard normal cumulative distribution function. FORM
denotes the standard normal cumulative distribution function. FORM
leads to exact results in case a single linear limit state function H(u) = 0 is considered.
Second Order Reliability Methods (SORM) approximate the limit state function by an incomplete second order polynomial, which assumes in a rotated space the simple form
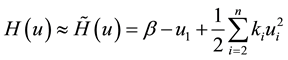 (4)
(4)
The form is incomplete since the terms
around the design point, are missing. An exact result in form of a one dimensional integral has been derived in [7] for the incomplete representation and an asymptotic result, sufficiently accurate for large 
2.2. Importance Sampling
Importance Sampling has been one of the most prevalent approaches in the context of Simulation based methods for the estimation of structural reliability [9] . The underlying concept is to draw samples of the vector of random parameters y from a distribution 
2.3. Line Sampling
An alternative, quite suitable for large dimension n and efficient in context with FEA, is the following approach denoted as “line sampling”. It requires an important direction a as starting point, defining the direction along the limit state G(x, y) will be determined. Each point (x, y) in the standard point is decomposed into the one dimensional space [10] .
2.4. Some Factors of Comparison
Procedures for estimating probabilities of failure developed over the last twenty years like FORM/SORM, Importance Sampling, and all its variants built on it, lack robustness or computational efficiency as the number of random variables (dimension n) tends to infinity. However, the robust and simple straight forward Line sampling procedures is able to overcome most difficulties encountered in traditional procedures. Summarizing the arguments, the following can be concluded:
・ FORM provides a point estimate, subject to linearization errors, without confidence. Moreover, it requires the evaluation of the design point, which becomes difficult in high dimension for nonlinear limit state functions in the standard normal space. The efforts to compute the design point grows proportional with the dimension n.
・ SORM requires in addition to the design point n > 1 main curvature with cannot be obtained in a feasible manner for high dimensions n. The procedure implies that the domain close to the design point is the important domain which is not the case for high dimensions.
・ Importance Sampling is more robust and accurate as FORM or SORM, but not competitive to Line Sampling, because it is generally impossible to sample according to the optimal sampling density. The approach has difficulties to deal with multiple failure domains if they are not well separated.
Line Sampling is capable to take advantage of simple flat limit states in standard normal space and samples in the most important domain, without assuming a linear or quadratic limit state surface or requiring a design point computation.
3. Finite Element Method and TDF
3.1. Finite Element Method
The Finite Element Method is the standard tool for certain classes of partial differential equations arising in various fields of engineering and in particular for those arising in solid mechanics. For linear systems enforcing global static or dynamic equilibrium the FE Analysis leads to a system of linear equations, respectively


where the matrices K and M are the global stiffness and mass matrices, respectively, obtained by adding the contributions of all element matrices


where 






3.2. Transforming Density Function TDF
The Transforming Density Function is based on the following theorem
Theorem: Suppose that 












where 

TDF is based on one-to-one mapping between the random output(s) and input(s) where the transformation Jacobean J can be computed. The PDF of the output(s) is then computed through the known joint PDF of the inputs multiplied by the determinant of transformation Jacobean matrix. The idea of TDF is based on the following formula [11]



The general steps in the application of the TDF program: 1) the random variable input is generating and the stochastic equation of equilibrium is solved first using FEM software. 2) This solution is used to compute numerically the function between the input and the output by the Cubic Spline Interpolation, which is then inverted for the calculation of the determinant of the transformation Jacobean. Finally, the PDF of the response at any point in the domain can be deduced by using the formula (7). This approach has the advantage of giving a closed-form of the density function of the response, which is very helpful for reliability analysis of mechanical systems [3] [5] . To overcome the drawback of TDF, in analysis of complicated structures, we propose in this paper an interface between the FEM software and the TDF program.
4. Finite Element Method Coupled with Transforming Density Function: FEMCTDF
Before you begin to format your paper, first write and save the content as a separate text file. Keep your text and graphic files separate until after the text has been formatted and styled. Do not use hard tabs, and limit use of hard returns to only one return at the end of a paragraph. Do not add any kind of pagination anywhere in the paper. Do not number text heads―the template will do that for you.
Finally, complete content and organizational editing before formatting. Please take note of the following items when proofreading spelling and grammar:
The FEM software is used to perform the structural analysis to obtain the structure weight, maximal displacement, and maximal stress, corresponding to a set of given design variables. These analysis results are sent to the TDF program to conduct the Probabilistic Density Function PDF, and the probability of failure and generate new random variables. The newly generated variables are then used to update the input file. The FEM software is then invoked again to perform the structural analysis with the new input parameters. This process is repeated until satisfactory results are obtained.
4.1. Finite Element Analysis
Finite element codes are less complicated than many of the word processing and spreadsheet packages found on modern microcomputers. Nevertheless, they are complex enough that most users do not find it effective to program their own code. A number of prewritten commercial codes are available, representing a broad price range and compatible with machines from microcomputers to supercomputers 1. However, users with specialized needs should not necessarily shy away from code development, and may find the code sources available in such texts as that by Zienkiewicz 2 to be a useful starting point. Most finite element software is written in Fortran, but some newer codes such as felt are in C or other more modern programming languages. In practice, a finite element analysis usually consists of three principal steps:
1) Preprocessing: The user constructs a model of the part to be analyzed in which the geometry is divided into a number of discrete sub regions, or “elements,” connected at discrete points called “nodes.” Certain of these nodes will have fixed displacements, and others will have prescribed loads. These models can be extremely time consuming to prepare, and commercial codes vie with one another to have the most user-friendly graphical “preprocessor” to assist in this rather tedious chore. Some of these preprocessors can overlay a mesh on a preexisting CAD file, so that finite element analysis can be done conveniently as part of the computerized drafting-and-design process.
2) Analysis: The dataset prepared by the preprocessor is used as input to the finite element code itself, which constructs and solves a system of linear or nonlinear algebraic equations Kijuj = fi where u and f are the displacements and externally applied forces at the nodal points. The formation of the K matrix is dependent on the type of problem being attacked, and this module will outline the approach for truss and linear elastic stress analyses. Commercial codes may have very large element libraries, with elements appropriate to a wide range of problem types. One of FEA’s principal advantages is that many problem types can be addressed with the same code, merely by specifying the appropriate element types from the library.
3) Postprocessing: In the earlier days of finite element analysis, the user would pore through reams of numbers generated by the code, listing displacements and stresses at discrete positions within the model. It is easy to miss important trends and hot spots this way, and modern codes use graphical displays to assist in visualizing the results. A typical postprocessor display overlays colored contours representing stress levels on the model, showing a full-field picture.
4.2. Algorithm of Method FEMCTDF
We will implement our method in Matlab. The outline of the proposed technique FEMCTDF is as follows:
1) Generate the input random variables;
2) Calculate the value of output variables by FE software, for each value of input the correspondent value of output is estimating using FEM and it is stocking in solution file;
3) Approximate the function between input and output variables using Cubic Spline Interpolation;
4) Calculate the determinant of Jacobean of input and output variables (Equation (10));
5) Apply the basic relation of TDF (Equation (10));
6) Evaluate the graphic of PDF of output variable in function of this output variable (in our case the PDF of displacement in function of displacement);
7) Approximate the Probability of failure
We start with the creation of file variables. Out that serves to stock the random variables generating by TDF program in Matlab in order to use them by the executable file under FEM software. Once the FEM software receives these variables it introduces them in the modelling of the considered structure, and by the FEM and Static analysis done by the FEM software we get the results (nodal displacement, strains, and so on). These results are stocked in the file response. out. This later file is communicated to the TDF program in order to calculate the PDF of the output variable of the considered structure (in our case the vertical displacement uy) and the probability of failure of this structure.
5. Application
Three case studies presented in this section all have implicit function of output variable in terms of the input random variable. The proposed technique use the FEM for modelling the structure in every iteration and calculate the value of displacement (output variable) corresponding at each input variable value, and in other hand it would be necessary to use the TDF program for estimating the value of Pf (probability of failure) of the considered structure. In order to validate the FEMCTDF technique and to compare the results, the Monte Carlo Simulation is also employed as reference method for comparison.
5.1. Three Bar Truss
In this example, the three-bar truss (Figure 2 and Figure 3) is analysed using our proposed technique. For that purpose, statistic models must be defined for each random variable involved. Hence, uniform distribution in the range [5] [10] is assumed for the Young’s modulus E and the other parameters are considered as deterministic variables. These parameters (Geometrical and material proprieties) are: the section of each beam A = 1 m2, the length l = 3 m, the load W = 1.2 N, the mass density r = 7800 kg/m3.
From Figure 4, the PDF’s of the normalized vertical displacement uy of the 3bar structure calculated by our proposed technique FEMCTDF are independent and uniformly distributed in the range [1.2505; 2.5008].
Figure 2. Real application of three bar truss.
Figure 3. Three bar truss.
Also in this case the obtained results are accurate as shown by favourable comparison with classical Monte Carlo simulations. For Reliability Analysis, let us suppose that the limit displacement is

The numerical values of probabilistic characteristics of the displacement of this 3bar structure are listed in this Table 1.
5.2. Spatial Truss
This application treats structural analysis on one hand of the arrow of a crane of construction that one assimilates to a spatial truss. It is constituted by identical beams (Figure 5 and Figure 6). To the extremity of this truss is applied a load M = 5 t. The bars forming the structure are in steel of which Young’s modulus E is uniformly distributed in the range [100 GPa, 300 GPa] and the Poisson coefficient σ = 0.29. The bars have circular sections of which the big one is worth A1 = 22 mm2 and the small one A2 = 11 mm2. The weight of each of the bars of
Figure 4. PDF (u) when E is uniformly distributed.
Figure 5. Real application of spatial truss.
Figure 6. The spatial truss.
the truss is not negligible in front of the load M. The goal of this analysis is to determine the maximum displacement generated by the applied load to his extremity.
From Figure 7, the PDF’s of the normalized vertical displacement uy of the spatial truss calculated by our proposed technique FEMCTDF are independent and uniformly distributed in the range [0.00704, 0.02027]. Also the obtained results are accurate as shown by favourable comparison with classical Monte Carlo simulations. For Reliability Analysis, let us suppose that the limit displacement is ulimit =0.015 mm, It is required to find the failure probability Pf = P(u ≤ ulimit). The numerical values of probabilistic characteristics of the displacement of this spatial truss are listed in this Table 2.
Table 1. FEMCTDF versus Monte Carlo simulation.
Table 2. FEMCTDF versus Monte Carlo simulation.
Figure 7. PDF (u) when E is uniformly distributed.
5.3. Pylon of a Line of Transportation of Electricity
We are going to analyze the reliability of a more complex structure, the pylon of a line of transportation of electricity. Two identical loads F of 1.8 KN are applied to the two superior extremities of the following pylon an angle of

The PDFs of the normalized vertical displacement uy are plotted in Figure 10 assuming that the variable uy is independent and uniformly distributed in the range [2.9489e04, 8.8466e04]. Also in this case the results are accurate as shown by favorable comparison with classical Monte Carlo simulation. Let us suppose the limit displacement is u = 6.635e04 mm. It is required to find the failure probability Pf = P(u ≤ ulimit). Mean Squared Error (MSE), and Absolute Percentage Error (APE) are calculated by using the following equation:
Figure 8. Real application of pylon.
Figure 9. The pylon.
where u1 is displacement obtained with FEMCTDF and umc the Monte Carlo simulation one.
Table 3 reports the results (Umax, Umin, Umean are in mm) obtained by our technique and the Monte Carlo simulation (10,000 iterations). This table also illustrates the efficiency of the FEMCTDF, since a number of 800 (less than 1000) iterations suffice to obtain results close to those obtained by Monte Carlo simulation. To compare the results, the MSE and APE are calculated. The values of MSE and APE are very small, which shows the accuracy and efficiency of FEMCTDF.
6. Conclusion
In this paper, an efficient, robust technique is proposed to solve the reliability problems that required the evaluation
Figure 10. PDF (u) when E is uniformly distributed.
Table 3. FEMCTDF versus Monte Carlo simulation.
of implicit function between the input variable of the structure and his response variable. This technique has been developed with the motivation to facilitate the application of structural reliability analysis methods to numerical models of mechanical structures. It integrates the treatment by the FEM software and the TDF program. In fact, the FEM is used to estimate the structural response function, once the implicit response function is numerically found that the TDF program can easily be applied to solve the structural reliability problem.
Cite this paper
SeifedineKadry,Abdelkhalak ElHami, (2015) A Novel Technique for Evaluating Failure Probability of Random Structure. World Journal of Mechanics,05,139-150. doi: 10.4236/wjm.2015.58015
References
- 1. Kadry, S. (2007) A Proposed Method for Reliability Analysis in Higher Dimension. Engineering Letters, 15, 7-12.
- 2. Liu, W.-K., Belytschko, T. and Mani, A. (1986) Random Field Finite Elements. International Journal for Numerical Methods in Engineering, 23, 1831-1845.
http://dx.doi.org/10.1002/nme.1620231004 - 3. Deodatis, G. (1991) The Weighted Integral Method, I: Stochastic Stiffness Matrix. Journal of Engineering Mechanics, 117, 1851-1864.
- 4. Ditlevsen, O. and Madsen, H. (1996) Structural Reliability Methods. Wiley, Chichester.
- 5. Ghanem, R.-G. and Spanos, P.-D. (1991) Stochastic Finite Elements—A Spectral Approach. Springer, Berlin.
http://dx.doi.org/10.1007/978-1-4612-3094-6 - 6. Kadry, S., Chateauneuf, A. and El-Tawil, K. (2006) One Dimensional Transformation Methods in Reliability Analysis. CST, Madrid.
- 7. Tvedt, L. (1990) Distribution of Quadratic Forms in Normal Space-Application to Structural Reliability. Journal of Engineering Mechanics, 116, 1183-1197.
http://dx.doi.org/10.1061/(ASCE)0733-9399(1990)116:6(1183) - 8. Breitung, K. (1994) Asymtotic Approximations for Probability Integrals. Lecture Notes in Mathematics, 1592. Springer, Berlin.
- 9. Schueller, G. (1998) Structural Reliability-Recent Advances-Freudenthal Lecture. In: Shiraishi, N., Shinozuka, M. and Wen, Y., Eds., Proceedings of the 7th International Conference on Structural Safety and Reliability (ICOSSAR’97), A.A. Balkema Publications, Rotterdam, 3-35.
- 10. Koutsourelakis, P., Pradlwarter, H. and Schuëller, G. (2003) Reliability of Structures in High Dimensions. Proceedings in Applied Mathematics and Mechanics, 3, 495-496.
http://dx.doi.org/10.1002/pamm.200310517 - 11. Papoulis, A. and Pillai, S.U. (2002) Probability, Random Variables and Stochastic Processes. 4th Edition, McGraw-Hill, Boston.













