World Journal of Mechanics
Vol.06 No.09(2016), Article ID:70778,32 pages
10.4236/wjm.2016.69022
Effect of Mechanical Vibrations on Human Body
Mohammad AlShabi1, Walaa Araydah2, Hani ElShatarat2, Mohammad Othman3, Mohammed Bani Younis4, Stephen Andrew Gadsden5
1Mechanical Engineering Department, University of Sharjah, Sharjah, United Arab Emirates
2Department of Mechatronics Engineering, Philadelphia University, Philadelphia, PA, USA
3Department of Mechanical Engineering, Jordan University of Science and Technology, Al Ramtha, Jordan
4Department of Computer Engineering, Philadelphia University, Philadelphia, PA, USA
5School of Engineering, University of Guelph, Guelph, Ontario, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 11, 2015; Accepted: September 19, 2016; Published: September 22, 2016
ABSTRACT
Mechanical vibrations cause forces that affect human bodies. One of the most common positions for human bodies is the seated position. In this work, mathematical models of the seated human body are investigated and simulated in a Simulink/ MATLAB environment. In addition, segments of the human body are studied and models are developed and built by using Simulink/MATLAB. As part of this work, model analysis and state-space methods are used in order to check and validate the results obtained from the simulations. Two types of forces are used to test the whole seated human body under low frequency citation. The first is a sinusoidal wave signal based on literature, and the second is an impulse function. The effects of mechanical vibration on the head and lumbar are studied as these parts of the human body are usually the most effected areas. Kinematic states of the head segment and lumbar are considered. The characteristics of the vibration response on the two segments are also obtained. In addition to the mechanical vibrations study, this paper is a resource for the development and implementation of models in the Simulink/MATLAB environment.
Keywords:
Vibration, Human Body, MATLAB, State-Space

1. Introduction
Our bodies are highly sensitive to the natural activities around us. One of the most important phenomena that always affect all human body and its organisms is the vibration. Humans are sensitive to vibrations under low frequency, and the problem becomes worse when they expose to vibrations continuously [1] .
Experimental evidence has shown that a human body can be injured by vibrations. It was reported that about 12 million workers in the USA were affected by vibrations [2] . According to that, researchers have been working hard to reduce this dangerous phenomenon, and therefore they have written a lot of studies on how to avoid the effects of the vibration on the human body.
Most seated workers are exposure to vibrations effects; these effects are very harmful and in some cases lead to permanent pains, i.e. back pain. Vehicle drivers are exposed to this type of pain because they are driving their vehicle and interacting with vibration more than other people.
In order to study changes on the human body professionally, we should build a model that mimics the dynamics of the human body. For modeling the human body, it can be done by using mathematical equations derived by using one of the modeling methods, and then you can either find the analytical solutions in order to define the frequencies that have effects on the body, or use simulation software in order to build the mechanical structure of the human body and then examine it under different frequencies. In this work, several modeling methods are used to build the mathematical model of the human body in order to study the vertical vibrations on the seated human body. Then the results of these methods are compared to the results obtained from the simulated mechanical system of the human body by using MATLAB/Simulink Software.
2. Literature Review
The biodynamic study of the human body return back to 1918, when Hamilton define the vibration white finger syndrome as a result of the vibrating hand tools [2] .
Zheng, Qiu and Griffin [3] concluded that health and comfort of seated people became unsafe when the human body is exposure to low-frequency vibrations. The biodynamic responses of the seated human body to vertical vibration excitation have been measured experimentally and some of the results summarized in International Standard 5982 [4] .
There are many factors could affect the response of human bodies to the vibrations and they differ from person to another. The experimental tests in [5] - [8] summarized these factors including body weight, sitting posture, vibration magnitude, age, vibration spectra, feet, holding a steering wheel and shock or impact force applied to the human body.
Nawayseh and Griffin in [9] found that there is a fore-and-aft (cross-axis) response, evident in fore-and-aft forces at the seat and the backrest during vertical excitation in the additional to the vertical response. In [10] , the authors found that backrests could affect the response of the human body to the vibrations.
There are many biodynamic models have been built to mimic the movement of the movement of human body. According to [11] , the models of human body could be classified as lumped-parameter models, multi-body models and finite-element models. The former was the most popular model of the human body [12] [13] . The multi-body models have been based solely on the apparent mass in the direction of excitation [13] .
The objective of this work is to build two models of the human body and then study the effect of the vertical vibration on the head segment and lumbar spine using MATLAB software.
3. Measurements and Mathematical Models of Seated Human Model
3.1. Human Model
The human body is a complex dynamic system which has mechanical properties that change from person to another and from time to time. Many mathematical models have been developed on the basis of diverse field of measurements to describe the biodynamic responses of human beings [14] .
Based on different modeling methods, the human body model can be composed of lumped-parameter models. The lumped-parameter model is simple system consists of concentrated mass connected internally with springs and dampers. These models are simple construction and easier to deal with for analysis, mathematically solved and simulation.
The model used in this work is linear model as shown in Figure 1. The values of the parameters are specific constant values and are summarized in Table 1 and Table 2.
Figure 1. The human body model [14] .
Table 1. Mass values for each segment [14] .
Table 2. Damping and stiffness parameter values [14] .
3.2. Linear Graph and Bond Graph for Seated-Human Body Model
Linear and bond graphs are one of the modeling techniques used in order to find mathematical equations for mechanical skeleton. The whole system’s structure represented in linear and bond graphs are shown in Figure 2 and Figure 3, respectively.
Figure 2. Linear graph for the presented human body model.
3.3. Measurements and Mathematical Equations
The proposed seated-human body model consists of 12 degree of freedoms. In order to find the mathematical equations for each segment, free body diagram should be drawn and then Newton’s 2nd law should be applied.
The equations of a general n-degree-of-freedom system are divided into n equations of the following form:
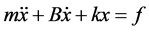
Rewrite the above equation, you will obtain:
For mass 1 (Seat)
Figure 3. Bond graph for the represented human body model.
For mass 2 (Pelvis)
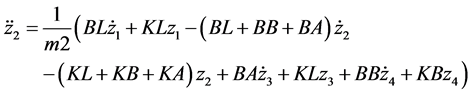
For mass 3 (Abdomen)
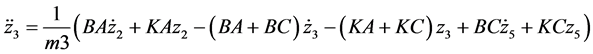
For mass 4 (Lumbar spine)

For mass 5 (Diaphragm)
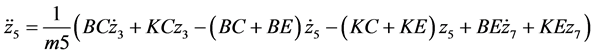
For mass 6 (Thoracic spine)
For mass 7 (Thorax)
For mass 8 (Cervical spine)
For mass 9 (Torso)
For mass 10 (Head)

For mass 11 (Upper Arm)
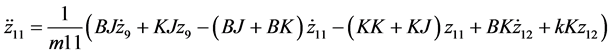
For mass 12 (Lower Arm)
4. Simulation
There are several methods to solve the n-DOF system; n equations of second order differential equation for each DOF. Solution could be achieved analytically or numerically by using one of the engineering Software. In this work, they will be solved using three techniques:
1) MATLAB/Simulink: 2 simulation models are used in order to validate results
2) Modal Analysis; this method was explained in previous section
3) State space Representation
4.1. First Simulation Model of the Mechanical Skeleton of the Human Body
The first simulation model is built to include all the mass segments of the human body together as shown in Figure 4.
Figure 4. 1st simulation model of the mechanical skeleton of the human body using Sımulınk/MATLAB.
4.2. Second Simulation Model of the Human Body Using Ordinary Differential Equations
The second simulation model of the human body is built by drawing the 2nd ODE for each mass of the body segments separately using Simulink/MATLAB as shown in Figures 5-16.
Figure 5. Simulation part for the seat segment.
Figure 6. Simulation part of the Pelvis segment.
Figure 7. Simulation part of the abdomen segment.
Figure 8. Simulation part of the lumbar spine segment.
On this work we only care about the head and lumber spine segments as they are taking the most damages. In order to find their transfer function, MATLAB’s control and estimation manager (CEM) toolbox is used. This is done by using the State Space equation and the Bode plot for each mass of the human body as shown in Figures 17-23 and as follows.
1) Select the inputs of the system.
2) Select the outputs of the system.
Figure 9. Simulation part of the diaphragm section.
Figure 10. Simulation part of the thoracic spine segment.
Figure 11. simulation part of the thorax segment.
Figure 12. Simulation part of the cervical spine segment.
3) Open the control and estimation tools manager and linearize the system in order to get the transfer function, state space equations, and other characteristics of the system.
4) Obtaining the Bode plot for the seat, head and lumbar spine segments.
5) Obtaining the transfer functions.
Figure 13. Simulation part of the torso segment.
Figure 14. Simulation part of the head segment.
Figure 15. Simulation part of the upper arm segment.
Figure 16. Simulation part of the lower arm segment.
Figure 17. Selecting the input point that will be used in the CEM toolbox.
Figure 18. Selecting the output point that will be used in CEM toolbox.
Figure 19. Selecting the system’s characteristics in CEM toolbox.
4.3. Model Analysis
Equations of motion of a multi-degree-of-freedom system under external forces are given by the following equation:
where [m], [B], [K] and [f] for our system are explained as the following;
Figure 20. The Bode plot of the seat, head and lumbar spine segments.
Figure 21. Transfer function of the seat segment.
Figure 22. Transfer function of the head segment.
Figure 23. Transfer Function of the lumbar spine segment.
Vertical input force is any input force applied on the system such as sinusoidal wave signal, step-function signal, ramp-function signal, impulse-function signal, etc. All the variables in the above equations are numerically defined and set in Table 1 and Table 2.
4.4. State-Space Representation
The State-Space method is useful for modelling multi-DOF systems. It could be used to represent the entire states of the system at any given time.
General form representation:
where A, B, C and D are the system, input, output and feed-forward matrices, and x, y and u are the state, output and input vectors.
For human body model in previous sections, the equations could be rewritten in state-space representation form in order to model the whole system. It is assumed that:
According to that, equations of the human body are as the following:
There are several methods to solve the state-space equations. In this work, the Laplace inverse method has been used in order to get the transition matrix
Then,
lsim(sys, u, t) function produces a plot of the time response of the dynamic system model sys to the input time history t, u. The vector t specifies the time samples for the simulation (in system time units, specified in the Time Unit property of sys), and consists of regularly spaced time samples.
5. Results
5.1. 1st Simulation Model Results
5.1.1. Sinusoidal Wave Input Signal
The velocity and the position for each of the head and lumber spine segments of the human body with respect to the sinusoidal wave input signal are shown in Figures 24-27, respectively.
Figure 24. Sinusoidal wave input and the corresponding head’s velocity.
Figure 25. Sinusoidal wave input and the corresponding head’s position.
Figure 26. Sinusoidal wave input and the corresponding lumber spine’s velocity.
Figure 27. Sinusoidal wave input and the corresponding lumber spine’s position.
5.1.2. Impulse-Function Input Signal
The velocity and the position for each of the head and lumber spine segments of the human body with respect to the impulse-function input signal are shown in Figures 28-31, respectively.
5.2. 2nd Simulation Model Results
5.2.1. Sinusoidal Wave Input Signal
The acceleration, velocity and position for both of the head and lumber spine segments of the human body with respect to the sinusoidal wave input signal are shown in Figures 32-37, respectively.
5.2.2. Impulse-Function Input Signal
The acceleration, velocity and the position for each of the head and lumber spine segments of the human body with respect to the impulse-function input signal are shown in Figures 38-43, respectively.
Figure 28. Impulse-function input signal and the corresponding head’s velocity.
Figure 29. Impulse-function input signal and the corresponding head’s position.
Figure 30. Impulse-function input signal and the corresponding lumber spine’s velocity.
Figure 31. Impulse-function input signal and the corresponding lumber spine’s position.
Figure 32. Sinusoidal wave input signal and the corresponding head’s acceleration.
Figure 33. Sinusoidal wave input signal and the corresponding head’s velocity.
Figure 34. Sinusoidal wave input signal and the corresponding head’s position.
Figure 35. Sinusoidal wave input signal and the corresponding lumber spine’s acceleration.
Figure 36. Sinusoidal wave input signal and the corresponding lumber spine’s velocity.
Figure 37. Sinusoidal wave input signal and the corresponding lumber spine’s position.
Figure 38. Impulse-function input signal and the corresponding head’s acceleration.
Figure 39. Impulse-function input signal and the corresponding head’s velocity.
Figure 40. Impulse-function input signal and the corresponding head’s position.
Figure 41. Impulse-function input signal and the corresponding lumbar spine’s acceleration.
Figure 42. Impulse-function input signal and the corresponding lumbar spine’s velocity.
5.3. State-Space Method Results
5.3.1. Sinusoidal Wave Input Signal
The velocity and position for both of the head and lumber spine segments of the human body with respect to the sinusoidal wave input signal are shown in Figures 44-47, respectively.
5.3.2. Impulse-Function Input Signal
The velocity and the position for each of the head and lumber spine segments of the human body with respect to the impulse-function input signal are shown in Figures 48-51, respectively.
6. Discussion and Conclusion
6.1. Discussion
Figure 20 represents the transfer function (gain and phase shift) of the human segments
Figure 43. Impulse-function input signal and the corresponding lumbar spine’s position.
Figure 44. Sinusoidal wave input signal and the corresponding head’s velocity.
Figure 45. Sinusoidal wave input signal and the corresponding head’s position.
Figure 46. Sinusoidal wave input signal and the corresponding lumbar spine’s velocity.
Figure 47. Sinusoidal wave input signal and the corresponding lumbar spine’s position.
Figure 48. Impulse response of the head’s velocity.
Figure 49. Impulse response of the head’s displacement.
Figure 50. Impulse response of the lumber spine’s velocity.
Figure 51. Impulse response of the lumber spine’s displacement.
(seat, head and lumber spin) subjected to vertical sinusoidal force with amplitude of 15 N. Head and lumbar spine segments are most segments that suffer from the vibration.
The gain represents the amplitude ration between the output and input inertia. Positive gain indicates that the 

Resonance can cause large oscillation when the frequency of excitation coincides with the natural frequency of the relevant subject. Harmful mechanical effect of vibration occurs because of induced strain on different tissues, caused by motion and deformation within the body.
The mechanical energy due to vibration is absorbed by tissues and organs, when the vibrations are attenuated in the relevant body segment. Consequently, vibration leads to muscle contractions (Voluntary and involuntary) which can cause local muscle fatigue, particularly when the body vibrated at the resonant frequency level.
6.2. Conclusion
Two simulation models have been designed to represent the human body subjected to vertical vibration by using mechanical parameters obtained from [15] . Simulink/ MATLAB software has been used to develop and implement the models obtained using the model analysis and state-space methods. The results from these two approaches confirm that the head and lumbar suffer the most from vibration in terms of forces. In addition, it is found that the rest of the organs may become strained leading to pain and fatigue, depending on the magnitude of the vibrations.
Cite this paper
AlShabi, M., Araydah, W., ElShatarat, H., Othman, M., Younis, M.B. and Gadsden, S.A. (2016) Effect of Mechanical Vibrations on Human Body. World Journal of Mechanics, 6, 273- 304. http://dx.doi.org/10.4236/wjm.2016.69022
References
- 1. Amirouche, F.M.L. (1987) Modeling of Human Reactions to Whole-Body Vibration. Journal of Biomechanical Engineering, 109, 210-217.
http://dx.doi.org/10.1115/1.3138671 - 2. Hamilton, A. (1918) Reports of Physicians for the Bureau of Labor Statistics—A Study of Spastic Anemia in the Hands of Stone Cutters. Bulletin 236, Industrial Accidents and Hygiene National Technical Information Services (NTIS PB-254601), 53-66.
- 3. Zheng, G., Qiu, Y. and Griffin, M.J. (2011) An Analytic Model of the In-Line and Cross-Axis Apparent Mass of the Seated Human Body Exposed to Vertical Vibration with and without a Backrest. Journal of Sound and Vibration, 330, 6509-6525.
http://dx.doi.org/10.1016/j.jsv.2011.06.026 - 4. International Organization for Standardization ISO 5982 (2001) Mechanical Vibration and Shock-Range of Idealized Values to Characterize Seated-Body, Biodynamic Response under Vertical Vibration. International Standard.
- 5. Fairley, T.E. and Griffin, M.J. (1989) The Apparent Mass of the Seated Human Body: Vertical Vibration. Journal of Biomechanics, 22, 81-94.
http://dx.doi.org/10.1016/0021-9290(89)90031-6 - 6. Toward, M.G.R. (2002) Apparent Mass of the Human Body in the Vertical Direction: Effect of Input Spectra. Proceedings of the 37th United Kingdom Group Meeting on Human Responses to Vibration, Department of Human Sciences, Loughborough University, Loughborough, 18-20 September 2002, 67-75.
- 7. Nawayseh, N. and Griffin, M.J. (2004) Tri-Axial Forces at the Seat and Backrest during Whole-Body Vertical Vibration. Journal of Sound and Vibration, 277, 309-326.
http://dx.doi.org/10.1016/j.jsv.2003.09.048 - 8. Toward, M.G.R. and Griffin, M.J. (2010) Apparent Mass of the Human Body in the Vertical Direction: Effect of a Footrest and a Steering Wheel. Journal of Sound and Vibration, 329, 1586-1596.
http://dx.doi.org/10.1016/j.jsv.2009.11.015 - 9. Fairley, T.E. and Griffin, M.J. (1990) The Apparent Mass of the Seated Human Body in the Fore-and-Aft and Lateral Direction. Journal of Sound and Vibration, 139, 299-306.
http://dx.doi.org/10.1016/0022-460X(90)90890-C - 10. Wei, L. and Griffin, M.J. (1998) Mathematical Models of Apparent Mass of Seated Human Body Seated to Vertical Vibration. Journal of Sound and Vibration, 21, 855-874.
http://dx.doi.org/10.1006/jsvi.1997.1473 - 11. Matsumoto, Y. and Griffin, M.J. (2001) Modelling the Dynamic Mechanisms Associated with the Principal Resonance of the Seated Human Body. Clinical Biomechanics, 16, 31-44.
http://dx.doi.org/10.1016/S0268-0033(00)00099-1 - 12. Nawayseh, N. and Griffin, M.J. (2009) A Model of the Vertical Apparent Mass and the Fore-and-Aft Cross-Axis Apparent Mass of the Human Body during Vertical Whole-Body Vibration. Journal of Sound and Vibration, 319, 719-730.
http://dx.doi.org/10.1016/j.jsv.2008.05.030 - 13. Qiu, Y. and Griffin, M.J. (2010) Modelling the Fore-and-Aft Apparent Mass of the Human Body and the Transmissibility of Seat Backrests. Vehicle System Dynamics, 49, 1-20.
- 14. Qassem, W., Othman, M.O. and Abdul-Majeed, S. (1994) The Effects of Vertical and Horizontal Vibrations on the Human Body. Medical Engineering & Physics, 16, 151-161.
http://dx.doi.org/10.1016/1350-4533(94)90028-0 - 15. Rao, S.S. (2006) Mechanical Vibration. 5th Edition, Pearson Education, Inc., Upper Saddle River, 603-606.


















































































