Received 31 March 2015; accepted 10 May 2015; published 13 May 2015

ABSTRACT

The paper presents a quaternion approach of giving a closed form solution of the motion in a cen- tral force field relative to a rotating reference frame. This new method involves two quaternion operators: the first one transforms the motion from a non-inertial reference frame to a inertial one with a very significant consequence of vanishing all the non-inertial terms (Coriolis and cen- tripetal forces); the second quaternion operator provides the solution of the motion in the non- inertial reference frame by applying it to the solution in the inertial reference frame. This process will govern the inverse transformation of the motion and is proved on two particular cases, the Foucault Pendulum and Keplerian motions problems relative to rotating reference frames.

Keywords:

Quaternion, Rotating Reference Frame, Foucault Pendulum Motion, Keplerian Motion

1. Introduction

The present paper presents a quaternion solution of the motion in a central force field relative to a rotating ref- erence frame. It starts from the main Cauchy problem stated below:

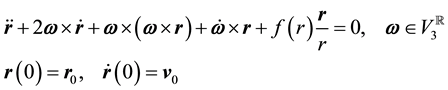(1.1)

where 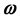is a differentiable vectorial map and 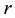is the magnitude of vector.

The quaternion method which will be presented in this paper involves two quaternion operators from which the first one transforms the non-linear with variable coefficients initial value problem (1.1) in another one without the coefficients and the second quaternion operator, applied to the solution of the last problem, will provide the time-explicit closed form solutions for two specific cases, Foucault Pendulum and Keplerian motion problem when 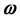has a fixed direction.

The structure of this paper consists of the following four parts. Section 2 starts with a brief presentation of the quaternion algebra and continues with the presentation of Darboux problem in quaternion form in order to prepare the defining of the quaternion operators.

The next section represents the core of the paper because there the quaternion operators are defined, but not before the transformation in the quaternion form of the Equation (1.1) to be done.

Section 4 proves the accuracy of the method of using quaternion operators for computing the time-explicit closed form solutions for two particular cases, the Foucault Pendulum and Keplerian motions problems in rotating reference frame.

2. Mathematical Preliminaries

2.1. Algebra of Quaternions

The quaternions were invented by William Rowan Hamilton in 1843 [1] . A quaternion can be written as a linear combination:

(2.1)

where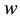, , 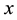, 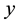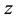are the constituents of the quaternion and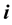, , are the imaginary units. The multiplication of two quaternions satisfies the fundamental rules introduced by Hamilton:

(2.2)

For the quaternion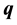, 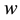is the first constituent and it’s named “the real part” and x, y, z form the vector part of the same quaternion. We can use the quaternions when we need to model rotations, especially in the case of the motion of the rigid body around a fixed point. A quaternion can also be noted as:

(2.3)

where is a real number and is a vector. In this case, is named the real part of and is the vector part of. A quaternion with zero real part called vector quaternion.

The set of quaternions is denoted by and is a noncommutative; associative four dimensional division algebra with respect to the scalar multiplication, quaternion sum and quaternion product, defined as:

(2.4)

with being the vector dot product and representing the vector cross product.

We already know that an algebra is a vector space where the product may be defined as an additional internal operation. Also, the dimension of an algebra is the algebraic dimension of the vector space. We will define a division algebra as an algebra where the division operation is possible. So, for any and, with, there are two unique elements and in the algebra, as:

(2.5)

We will denote with the conjugate of the quaternion from (2.3), the conjugate being defined as . The norm of the quaternion is given by:

(2.6)

when is the magnitude of vector. We will denote with and two vectors and their corresponding vector quaternion form. We also know that the vector dot product and cross product may be expressed in a quaternion way as below:

(2.7)

We can describe the motion of a particle on a sphere with a constant radius with the help of time-depending quaternions such as:

(2.8)

where is the vector quaternion that models the motion, is a constant vector quaternion and is a time-depending quaternion with. The next equation will describe the finite rotation with an angle of the vector around the axis whose orientation is modeled by the vector quaternion with:

(2.9)

where has the form as:

(2.10)

2.2. Darboux Equation in Quaternion Shape

It is well known that in rigid body kinematics, we need to describe the instantaneous rotation when we know the angular velocity [2] . The common solution is to use the Riccati differential equation which describes the instantaneous rotation of a rigid body when the instantaneous angular velocity is given [3] .

If R is the rotation matrix, the rotation with angular velocity of a constant vector is described by [4]

(2.11)

If a vector is represented in Cartesian coordinates with respect to the orthonormal right oriented basis,

(2.12)

and if the matrix is related to the vector as below

(2.13)

the instantaneous angular velocity vector associated to the proper orthogonal valued function is defined by

(2.14)

The rotation matrix that models the rotation with a given instantaneous angular velocity is given by the solution to the Darboux equation represented below in the matrix shape:

(2.15)

where is the initial moment of time and is a matrix whose elements are differentiable scalar functions.

The rotation matrix associated with vector is the solution of the initial value problem (2.15) and it is a proper orthogonal matrix function with the following properties:

(2.16)

Consider the vector quaternion corresponding to the instantaneous angular velocity vector and the unit quaternion that models the rotation. The quaternion operator defined as below rotates any constant vector with instantaneous angular velocity.

(2.17)

From Equation (2.14), it results that:

(2.18)

and using vector quaternions property (2.7) we will rewrite (2.18) as

(2.19)

Due to the fact that is an arbitrary constant vector quaternion, from (2.19) results that the unit quaternion, which describes the rotation with angular velocity, is the solution to the following Darboux-like equation:

(2.20)

where is a unit quaternion. In this case, from Equation (2.15), is the vector quaternion associated with vector.

Using (2.15) and the expression of from (2.17), it follows that the continuous rotation with instantaneous angular velocity modeled by the vector quaternion is the solution to the quaternion initial value problem:

(2.21)

3. The Solutions of the Motion in a Central Force Field Relative to a Rotating Reference Frame

In order to find the solutions of the equations specific to the motions in a central force field relative to a rotating reference frame, two reciprocal transformations will be done: first, the motion in the non-inertial reference frame will be transformed in a inertial one through the quaternion operator. Then will be proved that the solution of the equation specific to the non-inertial reference frame results very easy by applying the quaternion operator to the solution specific to the inertial reference frame where.

Quaternionic Operator

In this section, a quaternion operator will be defined in order to determine the solution of the below non- linear initial value problem which describes the motion in a central force field relative to a rotating reference frame. The first step is to recall the Cauchy problem specific to the motion in a central force field:

(3.1)

Knowing that is a differentiable vectorial value map, is the magnitude of vector, and is a continous real valued map. Using (2.7), the last equation becomes:

(3.2)

and further,

(3.3)

Now, the following quaternion operator is defined as:

(3.4)

where is the solution of the following equation:

(3.5)

If, then the Equations (3.4) and (3.5) determines the following properties:

1. For any quaternions and and scalars and, the operator is linear, i.e.:

(3.6)

2. For any quaternions and, the operator preserves the quaternionic product i.e.

(3.7)

3. For any quaternion, the operator preserves the quaternionic norm i.e.

(3.8)

4. If is a quaternion-valued function of a real variable, the derivative with respect to time of is:

(3.9)

5. If is a quaternion-valued function of a real variable, the second derivative with respect to time of is:

(3.10)

6. is invertible and it’s inverse is denoted with i.e.:

(3.11)

where describes the rotation with the angular velocity which corresponds to the vector quaternion and is the solution of Equation (3.5).

Theorem 3.1.

The solution of the Cauchy problem:

(3.12)

will be obtained by applying the quaternion operator, to the solution of the Cauchy problem:

(3.13)

Proof. If we apply to the Equation (3.3), it results:

(3.14)

Using the Equation (3.10), it results that:

(3.15)

Replacing with and using the Equation (3.11), it results:

(3.16)

Consequently, by using the quaternion operator, the complex problem given by the non-linear initial value problem with variable coefficients described by Equation (3.1) is reduced to the finding the solution of Equation (3.16) which describes the motion in a central force field, with being the instantaneous angular velocity of the rotating reference frame. Thereby, the movement in the non-inertial reference frame is trans- formed to an inertial one and all non-inertial coefficients within Equation (3.1) are canceled. The solution of Equation (3.1) will be obtained by applying the quaternion operator, to the solution of the problem (3.16).

In the next sections will be studied two particular cases of motions in central force field: the Foucault Pendulum and the Kepler’s motions relative to a rotating reference frame problems.

4. Study of Particular Cases: Foucault Pendulum and Keplerian Motion Problems in Rotating Reference Frames

This section presents the methods adequate to the very known two topics: the Foucault Pendulum and Keplerian motion problems relative to a rotating reference frame problems. In order to achieve the goal of this paper, the motion in central force field Equation (1.1) will be particularized for these two specific cases giving for each of them the characteristic eqaution of and the quaternion operator, will be used as presented in last section.

4.1. Foucault Pendulum Problem

The Foucault Pendulum motion is described by the below initial value problem which is a particular form of the Equation (1.1) that coresponds to a spatial harmonic oscillator relative to a rotating reference frame, with

,

(4.1)

where is the position vector, represents the angular velocity of the rotating reference frame and is a diferential vectorial map and at last but not the least important, is the pulsation of the pendulum which depends on both the gravitational acceleration at the place of the experiment and the length of the pendulum.

Applying the quaternion operator, the Equation (4.1), we will produce the below initial value problem:

(4.2)

The Equation (4.2) models the spatial harmonic oscillator and it’s solution is:

(4.3)

Due to the Theorem 3.1., the solution of the initial value problem

(4.4)

results from applying the the quaternion operator to the solution (4.3) of the Cauchy problem (4.2) as below:

(4.5)

The solution of Equation (4.5) coresponds to a harmonic planar oscillation (with being the pulsation of the pendulum) composed with a precession of angular velocity of the oscillation plane [5] .

In order to compute the closed form solutions of Equation (4.1), we must recall that we’ve assumed that the direction of the vector associated with the quaternion is considered to be fixed where is a constant unit vector with and, from Eqaution (3.11), that the quaternion operator . Consequently,

(4.6)

with.

If we’ll note:

(4.7)

than the Equation (4.6) can be rewritten as following:

(4.8)

In conclusion, when the direction of the vector associated with the quaternion ω is considered to be fixed, the motion is a harmonic oscillation described by the Equation (4.3) in a plane that has a fixed point and a pre- cession with the angular velocity.

4.2. Kepler’s Problem in Rotating Reference Frame

The Keplerian motion in a rotating reference frame that rotates with the angular velocity is described by the

following linear initial value problem which is a particular form of the Equation (3.1) with

(4.9)

where is the position vector of the body related to the attraction center, represents the angular velocity of the rotating reference frame and is a differential vectorial map and is a constant with μ = kM where k is the universal attraction constant and M is the mass of the attraction center.

It was proved in the second section that the solution to the Cauchy problem is obtained by applying the quaternion operator to the solution of the following Cauchy problem:

(4.10)

The Equation (4.10) describes a typical Keplerian motionunder certain conditions.

In the particular case of negative specific energy, the solution of (4.11) is: [6] [7]

(4.11)

where

In the Equation (4.11), the coefficients and are the vectorial semimajor and, respectively, the semi- minor axes of the elliptical inertial trajectory, is the vectorial eccentricity of the trajectory with being its magnitude and constant is named mean motion as below:

(4.12)

where the specific energy is noted with and is equal with:

(4.13)

and the specific angular momentum of the inertial trajectory is noted with and equal to:

(4.14)

The eccentricity of the trajectory is given by:

(4.15)

with

(4.16)

and the mean motion is:

(4.17)

where. (4.18)

The function is the eccentric anomaly defined by:

(4.19)

with given by:

(4.20)

Now, in order to find the solution to the Cuchy problem ( 4.21), the quaternion operator has to be applied to the solution of the Equation (4.11) resulting:

(4.22)

Using the properties of the quaternion operator, Equation (4.22) becomes:

(4.23)

Again, the direction of the vector associated with the quaternion is considered to be fixed where is a constant unit vector with and, from Eqaution (3.11), the quater- nion operator transforms the Equation (4.23) as below:

(4.24)

with.

Consequenly, similar to the Foucault pendulum case, the Keplerian motion relative to a rotating reference frame consists of two motions: a Keplerian elliptical motion described by the Equation (4.11) and a rotation with the angular velocity.

5. Conclusion

The quaternion method described in this work presents a new perspective to the clasical problem of motion in central force field relative to the rotating reference frames and provides us a very powerfull tool to solve the similar problems. Throughout the paper, two quaternion operators are defined in order to reveal the closed form solution to the two particular problems of the Foucault Pendulum and Keplerian motions in rotating reference frame.

References