World Journal of Mechanics
Vol.05 No.03(2015), Article ID:54677,8 pages
10.4236/wjm.2015.53004
Viscosity Transient Phenomenon during Drop Impact Testing and Its Simple Dynamics Model
Chen Liu, Yoshikazu Tanaka, Yukio Fujimoto
Department of Transportation and Environmental Engineering, Graduate School of Engineering Science, Hiroshima University, Higashi-Hiroshima, Japan
Email: fujimoto@naoe.hiroshima-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 February 2015; accepted 13 March 2015; published 16 March 2015
ABSTRACT
Most soft materials behave as if they were hardened when subjected to an impact force. The strain rate dependence of viscosity resistance is the reason for this behavior. The authors carried out drop impact tests on several types of soft materials under the condition of a flat frontal impact. The impact force waveform of soft materials was found to consist of a thorn-shaped waveform and a succeeding mountain-shaped waveform. Based on our experimental observations, we believe that a large viscosity resistance is rapidly changed to a small resistance in the course of the impact. In the present study, the cause of this distinct waveform is discussed based on a dynamics model. The study applies a standard linear solid (SLS) model in which the viscosity transient phenomenon is considered is applied. Three types of impact force waveforms of actual soft materials are simulated using the SLS model. Some features of the impact force waveform of soft materials can be explained using the SLS model.
Keywords:
Impact Force, Soft Material, Standard Linear Solid Model, Viscosity Transient, Strain Rate Dependence

1. Introduction
Most soft materials have the properties of both viscosity and elasticity. Elastic properties are only slightly affected by the strain rate dependence. On the other hand, viscosity properties (including plastic deformation) are strongly affected by the strain rate dependence. A soft material with a strong viscosity resistance behaves as if it were hardened under a fast load, such as an impact load. For example, in a static state, agar jelly is softer than rubber. However, its impact force waveform has a shorter impact period than that of rubber.
In order to observe the features of impact force waveforms of soft materials, we conducted drop impact experiments for several types of soft materials [1] . The examined materials are agar jelly, sponge, sponge rubber, nitrile rubber, oil clay, paper clay, low-rebound urethane foam, ham, eligible meat, konjac, and cork. The experiments were carried out under a flat frontal impact condition.
The experiments reveal that the impact force waveform of a soft material consists of a thorn-shaped waveform, followed by a mountain-shaped waveform. The thorn-shaped waveform is a spike-like waveform, which is observed in the rising segment of the waveform. This type of thorn-shaped waveform appears in all the results for all of the soft materials except cork sheet. The existence of the thorn-shaped (spike-like) waveform is also reported in a previous study based on a Kolsky bar experiment [2] .
From the experimental observations, we believe that the thorn-shaped waveform is caused primarily by the viscosity resistance, and the mountain-shaped waveform is caused primarily by the elastic resistance. In other words, a transient occurs from the viscosity-dominant waveform to the elasticity-dominant waveform during the impact period.
In the present study, we attempt to simulate the impact force waveforms of soft materials by applying a dynamics model considering the viscosity transient mechanism. The standard linear solid (SLS) model is used in the simulation [3] [4] . The soft material is modeled as a combination of a spring and a dashpot. The viscosity transient is defined by the rapid change in viscosity resistance of the dashpot. The simulated waveforms are compared with the actual waveforms measured in the experiment.
2. Impact Force Waveform of a Soft Material
Figure 1(a) shows a soft material subjected to a flat frontal impact. The impact object is a free drop hammer. Figure 1(b) shows typical thorn-shaped waveforms of the impact force. The features of the thorn-shaped waveform include a steep slope θ on the rising segment and a thorn-shaped waveform similar to the yield point of low-carbon steel. After that, at a certain point, the slope α becomes gentler and generates a second mountain- shaped waveform. The rising segment of the thorn is usually similar to a straight line.
Figure 1(c) summarizes the occurrence mechanism of thorn-shaped waveforms obtained by the experimental observation. The impact force waveform of soft materials is a mixture of two types of waveforms. The first (thorn-shape) waveform exhibits a large viscosity resistance (red curve), and the second (mountain-shape) waveform exhibits a small viscosity resistance (dashed black curve). This resistance change occurs suddenly at the thorn peak. In other words, during the impact period, the phenomenon changes from a viscosity-dominant waveform to anelasticity-dominant waveform. The compressive stress at the thorn peak is considered as the trigger of this transient. The soft material surface is struck twice by the relative movement of collision objects. The reason is that the slope α becomes smaller than the initial slope θ because the viscosity discontinuity is induced by the first strike.
3. Condition of Flat Frontal Impact and Compact Drop Test Equipment
Through a number of experiments, we found that the thorn-shaped waveform could be clearly measured under the condition of a flat frontal impact [1] [5] . In Figure 2, the impact object is solid and has a flat contact surface. The soft material that receives the impact force is a plate-like material with a uniform thickness without surface irregularities. The impact object strikes the soft material in the normal direction. The thorn-shaped waveform can be steadily measured under the above condition. When the bottom surface of the impact object is curved (Figure 2(b)), when the impact object is tilted (Figure 2(c)), or when the upper surface of the soft material is curved (Figure 2(d)), the thorn-shaped waveform becomes unclear. Here, “unclear” does not mean that thorn- shaped waveform does not occur. Rather, the thorn-shaped waveform is not obvious in the contact area that expands gradually from the local area, and the phenomenon is diluted.
Figure 3 shows the free drop test equipment used in this study. The device is braced by vertical columns on the left and right of the bottom plate. The top of the side column is connected with a metal plate. The drop hammer is made of an aluminum circular disk plate and a stainless cylinder (mass of 1.9 kg). The contact surface of the hammer bottom is a disk plate with a diameter of D = 60 mm. The upper sensor is an orbicular pad sensor and is attached near the drop hammer bottom. The lower sensor is a pad sensor of 100 mm square and is
Figure 1. Impact force waveform of a soft material. (a) Flat frontal impact by a free drop hammer for a plate-like soft material; (b) Typical impact force waveform of a soft material including a thorn-shaped waveform; (c) Two types of waveforms contained in the impact force waveform of a soft material.
Figure 2. (a) Flat frontal impact condition for which the thorn appears clearly; (b), (c), and (d) Flat frontal impact condition for which the thorn is indistinct.
Figure 3. Drop test equipment and the upper and lower sensors used in the device.
attached to the frame bottom. Both sensors are made from piezoelectric film. A high-speed voltage recorder with a sampling rate of 20 - 200 kHz is used for recording the sensor output. The output of the upper sensor is modified by 8% to account for the mass of the disk plate.
Based on rigorous tests using a servo-controlled testing machine and a high-rigidity load cell, it was confirmed that both sensors could measure the impact force very accurately when the contact time was in the range between 0.1 msec and 2 sec. The drop height h is the height from the upper surface of the soft material to the bottom surface of the drop hammer. The impact velocity is V0 = 1.4 m/sec when h = 0.1 m, V0 = 2.73 m/sec when h = 0.38 m, and V0 = 3.13 m/sec when h = 0.5 m.
4. Examples of Measured Impact Force Waveforms
Figure 4(a) shows the impact force waveforms of a gel sheet (product name: a gel) with a T = 20 mm thickness. Figure 4(b) is an enlarged view of the thorn part. The drop height is h = 380 mm (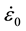 = 136 sec−1). The thorn- shape waveform can be seen clearly in both the upper and lower sensor outputs. In the enlarged view, we can observe that the slope θ of the rising segment is larger than the slope α of the segment past the thorn. The impulse of the thorn part is quite small compared with the succeeding mountain-shape waveform.
= 136 sec−1). The thorn- shape waveform can be seen clearly in both the upper and lower sensor outputs. In the enlarged view, we can observe that the slope θ of the rising segment is larger than the slope α of the segment past the thorn. The impulse of the thorn part is quite small compared with the succeeding mountain-shape waveform.
Figure 5(a) is the impact force of a nitrile rubber (NBR) plate with a T = 30 mm thickness. The drop height is h = 380 mm (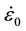 = 91 sec−1). The upper sensor output shows a relatively large thorn, and the lower sensor out-
= 91 sec−1). The upper sensor output shows a relatively large thorn, and the lower sensor out-

Figure 4. Impact force waveform induced by the hammer drop onto gel sheet with 20 mm thickness.

Figure 5. Impact force induced by the hammer drop onto NBR with T = 30 mm.
put shows a smaller thorn. The slopes θ of the upper and lower sensor outputs are almost the same. Figure 5(b) compares the impact force waveforms of the upper sensor for drop heights of h = 100, 200, and 380 mm. In the figure, when the impact velocity V0 is faster, the slope θ of the rising segment and the height of the thorn peak are larger. This means that the slope θ and the height of the thorn peak are dependent on the impact velocity or strain rate.
Figure 6 shows the impact force waveform of an oil clay plate with a T = 50 mm thickness. The drop height is h = 100 and 530 mm. A large thorn is seen by the upper sensor, and a small thorn is seen by the lower sensor. As the drop height increases (V0 becomes faster), the slope θ becomes larger, and the thorn peak becomes taller. The thorns are more obvious than those of other materials. From the enlarged view, the thorn shape is close to an isosceles triangle.
5. Viscosity Transient Phenomenon of a Soft Material under the Drop Test
In the drop impact experiment, strain rate varies with time. The strain rate is large at the beginning of the collision. The strain rate is reduced with the compression of the material and becomes zero at the time of maximum compression.
Therefore, the strain rate dependency of the material changes at every moment during the impact. If it is assumed that the viscosity resistance decreases gradually along with the decrease of the strain rate, the thorn- shaped waveform will not be generated. From the experimental observations, however, we believe that the viscosity resistance changes rapidly or discontinuously (viscosity transient) in the course of the collision process.
Figure 7 shows a schematic diagram of the relationship between the viscosity resistance and the strain rate. We believe that two phases of viscosity resistance appear in the impact force results for soft materials. One phase is an excessively large viscosity resistance (red curve), which appears at the first stage, and the other phase is a small viscosity resistance (black dashed curve), which appears in the second stage. This viscosity transient (green dashed arrow) occurs at the peak of the thorn.
Figure 6. Impact force induced by the hammer drop onto oil clay with 50 mm thickness.
Figure 7. Viscosity resistance vs. strain rate relationship.
In the case of some colloidal suspensions, the viscosity changes rapidly at a certain shear rate. This phenomenon is known as the viscosity discontinuity [6] . This discontinuity also occurs under a reversible load [7] . Based on the experimental observations, we believe that this viscosity discontinuity phenomenon also occurs in most soft materials (soft solids). The impact force waveform of the soft material takes on a distinctive shape as a result of the viscosity discontinuity. In the next chapter, the impact force waveform is simulated considering the viscosity transient.
6. Simulation of the Impact Force Waveform by the Voigt Model and the Standard Linear Solid (SLS) Model
Figure 8 shows the condition under which the drop hammer (mass: m = 1.9 kg) collides with the plate-like soft material at a speed V0. The thickness of the soft material is T. The soft material is modeled by the Voigt model or the SLS model. The mass (drop hammer) is not connected to the spring and dashpot. The Voigt model can be represented by a viscous damper c and an elastic spring k1 connected in parallel, as shown in the figure. The SLS model adds an elastic spring k1 to the Maxwell model (c, k2) in parallel. The impact velocity V0 = 2.73 m/s, which corresponds to the drop height h = 0.38 m of the hammer, is given to the mass as the initial condition. The differential equation of the SLS model is given as Equation (1), where x2 is the displacement of the hammer position, and x1 is the displacement of the dashpot. The initial strain rate is 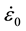 = V0/T (s−1). The Runge-Kutta method is used for solving the equation of motion.
= V0/T (s−1). The Runge-Kutta method is used for solving the equation of motion.
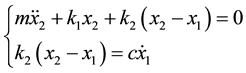 (1)
(1)
First, an analysis is carried out using the Voigt model. The spring coefficient k1 is assumed to be k1 = 1000 kN/m, which is constant throughout the collision. As mentioned above, we believe that the viscosity transient occurs in the early stage of the impact force. This influence is taken into consideration through the damping coefficient c of the dashpot. Figure 9 shows the assumed c as a time-dependent value. Here, c is c = 500 kg/s (0 < t < 0.3 ms). Then, c decreases linearly (0.3 < t < 0.4 ms), and finally becomes c = 200 kg/s (t > 0.4 ms).
Figure 10 shows the impact force waveform calculated by the Voigt model. The impact force waveform rises vertically at the beginning of the impact due to the damping coefficient of the dashpot. Although the thorn-
Figure 8. Voigt model and standard linear solid model for the simulation of the impact force waveform of a soft material.
Figure 9. Damping coefficient c assumed in the Voigt model and the standard linear solid model.
Figure 10. Impact force waveform simulated using the Voigt model.
shaped waveform caused by the viscosity transient appears, the thorn-shaped waveform is different from the measured waveform.
Next, an analysis using the SLS model is carried out. Here, k1 and c are the same as the values used in the above mentioned Voigt model. The value of k2 is assumed to be 5000 kN/m. Figure 11 shows the impact force waveform calculated by the SLS model. By placing the spring k2 in series with the damper, a small thorn-shaped waveform similar to that measured in the experiment is generated. From this figure, the SLS model is considered to be effective in the simulation of the thorn-shaped waveform.
Several types of thorn-shaped waveform are calculated using the SLS model. Figure 12 shows the impact force waveforms calculated using the SLS model for the three cases listed in Table 1. The values of k2 and c in the table are the same for these three cases, and only k1 is changed. The figure shows that the impact period becomes longer as k1 is reduced.
Figure 11. Impact force waveform simulated using the standard linear solid model.
Figure 12. Impact force waveforms calculated using the standard linear solid model.
Table 1. Spring coefficients k1, k2 and damping coefficient c for the three cases calculated.
7. Simulation of Impact Force Waveforms of Actual Soft Materials
The SLS model is applied to the simulation of the impact force waveform of actual soft materials. Nitrile rubber is chosen as the materials for the simulation. The simulation is conducted using several values of k1, k2, and c in order to determine the condition in which the calculated waveform becomes close to the experimental waveform of the respective material. In other words, k1, k2, and c are decided such that the thorn height, the mountain height, and the total impact period of the simulated waveform match those of the experimental waveform.
Figure 13 shows the impact force waveforms of nitrile rubber simulated using the SLS model. The spring coefficients k1 and k2 are assumed to be constant during the impact period, and are assumed to be k1 = 1000 kN/m and k2 = 3000 kN/m. The damping coefficient c of the dashpot is assumed to be a time dependent value, which changes during the impact period. Figure 14 shows the time variation of c. c = 1500 kg/s when 0 < t < 0.2 ms. During the period of 0.2 < t < 0.4 ms, c decreases linearly from 1500 kg/s to 100 kg/s. During the period of t > 0.4 ms, c = 100 kg/s. The period 0.2 < t < 0.4 ms is the period of the viscosity transient. A thorn shape is clearly observed in the rising segment of the waveform in Figure 14. The peak height of the thorn, the peak
Figure 13. Impact force waveform of nitrile rubber simulated using the standard linear solid model.
Figure 14. Damping coefficient c assumed for nitrile rubber.
height of the mountain-shaped waveform, and the total impact period are approximately the same as those of nitrile rubber, as shown in Figure 13.
8. Conclusions
When an impact test on soft material is carried out under the condition of a flat frontal impact, an impact force waveform consisting of a thorn-shaped waveform and a subsequent mountain-shaped waveform is obtained. We believe that this distinctive waveform is a result of the viscosity transient during the impact period. In this study, we attempt to simulate the impact force waveforms using a dynamics model. The obtained results are as follows.
1) When a soft material receives an impact force, a large viscous resistance is induced at the beginning of the impact. The viscous resistance then decreases rapidly with time. This viscosity transient phenomenon is thought to be the reason for the occurrence of the thorn-shaped waveform.
2) The standard linear solid (SLS) model can qualitatively explain the feature of the impact force waveforms of soft materials. In the SLS model, the occurrence mechanism of the thorn-shaped waveform is explained by treating the damping coefficient of dashpot as a time-dependent value.
3) A more sophisticated dynamics model is necessary in order to describe the details of the impact force waveform of the respective soft material. The densification mechanism of the material, the double-strike phenomenon, etc., should be considered in the model for the quantitative simulation.
References
- Fujimoto, Y., Liu, C., Tanaka, Y. and Shintaku, E. (2013) Measurement of Double-strike Phenomenon of Impulsive Force Using Fluctuating Load Detection Plate. Journal of the Japanese Society for Experimental Mechanics, 13, 112- 120.
- Song, B., Chen, W.W., Ge, Y. and Weerasooriya, T. (2007) Radial Inertia Effects in Kolsky Bar Testing of Extra-Soft Specimens. Experimental Mechanics, 47, 659-670. http://dx.doi.org/10.1007/s11340-006-9017-5
- Bergstorm, J.S. and Boyce, M.C. (1998) Constitutive Modeling of the Large Strain Time-dependent Behavior of Elastomers. Journal of the Mechanics and Physics of Solids, 46, 931-954. http://dx.doi.org/10.1016/S0022-5096(97)00075-6
- Roylance, D. (2001) Engineering Viscoelasticity. 1-37. http://ocw.mit.edu/courses/materials-science-and-engineering/3-11-mechanics-of-materials-fall-1999/modules/visco.pdf
- Fujimoto, Y., Liu, C., Uesugi, T., Tanaka, Y. and Shintaku, E. (2013) Pipe Surface Sensor for Impulsive Force Measurement. Transactions of the Japan Society of Mechanical Engineers Series C, 79, 1949-1959. http://dx.doi.org/10.1299/kikaic.79.1949
- Hoffman, R.L. (1972) Discontinuous and Dilatant Viscosity Behavior in Concentrated Suspensions I . Observation of a Flow Instability. Transactions of the Society of Rheology, 16, 155-173. http://dx.doi.org/10.1122/1.549250
- Bender, J. and Wagner, N. (1996) Reversible Shear Thickening in Monodisperse and Bidisperse Colloidal Dispersions. Journal of Rheology, 40, 899-915. http://dx.doi.org/10.1122/1.550767
















