Received 6 February 2015; accepted 24 February 2015; published 27 February 2015

ABSTRACT

The paper studies the motion of the Foucault Pendulum in a rotating non-inertial reference frame and provides a closed form vector solution determined by vector and matrix calculus. The solution is determined through vector and matrix calculus in both cases, for both forms of the law of motion (for the Foucault Pendulum Problem and its “Reduced Form”). A complex vector which transforms the motion equation in a first order differential equation with constant coefficients is used. Also, a novel kinematic interpretation of the Foucault Pendulum motion is given.

Keywords:

Foucault Pendulum, Non-Inertial Reference Frame, Closed Form Vector Solution, Complex Vector

1. Introduction

Swinging with elegance across the meridian of Paris inside the grand hall of the observatory, the pendulum built by Bernard Léon Foucault (1819-1868) proved the rotation of the Earth for the first time by terrestrial methods. It was a true kick for both mathematicians and physicists because none of them could write the equations or imagine this simple experiment. As we now know, Cauchy never thought that is possible that a pendulum can change the oscillation plan and Poisson said in 1827 that a pendulum cannot move such way.

The “non-mathematician” Foucault, as the members of the French Academy named him, wrote the first equation which computes the period of the whole rotation of the oscillation plan depending of the latitude of the place of oscillation. The as-known “Foucault formula” or “The law of sinus” is 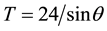(h), with 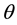being the latitude [1] [2] .

The famous experience done by Léon Foucault in 1851 emphasized the movement of the Earth around the poles, without the need for astronomical observations. The problem is very important out of the theoretical point of view. Modeling this experiment involves the study of a harmonic oscillator with respect to a non-inertial frame of reference with uniform rotation.

But finding the equation of the movement of the pendulum proved to be for mathematicians a really “hard nut” due to the non-inertial character of the reference frame. Long time, the solution had been obtained after many approximations which had to simplify the differential equations.

The type of motion that will be named “Foucault Pendulum-like motion” is described by the non-linear initial value problem [3] [4] :

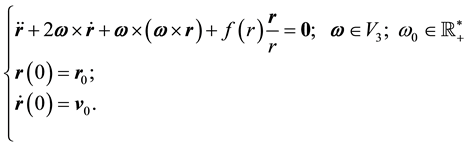( 1.1)

where 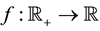is a continuous real valued map, r denotes the magnitude of vector 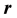and 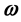is a differentiable vector value map (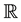denotes the set of real numbers). The above equation models the motion in a non-inertial reference frame with instantaneous angular velocity 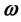in a central force field.

The motion which is described by the below linear initial value problem will be named “Foucault Pendulum motion”:

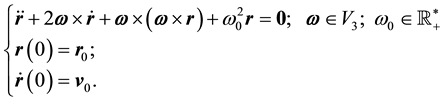. ( 1.2)

In this case, the function 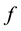from Equation (1.1) has the particular expression of a constant real number and r is the position vector, 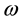is the angular velocity of the reference frame (an arbitrary differential vector map) and 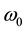is the pulsation of the pendulum which depends on its length and the gravitational acceleration at the experiment place. The relation (1.2) represents the initial value problem that describes a motion of a harmonic oscillator related to a rotating reference frame.

Many times is used the simplified form of (1.2) written below, when the inertial centripetal force is ignored (see for example [1] - [5] ):

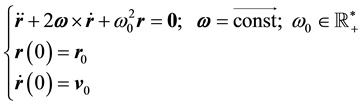( 1.3)

where 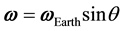is considered to be constant, 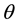is the latitude of the place of the experiment and 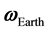represents the angular velocity of the Earth. In Equation (1.3), the inertial centripetal force is negleted and only the Coriolis forceis considered. As we know, there is no vector closed form explicit solution in any work. An approximate solution to (1.3) is given by Arnold using the isomorphism between plane vectors and complex numbers (see [5] ). In this paper, Equation (1.3) will be named Reduced Foucault Pendulum Problem and will find its vector solution in Section 5.

The present paper presents a closed form vector solution which exploits the benefits of the dualism of vector calculus and matrix calculus with extension to tensors. It is structured in five sections described below.

In the second section, two theorems which put the basis of the correspondence between vector operations and their matrix representation are stated. Two symbolic representations are defined which creates the two ways of the cross-representations of equations in vector and matrix forms.

The third section presents the vector solution of the Foucault pendulum problem (1.2) using the two symbolic representations. Here a workaround is used through a complex vector which transforms (1.2) in a first order differential equation with constant coefficients.

Section 4 prepares the next one because it presents the tensor method of representation of vector functions which will be very useful when we will find the vector solution of the Reduced Foucault Pendulum Problem (1.3). Therefore, the transformation will be defined and its properties will be listed, so that, through them, the solution of (1.3) to be found.

Finally, in Section 5, we will compute the solution of (1.3) and we will be able to extract the surprising conclusion that the solution of the Reduced Foucault Pendulum Problem is less simple than the solution of the whole Cauchy problem (1.2).

Many times, the solution to the Cauchy problem (1.3) is given only for the planar case, using polar coordinates [6] or Cartesian coordinates [7] .

2. Mathematical Preliminaries

Consider the vector space of free vectors from Euclidean space and an orthonormal basis of this space. A given vector from can be uniquely written as:

( 2.1)

Consider the vector space of column matrix, with three rows of real numbers. An element of has the following shape:

. ( 2.2)

A function

( 2.3)

is an isomorphism of vectors spaces.

If, fixed, then the function:

( 2.4)

is an endomorphism of.

If is a square matrix of order three, with real elements, fixed, non-zero, then the function:

( 2.5)

is an endomorphism on [8] .

We want to find the link between the vector and defined above as a square matrix of order three, with real elements, fixed, non-zero, for which the function (2.3) is a symbolic representation regarding the two en- domorphism and.

So, if is a rectangle orthonormal basis and:

( 2.6)

then:

. ( 2.7)

Using (2.6) and (2.7) we have:

. ( 2.8)

Therefore, with the notation:

( 2.9)

from (2.8) results the relation:

. ( 2.10)

with and from (2.6) and (2.9), respectively, we have:

Theorem 2.1. The function; defined by is an isomorphism of vectors spaces with the property:

, fixed. ( 2.11)

So, it is an exact symbolic representation, with respect to the endomorphism (2.4) of vector space over vector space with the operator (2.9).

Note: The matrix is a matrix representation of a skew-symmetric second order tensor associated with the vector (2.6) in the basis. We’ll note.

The characteristic polynomial of the skew-symmetric matrix (2.9) is:

. ( 2.12)

Solutions (roots) of the equation are:, ,.

Using one of the known proceedings for determination of an exponential matrix, it follows that:

Theorem 2.2. If and, then

( 2.13)

where,:

( 2.14)

Note: due to the Cayley-Hamilton theorem, any square matrix verifies her characteristic equation; consequently, from Equation (2.12), it follows that:

. ( 2.15)

If we denote by the inverse of the relation (2.11), we obtain, with (2.6) and (2.9), putting:

; ( 2.16)

; ( 2.17)

. ( 2.18)

If we denote by the set of vector functions of the real variable and by the set of matrix functions, with three rows and a column, of the real variable, symbolic representation (2.11) induce:

( 2.19)

fixed. ( 2.20)

3. Short Solution of Foucault Pendulum Problem

The mathematical model of this experiment is given by the Cauchy problem:

( 3.1)

In Equation (3.1), is the position vector of the particle which corresponds to the relative equilibrium position, angular velocity of the Earth, the feature pulsation of the oscillator [9] .

Using the symbolic representation, we will find a vector exact solution for the problem (3.1). Applying to the problem (3.1) the correspondence (2.11), we will obtain the matrix form:

. ( 3.2)

We will consider now the column matrix with complex functions elements given by:

( 3.3)

First, we will differentiate this column matrix:

( 3.4)

Replacing in (3.4) from (3.2) and adding and subtracting, we will obtain:

( 3.5)

After developing, (3.5) becomes

( 3.6)

Grouping the terms, (3.6) becomes:

( 3.7)

and this means that

( 3.8)

We will note with and knowing that;, (3.8) becomes:

. ( 3.9)

It results that the function is the solution of the following Cauchy problem:

. ( 3.10)

and the solution of the problem (3.10) is:

. ( 3.11)

Using Equation (3.3), and knowing that with z₁ and z₂ complex numbers, it follows that the solution of the problem (3.2) is the real part of Equation (3.11):

. ( 3.12)

Using Theorem 2.2 and the definition of a matrix exponential, it follows:

. ( 3.13)

with (3.3) and (3.13), Equation (3.12) becomes:

. ( 3.14)

After restructuring, Equation (3.14) looks like:

. ( 3.15)

with the notation:

( 3.16)

Equation (3.15) becomes:

. ( 3.17)

Applying to Equation (3.17), the correspondence, using the results of Theorem 2.2, we will obtain the vector solution of the problem (3.1):

( 3.18)

where:

( 3.19)

After elementary transformation, the solution (3.18) of the Cauchy problem (3.1) it will be written:

( 3.20)

Note:

1) The function (3.19) is the solution of the Cauchy problem:

( 3.21)

The differential equation of the problem (3.21) can be found from the differential equation of the Cauchy problem (3.1) for.

2) The solution (3.20) is the vector form of an equation matrix (3.17). This has special significance.

Let be the matrix function given by:

. ( 3.22)

The function from (3.22) is the orthogonal matrix for any. Indeed, because the matrix is skew-symmetric, we will have:

. ( 3.23)

Because from Equation (3.22), we have, , the transformation given by Equa- tion (3.17) is an own rotation for.

The angular velocity corresponding to this rotation is:

( 3.24)

The transformation (3.17) is therefore an own rotation with angular velocity. We will note with the tensor operator that matrix transcription is given by Equation (3.17). The solution for the Cauchy problem (3.1) is now written:

. ( 3.25)

with the above observation, we can obtain the next theorem:

Theorem 3.1. The solution of the Cauchy problem

( 3.26)

will be obtained applying the tensor of the rotation operator with the angular velocity:

( 3.27)

to the solution of the next Cauchy problem:

( 3.28)

Note: The hodograph of the solution of the problem (3.21) is an ellipse, possibly degenerate, having the conjugated diameters with directions given by the vectors and.

The solution of the problem (3.1) can be viewed by the rotation of the plane of the ellipse, with the angular velocity. As a rule, the hodograph of the vector function?solution of a Cauchy problem (3.1)?is a space curve.

The tensor relation (3.25) suggests a direction to approach the symbolic representation of a vector function of real variable which will be developed in the next paragraph.

4. The Symbolic Tensor Representation of a Vector Functions

This section describes the tensor method of representation the vector functions which will be used in the next chapter when we will give the solution to the Reduced Foucault Pendulum Problem.

We will denote by the orthogonal group of second order tensors (rotation tensors), by the set of the maps defined on with values in, by the group of skew-symmetric second order tensors and by the set of maps defined on with values in.

Let be the set of vector function of real variable and let be a constant.

Let be a second order skew-symmetric tensor corresponding to with. We consider, in the set of second order tensors, a first order Cauchy problem:

(4.1)

The problem (4.1) has a unique solution, if, is a continual skew-symmetric ten- sor function, the solution tensor being orthogonal, proper.

Indeed, be a tensor function of a real variable:

( 4.2)

Using Equation (4.1), it follows that verify the Cauchy problem:

( 4.3)

The solution of the problem (4.3) is unique and because the identity tensor verifies the Equation (4.3), it follows that, , therefore the solution of the problem (4.1) has the property, and is an orthogonal tensor. Knowing that and, it follows that, so is a proper orthogonal tensor.

Let

. ( 4.4)

The unique solution of Equation (4.1) will be further named as “the rotation tensor corresponding to the angular velocity”.

If is a differentiable vector function on the range, we can define the transformation as below:

( 4.5)

where is the tensor function of the unique solution of Equation (4.1).

If the vector function has fixed direction:

( 4.6)

where is a constant vector and is a real function of a real variable, the corresponding tensor function has the property of auto-commutativity:

. ( 4.7)

In this condition, the solution of the Cauchy problem (4.1) will be written in explicit form:

( 4.8)

Using one of the known procedures to determine the exponential matrix, we will have:

( 4.9)

where:

( 4.10)

and is the skew-symmetric matrix corresponding to the vector from Equation (4.6). The transformation (4.5) can be written:

(4.11)

or:

. (4.12)

Using the relation, (4.12) becomes:

( 4.13)

where is given by the relation (4.10).

If in the Equation (4.10) and the Equation (4.12) becomes:

( 4.14)

Theorem 4.1.

If has fixed direction, then the transform (4.5) has the following properties:

1) is -linear;

2);

3);

4);

5);

6)

7) is invertible and.

Proof:

1) -linearity of the correspondence (4.5) is a trivial consequence of a definition.

2) is a tensor function, given for any by a proper orthogonal tensor. The vector is a proper vector of this transformation for any, his direction, fixed, is the instantaneous axis of rotation:

. ( 4.15)

Equation (4.15) can be obtained directly from Equation (4.14).

The proper tensor preserves, for any, the cross products, because it preserves also the metrics and the orientation:

. ( 4.16)

From (4.16) using (4.15) it follows:

. ( 4.17)

The matrix form of the tensor relation (4.17) is:

( 4.18)

From Equation (4.18) it follows that the matrix and are commutative for any:

. ( 4.19)

3) We will prove the matrix form of Equation (3). Let be a solution of Equation (4.1), where is a matrix function corresponding to the proper orthogonal tensor, and is the column matrix associated with the vector function. The derivation of with respect to time is:

. ( 4.20)

Using Equation (4.1), Equation (4.20) will be written:

. ( 4.21)

Using Equation (4.18) we will have:

. ( 4.22)

The corresponding tensor of Equation (4.22) is:

. ( 4.23)

4) We will apply twice Equation (4.23):

( 4.24)

5) The transformed (4.5) being a proper rotation is also an isometry, so:

( 4.25)

6) In matrix notation we have. For we will have:

. ( 4.26)

Equation (4.26) can be also written:

. ( 4.27)

To compute using 3˚ and after Equation (4.27):

. ( 4.28)

7) Being an orthogonal transformation, is invertible. If the transformation tensor is, the transformation tensor is. To demonstrate that we will show that verifies Equation (2.1) with instead of.

From (4.1), by transposition, it follows:

. ( 4.29)

Knowing that is skew-symmetric, we have. Equation (4.29) will be written:

. ( 4.30)

From Equation (4.19), by transposition and considering, it follows:

. ( 4.31)

From Equations (4.30) and (4.31) we have:

. ( 4.32)

Therefore, so.

Note: The transformation, given by Equation (4.5), is a symbolic representation of a vector space in itself. The third property of Theorem 3.1 shows that we can define like unary operation on the relative derivation with respect to angular velocity, and like operator for symbolic representation the trivial derivation of vector functions of real variable with respect to the variable.

This transformation “gives an algebraic form” to a class of vector differential equations that model the motion of mechanical systems in non-inertial frames, whom are in the motion of non-uniform rotation, on fixed direction, also the motion with respect to the inertial frames in the fields of gyroscopic forces.

5. The Solution of the Reduced Form Problem

The motion of the Foucault Pendulum is described by the following non-linear initial value problem:

( 5.1)

If the force field is elastic, the type, , we will have the mathematic model of Foucault pen- dulum on a non-inertial frame that is rotating non-uniform on fixed direction:

( 5.2)

We will use the present method in order to resolve the reduced form of the problem (5.2):

( 5.3)

The mathematical model of the Foucault pendulum is presented of the type (5.3) in the theoretical mechanics [10] [11] . The problem (5.3) can be found from (5.2) neglecting the term, which represents the contribution of centrifugal force of inertia in the hypothesis. We will see that, paradoxically, the exact solution of the short form (5.3) is more difficult to obtain than for the complete problem (5.2).

1) If and, we are looking for the solution of the problem (5.3) with the property,. A such solution, if it exists, verifies the differential of the equation:

( 5.4)

The solution of the problem (5.4):

( 5.5)

verifies the initial conditions of (5.3) and has the property:,.

2) If and, we are searching the solution of the problem (5.3) with the property. Let be:

( 5.6)

Assuming from (5.6) it follows that. Now we will have:

( 5.7)

Therefore:

( 5.8)

Applying the transformation on the Cauchy problem (5.3), considering (5.8), we will have the problem:

( 5.9)

The solutions of (5.9) with the property is searched. In this hypothesis, the problem (5.9) becomes:

( 5.10)

The solution of the problem (5.10) is:

( 5.11)

In the hypothesis and, it follows, therefore, (5.11) is also the solution for the problem (5.9). On the same hypothesis the solution of the problem (5.3) is:

( 5.12)

Considering the fact that, the solution (5.12) will be written:

( 5.13)

Now, let be the Cauchy problems:

( 5.14)

( 5.15)

In accordance with those shown in the points a) and b) the solutions of the problems (5.14) and (5.15) are:

( 5.16)

where:

( 5.17)

respectively:

( 5.18)

where:

( 5.19)

with given by Equation (5.11). From (5.19) and (5.20), after elementary calculus, it follows:

( 5.20)

The relations, and of the linearity of the differential Equation (5.3) have the consequence that the solution of the Cauchy problem (5.3) is given by with and given by the relations (5.16) and (5.20). Finally, the results can be summarized as following:

Theorem 5.1:

The solution of Cauchy problem:

( 5.21)

is given by the vector function:

( 5.22)

where

( 5.23)

( 5.24)

Note: Also, the problem (5.21) shapes the movement of the vibration for a class of gyroscopic instruments. Even in the case of planar motion, the literature shows only the approximate solutions assuming with particular initial conditions as in the case of harmonic oscillator in magnetic field. The presented solution (5.22) is accurate.

6. Conclusion

The work presents the closed form vector solution for the well-known Foucault pendulum problem. Both forms of the Foucault problems (the whole form and the as known “reduced form” when the centripetal force is neglected) are considered. The last one models the movement of the harmonic oscillator in uniform magnetic field, also. Therefore, a specific isomorphism between the free vectors map and the column matrix map is used. The short solution of the Foucault pendulum problem is obtained using vectors as column matrix of complex numbers adequate defined. With this method, the second order Cauchy vector problem which describes the spatial movement of the Foucault pendulum becomes a first order differential matrix equation with constant coefficients. The closed form vector solution obtained in this way allows a suggestive kinematic representation of the spatial movement of the Foucault pendulum. The closed form vector solution for Foucault pendulum problem is obtained by means of a time dependent tensor operator which reduces this problem to only two classic problems very easy to be solved. The tensor operator as introduced can extend the study of all Foucault type movements in the case of non-inertial reference frame with time dependent angular velocity.

References