Received 4 January 2015; accepted 24 January 2015; published 27 January 2015

ABSTRACT

This paper establishes asymptotic time dependences of characteristic sizes of astrophysical and cosmological objects. These dependences are obtained on the basis of uncertainty principle applied in cosmic scales in approximation of spherical symmetry in Euclidean geometry. The proposed analytical approach makes it possible to determine spatial boundaries of the uniformity of matter distribution in the Universe, and a size of cosmic sphere which contains numerous groups of interacting universes.

Keywords:

Uncertainty Principle, Cosmos, Astrophysical/Cosmological Objects, Characteristic Sizes, Time

1. Introduction

At present the increasing number of scientific articles is devoted to different problems of astrophysics and cosmology: from formation and evolution of stars and galaxies to formation of the large-scale structure of the Universe under influences of dark matter and dark energy (see, for example, [1] -[10] ). The results of these investigations are based on reliable astronomic observations as well as on modern theoretical conceptions about formation and expansion of the Universe after Big bang. Theoretical investigations are connected with the ideas on behavior of gravitational fields and gravitating masses at diversiform possible geometries of cosmic space, in particular, at Euclidean, parabolic and hyperbolic geometries. A stochastic quantum nature of cosmological phenomena is noted.

The most significant cosmological problem is determination of spatial boundaries corresponded to uniformity and isotropy of the Universe, i.e., to Cosmological principle [1] -[3] . The latter signifies that because of insufficient time for growth of gravitational perturbations, the distribution of matter at early stages of formation of cosmological structures does not affect the average value of matter density in up-to-date cosmos, and “heavy heterogeneities and voids are ended at some very large but still unknown distance” [2] . Another significant problem is the following: is cosmos infinite or finite (closed) and where is a boundary of closed cosmic space [1] [2] ?

In accordance with conception [3] about a large-scale structure of the Universe as of non-uniform matter distribution originating from growing adiabatic perturbations of density, there is some distinction between the developed non-linear structures within the scales of less than 10 Megaparsec (Mps) (namely, halo of the galaxy, groups and clusters), and the structures with more regular quasi-linear matter distribution within the scales of up to 100 Mps, i.e. superclusters and cosmological “voids”. It should be noted that up-to-date the quasi-undisturbed Hubble flow of matter that has been already affected by quantum-gravitational instabilities, still continues.

In this paper, an attempt of qualitative analysis of the above problems is undertaken. With this purpose, extended interpretation of an uncertainty principle applied to the sizes of objects in cosmic scales is proposed. The proposed analytical approach makes it possible to obtain asymptotic time dependences for characteristic sizes of astrophysical and cosmological objects in approximation of spherical symmetry in Euclidean geometry. Globular star clusters, superclusters of galaxies and the Universe itself are considered as such objects. The existence of groups of interacting universes is postulated, and the issue of a size of cosmic sphere involving the great number of such groups is considered.

2. Phenomenological Approach

By analogy with quantum mechanics which considers discrete and continuous energy spectra of microcosm objects it is possible to single out relatively small-scaled regions for cosmic structures, where, as a result of gravitation, mass distribution is non-uniform (analogy is with discrete energy spectrum). In more extended structures, where gravitation “gets smeared” (spreads) in space, mass distribution becomes quasi-uniform (analogy is with continuous energy spectrum).

Such analogy provides precondition for an attempt to extend the uncertainty principle to cosmic scales. The essence of the proposed uncertainty principle in cosmic scales is in the fact that during the time of a single act of gravitational interaction between cosmic structures, their sizes cannot be determined exactly. It is connected with the fact that unless the elementary act is finished, it is impossible to determine to which object each of the interacting surface elements the most closely located to each other is assigned. Stars are elements for globular clusters, galaxies are elements for super-clusters, clusters of galaxies are elements for the Universe.

In accordance with the generally accepted concept about formation of large cosmological objects from smaller ones (embryos) [2] , we will consider closed systems whose sizes increase due to interaction of many embryos between themselves and interaction of objects between themselves. A process of irreversible aggregation of objects is described using a concept of distribution density wave φ(a, t) in the space of cluster sizes a. The wave propagates with the time t toward an increase in the cluster size. Such one-dimensional approach allows one not to take into account deviation of a geometrical shape of the object from the ideal spherical one.

On the basis of universal relation for half-width of wave packet and half-width of spectral line (resulted from Fourier theorem) 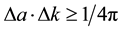(k is wave number), it is possible to write down the following uncertainties relation for a coordinate and a momentum in space of sizes a:

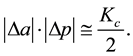(1)

Here 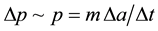is uncertainty of momentum, 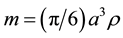is object mass with the density ρ; K_c is 2π-reduced cosmological constant of action; 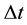is a typical time period for a single act of object interaction. Uncertainty of momentum by an order of magnitude is equal to momentum itself, since gravitational interaction between objects occurs always. Cosmological constant of action can be determined (by analogy with the Planck mass and length) from consideration of dimensionality as:

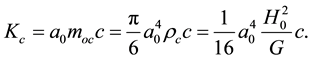(2)

Here 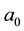is a typical size of embryos from which an object is formed; c is velocity of light in vacuum, 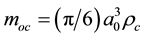is conditional mass of an embryo with the critical substance density 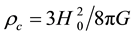[4] , above which the Universe becomes closed; H₀ is Hubble constant, G is gravitation constant. Hence it follows that each type of the objects under consideration has own cosmological constant of action: the larger a structure embryo is, the larger K_c is.

Formally, it follows from ratio (1) that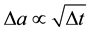, i.e. the instantaneous rate of growth of object size is infinite:

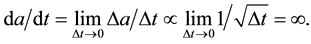
That means that formation of a large-scale Universe structure is of pulsed nature, i.e. there is development of initial perturbations in matter distribution as a result of instability of cosmological flows leading to appearance of non-uniformities. If perturbations are not large, it is reasonably to consider the mean size 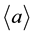of objects.

In case of intensive process of object interaction (at close distances or at large flows of dark mass-energy) the value 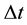can be determined from the “energy-time” uncertainty relation:

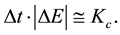(3)

Here ∆E is energy level width, corresponding to a specific process. Since in relations (1) and (3) we are dealing with object sizes that vary continuously with time, these relations can be considered as differential. From the relations (1) and (3) we obtain the following differential relation:

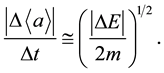(4)

From here it is obvious that in intensive processes the action constant becomes “virtual”.

3. Calculations of Characteristic Sizes of Astrophysical and Cosmological Objects

We consider globular clusters consisting of red giants having an average mass of m_g = 4M_S, where M_S is the mass of the Sun [11] . In Newtonian approximation, the gravitational energy (work) necessary for separation of a giant from the surface of a globular cluster or for its capturing from space by this cluster surface, is equal in absolute value to

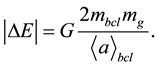(5)

Here m_bcl is the mass of globular cluster, is its characteristic diameter. Substituting Equation (5) into Equation (4) and solving it in quadratures with regard to zero initial condition, we obtain the following relation between the characteristic diameter of globular cluster and the time:

(6)

With the Universe life time [1] -[3] , the calculated characteristic diameter of globular clusters is equal to (630 light years). The diameter of the well observed globular cluster Omega Centauri is equal to 600 light years [12] .

Thus, the uncertainty principle works well enough within the range of astrophysical scales. This suggests that it might be used in cosmological scales. As we accept a characteristic time of perturbation travel over a cosmological object:. One can expect that during this time interval the matter density in the object remains invariable. Substituting Equation (2) into relation (1) rewritten for the mean size, we obtain the following differential relation:

(7)

Here clusters are embryos for superclusters, and superclusters are embryos for the Universe.

Solving Equation (7) in quadratures with regard to the initial condition, we obtain the following asymptotic dependence of the mean size of the object on time:

(8)

This dependence is valid up to the “moment” of time t₁, from which dark energy begins to prevail in matter density in the Universe. In accordance with generally accepted ideas [3] , dark energy prevails in matter density for 3.5 billion of years, which is significantly less than the Universe life time.

Let us calculate consecutively theoretical sizes of the considered structures according with Equation (8) based on the data [1] : ρ_c/ρ = 33,. In accordance with ideas [2] [3] , it is reasonably to accept galactic clusters as “the least element” of large-scaled structure of the Universe. A reliably observed mean size of galactic clusters is approximately equal to [11] . Having accepted this value as, we find out that with the time, the calculated mean size of superclusters is approximately equal to. It should be noted that the observable sizes of superclusters are in the range 30 - 100 Mps [3] [11] . And void sizes are approximately equal to sizes of superclusters [3] . The value can be assumed to be “low” in size ranging. From this point on, matter mass distribution in the Universe becomes quasi-uniform. Having taken this value as the size a₀ of embryo of a larger isotropic structure we find out that the calculated characteristic size of the Universe at the time t₁ is equal approximately to. One can assume that upper boundary of the Universe is equal to

.

It should be noted that the size R_un is significantly less than the “light” radius. This circumstance signifies the possibility for interactions within a group of universes, located in the region with the size R_light. By analogy with microcosm and mesocosm the exponent 1/3 attached to t in Equation (8) corresponds to Brownian motion of colliding objects, and the final result of collisions consists in irreversible aggregation of objects [13] . In terms of this paper the result of “collisions” between cosmological objects is in their interpenetrations occurring in near-surface regions and in appearance of dark matter and dark energy in these regions. This results in significant increase of expansion rate of the Universe. Substituting into Equation (4), we obtain that starting with t₁ the time dependence of characteristic size of the Universe takes the following form:

(9)

The second term in Equation (9) expresses the ultimate ultrarelativistic stage of Universe expansion with the constant velocity. Hence it follows that the upper evaluation of characteristic size of the Universe “at present” is equal to. This value is less than the up-to-date light radius which is equal to. This will produce an opportunity for interactions within the group of “closely spaced” universes, whose possible number is evaluated as.

4. Cosmic Sphere

Let us consider an issue about a size of closed cosmic sphere which contains a great number of groups of interacting universes. We will determine the ultimate value of cosmological action constant on the basis of analogy with the Planck mass, which is determined using action constant in microcosm, gravitation constant G, and velocity of light c. For one can write down the following equation:

(10)

Here, is cosmic mass determined as product of baryon mass and the ratio of critical density to baryon density; m_p is proton mass; N_b ~ 10⁸⁰ is number of baryons in the Universe [1] . The value M_c corresponds approximately to the cosmic mass 3.986 × 10⁵⁴ kg, given in [14] . Reference [14] is devoted to values of physical constants. Substituting expression (10) into Equation (1) and fulfilling the procedure described above, and assuming that the least time period of a single act of interaction between the objects under consideration is equal to time of perturbation travel over galactic cluster (homogeneous structure element), we obtain the following asymptotic equation for cosmic sphere at present “moment” of time:

(11)

The exponent 2/5 attached to t corresponds to the analogy with free-molecular flux of Brownian particles, i.e., with irreversible growth of object as a result of successive addition of structure elements. With ρ = 0.03ρ_c [1] , [3] , we obtain that with the observed cluster size [11] and with the above stated life time of the Universe, the unknown quantity is equal to, i.e., a radius of closed cosmic sphere is equal to. This value exceeds the “light” radius R_light by almost two orders of magnitude. Hence one can conclude that all interactions within the cosmic sphere can occur only between “neighboring” universes with sizes and distances between them which not exceed the distance travelled by light. The interacting universes are formed independently from each other, for example, as a result of great number of “Big bangs” distributed in space and time randomly inside the sphere (11). Number of universes formed inde-

pendently inside the cosmic sphere can be evaluated as. And the number of independent groups of interacting universes can be evaluated as. These values extend the notions [8] on large numbers in quantized cosmos.

5. Discussion of Results

A distinctive feature of this phenomenological approach is in assumption of the existence of many interacting universes in space with spherical Euclidian geometry and in introduction of the concept of cosmological action constant, the value of which depends on a scale of a cosmological object, which is an embryo for a larger structure under consideration. The given results do not contradict to well known ideas [1] -[3] about the sizes of astrophysical and cosmological objects. In addition, the second term in Equation (9) qualitatively reflects the presence of cosmological “repulsion” of objects (antigravitation) at a limiting ultrarelativistic stage of the Universe expansion at a constant velocity. This corresponds to the consensus about nonzero positive cosmological constant Λ > 0, mentioned in R. Penrose monograph [1] .

To describe an intermediate stage of expansion affected by dark energy one can accept the value of mass in Equation (10) for cosmological constant of action as equal to the ultimately possible value. Substituting this equation to relation (1) rewritten for the mean size, and fulfilling the procedure described in section 3 with, we obtain the following differential relation:

(12)

Here. Having solved Equation (12) in quadratures with the initial condition

(see Equation (9)), we obtain the following equation for the Universe size-time relation:

(13)

This equation reflects accelerated expansion, and the type of time dependence of characteristic size of the Universe is in compliance with de Sitter cosmological model for Euclidean geometry at Λ > 0. The type of pre-exponential factor corresponds to Dirac cosmological model for Euclidean geometry at the atomic time scale when Λ = 0 [15] . In addition, relation (12) with the consideration for the above given ρ_c and ρ is rearranged to the following equation:

(14)

Equation (14) corresponds approximately to the Hubble law.

Thus, uncertainty principle and Cosmological principle do not contradict each other and are mutually complementary. The presented results correspond to fundamental concept [10] of stochastic quantum nature of cosmological phenomena.

From Equation (13) we obtain that the universe size at present stage is. Hence we get that the maximum number of universes inside the cosmic sphere is, and the maximum number of interacting universes in the region with the size equal to the light radius is equal to. The existence of the great number of mutually interacting universes does not contradict to the statement about existence of a set of images of “unique sample” described by R. O. Bartini in [14] .

The above results are obtained in one-dimensional approximation. With more complicated space-time geometry proposed in [14] the value of cosmic radius is. The discrepancy of the above value and R_cB is not essential, since both values are much larger than the light radius. If one substitutes theoretical formation time of large-scale structure of the Universe (which is equal to 2.2×10¹⁰ years [3] ) into Equation (11), then the value of the cosmic sphere radius will be. The discrepancy with R_cB becomes insignificant.

It should be noted that the proposed approach does not assume any prohibitions on existence of great number of independent cosmic spheres (11) in infinite space.

6. Conclusion

Extended interpretation of uncertainty principle applied to the sizes of objects in cosmic scales in approximation of spherical symmetry in Euclidean geometry was proposed. Evidently first phenomenological outer-space constant of action was determined with regard to the sizes and masses of embryos of astrophysical and cosmological objects. The obtained adequate asymptotic time dependences of characteristic sizes of objects under consideration demonstrate that the “ordinary” space-time relations are valid for determination of cosmic boundaries. The presented results indicate the existence of the great number of independent groups of interacting universes. The proposed approach does not contradict to well-known ideas about stochastic quantum nature of cosmological phenomena and completes the existent notions on large numbers in quantized cosmos.

References