World Journal of Mechanics
Vol.04 No.10(2014), Article ID:50450,5 pages
10.4236/wjm.2014.410030
Generalized Orbitals under the Influence of 2D Central and Noncentral Forces
Haiduke Sarafian
The Pennsylvania State University, University College, York, USA
Email: has2@psu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 July 2014; revised 18 August 2014; accepted 15 September 2014
ABSTRACT
In polar coordinate system, we consider fifteen classes of forces resulting in unlimited undiscovered orbitals. The classic conic orbits are one of the special subclasses of the fifteen classes. Among the rest of the forces, we show a few instances displaying typical fresh orbitals. Aside from the common theoretical foundation, the specifics of the orbitals are given by the solution of corresponding equations of motion. These are coupled nonlinear differential equations. Solving these equations numerically, utilizing a Computer Algebra System such as Mathematica is conducive to the orbits. Simulation of the orbitals provides a visual understanding about the motion under the influence of the generalized noncentral forces.
Keywords:
Generalized Orbitals, Noncentral Forces, Mathematica

1. Introduction
In our previous work, we investigated the motion of a massive point-like particle under the influence of semi generalized central forces [1] [2] . In a polar coordinate system, we consider that forces are merely radial and distance dependent. The scope of the investigation is 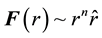 where n is within
where n is within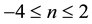 . This specific range includes two particular instances, namely n = ‒2 and 1. The former specifies the gravity and electrostatic forces i.e. the Keplerian forces, and the latter is merely a linear force. Consequently, the former gives the classic conic orbitals and the latter induces the Elliptic Harmonic orbits. The rest of the suggested n values give peculiar orbits discussed in [2] . In our approach, we outline the general theoretical foundation; as such one has the option of selecting unrestricted values for n including reals. Motivated with the outcome of our study, we craft our current analysis. This augments our previous work in three major frontiers. First, we consider radial forces that are not merely distance dependent. Forces such as,
. This specific range includes two particular instances, namely n = ‒2 and 1. The former specifies the gravity and electrostatic forces i.e. the Keplerian forces, and the latter is merely a linear force. Consequently, the former gives the classic conic orbitals and the latter induces the Elliptic Harmonic orbits. The rest of the suggested n values give peculiar orbits discussed in [2] . In our approach, we outline the general theoretical foundation; as such one has the option of selecting unrestricted values for n including reals. Motivated with the outcome of our study, we craft our current analysis. This augments our previous work in three major frontiers. First, we consider radial forces that are not merely distance dependent. Forces such as,  and
and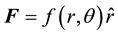 , here
, here 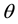 is the polar angle. The f’s are arbitrary functions; consequently there are unlimited corresponding orbitals. Secondly, in a polar coordinate system, we consider forces that are merely azimuthal such as,
is the polar angle. The f’s are arbitrary functions; consequently there are unlimited corresponding orbitals. Secondly, in a polar coordinate system, we consider forces that are merely azimuthal such as, 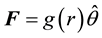 ,
, 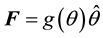 and
and  . Similar to the previous case g’s are arbitrary functions, therefore there are unlimited orbitals. Thirdly, we envision two-component forces, i.e. forces with radial and azimuthal components. A complete set of such forces are tabulated in Table 1. The table includes fifteen classes. These are called classes because each one embodies countless forces; these are labeled fij and gij. The main objective of our investigation is to apply the classical mechanics analyzing the orbitals of a massive point-like particle undergoing the influence of tabulated forces in Table 1. This work is composed of four sections. In addition to Motivation and Goals, in Section 2 we outline the general foundation of our analysis. In Section 3 for a few random cases, we simulate the orbitals. We close the work with concluding remarks.
. Similar to the previous case g’s are arbitrary functions, therefore there are unlimited orbitals. Thirdly, we envision two-component forces, i.e. forces with radial and azimuthal components. A complete set of such forces are tabulated in Table 1. The table includes fifteen classes. These are called classes because each one embodies countless forces; these are labeled fij and gij. The main objective of our investigation is to apply the classical mechanics analyzing the orbitals of a massive point-like particle undergoing the influence of tabulated forces in Table 1. This work is composed of four sections. In addition to Motivation and Goals, in Section 2 we outline the general foundation of our analysis. In Section 3 for a few random cases, we simulate the orbitals. We close the work with concluding remarks.
2. Analysis of the Physics Problem
Following the objectives outlined in the previous section we consider the kinematics of a mobile massive point- like object of mass m in a two-dimensional space. Utilizing the polar coordinate system the acceleration is [3] [4] ,
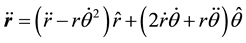 (1)
(1)
where according to the standard convention a single-dot and a double-dot are the first and the second derivatives with respect to time, respectively. Applying (1) the equation of motion is,
 (2)
(2)
The RHS of (2) is one of the fifteen cells of Table 1. Accordingly, (2) is a representative equation of motion. For instance in our previous work [1] [2] we consider the impact of the content of cell12; namely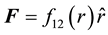 . More specifically, we consider
. More specifically, we consider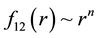 . For this class of forces the absence of the azimuthal component of the force assists decoupling the associated equations results a single differential equation. Solution of the latter gives the desired orbitals. In general applying the latter procedure yields (2),
. For this class of forces the absence of the azimuthal component of the force assists decoupling the associated equations results a single differential equation. Solution of the latter gives the desired orbitals. In general applying the latter procedure yields (2),
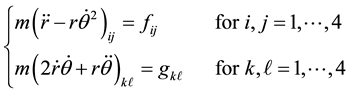 (3)
(3)
The set of equations given in (3) are coupled ODEs. For arbitrary functions such as 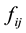 and
and 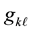 most likely (3) is nonlinear. Unless otherwise for appealing cases one doesn’t seek for their analytic solutions. Utilizing Mathematica [5] we solve (3) numerically.
most likely (3) is nonlinear. Unless otherwise for appealing cases one doesn’t seek for their analytic solutions. Utilizing Mathematica [5] we solve (3) numerically.
3. Results
In this section according to Table 1 for a hand full of cases we investigate the specifics of the motion. Generally speaking, (3) is a set of coupled differential equations, aside from the force constant (see next paragraph) their numeric solutions require a set of four initial conditions. As one expects, the solutions are sensitive to the force strength and the initial conditions. Solutions are expressed as . Utilizing these we identify the orbitals and quantities of interest. We give examples highlighting the specifics.
. Utilizing these we identify the orbitals and quantities of interest. We give examples highlighting the specifics.
Example 1. Consider the well-known gravity and electrostatic force i.e. the Keplerian forces. The force falls
Table 1. Symbolic representation of fifteen possible classes of forces with components along the radial and azimuthal directions in a polar coordinate system.
in the category of cell12 of Table 1. We substitute 


stance, in the case of gravity the value of 
constant and M is the central mass. In the case of charge-charge interaction 

tric coupling constant and Q, q are the charges of the point-like charges. By trial and error the initial conditions and the force constant are adjusted so that the orbital is a perfect stable circle. One such set of parameters is given in the figure caption of Figure 1(a). It is reassuring that the output of our current approach is the same as [2] . It is noteworthy mentioning that one of the objectives of our current investigation is to numerically solve more challenging issues, see examples 2, 3 and 4; where in [2] compatible with its objectives the emphasis was on less generalized case studies.
Figure 1(a) is comprised of three panels. The left plot displays the Cartesian components of the particle position. These are
By adjusting the initial radial velocity the stable circular orbit of Figure 1(a) becomes a perfect, stable elliptical orbit. Figure caption of Figure 1(b) includes the specifics of the force strength and the initial conditions.


Figure 1. (a) The orbital is a perfect stable circle. The force strength is x = 4.5, and the initial values are 

The left plot of Figure 1(b) seemingly is similar to the corresponding Figure 1(a). However, there are minor, hard to see differences. These are shown in the middle plot of Figure 1(b). Its mildly wobbling behavior warrants non-circular, elliptic orbit shown in the right panel of Figure 1(b).
In this case too our current output coincides with our previous work [2] .
Example 2. Here we consider an example associated with the cell13. We equate




For a set of parameters specified in the figure caption of Figure 2 we display graphic information including the orbital.
Description of the individual panel is the same as in the previous examples. It is worthwhile noting unlike the previous examples the orbital is not stable. The character of the pure radial force makes the particle orbiting about the center and then wandering away, tracing a non-returnable trajectory. For a better descriptive word maybe in this case “orbital” should be called “trajectory.”
Example 3. Here we consider an example associated with the cell14. We equate
is the force constant. The spirit of this theoretical suggested force is similar to the previous example. Meaning, no such force has been observed in nature, yet! However, as mentioned before, the analysis paves the road for the “what-if scenarios.” Similar to the previous examples the angular momentum of the particle is conserved. For a set of parameters specified in the figure caption of Figure 3 the graphic information includes the orbital.
According to the plot of the middle panel the radial distance of the particle is a diminishing oscillatory function with respect to time, t. Its polar plot shown in the right panel is an interesting unstable orbital. Here the particle interestingly orbits about the center and contrary to example 2 stays in sight.
Example 4. As a last example we consider a case associated with cell32. We equate 

individual force strength x along the radial and the azimuthal directions. This example, unlike the previous ex-
Figure 2. The force strength is x = 2.25, and initial values are
Figure 3. The force strength is x = 4.5,and initial values are
Figure 4. The common force strength is x = 5.15 and initial values are
amples, doesn’t conserve the angular momentum. For a set of parameters specified in the figure caption of Figure 4 the graphic information includes the orbital.
The orbital shown in the right panel is somewhat interesting. The rest of the plots are self-explanatory.
4. Conclusions
Motion of a particle under the influence of conventional forces such as gravity and electrostatic is known [3] [4] [6] [7] . These forces are purely radial and do conserve the angular momentum. The corresponding equations of motion are solvable analytic differential equations. The orbitals are stable conic sections. Advances in CAS make it possible to augment the area of the study. As such, our current work investigates the impact of generalized forces on the orbitals. Our work even augments our previous work [1] [2] . We have introduced fifteen classes of forces. We show the details of only a handful of cases. However, according to what we have introduced in the text, our approach recognizes no limitation. As we mentioned in the Motivation and Goals section and in the body of the text of example 2, the freedom of choosing the force functions in any of the fifteen classes puts no limit on our theoretical investigation. To the author’s knowledge, there are no other comparably investigated reports in this area.
Our approach is purely numeric and is based on numeric solution of differential equations provided by Mathematica. We include a Mathematica code so that the interested reader is able to apply the code investigating the orbitals/trajectories of a particular force.
Acknowledgements
The author appreciates the referee’s comments.
References
- Sarafian, H. (2014) Central Conservative Forces and Orbits beyond Conic Sections, Progress on Difference Equations. Abstract Book, 58, Izmir University of Economics, Turkey.
- Sarafian, H., Takato, S., and Kaneko, M. (2014) Central Conservative Forces and Orbits beyond Conic Sections. The Journal of Mathematics and System Sciences, 4, 579-585. www.davidpublishing.org/journals_info.asp?jId=2039
- Thronton, S. and Marion, J. (2003) Classical Dynamics of Particles and Systems. 5th Edition, Cengage Learning, Boston.
- Symon, K.R. (1965) Mechanics. 2nd Edition, Addison-Wesley, New York.
- Wolfram, S., (2012) Mathematica: A Computational Software Program Based on Symbolic Mathematics, V9.0.
- Goldstein, H., Safko, J. and Poole, C. (2001) Classical Mechanics. 3rd Edition, Addison-Wesley, New York.
- Arya, A.P. (1990) Introduction to Classical Mechanics. Allyn and Bacon, London.
Appendix
Mathematica code. Here is the code that runs Example 4 in the text. In this example the right hand sides of (3) are −xr(t) and −xq(t), respectively. However, the given code can run for any desired case. To do so in the first line of the code one needs to replace the right hand side of the corresponding equations with the appropriate functions.






