Received 19 June 2014; revised 15 July 2014; accepted 9 August 2014

ABSTRACT

This work is concerned with the estimation from the outside of effective yield strength for the stage II consolidated material package of axisymmetric solid particles. Once an appropriate simple representative axisymmetric unit cell is chosen, the kinematical approach of the yield design homogenization method is used in order to obtain external estimates which has been found depending on the loading history (isostatic and closed die compactions) as well as on the relative density of the material powder. For comparison purpose, finite element simulations that describe the behavior of spherical elastic plastic particles uniformly distributed inside the material powder are carried out.

Keywords:

Stage II Compaction, Kinematic Approach, Relevant Failure Mechanism, Unit Cell Model, Effective Yield Strength, Finite Element Analysis

1. Introduction

Isostatic and closed-die compaction are useful methods to manufacture complex shape engineering components such as, for example, gears, and cams for automotive applications. The ability to control accurately the size, composition and morphology of the microstructure, as well as the ease of processing are major advantages of the process. Consolidation in powder compaction occurs simply by the motion of particle centers toward each others by mechanisms of rearrangement and deformation. Nowadays the process of compaction is a successful and well-established process for metals, alloys, polymers and ceramics. It is usually divided into two stages according to packing state change and relative density. For the first stage, referred to as “stage I”, relative density is low 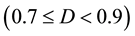and consolidation of the powder is attributed to both changes in particles packing and particle deformation by growth of localized necks between particles. In the second stage, referred to as “stage II”, at higher compacted relative densities, consolidation occurs purely by plastic deformation. The change in component dimension is much greater during stage I than in stage II compaction. It should be mentioned that a stage II powder is different from a porous solid (or sintered powder) of equal relative density in that the former has zero or low cohesive strength, while the later usually has tensile strength equal to the compressive one. Densification of the compact is achieved at elevated temperature with or without the simultaneous application of pressure [1] [2] . The present paper is concerned with the theoretical estimation “from the outside” of macroscopic yield surfaces for cold pressed powder in stage II at fixed relative density.

In modeling the compaction process, the powder medium is considered as a solid with isolated voids that undergoes large elastic-plastic deformation. Numerous theoretical, numerical and also experimental studies have been published on the subject. A review as well as further details dealing with powder compaction modeling can be found for example in [3] [4] . The used phenomenological models provide information on the macroscopic behavior of the powder assembly such as density distribution, stress state and the shape of the compact during and after compaction. For describing the plastic flow of metal powders at low homologous temperature, Gu et al. [5] have developed a “two-mechanism” rate-independent constitutive model representable as a combination of a distortion mechanism and a consolidation mechanism which are dominated at the microstructural level by inter-particles sliding and the deformation of particles, respectively. Research work based on micromechanical approach has been initiated and developed by Ashby and co-workers (see for example the reference mentioned above) and Fleck et al. [6] [7] . Basically, the essential physics are the relationship between the macroscopic strain and the micro-mechanics of grain contact deformation, and the relationship between local contact loads and the resulting macroscopic stress. Fleck et al. [6] used the Bishop and Hill [8] method to estimate the macroscopic yield surface for a random aggregate made from rigid-perfectly plastic spheres. The roles of inter-particles friction, cohesive strength of the contacts and anisotropy resulting from grain periodicity upon the macroscopic yield surface was examined by these authors and also by Xin et al. [9] . The later used explicit Finite Element Analysis (FEA) to simulate monolithic and composite powders consisting of periodic unit cells. They concluded that the size and the shape of the macroscopic yield surface is sensitive to the magnitude of the cohesive strength between particles but the effect of friction is relatively minor.

In this study, in the framework of the kinematic approach of the Yield Design Homogenization Method (YDHM) [10] - [13] , external estimates of the effective yield strength of an array of axisymmetric particles are determined for both modes of compaction. In this context, since the yield design theory stipulates that large geometry changes are precluded, an appropriate axisymmetric Representative Volume Element (RVE) for material powder in stage II at fixed relative density is proposed together with four axisymmetric relevant (virtual) velocity fields. Similar investigations have been carried in [14] for stage stage II compaction using another appropriate axisymmetric RVE. For comparison purpose, Finite Element (FE) simulations similar to those of Ogbanna and Fleck [15] for spherical elastic plastic particles uniformly distributed inside the consolidated material powder are carried out. They have been used to examine the evolution of contact size, contact pressure and macroscopic yield surface with the degree of consolidation.

2. Representative Volume Element

The first step in micromechanical constitutive modeling is the suggestion of a RVE which adequately captures essential features of the underlying microstructural geometry and deformation modes of the heterogeneous material under consideration. On the other hand, a convenient way to numerically solve the homogenization problem is to use periodic boundary conditions applied on a periodic unit cell. The two other commonly used boundary conditions are the homogeneous boundary strain rate condition and the homogeneous boundary stress condition. Both homogeneous and periodic boundary conditions may introduce additional constraints resulting in “biased” numerical solutions including boundary effects and eventually unrealistic stiff response (See in [16] the discussion about the minimal boundary conditions applicable to a RVE of any shape). Periodic boundary conditions require periodic spatial distribution of the microstructure, and this enables the approximation of the heterogeneous material by an indefinite extension of a periodic elementary cell in the three dimensions of space. This assumption has been widely used in the literature as it requires the modeling of only the highlighted elementary cell, greatly saving computational cost. The arrangement of particles for this study is shown in Figure 1(a). The powder compact is considered as an assemblage of hexagonal cylinder unit cells filled with an axisymmetric cylindrical particle (Figure 1(b)). The assumption of regularly (instead of random) packed mono-

sized particles substantially simplifies the analysis as the entire densification process can be analyzed from relatively simple unit cell calculations. However, it should be mentioned that the stacked hexagonal array RVE assumes a rather unrealistic particle distribution, and as a result, desired modes of deformation such as interparticle shear are restricted.

The plastic deformation of particles during stage II compaction is confined in the vicinity of small traction- free voids since the interaction of plastic contact zones is such that the solid material is forced to be extruded towards the traction-free voids. For the sake of simplicity and having regard to the smallness of the traction-free void with respect to the particle dimension, the boundary of the void is assumed diamond shaped with edge (Figure 1(b)). This claim is consistent with FE results presented in section 5 and dealing with the deformation mode of spherical particle for various initial relative densities. Let us consider an axisymmetric RVE Ω of a powder compact with a relative density corresponding to stage II compaction, that is.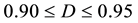

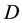
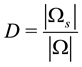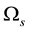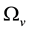is defined by the ratio, where and denote the parts of Ω occupied by the solid particle and

the void, respectively and 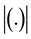stands for the volume of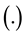. In the undeformed configuration, Ω is a circular cylinder with diameter 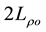and height 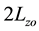filled with an circumscribed axisymmetric cylindrical particle with chamfered edges (initial length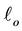). Along the compaction process the current values of diameter, height and chamfer length fulfill the constraint

(1)

The macroscopic response of the unit cell model is given by the average state of strain and stress within it. Its overall deformation can be calculated from the normal displacements of both rigid plates. Apparently, the macroscopic total logarithmic strains tensor and Cauchy stresses tensor possess the same principal directions, which are the radial and axial directions. The logarithmic radial and axial strains are given by

(2)

The effective strain defined by

(3)

is chosen as the overall plastic deformation of the unit cell model and the independent variable for presenting most results. We introduce and as the macroscopic isostatic and deviatoric stresses, respectively, and their expressions are

(4)

where and denote, respectively, the remote macroscopic radial and axial stress on the walls of the unit cell. Let us mention from now on that 1) for isostatic compaction the logarithmic strains and are equal:; 2) for closed die compaction (i.e. uniaxial straining):; 3) for uniaxial compression (with no radial constraint): and; and 4) for radial compression (with no axial constraint): and.

In the next two sections the unit cell model, representative of the powder compact during stages II compaction process, at given relative densities ranging between and, is used as RVE to derive external estimates of effective yield strength.

3. Basics of the Yield Design Homogenization Method

The average of a field over the domain occupied by is denoted by. For a given second order tensor, let be the set of microscopic (virtual) velocity fields characterized by

(5)

with, is periodic and. The symmetric part of is

(6)

where denotes the outer boundary of and is the outer unit normal vector to. Let be a

microscopic stress field in equilibrium with in the sense of the average rule. Hill-Mandel'lemma

states that:

(7)

with. The determination of the macroscopic strength of an arbitrary periodic

heterogeneous medium reduces to solving a yield design boundary value problem defined over a RVE [12] [13] . The static definition of reads

(8)

The convexity of forall implies the same property for the domain [13] . Constituent material of the solid grain is characterized by von Mises strength criterion with uniaxial yield stress:

(9)

where is the deviatoric part of. The support function which is defined on the set of symmetric

second order tensors and is convex with respect to, accordingly reads [10] [11] :

(10)

with. If the (virtual) velocity field is discontinuous across a velocity jump surface with unit

normal vector, the expression of the support function is given by

(11)

Velocity fields complying with constraints of zero volume change (i.e. or) are termed relevant. Let us keep in mind that for a specified, represents the maximum resisting power the material can afford.

The dual definition of may be expressed through its support function defined as

(12)

where denotes any symmetric second order tensor. The limit stress states at the macroscopic scale are of the form

(13)

Using Hill’s lemma (7) together with the definition Equation (12), de Buhan [13] has noticed that, for any periodic perturbation, the support-function may also be computed as

(14)

The domain may also be characterized as the convex envelope of tangent hyperplanes:

(15)

4. External Estimates of Effective Yield Strength

External estimates of effective yield surfaces of powder compacts at fixed densities are derived through the fundamental inequality of the yield design kinematic approach, using four classes of virtual velocity fields for appropriate unit cell model. For a broad and systematic treatment of the yield design kinematic theory, we refer the reader to one of the excellent reviews by Salençon [10] [11] . This approach is but the dualization of the static reasoning by means of the virtual work principal. Its implementation relies upon the fundamental inequality

(16)

where is the power performed by external loading in the virtual velocity field (so-called failure mechanism) and is the maximum resisting power developed by the material on account of its strength. The general expression of is given by

(17)

where is the domain occupied by the mechanical system under consideration and is a surface across which the velocity field is discontinuous. An important part of the solution procedure is the optimization of the virtual failure mechanisms in order to obtain the best external estimate for the ultimate loads supported by the structure under consideration. For each separate geometrical configuration of the considered classes of virtual mechanisms, an optimization problem is solved. It concerns the minimization of a nonlinear objective function depending on a finite number of bounded variables, namely the geometrical parameters used to define the shape of each geometrical configuration.

4.1. First Proposed Class of Virtual Velocity Fields

Using cylindrical reference coordinate system with radial coordinate, circumferential angle and axial coordinate, the unit cell is assumed to be subjected to axisymmetric deformations so that all field quantities are independent of. In order to comply with the incompressibility constraint (i.e.) a continuous virtual velocity field necessarily has the general expression

(18)

where and are constants to be determined. Figure 2 schematically shows the relevant class of virtual velocity field which analytical expression is given by

(19)

The three zones , ‚ and ƒ are separated by two velocity jump axisymmetric surfaces, the cross sections of which by the figure plane are the lines and to be determined. There is interaction between the plastic zones of the grain which are in contact with the surrounding grains. The virtual motion (19) is such that 1) the volume  is given a downwards axial uniform translation velocity; 2) a continuous velocity field is given to the volume ‚, while the remaining part of the unit cell is kept motionless:. The failure pattern depends upon one dimensionless geometrical parameters, with, which position the end point of the failure lines and. The constants, and allow to precise the shapes of these failure lines. Indeed, to fulfill the slip condition across the lines and, it can readily be shown that necessarily the polar equations of these lines are respectively

(20)

with for failure line and

(21)

with and for failure line. The components of the macroscopic stress tensor can be calculated using one of the following expressions

(22)

where is the traction on the boundary of the unit cell. Accounting for the particular situation at hand, it is an easy matter to establish the following expressions giving the radial and axial macroscopic stress components in terms of whether averages of radial and axial contact pressures, or the statically associated radial and axial loads:

(23)

The general form of the virtual power performed by external loading for any velocity field reads

(24)

where the dot stands for the inner product of vectors. For the velocity field, Equation (24) reduces to

(25)

The maximum resisting power developed by the unit cell at hand in the proposed failure mechanism

arises from the velocity jump along lines, and also within volume ‚ where the virtual

velocity is continuous. writes then

(26)

with

(27)

Comparing (26)-(27) and (25), the fundamental inequality (16) results in:

(28)

which may be rearranged to provide upper bound solutions to the normalized macroscopic axial stress once the normalized macroscopic radial stress is given a particular value. Indeed, one has

(29)

where

(30)

Whenever the geometric parameter which settles the virtual motion, takes all admissible values, the inequality (29) is associated to a family of necessary conditions for stability. The best upper bound is derived from this inequality when is chosen such that the function is at minimum. Thereupon the parameter associated with the minimum of defines the critical volume  and ‚ of the solid grain and the corresponding potential slip failure lines and. In other words, in order to optimize the proposed failure mechanism family, has to be minimized with respect to. The minimum value is reached for satisfying the equation

(31)

The relationships contained in Expressions (30) are too involved to allow differentiation to derive directly the critical condition, and the procedure is cumbersome. Alternatively, the optimization of the proposed virtual failure mechanism in order to obtain the minimum upper bound for the ultimate loads supported unit cell is performed through the numerical minimization of with respect to parameter under the constraint. In this study, the problem is solved using simple in-house Fortran code. This proves to be accurate, computationally very cheap, and results in the best upper bound, considering the class of velocity field, of, that is

(32)

In the macroscopic stress plane reported to macroscopic normalized stresses axes the

corresponding curve to the theoretical bound (32) is simply represented by a horizontal line which intercept with the coordinate axis depends upon the relative density (see Figure 9(a), Fiugre 10(a)). From the standpoint of the YDHM, this line delimits from the outside the effective yield surface of the consolidated material powder under consideration.

4.2. Second Proposed Class of Virtual Velocity Fields

Hereafter, one follows the same procedure as in the foregoing analysis but considering a second relevant class of virtual velocity field displayed in Figure 3. is defined by

(33)

where both and are constants to be determined. After some lengthy but straightforward calculations it is found that the polar equations of the failure lines and are respectively given by

(34)

with and

(35)

with and. The parameter sets the geometry of the considered class of failure mechanisms. Applying again the fundamental inequality (16) results in:

(36)

with

(37)

and

(38)

Inequality (36) combined with Equations (37) and (38) may be rearranged in order to provide the following upper bound solutions for

(39)

where, for the sake of conciseness, the expression of the function is not written down herein. In the same manner for failure mechanism, the numerical minimization of with respect to, with, allows to obtain the best upper bound solution, considering the class of virtual velocity fields:

(40)

Figures 4-5 show the third and forth proposed relevant virtual failure mechanisms. The failure mechanisms again exhibit three zones within Ω and contributions to the maximum resisting power are developed inside volumes of zones  and ‚, and along the displayed three velocity jump surfaces, and; the zone ƒ is motionless. For the sake of brevity, the details of calculations corresponding to the application of the fundamental inequality (16) are not repeated herein; one settles for giving the corresponding results which are shown in Figures 9-10.

5. Finite Element Analysis

Suitable FE simulations allow to highlight the deformation mode of the chosen unit cell model as well as to obtain the overall stress-strain curves that represent the behavior of the powder compact at the macroscopic scale. The analysis presented hereafter is similar to Ogbonna and Fleck’s studies [15] where, in particular, the nature of contact growth and material flow based on the deformation of a spherical particle subject to combined radial and axial constraints is discussed. The “probing method” is used to determine the size and shape of the macroscopic yield surface for a consolidated material powder with a prescribed relative density. To this goal, the unit cell model is first strained to a prescribed relative density and unloaded to zero macroscopic stress. The so-called precompact that results from this operation is then re-loaded along various prescribed straining path until the point of plastic collapse. Both proportional and nonproportional straining paths may used to generate data for the yield behavior of the unit cell model. The proportional straining paths include the special cases of closed die compaction and isostatic compaction. The nonproportional paths are for uniaxial compression and for radial compression. The locus of macroscopic stresses at the point of plastic yielding gives the shape of the

macroscopic yield surface. In the initial undeformed configuration the axisymmetric unit cell model is a circular cylinder with diameter and height. Invoking the mass conservation law, the relative density is given by

(41)

which initial value is very close to corresponding to a random close package of equi-sized spherical particles. is assumed to be subject to axisymmetric deformations along a prescribed strain path. By virtue of axisymmetry, only one quarter geometry of the unit cell model, drawn in Figure 6, needs to be analyzed. Frictionless rigid plates indenting the solid grain are used to impose the boundary displacement field. As a consequence of the lattice periodicity both rigid plates at and have a uniform normal displacements in coordinate directions and their mutual orientations will be maintained during the whole process of loading. These requirements impose to remain, during the finite strain deformation process, a cylinder which is thus characterized in an arbitrary state by

(42)

where and are the radial displacement of node and the axial displacement of node, respectively, Figure 6. Quadratic axisymmetric elements in Abaqus code has been used. All elements are of the hybrid type to permit modeling of incompressible behavior. The boundary conditions are outlined in Figure 6: zero normal displacement and zero shear traction are prescribed along the bottom surface. The radial displacement vanishes along the axis of symmetry and the curved surface of the particle is traction free. The radial and axial displacements are applied incrementally, on account of the history dependence of the material response. Various loading paths are achieved by giving different values to the ratios of the displacements and for isostatic and closed die consolidated material powders. The powder particles have been assumed to be an elastic, perfectly plastic solid obeying the -flow theory. The material properties used for the simulation are chosen as follows: Young’s modulus, Poisson ratio and uniaxial yield stress. Typical deformed shapes of the particle under applied macroscopic strain state during stage II compaction are shown in Figures 7-8. It is conspicuous from aforesaid figure that the local deformation of the particle may be seen, besides the parameters and, through the sizes of the axial circular contact area (radius) and the radial annular contact area (radius and width).

6. Results and Discussion

The obtained external estimates of effective yield surfaces for stage II consolidated material powder, for both isostatic and closed die consolidated material powders, are shown in Figure 9 and Figure 10 respectively. The relative density has been fixed to and In these figures, the effective yield surfaces are displayed in normalized stress plane of radial stress versus axial stress and also in normalized stress plane of mean stress versus effective stress. The straight line segments of the macroscopic yield surfaces obtained using the kinematic approach refer to activated failure mechanisms. The obtained results are compared with the numerical ones provided by FE analysis which procedure has been outlined previously. They suggest the following comments.

・ The shape and the size of effective yield surfaces, for both isostatic and closed die consolidated material powder, change as the relative density change between 0.90 and 0.95. As expected, higher the relative density bigger the size of the yield surface.

・ For both values of used in the analysis, it seems that a corner exists at the loading point corresponding the loading path used to derive the powder consolidated material powder.

・ For a given relative density, the yield stress in uniaxial yield compression is lower for isostatic consolidated material powder than for closed die one. The results are opposite for the yield stress in pure radial compression. This observation apparently confirms the fact that the yield behavior of a particle is not just a function of the relative density but also depends on the loading history.

・ The results provided by the kinematic approach is adequate with the finite element predictions that is taken as the reference solutions for the determination of macroscopic yield criteria. Differences can be attributed to the fact that the assumed geometries of unit cells are slightly different for both methods since the size contacts for both methods are in some degree different. It should be kept in mind among other from analysis developed in section 5 that under isostatic compaction, the contact radius increases more than the contact width with increasing relative density for the finite element analysis.

The corpus of the obtained results should necessarily be enriched by lower bound solutions or, even better, by experimental results, since these results are upper bound solutions and they are thus found on the unsafe side of the design. Pastor et al. [17] has provided very close lower and upper bounds of the famous Gurson model used in ductile failure of materials. The methodology employed by these authors comes just at the right moment to address the problem under consideration with however various complexities such as, for example, composite powders. Brown and Weber [18] has demonstrated that the yield behavior of compacted and then sintered powder is different from that of identical powder compacted without sintering, and the uniaxial tensile yield stress is lower for the compacted-only powder. In addition, the Brown and Abou-Chedid's experimental results [19] proved that relative density and particle hardening are not the only state variables to represent powder yield behavior. In this context, the kinematic approach of the yield design theory could turn out to be useful in accounting for the interparticle-cohesion.

7. Conclusion

Based on the kinematic approach of the yield design homogenization method, optimal external estimates of effective yield surfaces of stage II powder compact materials under isostatic and closed die compaction have been obtained. To this goal, an appropriate unit cell model and four relevant failure mechanisms are considered. For comparison purposes, numerical simulations based on FEA similar to those of Ogbana and Fleck [15] have also been carried out. Several interesting conclusions may be drawn.

・ First, the obtained external estimates of the effective strength criteria of the powder compacts at hand may be used either as a rigorous upper bound, or to assess the quality of existing models for yielding of powder compacts during stage compaction II.

・ Compared to the results provided by the FEA, the external estimates of the effective yield surfaces could be deemed to be acceptable from a practical point of view.

・ As expected, their shape and size are found to be dependent on the relative density and on the loading history as well.

・ The results has revealed the existence of a corner on the effective yield surfaces at the loading point.

・ The analysis presented herein may easily be extended to more complex situations than that selected in this paper for illustrative purposes (e.g., consideration of additional classes of failure mechanisms is required, composite powders compacts, accounting for the interparticle-cohesion).

Cite this paper

LarbiSiad,SophieGangloff, (2014) Effective Yield Strength for Material Powder Consolidated at Stage II Compaction. World Journal of Mechanics,04,273-288. doi: 10.4236/wjm.2014.49028

References