ABSTRACT

Several aspects related with Lorentz force are discussed in the light of the presence of vibrating strings. Strings are considered as a compact, tension and viscosity-free incompressible liquid. The motion of a charge particle, obviously, represents the “line of vortex” in the medium of fluid. The term (VXB) turns out to be the natural consequence of Vortex dynamics. The present investigation also reveals the nature of the magnetic field and explains why and how this additional term takes part in Lorentz force.

Keywords:Lorentz Force, Origin for Magnetic Field, Fluid Dynamics, String Theory

1. Introduction

The electromagnetic force related with a moving charge in a simple way is expressed by Lorentz force given by 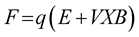[1] :

(1)

where 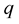is the charge, is the velocity with which the charge particle is moving and 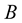is the magnetic field which is associated with the moving charge. This equation does not take into account the distribution and the magnitudes of the other charges present in the system. Equation (1) is based on experimental observations and it holds perfectly in several situations. However, a basic consideration for understanding the mechanism for how and why 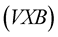term is added in the Equation (1) is needed. The purpose of the present investigation, therefore, is to provide fundamental aspects about the correlation between a moving electric charge and the magnetic field which originates it.

Recently, fundamental aspects of electricity and magnetism are discussed with the help of the presence of vibrating strings [2] [3] . This view also explains the mechanism of electrostatic repulsion and attraction. All the aspects of string theory (like multiple dimensions, tension in the strings and other debatable issues) are not involved in the development of the present theory, but it is only assumed that the space is filled with vibrating strings in a compact, incompressible and non viscous form of liquid. Hence, basic principles of fluid dynamics are employed and the precise mechanism for attraction or repulsion of electric charges is explained satisfactorily [3] . Moreover, it turns out that Maxwell’s equations and other properties of electromagnetic fields are direct consequences of fluid dynamics [2] [4] [5] as the basic concepts and equations are similar. In this context, the liquid is considered as an Eulerian type. The flow quantities are explained only by their position in space and time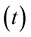, so that the velocity vector can be written as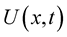. This is unlike Lagrangian type where the flow quantity is also a function of the type of the liquid at a different space (non homogeneity). The application of an Eulerian type supports the view presented earlier [2] [3] .

Research reveals that vacuum is not an empty space but consists of vibrating elements which carry energy and attempts have also been made to convert it into electromagnetic fields [6] -[8] . A close relationship between vacuum energy and electrodynamics has been extensively discussed [8] . Casimir effect [9] confirms the presence of zero point energy of quantized field. Very recently it has been found [10] that heat vibrations escape through ultra high vacuum indicating the presence of some kind of material which is sensitive to vibrations. In such situation, the presence of charge is acting as a source of vorticity in the fluid and its motion is similar to a “vortextube” of infinitesimal diameter. Naturally, the fluid velocity and details of the motion need to be examined with the help of fluid dynamics [4] .

2. Fluid Dynamics

Many fundamental aspects of electricity and magnetism, their correlation and the conservation of charge of the electron etc have been discussed successfully assuming the presence of strings in the form of a compact incompressible liquid [2] . In the present context, we assume that the spin of the charge particle (e.g. electron) acts as a source for vorticity in a liquid only near the line of vortex.

The velocity distribution and the other consequences of vorticity, like expansion, rotation etc., have been discussed extensively [4] . According to fluid dynamics, vortex creates two types of velocities: rotational and irrotational. In the present context we will address only the relevant part namely rotational velocity. As there is a rotational motion of vortex, the fluid velocity in its vicinity can be expressed as [4] :

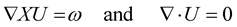(2)

And therefore,

(3)

where 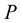is the associated potential Equation (2) becomes:

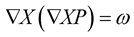(4)

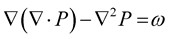(5)

Since, the divergence of potential, 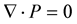everywhere:

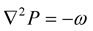(6)

The solution of Equation (6) is given by [4] :

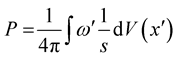(7)

Here the volume integral is taken over an extensive region and s is the magnitude of the vector where 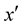denotes the point of interest of evaluation of the potential in the fluid.

The above equation is similar to the potential originated from the wire carrying the current. The magnitude of the current is replaced by the term as both act as vortices in their respective medium.

With the help of Equations (3) and (7) the velocity 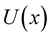near the vortex can be written as [4] :

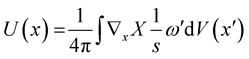(8)

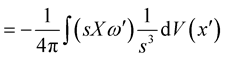(9)

Here, 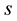is the unit vector and the velocity 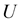can be considered as a vectorial contribution from the different volume elements of the strings in the compact form of the fluid.

When the charge is moving with a certain velocity, the vortex tube is formed in the closed neighborhood of the trajectory of the charge and it is assumed that the fluid is at rest at infinity. It can be considered that vorticity is zero except very close to the vortex tube which can be reduced to the line of vortex and in this process the strength or the intensity, of the vortex tube does not alter.

If 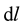is a vector element along the vortex line and it is located in the volume element dV of the closed curve of integration; then the intensity of the “ line vortex” which is responsible for the extra force is given by [4] :

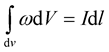(10)

The solenoid velocity distribution originated from the existence of a single line vortex and its associated intensity, can be expressed:

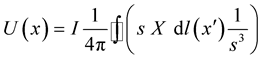(11)

This rotational motion with velocity 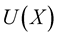provides thrust to the charge. Therefore, the intensity also depends upon the amount of organized strings which presents rotational velocity near the line of vortex. This means that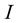, has tensor characters.

When the velocity in the fluid under the presence of vorticity is considered, the effect of velocity of the constituent element is strongly localized near the line of vortex and the contribution from the other parts of the liquid has practically no effect. Thus, the vortex dynamics explains why the force associated with the velocity of the charge takes into account only the magnetic field associated with it. The distribution of other charges does not have a substantial effect and hence the Lorentz force does not take this into account.

3. Discussion

Now, let us consider that the charge particle is moving with velocity, in the electric field. As mentioned earlier, this situation is similar to the motion of the fluid induced by the vortex line. This approach is not new and it was presented long back by Maxwell [11] . He explained several aspects of the magnetic field (or magnetic lines of forces) like pressure and tension by considering the “flow in a fluid” or the motion in a medium. He took into account the molecular vortex to explain several magnetic phenomena.

In the present case, the moving charge creates a circulatory motion of the fluid very close to the vortex line which is explained with the help of Equation (9). Obviously, the force introduced in the system will have cross product with velocity.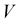

The exact mechanism and origin for the rotational motion and its relation with the magnetic field can be understood with the help of vortex dynamics. In a disturbed or non steady state of liquid originated from the vortex of a moving electron, one portion of the liquid exerts a force on the other portion of the liquid. Extensive analysis of the relative motion near a point of perturbation has been carried out earlier [4] [5] . It is found that there exist three types of motions. One is a uniform translation, the other is a straining in which the rate of the strain tensor decomposes and an isotropic expansion is formed in a compressible liquid in which case a slight variation in volume is observed. This is not possible in the present system as the liquid is incompressible. In this case, the strain is created by the vortex and the corresponding antisymmetric tensor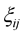, is given by 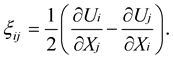[12] :

(12)

Here 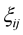is a covariant tensor which is expressed as the gradient of velocity,.

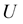This is a rotational motion which provides a force proportional to 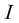and it is assisted by the medium. The above point of view strongly supports the present approach namely the vacuum consists of vibrating strings [6] and the rotational motion is related with the magnetic field [2] . Further, the moment of inertia corresponding to the rotational motion is also possible to calculate. However, in the present case, the parameters related with strings (such as density) are not known. A detail investigation in this direction is badly needed to throw light on the fundamental properties of strings.

As mentioned earlier, the space is filled with strings with density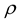. The mass of the total number of strings, shifted per unit time in an organized rotational manner to follow the line of vortex caused by the motion of the charge is given by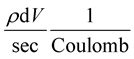. Then the dimensions of the intensity 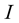related with the vortex line, turns out to be:

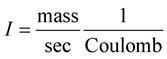(13)

This has exactly the dimensions of the magnetic field and that is why the term added in the Lorentz force has the component of the magnetic field.

The above discussion suggests that the presence and the flow of vibrating strings are the cause for the force and the creation of an additional energy. This means that part of the energy is used from the vacuum. The present analysis directly supports the earlier extensive work [3] [6] [8] [13] related with the extraction of energy from the vacuum, including a patent [13] . This aspect needs further investigation from the point of view of direct application.

4. Conclusions

In short, the velocity with which the charge particle is moving creates the rotational velocity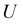, in the compress liquid of strings. The intensity of the rotational motion turns out to be the magnetic field. Therefore, an extra force (per unit charge) of the magnitude 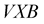is created and this is reflected in the experimentally observed “Lorentz equation”.

The present analysis not only strongly supports the presence and the role of vibrating strings in association with electric and magnetic fields but also helps to understand how and why the magnetic field is created with the moving charge and contributes in Lorenz force.

References