World Journal of Mechanics
Vol.4 No.6(2014), Article
ID:47445,4
pages
DOI:10.4236/wjm.2014.46017
Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity
Mohamed El Naschie
Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2014; revised 15 April 2014; accepted 12 May 2014
ABSTRACT
We determine the limit of the ratio formed by the independent components of the Riemann tensor to the non-zero component as space dimensionality tends to infinity and find it to be 12. Subsequently we use this result in conjunction with Newtonian classical mechanics to show that the ordinary measurable cosmic energy density is given by 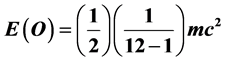 while the dark energy density is obviously the Legendre transformation dual energy E(D) = 1 ‒ E(O). The result is in complete agreement with the COBE, WMAP and type 1a supernova measurements.
while the dark energy density is obviously the Legendre transformation dual energy E(D) = 1 ‒ E(O). The result is in complete agreement with the COBE, WMAP and type 1a supernova measurements.
Keywords:Semi Classical Quantum Systems, Dark Energy, Accelerated Cosmic Expansion, Riemannian Tensor, Infinite Dimensional Topology, Nonlocal Elasticity

1. Introduction
The present analysis, although quite short and straight forward, is never the less of considerable importance to the understanding of arguably one of the most difficult questions presently facing both theoretical physics and cosmology, i.e., the meaning and nature of dark energy [1] -[8] . Unlike previous publications we concentrate here on taking the limit of infinite dimensional geometry and proceed from there, using Newtonian mechanics only, to show that the analysis and results are consistent with a physical truly fractal and Cantorian spacetime [4] -[10] . Finally we hint at a connection to nonlocal elasticity [11] -[13] .
2. Analysis
In the following short communication we employ what is essentially a fractal spacetime picture to compute the dark energy density [1] -[10] via the ratio of non-zero components [1] to the total number of independent components in n dimensions when we let n tend to infinity. We recall that voids in spacetime are essentially empty sets with a negative Menger-Uhryson topological dimension while ordinary spacetime are zero sets [10] . Said in the language of fractals, empty regions are fat fractals while non-empty regions of spacetime are thin fractals [4] -[10] . Translated to the algebraic geometry of a Riemannian tensor, the ordinary spacetime regions are represented by the non-zero component of the tensor in n dimensions which are given as is well known by [1] :
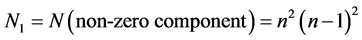 (1)
(1)
On the other hand the total numbers of independent components are given by the well known Formula:
 (2)
(2)
Following what we reasoned earlier on then we can regard the sparsity ratio N2/N1 as essentially the Lorentzian factor in Einstein’s Formula [7] -[10] . That means we regard  as the regular hundred percent total energy density which is a basic tacit assumption in all our non-fractal theories in high energy physics and cosmology. Consequently Newton’s kinetic energy [4] -[10] :
as the regular hundred percent total energy density which is a basic tacit assumption in all our non-fractal theories in high energy physics and cosmology. Consequently Newton’s kinetic energy [4] -[10] :
 (3)
(3)
could be thought of as a generalization of Einstein’s energy when v → c and  → 1 [10] . This limit corresponds in set theoretical formulation to when the zero set
→ 1 [10] . This limit corresponds in set theoretical formulation to when the zero set 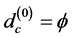 changes its average value
changes its average value 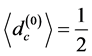 and tends to the unitary set
and tends to the unitary set  [10] . Following this transfinite set theoretical logic we can write [5] -[8] :
[10] . Following this transfinite set theoretical logic we can write [5] -[8] :
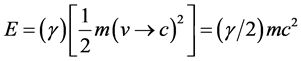 (4)
(4)
On the other hand for a Cantorian fractal formal dimensionality is intrinsically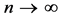 . Therefore by letting n go to infinity and using the role of de L’Hopital we have [1] :
. Therefore by letting n go to infinity and using the role of de L’Hopital we have [1] :
 (5)
(5)
Inserting in E we find the following slightly inaccurate result as will be explained later [4] -[10] :
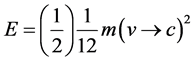 (6)
(6)
Now a direct comparison between E = mc2 and E(0) could not be made unless we become completely aware that E = mc2 was tacitly based on a one degree of freedom Lagrangian which Einstein never wrote down. This is of course the U(1) single photon degree of freedom leading to E = mc2. The above formula however has taken on board also indirectly 12 degrees of freedom 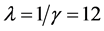 representing the 12 messenger photons of the standard model, i.e., |SU(3)| = 8 gluons, |SU(2)| = 3 (
representing the 12 messenger photons of the standard model, i.e., |SU(3)| = 8 gluons, |SU(2)| = 3 (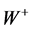 ,
,  ,
, ) and |(U)| = 1 photon [10] . Consequently consistency requires us to subtract the ordinary photon from our 12 messenger particles so that we do not double count it. In other words we have the following consistent limits:
) and |(U)| = 1 photon [10] . Consequently consistency requires us to subtract the ordinary photon from our 12 messenger particles so that we do not double count it. In other words we have the following consistent limits:
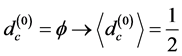 (7)
(7)
 (8)
(8)
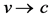 (9)
(9)
 (10)
(10)
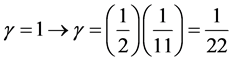 (11)
(11)
That way we find the correction  and thus:
and thus:
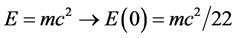 (12)
(12)
From the above the dark energy density is easily deduced to be [4] -[10] :
 (13)
(13)
which is 95.5% of the total energy in full agreement with measurements as well as previous theoretical derivations. We could validate the preceding result in virtually one line of analysis when we consider that the only non-zero components of the Riemann tensor of general relativity is 24 [1] and compare that with the maximal possible of symmetries as given by the killing vector fields of Witten’s 5 Brane theory in eleven dimensions, namely 528. The ratio  is then given in a trivial straight forward way by [4] -[10] :
is then given in a trivial straight forward way by [4] -[10] :
 (14)
(14)
exactly as shown above. Dark energy density is consequently [5] -[8] :
 (15)
(15)
also as shown above.
3. Conclusion
In the present short analysis we started from an infinite dimensional geometry and topology and ended with a finite expression for both the ordinary and the dark energy density of the cosmos. The result, as expected, is in full agreement with measurements but we gained additional evidence for the true physical fractality of spacetime at both the quantum as well as the cosmological level [1] -[10] . It is crucial to appreciate the deep meaning and implications of obtaining a quantum gravity result in agreement with cosmic measurements using essentially Newtonian classical mechanics and without involving quantum mechanics. We stress that this is only possible because of our use of nonclassical fractal-Cantorian spacetime geometry and infinite dimensional topology [4] -[10] . We note on passing that we have very recently discovered that all the above results could also be obtained using the nonlocal elasticity theory of A. C. Eringen [6] [11] -[14] which is a welcome confirmation of the basic philosophy of the present work, namely the unity of physics, mathematics, engineering and philosophy [14] .
References
- Martin, J.L. (1995) General Relativity. Prentice Hall, London. in particular pages 89 and 111.
- Linder, E. (2008) Dark Energy. Scholarpedia, 3, 4900. http://dx.doi.org/10.4249/scholarpedia.4900
- Caroll, S. (2013) Why Does Dark Energy Make the Universe Accelerate? http://www.preposterousuniverse.com/blog/2013/11/16/why-does-dark-energy-make-t
- El Naschie, M.S. (2014) Calculating the Exact Experimental Density of the Dark Energy in the Cosmos Assuming a Fractal Speed of Light. International Journal of Modern Nonlinear Theory and Application. in press.
- El Naschie, M.S. (2014) Cosserat-Cartan and de Sitter-Witten Spacetime Setting for Dark Energy. Quantum Matter. in press.
- El Naschie, M.S. (2014) Pinched Material Einstein Spacetime Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90. http://dx.doi.org/10.4236/ijaa.2014.41009
- El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological in Terpretation. Gravitation and Cosmology, 19, 151-155. http://dx.doi.org/10.1134/S0202289313030031
- El Naschie, M.S. (2014) Dark energy via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
- El Naschie, M.S. (2013) Experimentally Based Theoretical Arguments that Unruh’s Temperature, Hawking’s Vacuum Fluctuation and Rindler’s Wedge Are Physically Real. American Journal of Modern Physics, 2, 357-361. http://dx.doi.org/10.11648/j.ajmp.20130206.23
- El Naschie, M.S. (2013) Quantum Entanglement: Where Dark Energy and Negative Gravity Plus Accelerated Expansion of the Universe Comes from. Journal of Quantum Information Science, 3, 57-77. http://dx.doi.org/10.4236/jqis.2013.32011
- Eringen, A.C. and Edelen, D.G. (1972) On Nonlocal Elasticity. International Journal of Engineering Science, 10, 233-248. http://dx.doi.org/10.1016/0020-7225(72)90039-0
- Challamel, N., Wang, C.M. and Elishakoff, I. (2014) Discrete Systems Behave as Nonlocal Structural Elements; Bending Buckling and Vibration Analysis. European Journal of Mechanics—A/Solids, 44, 125-135. http://dx.doi.org/10.1016/j.euromechsol.2013.10.007
- El Naschie, M.S. (1990) Stress, Stability and Chaos in Structural Engineering: An Energy Approach. McGraw Hill, London.
- El Naschie, M.S. (2014) The Meta Energy of Dark Energy. Open Journal of Philosophy. In press.

