World Journal of Mechanics
Vol.4 No.7(2014), Article
ID:47754,7
pages
DOI:10.4236/wjm.2014.47021
Numerical Investigation of Bismuth Unloading Solidification with Abnormal Melting Characteristic
Jingsong Bai1,2, Jidong Yu1, Tao Wang1*
1Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang, China
2National Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang, China
Email: *wtao_mg@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 25 February 2014; revised 21 March 2014; accepted 14 April 2014
ABSTRACT
We present the processes and results of a numerical investigation of the bismuth unloading solidification by a graded density impactor, and demonstrate that the physical process may be realized due to bismuth abnormal melting characteristics. A more reasonable high-pressure solid equation of state of the fifth phase bismuth is introduced in our calculation and one type of graded density impactor made of 15 compositions of Mg-Cu material system is given in this paper. We detailedly investigate one possible proposed approach to achieve the unloading solidification physical process, and our numerical analysis on the thermodynamic state, the unloading path and the phase transformations.
Keywords:Unloading Solidification, Graded Density Impactor, Phase Transformations

1. Introduction
Bismuth in the solid state has many kinds of metal states. It is at a low pressure and temperature range of memory in a series of multi physiognomy phase transition. Bismuth in the impact dynamics of this feature has caused widespread concern of researchers. Many scientists on the shock induced phase transition of bismuth carried out a large number of theoretical and experimental researches. Bridgman [1] first measured bismuth’s static pressure data, and then the static pressure measurement data obtained by other subsequent scientists [2] -[4] are in good agreement with the Bridgman’s. Duff [5] and his collaborators first studied the shock induced phase transition of bismuth. They used two kinds of techniques of explosive load and electrical probe measurement speed, observed bismuth’s phase transition from the solid phase I to solid phase II in the experiment, but the phase transition pressure is about 0.25 GPa higher than the static pressure. In addition, they failed to observe the transition of bismuth from solid phase I to liquid phase. Larson [6] used a kind of quartz probe velocimetry to study the shock induced phase transition of bismuth from the solid phase I to solid phase II, and obtained good agreement with the static high-pressure phase transition pressure. Asay [7] [8] obtained a higher resolution waveform profile in the light gas gun experiment by applying the VISAR technology than Larson, and he studied the two kinds of phase transition of bismuth from solid phase I to solid phase II and solid phase I to liquid phase more completely, and the measured phase transition pressure of bismuth from solid phase I to solid phase II is consistent with the result of Larson and the measured static pressure. The temperature-pressure phase diagram of bismuth has been the subject of many studies, which will undoubtedly continue [9] [10] . The slope of the melting curve below 1.7 GPa is less than zero, and this abnormal melting character will result in the possibility of the resolidification under unloading. Streitz [11] succeeded in the investigation of bismuth resolidifying from a molten sample to a high pressure solid state by applying the isentropic compression profiles of the graded density impactor (GDI). A schematic phase diagram of bismuth with an isentropic displays the pathway of resolidification in Figure 1. A solid bismuth system is heated and melted to point A; the liquid is then compressed along its isentropic to point B; the fusion heat contained in the system is released as it undergoes a first-order phase transition until C, from which the solid bismuth is isentropically compressed to its final state D.
We are motivated by the interesting investigation of the unloading solidification of bismuth by using a GDI due to bismuth abnormal melting characteristic, and try to find one possible approach to achieve the physical processes. From the Figure 1, we can see that the abnormal melting curve of the bismuth is very limited in the low-pressure section (E → F). To our knowledge, whether it is in numerical or in experimental studies has not been reported in the literature. In this paper, we first give how the physical process is achieved numerically. Considering the abnormal feature of melting curve, one possible approach is proposed to realize the physical process, which is the impact loading and unloading to melting of solid phase bismuth and subsequent unloading solidification in liquid region. As the GDI’s features, such as the loading speed, etc., may affect the unloading path of bismuth in the liquid region, in order to achieve the unloading solidification of bismuth in the liquid region, we must carefully design the physical model. For achieving the research we developed a one-dimensional elastic-plastic fluid dynamics program, which includes the calculation of phase transformation kinetics.
2. Improved High-Pressure Solid Equation of State
The bismuth equation of state (EOS) in this paper contains five solid phases and a liquid phase. According to the Johnson’s research [12] , the Helmholtz free energy of i-phase is written as:
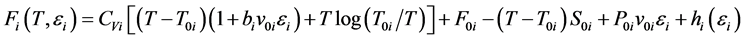 (1)
(1)
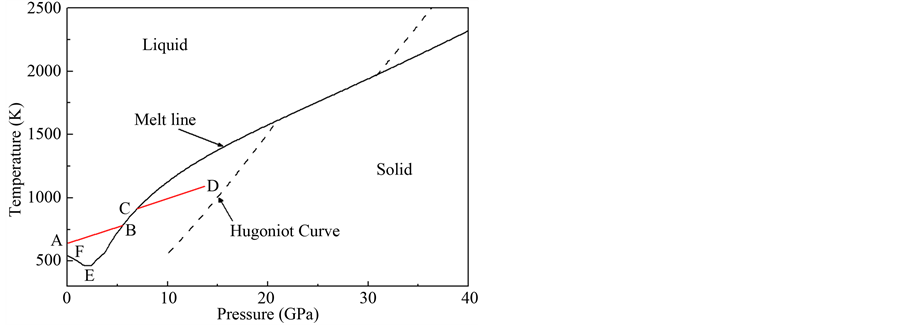
Figure 1. A schematic phase diagram of bismuth with an isentrope pathway to resolidification.
 and
and 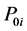 are the reference temperature and pressure of the i-phase.
are the reference temperature and pressure of the i-phase.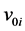 ,
, 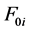 and
and  are respectively the specific volume, Helmholtz free energy constant and entropy constant. cvi is the specific heat at constant volume.
are respectively the specific volume, Helmholtz free energy constant and entropy constant. cvi is the specific heat at constant volume.  is the volume strain.
is the volume strain. 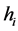 is a function of
is a function of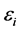 , and has the following three different forms:
, and has the following three different forms:
(a) When the isothermal bulk modulus 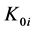 is constant,
is constant,
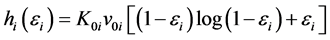 (2)
(2)
(b) When the isothermal bulk modulus is a linear function of pressure
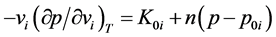
where n is nondimensional constant;
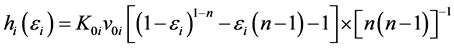 (3)
(3)
(c) For Solid phase I,
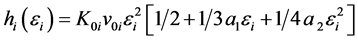
parameter a1, a2, and K0i can be obtained from Hugoniot date.
For solid phase II, III, IV, the isothermal bulk modulus is assumed to be constant, and the EOS parameters can be obtained from reference [12] [13] . For solid phase V, this assumption is not appropriate at high pressure, so we consider the isothermal bulk modulus is a linear function of pressure, and EOS parameter is chosen so that the phase boundary between solid phase V and liquid phase can reproduce the Pelissier melting curve [14] . Therefore a more reasonable high-pressure solid phase V EOS is introduced in our calculation. The EOS parameter is shown in Table 1, and the calculated temperature and pressure phase diagram is shown in Figure 2.
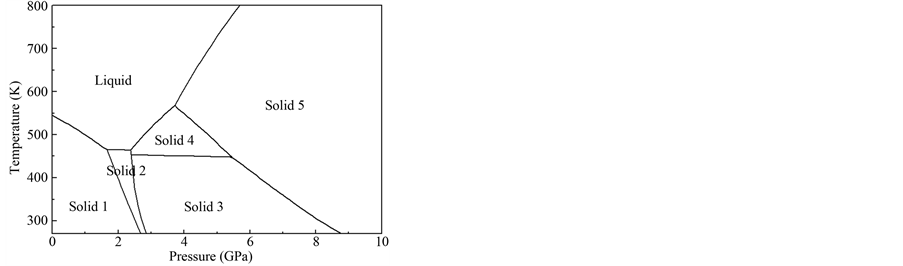
Figure 2. A schematic phase diagram of bismuth in our calculation, include five solid phases and a liquid phase situations.
Table 1. Phase parameters of equation of state of bismuth in our calculation.
3. Results and Analysis
A configuration of the light gas gun experiment device may used to be achieved the physical process, which is shown in Figure 3. The layered impactor may increase the flexibility in designing applied-pressure profiles through various combinations of shock, quasi-isentropic compression, controlled release, and constant pressure. Therefore they can remove some significant constraints on the thermodynamic path. The evolution of the pressure experienced by the target materials can be “tailored” by appropriately designing the density profile, thickness, or rather the shock impedance profile of the impactor, but it is very difficult to achieve this goal by using homogeneous impedance impactor in a single experiment. The particle velocity profiles of target materials can be measured by VISAR [15] (Velocity Interferometer System for Any Reflector) or DISAR [16] (Displacement Interferometer System for Any Reflector) in gas-gun experiments. In this paper, one type of GDI made of 15 compositions of Mg-Cu material system is given by using the theoretical analysis and numerical computation to study the physical process of bismuth unloading solidification. The GDI material density of each layer changes according to the second power, and impact 1.5 mm bismuth sample and 10 mm LiF window. The highest impedance of the GDI is 100% copper, the lowest impedance is 100% magnesium, and the middle part is the mixture of Mg-Cu material system with different mass percent. From magnesium to copper, the density of impactor changes according to the relationship ρ = ρ0 + Axp, and p = 2, ρ0 = 1.74 g/cm3, A = 1.629 (g/cm3)/mm3. The first layer of material copper with the thickness of 0.4mm impacts directly bismuth, the thickness of the remaining 14 layers is 0.15 mm for each one. Then the total thickness of GDI is 2.5 mm.
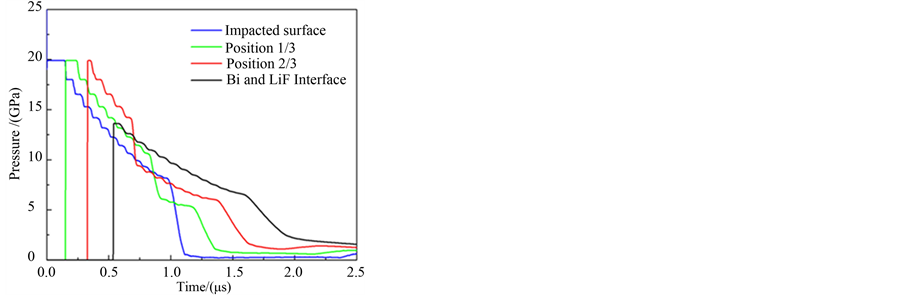
In our numerical simulation, we set the initial impact velocity of GDI as 1.2 km/s. In order to analyze the physical state of bismuth sample, we give the pressure and particle velocity history profiles at four characteristic positions which are the impacted surface, 1/3 from the impacted surface, 2/3 from the impacted surface and interface between bismuth and LiF window respectively. At the same time, because of the use of phase transformation kinetics model for the entire process, the phase diagram shows the positions of 2/3 from the impacted surface and the interface between bismuth and LiF window, and the corresponding states of thermodynamic path. Figure 4 shows the pressure and particle velocity history at four positions in bismuth sample when the GDI impacts bismuth with 1.5 mm thick and LiF with 10 mm thick at 1.2 km/s. We can see that the width of first step of pressure and velocity profile decreased, and the particle velocity of four locations in bismuth sample increased significantly. The lower initial impact velocity caused the lower pressure on shock front and velocity on impacted surface. The reason causing the first phenomenon is that the impedance of the first layer of GDI with 0.4 mm copper is the highest, other layers have the same thickness of 0.15 mm and their impedance decreases gradually, the continuous unloading of rarefaction wave makes the shock front to narrow gradually, the front pressure at the position of 2/3 from impacted surface will be lower than the ones at impacted surface. For the second phenomenon, the reason is that the impedance of LiF window is smaller than bismuth, and an unloading wave propagates into the bismuth sample continuously, and causes the pressure at the internal position of bismuth where the unloading wave arrives decreasing quickly and the particle velocity increasing. Figure 5 shows thermodynamic state, the unloading path beginning with the corresponding state and the mass composition of liquid phase at the two characteristic positions within the sample. In our calculated results, it is shown that the the

Figure 3. A configuration of the experimental device of unloading solidification of bismuth loaded by a graded density impactor.
 (a)
(a)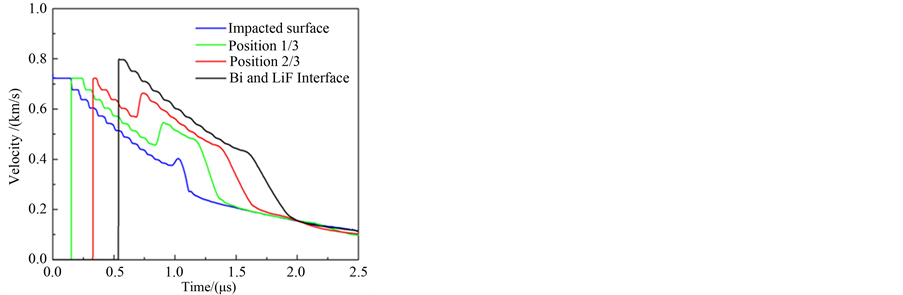 (b)
(b)
Figure 4. Pressure and particle velocity profiles at four positions in bismuth sample when initial impact velocity of 1.2 km/s.
 (a)
(a)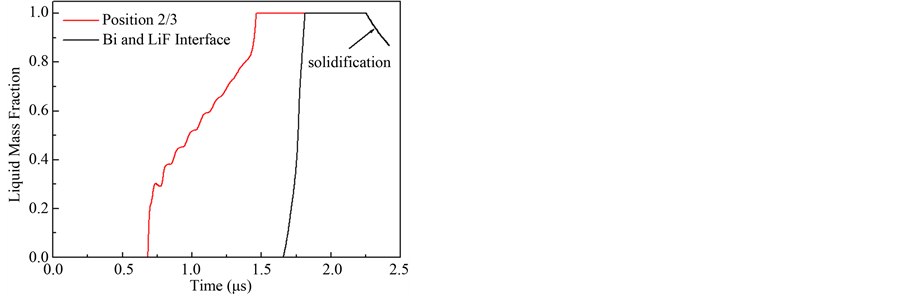 (b)
(b)
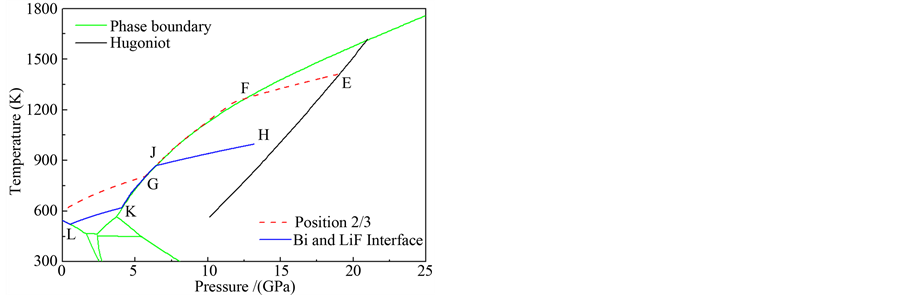
Figure 5. Calculation gives the thermodynamic state and unloading path of the two characteristic positions in phase diagram.
unloading solidification of bismuth is achieved at the position of bismuth and LiF window, and the unloading path H → J → K → L finally intersects with the abnormal melting curve again. It is can not be realiazed for unloading solidification along the unloading path E → F → G at at the position of 2/3 from the impacted surface. From the Figure 5(a), we can see that the unloaded state (state H) of the interface between bismuth and LiF window does not locate on shock Hugoniot line (shown in Figure 5(a)). The unloading path along H → J and state J with pressure 6.40 GPa and temperature 868K lie in solid-liquid mixing region. When the pressure and temperature reduce to 4.05 GPa and 618 K (state K), the solid bismuth in mixing region completely melted. The next unloading is carried out in liquid phase. When the pressure and temperature reduce to 0.53GPa and 522 K (state L), the unloading line intersects with the solid-liquid melting ling again. We finally see that the latest unloading solidification appears in mixing phase, which is shown as the black line in Figure 5(b). For the another position of 2/3 from the impacted surface, the state E with pressure 19.45 GPa and temperature 1420 K locates on the solid shock Hugoniot line. The state F along with unloading path E → F lies in solid-liquid mixing region with pressure 11.97 GPa and temperature 1251 K. Then the unloading-melting in mixing phase appeared. When the pressure and temperature reduce to 5.67 GPa and 804.2 K (state G), the solid bismuth in mixing region completely melted. Subsequently, the latest unloading is carried out in liquid phase. This is evident from calculation of the liquid phase mass fraction (red line in Figure 5(b)). It is obvious that the unloading solidification cannot be achieved at the internal position of 2/3 from the impacted surface at the initial impact velocity 1.2 km/s of GDI.
In addition, another approach, which is the impact melt of solid bismuth and subsequent unloading solidification in liquid region and the initial impact velocity of GDI is set as 2.5 km/s and 1.8 km/s, is analyzed numerically. Figure 6 shows the calculated thermodynamic state and path of two characteristic positions in phase dia-
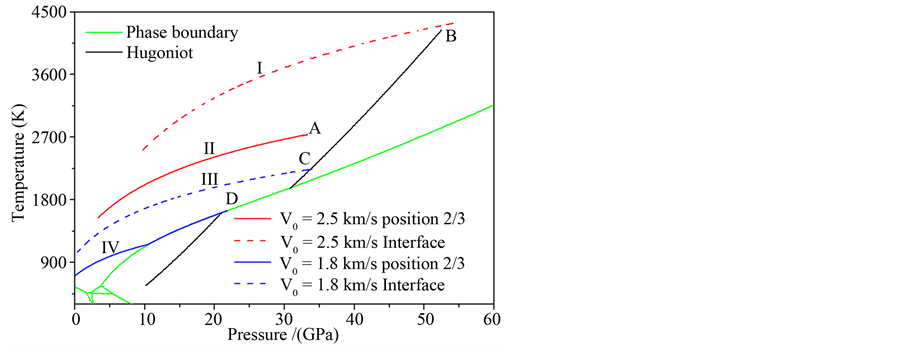
Figure 6. Calculation gives the thermodynamic state and unloading path of the two characteristic positions in phase diagram.
gram at two loading speeds. We found that the unloading path in bismuth will not intersect with the melting line, and the unloading solidification physics process cannot be appeared.
4. Conclusion
In conclusion, our investigation demonstrates that bismuth may be resolidificated under unloading due to its abnormal melting characteristics, and an approach was found to achieve the physical process successfully. A more reasonable high-pressure solid equation of state of the fifth phase bismuth is introduced in our calculations. One type of GDI made of 15 compositions of Mg-Cu material system is designed as the driving flier. The pressure and particle velocity history profiles of impacted surface, 1/3 from the impacted surface, 2/3 from the impacted surface and the interface between bismuth and LiF window are detailedly analyzed. We identify the thermodynamic state and unloading path of the impacted surface and interface between bismuth and LiF window in phase diagram. Although we found the realization of the physical process of one possible way, but considering the limitation of the abnormal melting region, it still faces many technical difficulties for measuring the process in experiments actually.
Acknowledgements
The research was sponsored by the National Science Foundation of China Grant No. 11372294 and 11202195, the Science Foundation of China Academy of Engineering Physics Grant No. 2011A0201002.
References
- Bridgman, P. W. (1935) Polymorphism, Principally of the Elements, up to 50,000 kg/cm2. Physical Review, 48, 893-906.
- Bundy, F.P. (1958) Phase Diagram of Bismuth to 130,000 kg/cm2, 500°C. Physical Review, 110, 314-318. http://dx.doi.org/10.1103/PhysRev.110.314
- Klement, W., Jayaraman, A. and Kennedy, G.C. (1963) Phase Diagrams of Arsenic, Antimony, and Bismuth at Pressures up to 70 kbars. Physical Review, 131, 632-637. http://dx.doi.org/10.1103/PhysRev.131.632
- Vereshchagin, L.F., Zubova, E.V., Stupnikov, V.A. and Aparnikov, G.L. (1974) Temperature Dependence of the Hysteresis at the Polymorphic Transitions of Bismuth. High Temperatures-High Pressures, 6, 509.
- Duff, R.E. and Minshall, S. (1957) Investigation of a Shock-Induced Transition in Bismuth. Physical Review, 108, 1207-1212. http://dx.doi.org/10.1103/PhysRev.108.1207
- Larson, D.B. (1967) A Shock-Induced Phase Transformation in Bismuth. Journal of Applied Physics, 38, 1541. http://dx.doi.org/10.1063/1.1709720
- Asay, J.R. (1974) Shock-Induced Melting in Bismuth. Journal of Applied Physics, 45, 4441. http://dx.doi.org/10.1063/1.1663070
- Asay, J.R. (1977) Shock loading and unloading in bismuth. Journal of Applied Physics, 48, 2832. http://dx.doi.org/10.1063/1.324144
- Duvall, G.E. and Graham, R.A. (1977) Phase Transitions under Shock-Wave Loading. Reviews of Modern Physics, 49, 523-579. http://dx.doi.org/10.1103/RevModPhys.49.523
- Yu Tonkov, E. and Pomyatovsky, E.G. (2005) Phase Transformations of Elements under High Pressure. CRC Press, Boca Raton.
- Streitz, F.H., Nguyen, J.H., Orlikowski, D., Minich, R., Moriarty, J.A. and Holmes, N.C. (2005) Rapid Resolidification of Metals Using Dynamic Compression. Final Report 02-ERD-033, UCRL-TR-209674.
- Johnson, J.N., Hayes, D.B. and Asay, J.R. (1974) Equations of State and Shock-Induced Transformations in Solid I-Solid II-Liquid Bismuth. Journal of Physics and Chemistry of Solids, 35, 501-515. http://dx.doi.org/10.1016/S0022-3697(74)80004-1
- Kane, J.O. and Smith, R.F. (2005) Modeling Non-Equilibrium Phase Transitions in Isentropically Compressed Bi. AIP Conference Proceedings, 845, 244.
- Pelissier, J.L., Wetta, N. (2001) A Model-Potential Approach for Bismuth (I). Densification and Melting Curve Calculation. Physica A: Statistical Mechanics and its Applications, 289, 459-478. http://dx.doi.org/10.1016/S0378-4371(00)00514-8
- Fleming, K.J. and Broyles, T.A. (2003) Shock Analysis Using the Multipoint Velocimeter (VISAR). Sandia Report, SAND 2003-3759
- Weng, J. D., Tan, H., Wang, X., et al. (2006) Optical-Fiber Interferometer for Velocity Measurements with Picosecond Resolution. Applied Physics Letters, 89, 111101
NOTES

*Corresponding author.


