World Journal of Mechanics
Vol.04 No.01(2014), Article ID:42190,10 pages
10.4236/wjm.2014.41001
Theoretical Analysis of Mechanical Vibration for Offshore Platform Structures
Saeed A. Asiri1, Yousuf Z. AL-Zahrani2
1MENG Graduate Office, Department of Production and Mechanical Systems Design, Engineering College of King Abdulaziz University, Jeddah, KSA
2Department of Production and Mechanical Systems Design, Engineering College of King Abdulaziz University, Jeddah, KSA
Email: saeed@asiri.net, eng.yousuf@gmail.com
Copyright © 2014 Saeed A. Asiri, Yousuf Z. AL-Zahrani. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Saeed A. Asiri, Yousuf Z. AL-Zahrani. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
A new class of support structures, called Periodic Structures, is introduced in this paper as a viable means for isolating the vibration transmitted from the sea waves to offshore platform structures through its legs. A passive approach to reduce transmitted vibration generated by waves is presented. The approach utilizes the property of periodic structural components that create stop and pass bands. The stop band regions can be tailored to correspond to regions of the frequency spectra that contain harmonics of the wave frequency, attenuating the response in those regions. A periodic structural component is comprised of a repeating array of cells, which are themselves an assembly of elements. The elements may have differing material properties as well as geometric variations. For the purpose of this research, only geometric and material variations are considered and each cell is assumed to be identical. A periodic leg is designed in order to reduce transmitted vibration of sea waves. The effectiveness of the periodicity on the vibration levels of platform will be demonstrated theoretically. The theory governing the operation of this class of periodic structures is introduced using the transfer matrix method. The unique filtering characteristics of periodic structures are demonstrated as functions of their design parameters for structures with geometrical and material discontinuities, and determine the propagation factor by using the spectral finite element analysis and the effectiveness of design on the leg structure by changing the ratio of step length and area interface between the materials is demonstrated in order to find the propagation factor and frequency response.
Keywords
Vibrations Attenuation; Periodic Structures; Offshore Platforms; Periodic Legs
1. Introduction
Offshore construction is the installation of structures and pipelines in a marine environment for the production and transmission of oil and gas (see Figure 1).
Construction in the offshore environment is a dangerous activity and where possibly the construction is modular in nature with the individual modules being assembled on shore and using a Crane Barge to lift the modules into place. Offshore structures can be designed for installation in protected waters, such as lakes, rivers, and

Figure 1.Oil and gas offshore platform.
bays or in the open sea, many kilometers from shorelines. The oil and gas exploration platforms are the best example of offshore structures that can be placed in water depths of 2 kilometers or more. These structures may be made of steel, reinforced concrete or a combination of both. They are more than 6500 offshore installations around the world in 53 countries approximately (see Figure 2). Offshore platforms have many uses including oil exploration and production, navigation, ship loading and unloading, and supporting bridges and causeways. Offshore oil production is one of the most visible of these applications and represents a significant challenge to the design engineer. These offshore structures must function safely for design lifetimes of twenty years or more and are subject to very harsh marine environments. Some important design considerations are peak loads created by hurricane wind and waves, fatigue loads generated by waves over the platform lifetime and the motion of the platform. The platforms are sometimes subjected to strong currents which create loads on the mooring system and can induce vortex shedding and vortex induced vibration [1].
Offshore platforms suffer from different kinds of mechanical vibrations due to exposure to water waves, wind, severe environmental conditions, helicopter landing, impact boats, the intensity level of consequences of failure machinery etc. One of the major sources of such mechanical vibrations on offshore platforms is the impact of sea waves on to the platform’s legs. These mechanical impacts are transferred through the platform’s legs from the bottom up to the highest top end of such a structure, which consist of employee’s offices, accommodations, measurement instruments, piping, and heavy machinery. The aim will be minimized these vibrations on offshore platforms caused by the impact of the sea wave transmission to the offshore platforms through the platform’s leg structure; we try to make a good solution to provide a better isolation of mechanical vibration by using the periodic structure technique [1].

Figure 2. Examples of offshore rigs, drilling and production platforms.
2. Literature Review
The basic idea underlying the whole concept of periodic structures is that when a wave is traveling in a medium and meets a transition in that medium characteristic, part of it will propagate through the new medium and another part will reflect into the old one. In a regular structure the wave is expected to travel without any change until it reaches the boundaries of that structure, but when the structure exhibits a change it its geometry and/or material properties, the incident waves will divide as described before. A part of the reflected wave will interact with the incident wave in a manner that will characterize the interference. When constructive interference occurs, the frequency is characterized by being the pass band of the structure; while, if they destructively interfere, the frequency ischaracterized by being the stop band of the structure. If the structure setup is repeated for several times, it is known a periodic structure. The destructive effects will show more significantly when the repetitions of the structural unit increase in number because as the part of the wave that propagates incorporates other similar changes in the medium, another part of it is destructed and so on.
In his paper reviewing the research performed in the area of wave propagation in periodic structures, Mead [2] defined a periodic structure as a structure that consists fundamentally of a number of identical structural components that are joined together to form a continuous structure. Examples of periodic structures can be seen in satellite solar cells, wings and fuselages of aircraft, petroleum pipelines, railway tracks, and many others. An illustration.
If a simple periodic bar is presented in Figure 3(a) with geometrical discontinuity and Figure 3(b) with material discontinuity.
In general, when a wave propagating in a structure encounters a change in the geometry and/or the material properties, the wave is split into two components; a prop-

Figure 3. Typical examples of periodic structures.
agating component and a reflected component. The reflected part interacts with the propagating part in a manner that is decided by the phase difference between them.
Studies of the characteristics of one-dimensional periodic structures have been extensively reported [1-14]. These structures are easy to analyze because of the simplicity of the geometry as well as the nature of coupling between neighboring cells.
Cremer [15] presented a derivation of an expression that could describe the steady state vibration of an infinite beam uniformly supported on impedances. That formulation allowed for the analysis of the structures with fluid loadings easily. Later, Gupta [16] presented an analysis for periodically-supported beams that introduced the concepts of the cell and the associated transfer matrix. He presented the propagation and attenuation parameters’ plots which form the foundation for further studies of one-dimensional periodic structures. Faulkner and Hong [17] presented a study of mono-coupled periodic systems. Their study analyzed the free vibration of the spring- mass systems as well as point-supported beams using analytical and finite element methods.
Mead and Yaman [18] presented a study of the response of one-dimensional periodic structures subject to periodic loading. Their study involved the generalization of the support condition to involve rotation and displacement springs as well as impedances. The effects of the excitation point as well as the elastic support characteristics on the pass and stop characteristics of the beam are presented. Later, Mead, White and Zhang [19] proved that the power transmission in both directions of a simply supported beam excited by a point force was equal regardless of the excitation location.
The most common damping technique studied in periodic structures was through the introduction of random disorder. The concept of wave localization phenomenon was introduced to the study of mechanical wave propagation by Kissel [20] through the use of the transfer matrix approach. Using the concept of periodic structures, Ruzzene and Baz [21] used shape memory inserts into a one dimensional rod, and by activating or deactivating the inserts they introduced a periodicity which in turn localized the vibration near to the disturbance source. Later, they used a similar concept to actively localize the disturbance waves traveling in a fluid-loaded shell [22]. Asiri et al. [23] emphasized is placed on developing a new class of these periodic structures called active periodic struts, which can be used to support gearbox systems on the airframes of helicopters. When designed properly, the passive periodic strut can stop the propagation of vibration from the gearbox to the airframe within critical frequency bands, consequently minimizing the effects of transmission of undesirable vibration and sound radiation to the helicopter cabin. The theory governing
the operation of this class of passive periodic struts is introduced and their filtering characteristics are demonstrated experimentally as a function of their design parameters. Asiri [24] presented a new class of periodic mounts for isolating the vibration transmission from vehicle engine to the car body and seats. Later, Asiri et al. [25] studied experimentally the dynamic response of offshore platforms with periodic legs while this paper is an analytical study of the same model.
3. A periodic Beam Model
The periodic structures are made of the assemblies of the periodic cells shown in Figure 4. Each of these unit cells consists of two substructures a and b which can be either of the same material with different cross sections Figure 4(a), made of different materials with the same cross section Figure 4(b) and both made of different materials with the different cross sections, Figure 4(c).
For a beam shown in Figure 5, the equation of motion (EOM) may be shown to be considering a beam section with uniform properties
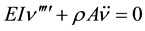 (1)
(1)
Which has the solution
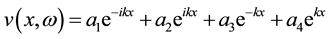 (2)
(2)
The nodal displacements of the element are given by


Figure 4. Unit asymmetric CELLS of periodic structure.
Figure 5. Shaft geometry.
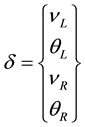 (3)
(3)
The evaluating the solution at the left and right nodes,
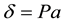 (4)
(4)
In Figure 6, Where ν and θ define the lateral displacement and rotational displacement with subscripts L and R denoting the left and right sides of the cell. Also, F and M define the nodal force and the nodal momentwith subscripts L and R denoting the left and right sides of the cell.
Apply Boundary Conditions to evaluate the P
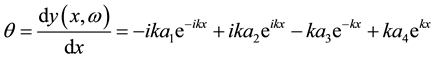 (5)
(5)
 (6)
(6)
The nodal forces and moments are
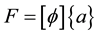 (7)
(7)
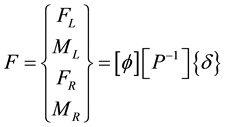 (8)
(8)
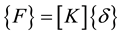 (9)
(9)
Thus, the stiffness matrix [K] is then given by
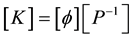 (10)
(10)
The forces at the ends of the element are related to the displacements by the relation
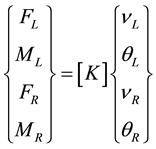 (11)
(11)
Where,
Figure 6. The dynamics of plain beam sub-cell.
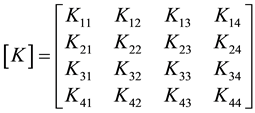 (12)
(12)



When considering a series of cells, one may derive a relation between consecutive left-ends of elements (I to i + 1), Figure 7. It is given by


Where

By substituting the Equation (16) in Equation (13)


Figure 7. Interaction between two consecutive cells.

Then, the transfer matrix, T; may be constructed using the transformation

By substituting the Equations (4-32) in Equations (4- 28)

Or

Thus, the eigenproblem is formulated as

Combining Equations (22) and (23) gives:

The eigenvalues of T occur in pairs





Or


Significant Meaning of the Eigenvalues λ and λ−1 of [T]
Combining Equations (26) and (27) gives:

Indicating that the eigenvalue λ of the matrix [T] is the ratio between the state vectors at two consecutive cells.
Hence, one can reach the following conclusions:
If |λ| = 1, then YK+1 = YK and the state vector propagates along the structure as is. This condition defines a “Pass Band” condition.
If |λ| < 1, then YK+1 < YK and the state vector is attenuated as it propagates along the structure. This condition defines a “Stop Band” condition.
A Further explanation of the physical meaning of the eigenvalue l can be extracted by rewriting it as:

Where m is defined as “Propagation constant” which is a complex number whose real part (α) represents the loga- rithmic decay of the state vector and its imaginary part (β) defines the phase difference between the adjacent cells.
Therefore, the equivalent condition for the pass and stop bands can be written in terms of the propagation constant parameter (α and β) as follows:
1) If α = 0 (et al. m is imaginary), then we have “Pass Band” as there is no amplitude attenuation.
2) If α ≠ 0 (et al. m is real or complex), then we have “Stop Band” as there is amplitude attenuation defined by value of α.
The association of the propagation factor to pass and stop bands can be illustrated in Figure 8.
Figure 9 displays the decay and phase components of the corresponding Propagation Constant µ.
Furthermore, Figure 9(b) demonstrates clearly the “pass and stop bands” are developed. Note that the imaginary part of the propagation constant (µ) which quantifies the phase difference between the wave propagation at adjacent cells is shown to increase gradually from 0 to π. With phase difference between 0 and π, waves will propagate along the periodic structure indicating a “Pass Band”. But, when the phase difference becomes π, destructive interference occurs between adjacent cells and wave propagation along the structure is completely stopped indicating “Stop Band”.
4. Results
To better understand and demonstrate the characteristics
Figure 8. Propagation factor block diagram.


Figure 9. Stop and pass bands of a periodic structure; (a) Real part of propagation constant; (b) Imaginary part of propagation constant.
of periodic structures, a MATLAB program was used for the cell geometry shown in Figure 5, to determine the attenuation characteristics. The materials were selected as Aluminum (a) with E = 70 GPa and ρ = 2700 Kg/m3 and Special Rubber, Mearthane Durethane (b) with E = 0.000345 GPa and ρ = 1150 Kg/m3, the lengths La and Lb were chosen to be 30 mm, 10 mm respectively, where the La, Lb and LC denote the length of the Aluminum material, a length of Rubber material and the length of one cell respectively. Also Da and Db were chosen to be 50 mm and 44 mm respectively, Where the Da and Db denote the diameter of the Aluminum material and Db a diameter of Rubber material in the periodic structure. The propagation parameter for a periodic beam cell obtained is shown in Figure 10, and the magnitude of Frequency Response Function (FRF) shown in Figure 11.
In three cases design and choosing of periodic structure and implementing by MATLAB program as follows: Fixed area Interference (Da/Db) and changing the length of the Cell (Lb/LC), Changing area Interference (Da/Db) either (solid section or hollow section) and fixed length of the Cell (LC) and Changing both the area Interference (Da/Db) between materials and the length of the Cell (Lb/LC).
Figures 12 through 15 show the effect of the changing geometry of the cell, by increasing and decreasing the length lab, on the width and intensity of the stop band of the periodic structure. Fixed Area Interference, (Da/Db) and changing in the length of the cell, (La/Lb). As shown in Table 1.
Figures 16 through 20 show the effect of geometry of the cell, by changing Area Interference (solid section and
Figure 10. Propagation parameter for a periodic beam cell:


hollow section) between materials (Aa/Ab) and fixed the length of cell (La/Lb). As shown in Tables 2-4).
The Figures 21 through 24 indicate that increasing the diameter ratio at the discontinuity (Da/Db) results in improving the attenuation characteristics of the structure particularly over a wide frequency range. Increases the amplitude of decaying factor, increase the no. of stop band and increase the cut-off frequency.
5. FEM
This section exhibit the result of periodic structures with geometrical and material discontinuity by using finite ele- ment method, for a material propertiesshown in Table 5.
5.1. Periodic Structures (Aluminum and Plastic)
The frequency response of periodic structure composed of 3-, 5-, and 7-cells as shown in Figure 23, the periodic beam composed of greater numbers of cell exhibit the attenuation regions more clearly.
5.2. Periodic Structures (Aluminum and Rubber)
This material is very weak and more effective to attenuate the propagation factor over a wide frequency range and has a damping ratio 0.5, It’s clear from Figure 24 the frequency responses almost zero.
6. Conclusions
This dissertation has presented the fundamentals governing the operation of a new class of structures for the legs of offshore platform structure which are exposed to the sea waves. The proposed new class of structures as it was investigated to be periodic in nature; it generated unique dynamic characteristics that make the structures act as
Figure 11. Magnitudes for 1, 3 and 5 cells structures.
mechanical filters for wave propagation. The effect of such unique characteristics of this class of structures in controlling the wave propagation from the sea wave to offshore platform structures was demonstrated theoretically in the spectral domains.
The theoretical equations that govern the operation of
Figure 12. A schematic sketch and stop-pass bands of the periodic structure, (Lb/LCell = 0.08).
Figure 13. Stop-pass bands of the periodic structure, (Lb/LCell = 0.2).
this class of periodic structures are developed using the transfer matrix method. The basic characteristics of the transfer matrices of periodic structures are presented and related to the physics of wave propagation along these structures. The unique filtering characteristics of the periodic structures are demonstrated for various structure configurations. The effect of the design parameter of the structures on their dynamic behavior is investigated for structures with geometrical and material discontinuities at three cases:
Fixed area Interference (Da/Db) and changing length of the Cell (Lb/LC), changing area Interference (Da/Db) ei-
Figure 14. Stop-pass bands of the periodic structure, (Lb/LCell = 0.43).
Figure 15. Stop-pass bands of the periodic structure, (Lb/LCell = 0.54).
Table 1. Fixed area Interference and change the length of cell (LC).
ther (solid section or hollow section) and fixed length ofthecell (LC) change both the area Interference (Da/Db) between materials and length of the Cell (Lb/LC).
The periodic structures have been shown to be an extremely effective means to filter the vibration transmission through the structures. It is found that the passive periodic structures can attenuate the propagation of waves
Figure 16. A schematic sketch and stop-pass bands of the periodic structure, (Da/Db = 0.87).
Figure 17. Stop-pass bands of the periodic structure, (Da/Db = 1.82).
Figure 18. Stop-pass bands of the periodic structure, (Da/Db = 2.5).
Figure 19. A schematic sketch and stop-pass bands of the periodic structure, (Da/Db =1.08).
Figure 20. Stop-pass bands of the periodic structure, (Da/Db = 6.67).
Table 2. Change areas (solid section) and fixed the length of cell (LC).
Table 3. Change areas (hollow section) and fixed the length of ell (LC).
Table 4. Change areas and also change the length of cell (LC).
Figure 21. Propagation factor with frequency response of periodic structure at area contact 151 mm2.
over a broad frequency band extending in most of the considered cases between (0 - 3000) and (0 - 10,000) Hz.
The periodic beams were fabricated at different cells number to provide a better understanding of wave mechanics by using Finite Element Method. As a result in-
Figure 22. Propagation factor with frequency response of periodic structure at area contact 201 mm2.
Figure 23. The frequency response of periodic structure (Aluminum and Plastic) at 3, 5 and 7 cells.
Figure 24. The frequency response of periodic structure (Aluminum and Rubber) at 3, 5 and 7 cells.
Table 5. Material properties.
creasing the destructive interference phenomena by increasing the number of cells, causes more attenuation of waves.
This approach is applicable for wide applications, any system exposed to the vibrations by design and implementing (tailor) the proper solution to provide attenuation phenomenon.
REFERENCES
[1] A. Alghamdi, S. Asiri and A. Mohammed, “Wave Mechanics And Dynamic Response Of The Experimental Model For Offshore Platform With Periodic Legs,” Master Thesis, King Abdulaziz University, Jeddah, 2008.
[2] D. J. Mead, “Free Wave Propagation in Periodically Sup- ported, Infinite Beams,” Journal of Sound and Vibration, Vol. 11, No. 2, 1970, pp. 181-197. http://dx.doi.org/10.1016/S0022-460X(70)80062-1
[3] L. Brillouin, “Wave Propagation in Periodic Structures,” Dover, New York, 1953.
[4] L. Brillouin, “Wave Propagation in Periodic Structures,” 2nd Edition, Dover, New York, 1946.
[5] D. J. Mead, “Vibration Response and Wave Propagation in Periodic Structures,” ASME Journal of Engineering for Industry, Vol. 93, No. 3, 1971, pp. 783-792. http://dx.doi.org/10.1115/1.3428014
[6] D. J. Mead, “Wave Propagation and Natural Modes in Periodic Systems: I. Mono-Coupled Systems,” Journal of Sound and Vibration, Vol. 40, No. 1, 1975, pp. 1-18. http://dx.doi.org/10.1016/S0022-460X(75)80227-6
[7] D. J. Mead and S. Markus, “Coupled Flexural-Longitudi- nal Wave Motion in a Periodic Beam,” Journal of Sound and Vibration, Vol. 90, No. 1, 1983, pp. 1-24. http://dx.doi.org/10.1016/0022-460X(83)90399-1
[8] D. J. Mead, “Loss Factors and Resonant Frequencies of Periodic Damped Sandwiched Plates,” ASME Journal of Engineering for Industry, Vol. 98, No. 1, 1976, pp. 75-80. http://dx.doi.org/10.1115/1.3438877
[9] D. J. Mead, “A New Method of Analyzing Wave Propagation in Periodic Structures; Applications to Periodic Ti- moshenko Beams and Stiffened Plates,” Journal of Sound and Vibration, Vol. 104, No. 1, 1986, pp. 9-27. http://dx.doi.org/10.1016/S0022-460X(86)80128-6
[10] D. J. Mead, “Wave Propagation in Continuous Periodic Structures: Research Contributions from Southampton,” Journal of Sound and Vibration, Vol. 190, No. 3, 1996, pp. 495-524. http://dx.doi.org/10.1006/jsvi.1996.0076
[11] D. J. Mead and N. S. Bardell, “Free Vibration of a Thin Cylindrical Shell with Periodic Circumferential Stiffeners,” Journal of Sound and Vibration, Vol. 115, No. 3, 1987, pp. 499-521. http://dx.doi.org/10.1016/0022-460X(87)90293-8
[12] C. H. Hodges, “Confinement of Vibration by Structural Irregularity,” Journal of Sound and Vibration, Vol. 82, No. 3, 1982, pp. 441-444. http://dx.doi.org/10.1016/S0022-460X(82)80022-9
[13] C. H. Hodges and J. Woodhouse, “Vibration Isolation from Irregularity in a Nearly Periodic Structure: Theory and Measurements,” Journal of the Acoustical Society of America, Vol. 74, 1983, pp. 894-905. http://dx.doi.org/10.1121/1.389847
[14] J. F. Doyle, “Wave Propagation in Structures,” Springer, New York, 1997. http://dx.doi.org/10.1007/978-1-4612-1832-6
[15] L. Cremer, M. Heckel and E. Ungar, “Structure-Borne Sound,” Springer-Verlag, New York, 1973. http://dx.doi.org/10.1007/978-3-662-10118-6
[16] G. Gupta, “Natural Flexural Waves and the Normal Mo- des of Periodically-Supported Beams and Plates,” Journal of Sound and Vibration, Vol. 13, No. 1, 1970, pp. 89-111. http://dx.doi.org/10.1016/S0022-460X(70)80082-7
[17] M. Faulkner and D. Hong, “Free Vibrations of a Mono- Coupled Periodic System,” Journal of Sound and Vibration, Vol. 99, No. 1, 1985, pp. 29-42. http://dx.doi.org/10.1016/0022-460X(85)90443-2
[18] D. J. Mead and Y. Yaman, “The Harmonic Response of Rectangular Sandwich Plates with Multiple Stiffening: A Flexural Wave Analysis,” Journal of Sound and Vibration, Vol. 145, No. 3, 1991, pp. 409-428. http://dx.doi.org/10.1016/0022-460X(91)90111-V
[19] D. J. Mead, R. White and X. M. Zhang, “Power Transmission in a Periodically Supported Infinite Beam Excited at a Single Point,” Journal of Sound and Vibration, Vol. 169, No. 4, 1994, pp. 558-561. http://dx.doi.org/10.1006/jsvi.1994.1539
[20] G. J. Kissel, “Localization Factor for Multichannel Disordered Systems,” Physical Review A, Vol. 44, No. 2, 1991, pp. 1008-1014. http://dx.doi.org/10.1103/PhysRevA.44.1008
[21] M. Ruzzene and A. Baz, “Attenuation and Localization of Wave Propagation in Periodic Rods Using Shape Memoryinserts,” Unpublished, 2000.
[22] M. Ruzzene and A. Baz, “Control of Wave Propagation in Periodic Composite Rods Using Shape Memory Inserts,” Journal of Vibration and Acoustics, Vol. 122, 2000, pp. 151-159.
[23] S. Asiri, A. Baz and D. Pines, “Active Periodic Struts for a Gearbox Support System,” Smart Materials Structures, Vol. 15, No. 6, 2006, pp. 1707-1714.
[24] S. Asiri, “Vibration Attenuation of Automotive Vehicle Engine Using Periodic Mounts,” International Journal of Vehicle Noise and Vibration, Vol. 3, No. 3, 2007, pp. 302-315.
[25] S. Asiri, M. Adbussalam and A. Alghamdi, “Dynamic Response of an Experimental Model for Offshore Platforms with Periodic Legs,” Journal of King Abdulaziz University Engineering Sciences, Vol. 20, No. 1, 2009, pp. 93-121.
































