World Journal of Mechanics
Vol. 3 No. 6 (2013) , Article ID: 36191 , 5 pages DOI:10.4236/wjm.2013.36027
Linear, Cubic and Quintic Coordinate-Dependent Forces and Kinematic Characteristics of a Spring-Mass System
University College, Pennsylvania State University, York, USA
Email: has2@psu.edu
Copyright © 2013 Haiduke Sarafian. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 4, 2013; revised July 6, 2013; accepted August 1, 2013
Keywords: Linear; Cubic and Quintic Nonlinear Oscillations; Semi-Analytic Solution to Equation of Motion; Mathematica
ABSTRACT
By combining a pair of linear springs we devise a nonlinear vibrator. For a one dimensional scenario the nonlinear force is composed of a polynomial of odd powers of position-dependent variable greater than or equal three. For a chosen initial condition without compromising the generality of the problem we analyze the problem considering only the leading cubic term. We solve the equation of motion analytically leading to The Jacobi Elliptic Function. To avoid the complexity of the latter, we propose a practical, intuitive-based and easy to use alternative semi-analytic method producing the same result. We demonstrate that our method is intuitive and practical vs. the plug-in Jacobi function. According to the proposed procedure, higher order terms such as quintic and beyond easily may be included in the analysis. We also extend the application of our method considering a system of a three-linear spring. Mathematica [1] is being used throughout the investigation and proven to be an indispensable computational tool.
1. Motivation and Objectives
Literature articles and text books are flooded with sections describing the characteristics of linear oscillators [2]. One quick review of these resources reveals these are confined limited to mechanical systems. In the area of electro and magneto-dynamics, the author thoroughly has investigated scenarios of nonlinear oscillators [3,4]. Laboratory setups conducive to these scenarios have been proposed, and for the magneto-dynamic case the validity of the theoretical model is qualified with actual data [5]. For the sake of completeness, therefore, it is essential to fill in the gap considering a practical scenario conducive to a nonlinear mechanical oscillator. Although the latter is the main motivation of tackling the issue, however, in the course of analyzing the problem we stumbled on a mathematical observation constituting our secondary objective.
To address the first issue we consider combining two linear springs; the device is shown in Figure 1. The springs are identical in shape and have the same stiffness. They are fastened to two separate supports at one end and jointly hold a marble at the other end. In the absence of gravity, the springs exert a nonlinear force on the marble along the horizontal direction when it is pulled away symmetrically from equilibrium. The non-linear force could be a combination of cubic and quintic coordinate-dependent terms; details are discussed in the next section.
Releasing the marble somewhere off from equilibrium results in oscillations along the horizontal direction. The corresponding equation of motion is a nonlinear differential equation. The issues concerning the solution of the equation will be discussed later. Nonetheless, it is worthwhile mentioning not only we solve the equation utiliz-

Figure 1. Two-spring arrangement leading to cubic and quintic oscillations.
ing traditional methods, we propose a fresh semi-analytic method resulting in the same output. With these objectives we craft this four-section article. In addition to Motivation and Objectives, in Section 2, along with the physics of the problem we formulate the problem. In Section 3 we present the Analysis along with the associated descriptive graphs. We close the article with conclusions and closing remarks.
2. Physics of the Problem and Its Formulation
As shown in Figure 1, the marble is pulled from its initial equilibrium position to a point such as G, stretching the linear springs with stiffness k beyond their relaxed length L. The differential length elongation of each spring is , yielding the net force
, yielding the net force
 (1)
(1)
For displacement x < L the quantity in the parentheses in Equation (1) may be replaced with

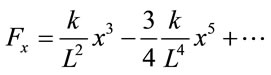 (2)
(2)
One realizes this simple mechanical device is capable of exerting nonlinear forces; the forces are a combination of cubic and quintic coordinate-dependent terms. For the sake of “completeness”, in order to include a linear coordinate-dependent force we modify the previous design by adding a third identical spring, shown in Figure 2.
For this three-spring system the net force is,
 (3)
(3)
The criteria x < L suggests that the impact of the third term and terms with powers higher than the fifth are to be insignificant; this is qualified later on. Nonetheless, the equation of motion of the marble under the influence of the force given by Equation (3) along the x-axis yields,
 (4)
(4)
with this equation in hand we analyze the impact of the force terms on the kinematic characteristics of the mobile marble. First, by turning off the linear term, a scenario subject to Figure 1, we focus on the impact of the cubic and quintic terms. Then, we consider a case including the combination of the linear and the cubic terms.
3. Analysis
3.1. Case 1
According to the scenario shown in Figure 1 and its ac-

Figure 2. Three-spring arrangement leading to a combination of linear, cubic and quintic oscillations.
companied force, Equation (2), the equation of motion is,
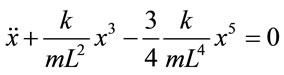 . (5)
. (5)
First we consider a case assuming x < L, i.e. the initial displacement of the marble from equilibrium is less than the length of the spring; this drops the last term. Sustaining the cubic term only, the equation of motion is an analytically solvable DE with closed form solutions given by Jacobi Elliptic Functions [6]. Alternatively, the same equation can be solved numerically. Assigning parameters to the spring length and stiffness and the marble we solve the equation numerically; output graphs of these two approaches are indistinguishable. To establish the basis for the semi-analytic method we focus on the numeric schematic. The values lists a typical set of parameters in MKS units,
 .
.
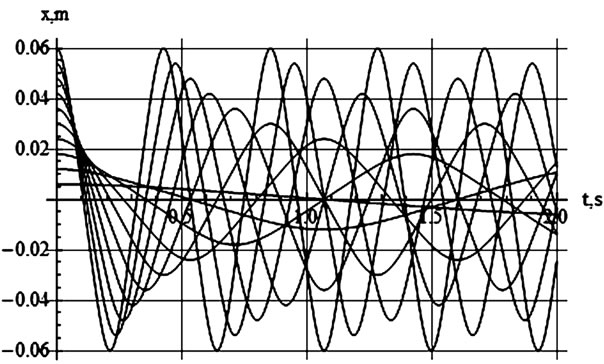
The 4 × 2 graphic-matrix shown in Figure 3 displays the position of the marble vs. time. The differences between the graphs are due only to various initial displacements of the marble. From the top left to the bottom right these correspond to  respectively. The common global feature of these plots indicate irrespective of the initial condition the marble under the influence of the cubic force does oscillate. The period of oscillation is not constant; it depends on the initial value of the displacement. This is one the distinct characteristics of a nonlinear force. An inspection of these plots reveals the absence of retarding forces such as friction enforces the constant amplitude; noting the shorter the amplitude the longer the period. Figure 4 puts the observation in perspective. This graph vividly shows a reciprocal relationship between the amplitude and the corresponding period.
respectively. The common global feature of these plots indicate irrespective of the initial condition the marble under the influence of the cubic force does oscillate. The period of oscillation is not constant; it depends on the initial value of the displacement. This is one the distinct characteristics of a nonlinear force. An inspection of these plots reveals the absence of retarding forces such as friction enforces the constant amplitude; noting the shorter the amplitude the longer the period. Figure 4 puts the observation in perspective. This graph vividly shows a reciprocal relationship between the amplitude and the corresponding period.
It is instructive to compare the oscillations emanating by a cubic force vs. the linear one. This can be done ei-

Figure 3. Output of numeric solution of equation of motion. From the top left to the bottom right the graphs correspond to the initial values x[0] = 0.1 α l for α = 1, 2, 3, ..., 8, respectively.
ther by a direct comparison of the amplitudes or more elegantly by comparing their respective phase diagrams shown in Figure 5.
For the sake of clarity the horizontal scale of Figure 5 is magnified by a factor of 10. Figure 5 shows the distinct differences between the oscillation characteristics of a linear vs. a cubic spring. As one may easily prove the phase diagram of a linear spring is a perfect ellipse. The phase diagram of a cubic spring is a depressed “ellipse” along the velocity axis. Depression severity of the latter is a function of the initial condition. A family of such curves is shown in Figure 6.
Figure 6 displays a series of phase diagrams each of which is a result of applying various initial conditions. For instance the inner depressed ellipse comes about from setting the initial displacement to  whereas the outer one is associated with the initial displacement
whereas the outer one is associated with the initial displacement . The curves between the inner and the outer ellipses correspond to initial displacements
. The curves between the inner and the outer ellipses correspond to initial displacements  α for α = 2, 3, 4, ..., 9, respectively.
α for α = 2, 3, 4, ..., 9, respectively.
3.2. Semi-Analytic Method of Solving DE Motion
As we discussed in Section 3.1 the solution of equation of motion of a cubic force is an oscillating function.
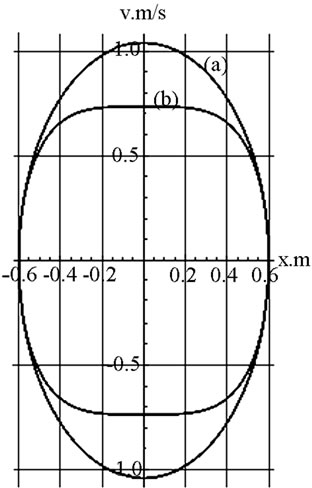
Figure 5. Phase diagrams: (a) the ellipse corresponds to a linear spring, and (b) the depressed ellipse corresponds to a cubic spring.
Accordingly, the value of the initial condition impacts the period. With these two observations we propose a compatible alternative solution. This solution is neither purely numeric nor purely symbolic; it is somewhere in between, it is semi-analytic. From an analytic point of view, first we consider a solution such as, 
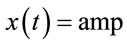 , with ω = ω(amp). Because
, with ω = ω(amp). Because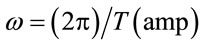 , from a numeric point of view utilizing either Figure 4 or 5 we hunt for T(amp). For instance, for the latter utilizing Figure 5 for the chosen initial amplitude we evaluate the maximum ordinate of the corresponding oscillation. A set of one such coordinates are shown with dots in Figure 7. Then we fit the data with an appropriate continuous function. The fitted curve is shown on the same graph as well. Utilizing this function, e.g. T(amp) we compare the semi-analytic solution
, from a numeric point of view utilizing either Figure 4 or 5 we hunt for T(amp). For instance, for the latter utilizing Figure 5 for the chosen initial amplitude we evaluate the maximum ordinate of the corresponding oscillation. A set of one such coordinates are shown with dots in Figure 7. Then we fit the data with an appropriate continuous function. The fitted curve is shown on the same graph as well. Utilizing this function, e.g. T(amp) we compare the semi-analytic solution 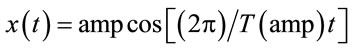 vs. the numeric solution. A 4 × 2 graphic-matrix shown in Figure 8, qualifies the accuracy of our proposed method.
vs. the numeric solution. A 4 × 2 graphic-matrix shown in Figure 8, qualifies the accuracy of our proposed method.
These two solutions are indistinguishable. Therefore,
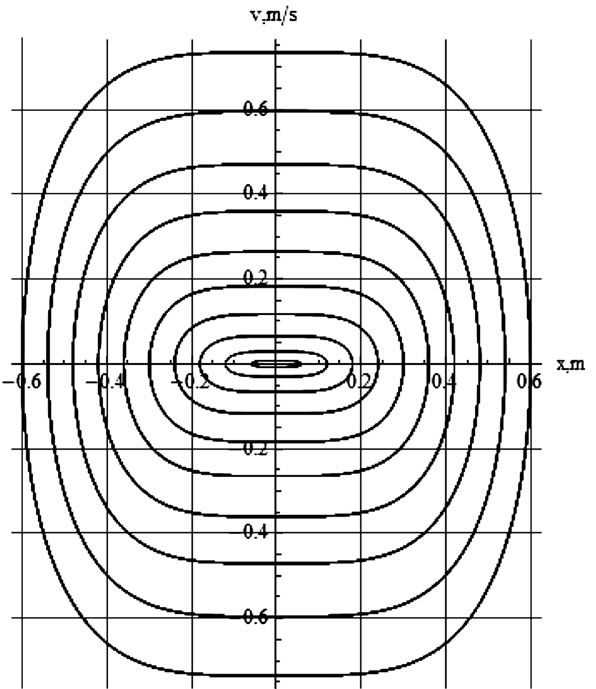
Figure 6. A family of phase diagrams of the cubic spring. The inner curve corresponds to x[0] = 0.1 while the outer one is due x[0] = 1.
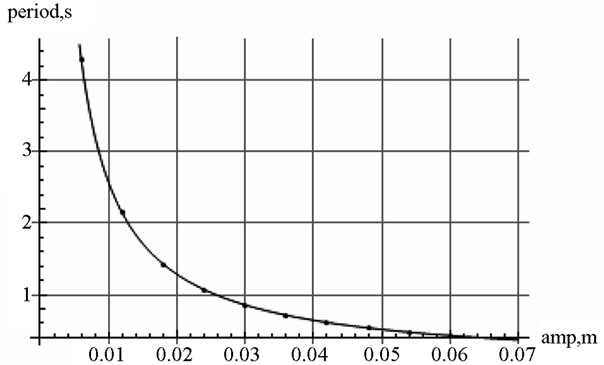
Figure 7. The dots are the periods and the corresponding amplitudes are deduced from Figure 5. The solid line is the fitted curve T(amp) = 0.0256907 amp−1.
as an option, rather than utilizing the numeric solution that in general lacks the physics insight, alternatively, one may objectively apply the semi-analytic method to obtaining the same result.
3.3. Case 2
In this section we present the results pertaining scenario shown in Figure 2. The equation of motion is,
 (6)
(6)
Equation (6) has an analytic closed solution; these are Jacobi Elliptic Functions [6,7]. These functions compar-

Figure 8. Comparison of the numeric solutions (black curves) vs. semi-analytic solution (gray curves) shown in Figure 2.

Figure 9. The dots are the periods and their corresponding amplitudes are deduced from oscillations subject to Equation (6). The solid line is the fitted curve T(amp) = 0.3649 − 6.8834 amp1.5327.
ing to their counterparts of Case 1 have more complex arguments. This may be the trust of adapting the semi-analytic method for solving this equation. Following the procedure outlined in Section 3.1, Figure 9 displays the evaluated data, i.e. periods vs. amplitudes and the fitted curve. Utilizing the fitted function, e.g. T(amp) we compare the semi-analytic solution  vs. the numeric solution. The 4 × 2 graphi matrix shown in Figure 10 again qualifies the equivalency of the pro-
vs. the numeric solution. The 4 × 2 graphi matrix shown in Figure 10 again qualifies the equivalency of the pro-
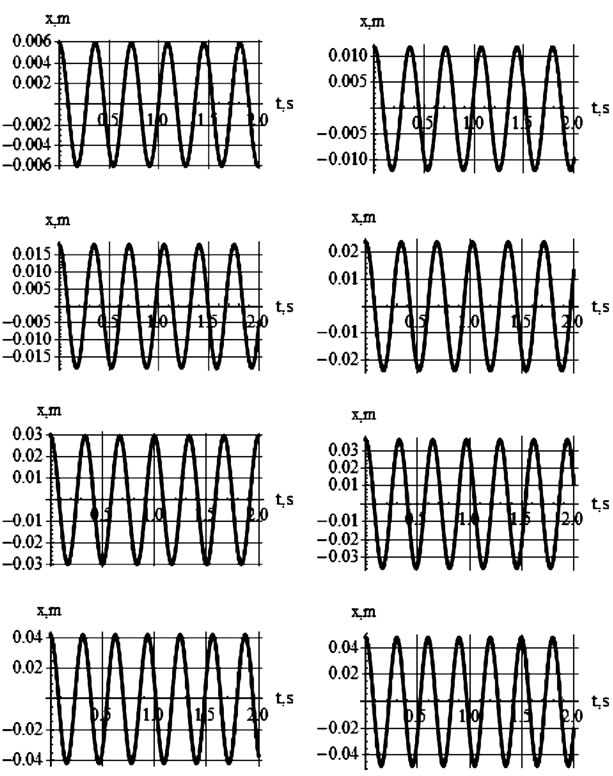
Figure 10. Comparison of the numeric solutions (black curves) vs. semi-analytic solution (gray curves).
posed method.
As in Case 1, solutions are indistinguishable.
4. Conclusions and Remarks
The objective of this study is to design a mechanical system capable of oscillating under the influence of nonlinear forces. Utilizing a set of two and three linear springs we design two such devices; many more may be devised. These are complementary to our previous studies completing the scope of nonlinear oscillations in three different areas of physics: mechanics, electrodynamics and magnetodynamics. Beyond discussing the physics of the problem, we introduce a semi-analytic method to objectively obtain analytic solutions for the equations of motion. From mathematics point of view the proposed method for solving DE relies on numeric solution of DE. The output of the semi-analytic method is an analytic function embodying the desired objective properties. To distinguish the differences between the linear vs. nonlinear oscillations their phase diagrams are compared. However, for a visual understanding (not included here), the author utilizing Mathematica has simulated the motion. Watching the movement of the marble under the influence of nonlinear forces gives a valuable experience. Alternatively, one may simulate (as the author has done) the motion utilizing Cinderella. The latter is less objective and bypasses the need for numeric input.
REFERENCES
- Mathematica, “A General Computer Software System and Language Intended for Mathematical and Other Applications,” V9.0, Wolfram Research, 2013.
- Tronton and Marion, “Classical Dynamics of Particles and Systems,” 5th Edition, Cengage Learning, 2008.
- H. Sarafian, “Static Electric-Spring and Nonlinear Oscillations,” Journal of Electromagnetic Analysis & Applications, Vol. 2, No. 2, 2010, pp. 75-81.
- H. Sarafian, “Nonlinear Oscillations of a Magneto Static Spring-Mass,” Journal of Electromagnetic Analysis and Applications, Vol. 3, No. 5, 2011, pp. 133-139. doi:10.4236/jemaa.2011.35022
- H. Sarafian, “Dynamic Dipole-Dipole Magnetic Interaction and Damped Nonlinear Oscillations,” Journal of Electromagnetic Analysis & Applications, Vol. 1, No. 4, 2009, pp. 195-204. doi:10.4236/jemaa.2009.14030
- Jacobi Elliptic Functions. http://mathworld.wolfram.com/JacobiEllipticFunctions.html
- J. Richter-Gebert and U. H. Kortenkamp, “The Interactive Geometry Software,” Cinderella 2.0, Springer, 2012.