World Journal of Mechanics
Vol.3 No.2(2013), Article ID:30856,12 pages DOI:10.4236/wjm.2013.32007
Pitting Corrosion Investigation of Cantilever Beams Using F. E. Method
Faculty of Aerospace Engineering, Technion, Haifa, Israel
Email: syanki@tx.technion.ac.il
Copyright © 2013 Jacob Nagler. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 2, 2012; revised March 18, 2013; accepted March 25, 2013
Keywords: Pitting Corrosion; Carbon Steel; Bernoulli Euler; Simulation
ABSTRACT
Carbon steel cantilever beams are widely used in many applications in aerospace, civil and mechanical engineering. Pitting corrosion is a phenomenon which places severe limitations on the design of such applications. As such, understanding this phenomenon and the methods to deal with it, are of a great importance. This paper presents numerical investigation by using F. E. (Finite Element) simulation on the load carrying capacity of corroded cantilever beams with pitting corrosion damage. The pitting corrosion hole shape has been modeled using ASTM G46 Standard Guide. Several different cases of pitting corrosion, represented by hemispherical holes, were modeled and examined by using ANSYS computer program. Clamped edge constraint was used on one end, while the other end was free. In these F. E. models, element of Solid95 was used and comparison to Bernoulli-Euler theory was made. The effect of the radius of the pitting corrosion holes on the stresses in the beam was examined in comparison to yield stress. It has been found that the M. S. (Margin of Safety) has been reduced gradually with increasing radii. Agreement with Bernoulli-Euler theory has been achieved only for small radii. Moreover, three methods of pitting corrosion repairs were examined, together with Bernoulli-Euler theory comparison: 1) Regular surface repair; 2) Extension surface repair; and 3) “Handy Removal”. It was found that extension surface repair has the highest M. S. value.
1. Introduction
Pitting corrosion is a critical problem in many fields such as civil engineering, ocean engineering and aircraft integrity design. In some cases, it can cause the formation of fatigue cracks, increase in the internal stresses and strength reduction. Pitting corrosion phenomenon, including other types of corrosion, has been investigated experimentally by Hoeppner [1] and Zhang et al. [2]. The fatigue of pre-corroded aluminum plate was investigated experimentally by Piprani et al. [3].
In addition, F. E. simulations and numerical calculations have been made on the subject for different geometries of mechanical components. For instance, Chatterjee et al. [4] investigated pitting corrosion effect on cantilever beam in case of breathing crack under harmonic loading by using modal analysis. Also, model of one side pitted steel plates under uniaxial compression has been examined by Nouri et al. [5]. In addition, analysis of the mechanical properties of corroded deformed steel bar was prepared by Gang et al. [6].
Additionally, studies that include both experimental and numerical simulations were conducted by Potisuk et al. [7] and Zhang et al. [8] on reinforced concrete beams with corrosion subjected to shear and on micro-sized 304 stainless steel beams respectively.
A thorough investigation that included F. E. analysis together with experimental data was done by Ruwan [9]. The latter study deals with reduction of ultimate strength due to corrosion and concentrates on experimental data tests.
In contrary to many of the recent studies, this article concentrates on F. E. analysis rather than experimental data. In addition, a comparison to Bernoulli-Euler theory with the presence of pitting corrosion is performed. The last part of this article suggests three repair methods of pitting corrosion damage and comparison to Bernoulli-Euler theory is included.
In this study, a simulation of corroded cantilever beam has been done by using F. E. analysis and compared to Bernoulli-Euler theory. The pitting corrosion hole has been modeled by using hemispherical shape. The influence of hemispherical corrosion radius has investigated and comparison to Bernoulli-Euler theory was made. Eventually, three methods for repair of corrosion damage have been proposed and examined by using F. E. method and compared to Bernoulli-Euler theory.
2. Model Geometry
The Beam in Figure 1 is full section-profile. The geometry of the pit hole is modeled by hemispherical hole that is presented in Figure 1. The assumption of using hemispherical hole shape in order to model corrosion is derived from ASTM G46 Standard Guide [10] for the “Examination and Evaluation of Pitting Corrosion”.
The width and height of the section are represented by the parameters (b, h) and P is the force that is applied on the right end of the cantilever beam area. The left end of the cantilever beam is fully constrained and L represents the cantilever span. These geometric parameters are summarized in Table 1.
3. General Finite Element Model
The F. E. M. model has been created by using ANSYS 10.0 program. The model includes geometry, mechanical properties of the carbon steel and appropriate mesh selection and refinement.
The elements that were used to create the basic model are Solid95. According to ANSYS 10.0 information documents [12] these elements are higher order version of the 3-D 8-node solid element. It can tolerate irregular shapes without as much loss of accuracy. SOLID95 elements have compatible displacement shapes and are well suited
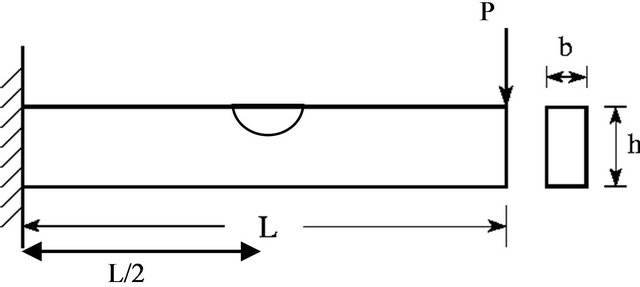

Figure 1. Pitting corrosion analytic model.
to model curved boundaries. The element is defined by 20 nodes having three degrees of freedom per node: translations in the nodal x, y, and z directions. The element may have any spatial orientation. SOLID95 has plasticity, creep, stress stiffening, large deflection, and large strain capabilities.
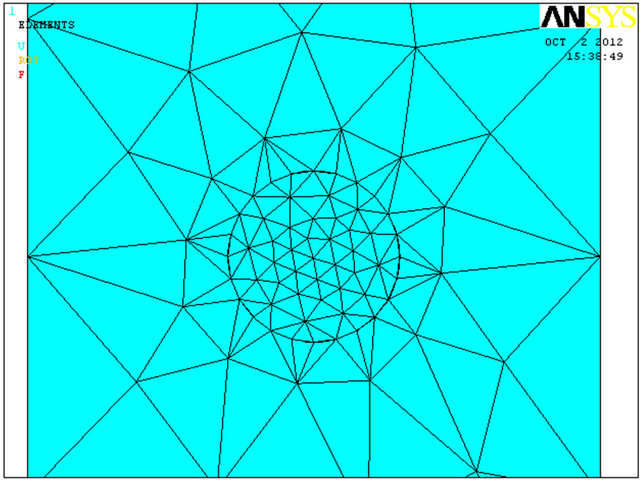
The mesh refinement must satisfy the need for a fine mesh to give an accurate stress distribution in a reasonable analysis time. The optimal solution is to use a finer mesh in areas of high stress: in the hemi spherical hole of the pitting corrosion and in the supports regions, respectively (Figure 2).
Total load of 73575N was applied on 9 nodes connected to area in the right end of the beam. Also, the left end surface area is restrained in every possible direction.
The material model that was used is AISI 1025 carbon steel. The yield and ultimate tensile stresses considered for the beam according to MIL-HDBK-5H [11] were 248- MPa and 379 MPa respectively. The steel was modeled for Young’s modulus E equals to 2 × 105 and Poisson’s ratio ![]() equals to 0.32. Geometrical and material model parameters are summarized in Table 1.
equals to 0.32. Geometrical and material model parameters are summarized in Table 1.
Additionally, three different repair methods were established and modeled by F. E. M. The first repair method as illustrated in Figure 3 simulates surface of 1 mm thickness that covers only the upper area of the hemi-sphere surface. The elements that were used to create repair area are SOLID95. The reason for using SOLID95 instead of Shell elements is due to the bending of the cantilever beam that creates out of plane stresses and movement deflection that cannot be considered in shell structure. Comparison to shell elements repair is presented in this paper and discussed in Section 5.
Shell elements model for the first repair is illustrated in Figure 4. The elements that were used in this repair method are SHELL 181. According to [12] these elements are well suited to model thin to moderately-thick shell structures. It is a 4-node element with six degrees of freedom at each node: translations in the x, y, and z di
Table 1. Geometrical and material model parameters.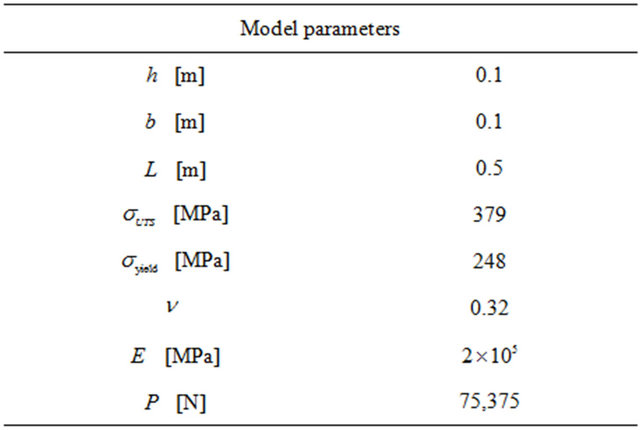
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 2. (a)-(d) Mesh discretization of the corrosion model.
rections, and rotations about the x, y, and z-axes. SHELL- 181 is well-suited for linear, large rotation, and/or large strain nonlinear applications. Change in shell thickness is accounted for in nonlinear analyses.
The second repair is an extension of the first repair by creating thick layer plate (0.06 × 0.06 × 0.01) that covers not only the hole but also the regions around it. The model was built by SOLID95 elements as illustrates in Figure 5. The reason for using SOLID95 elements instead of SHELL elements is the same as for the first repair method.
The third repair method is called “Handy Removal” and is based on removing the corrosion by mechanical means. The removal geometrical model situation is shown in Figure 6.
Comparison between the repairs above and the influence of pitting corrosion on material strength will be discussed in Section 5.
The Bernoulli Euler equations of deflection and bending stress respectively are given by:
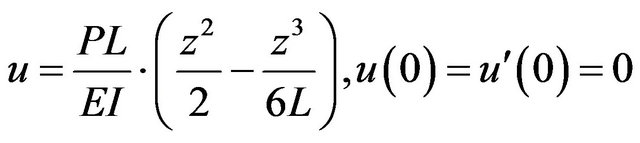 (1)
(1)
while ![]() is the deformation as function of
is the deformation as function of  axis and
axis and  is the second moment of inertia.
is the second moment of inertia.
 (2)
(2)
while  is the bending moment and
is the bending moment and ![]() is the maximum perpendicular distance to the neutral axis that in our case is
is the maximum perpendicular distance to the neutral axis that in our case is  .
.
Substitution of 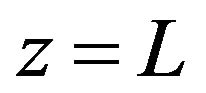 and
and  in Relations (1)-(2)
in Relations (1)-(2)
while 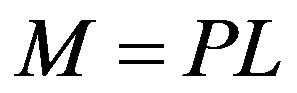 leads to:
leads to:
 (3)
(3)
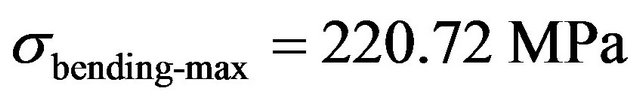 (4)
(4)
Comparison between Bernoulli-Euler theory (Equations (3) and (4)) and pitting corrosion F. E. model for the stress and deflection will be will be made in the next sections.
4. Model Calibration
In order to make credible comparison to Bernoulli-Euler theory, model calibration should be made. The F. E. model calibration is made of SOLID95 elements and no
 (a)
(a)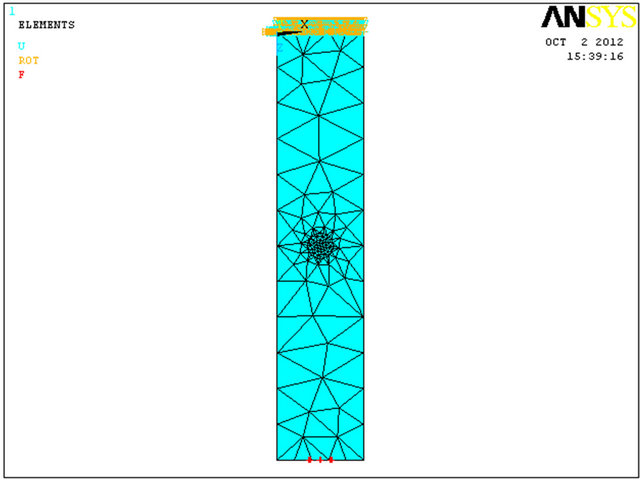 (b)
(b)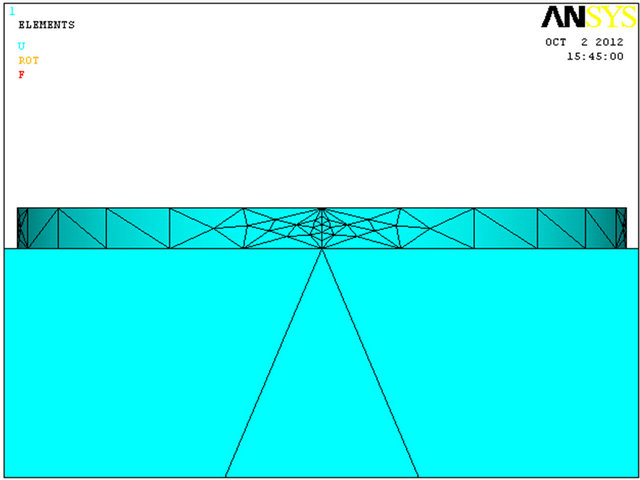 (c)
(c)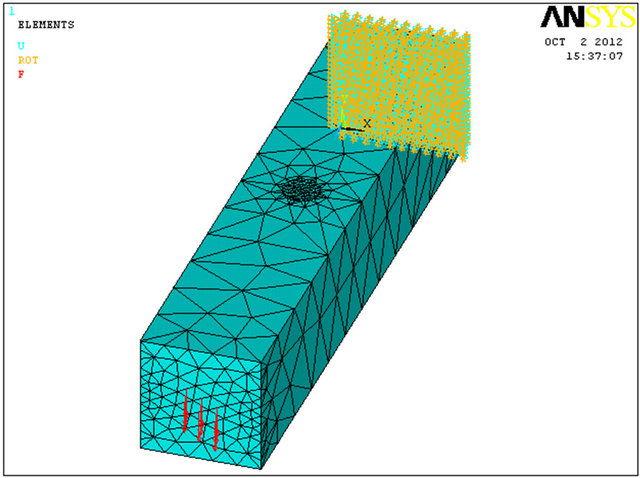 (d)
(d)
Figure 3. (a)-(d) Mesh discretization of the first repair model by solid elements.
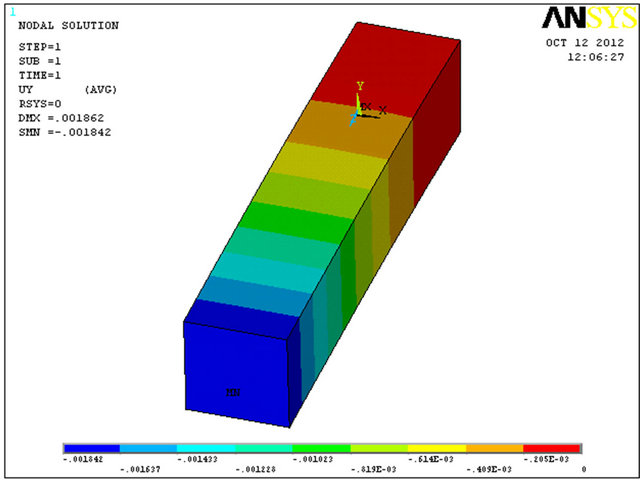
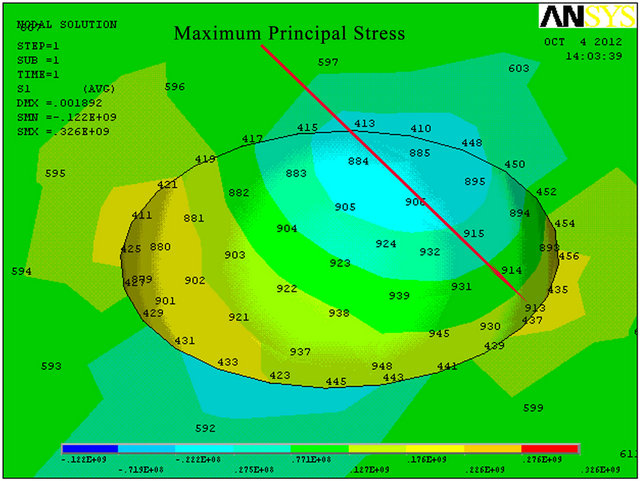
corrosion pitting is modeled. The model is bounded in one end and the other end is subjected to a bending force on its area. The displacement in axis Y direction (see Figure 7) and principal stress simulates deflection and bending stress, respectively.
F. E. model together with maximum deflection and principal stress results are presented in Figure 7. It seems that the error is negligible for principal stress (2%) and for the maximum deflection it is zero (“0”% error—the numerical calculation has its own accurate limit). As a result, the model calibration assumption is valid.
5. Results
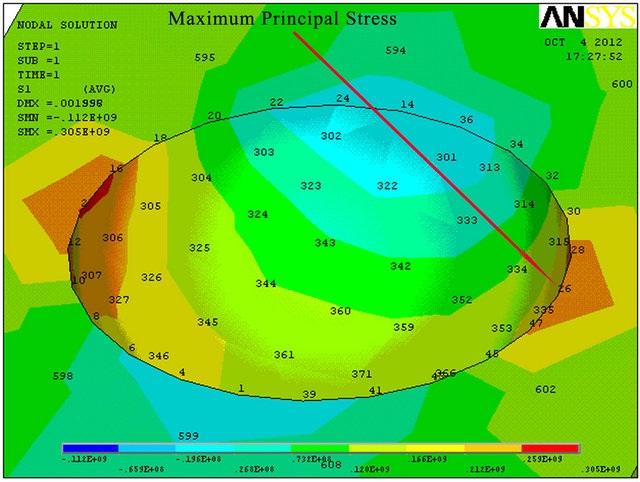
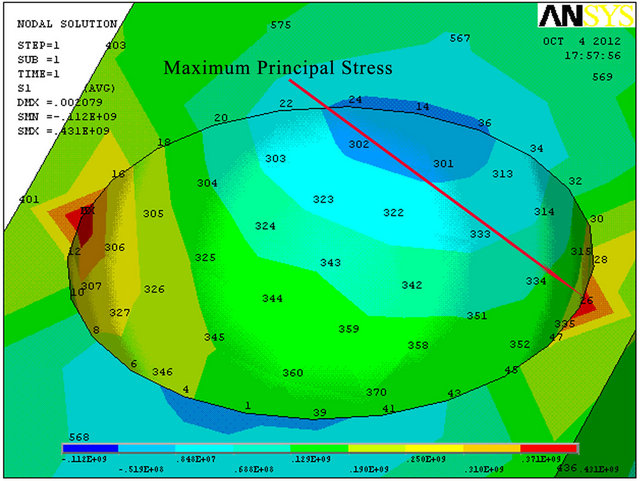
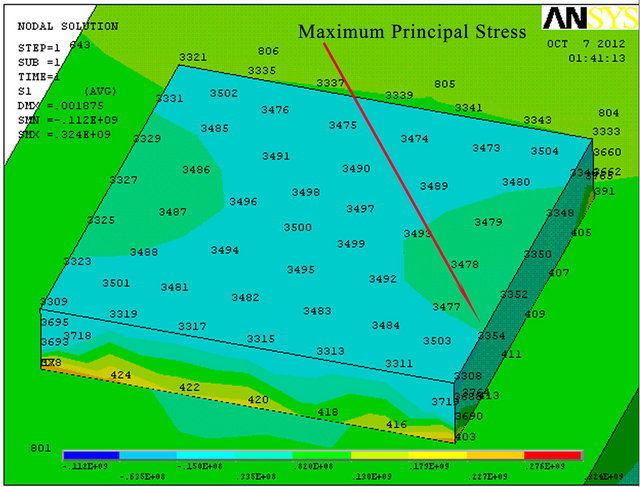
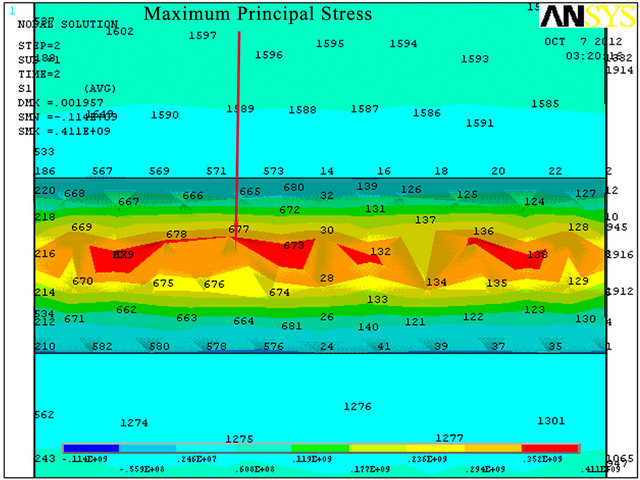
The influence of the corrosion pitting on the beam’s strength has been examined by F. E. analysis. Three ratios of pitting corrosion hemisphere were modeled independently. It was found that the maximum principal stress is obtained on the circular shape of the corrosion according to Figures (8)-(10). Corrosion diameter sizeincreasing leads to M. S. (margin of safety) decreasing and deflection increasing (see Table 2). The reason for that is due to cross section reduction that leads to stress concentration.
In addition, agreement with Bernoulli-Euler theory and pitted corrosion beam F. E. model as shown in Table 3 was found only in cases where the diameter of the pitting corrosion was small enough (about 0.32%, 15% and 47% error for 30 mm, 60 mm and 80 mm, respectively). One possible explanation for this phenomenon can be understood by saying that Bernoulli assumption (“cross-sectional planes during bending deformation remain planes and perpendicular to the neutral axis”) is no longer necessary valid for increasing diameter size of hemi-spherical hole corrosion.
Comparison between shell and solid elements in case of 30 mm diameter shows that solid elements are more accurate in cases where the thickness is more critical and out of plane stresses and deflection play a main role as shown in Figure 11.
The sensitivity of the corrosion pitting repair has also been examined by F. E. analysis. Three kinds of pitting co-
 (a)
(a)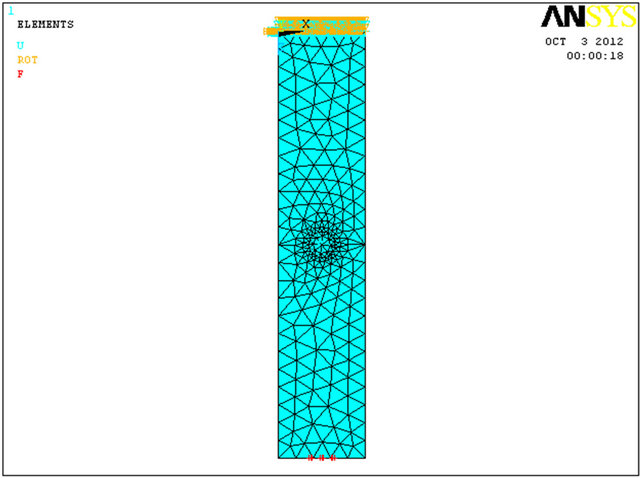 (b)
(b) (c)
(c)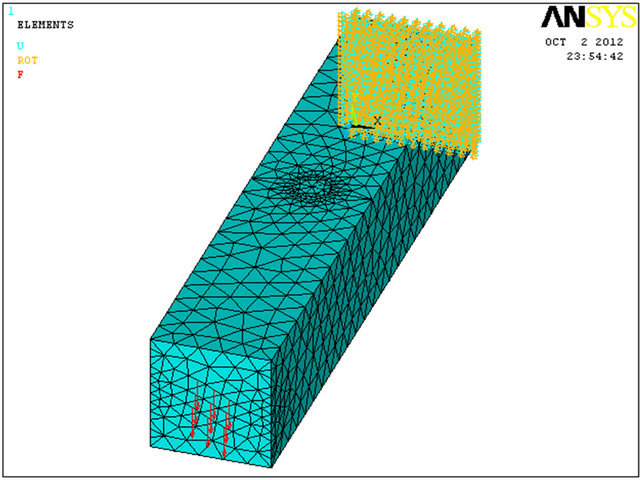 (d)
(d)
Figure 4. (a)-(d) Mesh discretization of the first repair model by shell elements.
Table 2. Cantilever beam with pitted corrosion results.
rrosion repair were modeled independently. The diameter that was chosen to be repaired was 30 mm. Results of the three models are shown in Figures (12)-(14).
Comparisons between these repairs for principal stress, deflection and M. S. parameters are summarized in Table 4.
The surface extension repair method was found to be with maximal M. S. value while handy removals repair method was found to be with minimal M. S. value. The handy removal repair method is based on cross section
Table 3. Bernoulli-Euler vs Cantilever beam with pitted corrosion results.
reduction that causes to highly stress concentration value and therefore it’s the least effective method to use.
In addition, agreement with Bernoulli-Euler theory for these repairs as shown in Table 5. was found only for extension surface repair (3.8% error) but for regular surface and handy removal repairs it was found to be inadequate (about 27% and 40% error respectively). Possible explanation for this phenomenon is laid on repair surface effectiveness; by connecting to as many nodes as possible, the repair surface area is large enough to cause
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 5. (a)-(d) Mesh discretization of the second repair model—“Extension Repair”.
 (a)
(a) (b)
(b)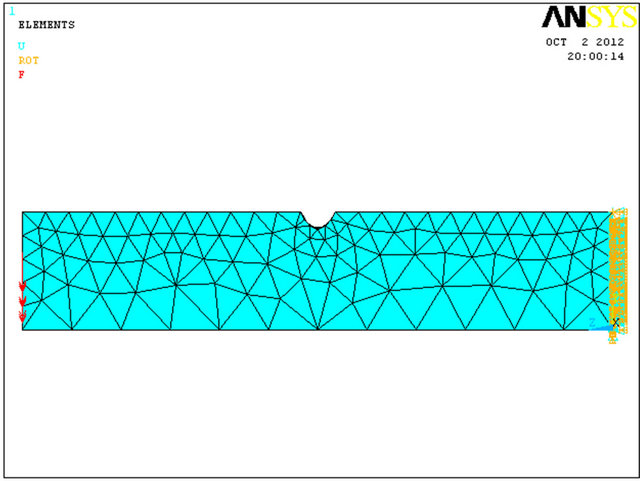 (c)
(c)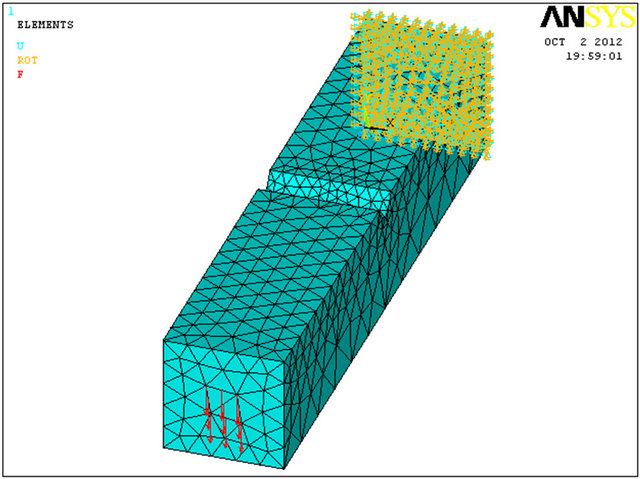 (d)
(d)
Figure 6. (a)-(d) Mesh discretization of the third repair model—“Handy Removal Repair”.
 (a)
(a) (b)
(b)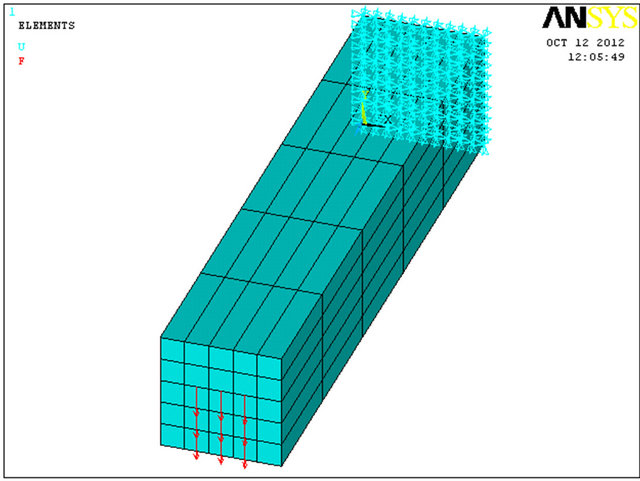 (c)
(c)
Figure 7. (a)-(c) Model calibration.
 (a)
(a) (b)
(b)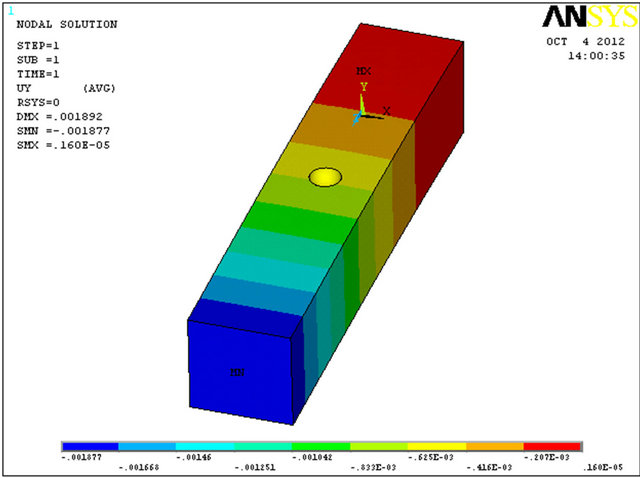 (c)
(c)
Figure 8. (a)-(c) Principal stress and deflection results of 30 mm pitting corrosion diameter.
 (a)
(a) (b)
(b) (c)
(c)
Figure 9. (a)-(c) Principal stress and deflection results of 60 mm pitting corrosion diameter.
 (a)
(a) (b)
(b) (c)
(c)
Figure 10. (a)-(c) Principal stress and deflection results of 80 mm pitting corrosion diameter.
SOLID 95
SHELL 181
 (a)
(a)  (b)
(b) (c)
(c)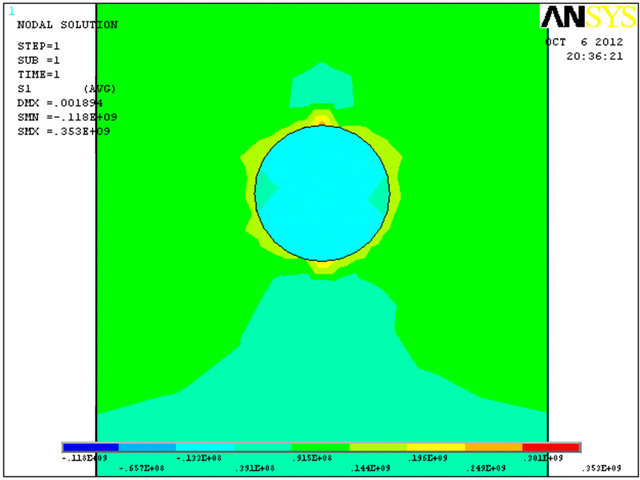 (d)
(d)
Figure 11. (a)-(d) Principal stress and deflection comparison between shell and solid elements.
Table 4. Cantilever beam repair results.

homogeneously behavior of the stress flow that leads to concentration reduction.
6. Conclusions
F. E. analysis is very effective tool to use in order to understand the pitting corrosion mechanical behavior. ANSYS program is used in this study since it presents a plain and simple way to study the behavior of cantilever beam pitting corrosion.
The influence of hemispherical pitting corrosion shape
Table 5. Bernoulli-Euler vs Cantilever beam repair results.

on cantilever beam has been studied by F. E. analysis in the context of stress failure (comparing to yield stress) and maximum deflection allowance. Three types of hemisphere radii were examined (30 mm, 60 mm, 80 mm). The M. S. decreasing is caused by corrosion diameter increasing since cross section reduction causes to stress concentration.
Also, compatibility between maximum principal stress
 (a)
(a) (b)
(b)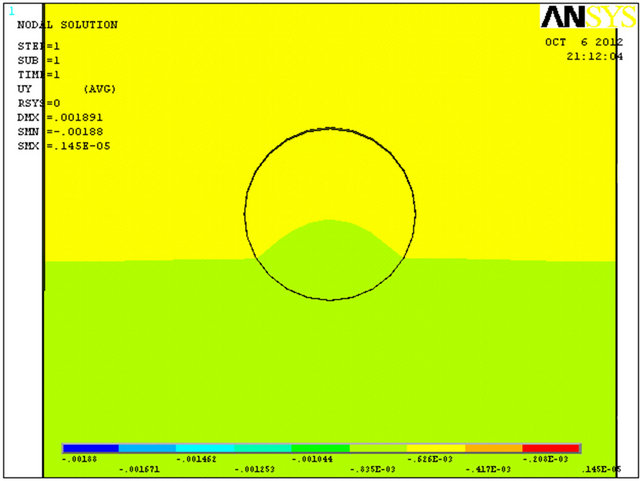 (c)
(c) (d)
(d)
Figure 12. (a)-(d) Regular surface repair results.
 (a)
(a)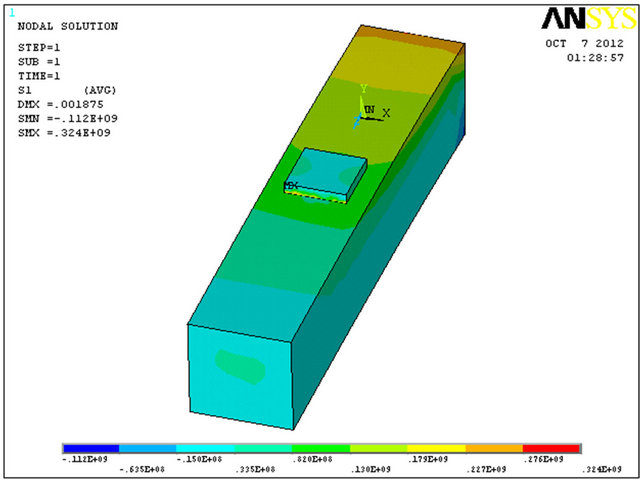 (b)
(b) (c)
(c)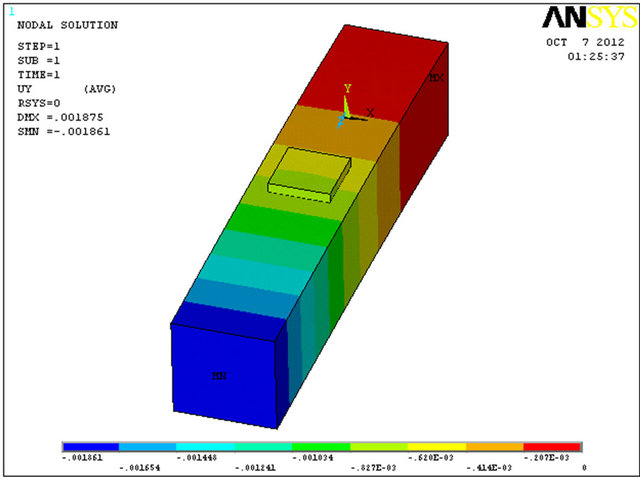 (d)
(d)
Figure 13. (a)-(d) Surface extension repair results.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 14. (a)-(d) “Handy Removal” repair results.
and deflection to Bernoulli-Euler theory was found only for small radius of the hemispherical corrosion shape (30 mm). Possible explanation was given by saying that Bernoulli assumption (“cross-sectional planes during bending deformation remain planes and perpendicular to the neutral axis”) is no longer necessarily valid for increasing diameter of pitted corrosion.
Moreover, examination of pitting corrosion repair was examined by using F. E. analysis. Three methods of repair have been investigated: 1) Regular surface repair; 2) Extension surface repair; and 3) “Handy Removal”.
Due to cross section reduction, the removal repair method is found to be with minimal M. S. value while surface extension repair method is with the maximal M. S. value.
In addition, agreement with Bernoulli-Euler theory for the three repairs was found only for extension surface repair (3.8% error) but for regular surface and handy removal repairs it was found to be inadequate (about 27% and 40% error respectively). Possible explanation for this phenomenon is due to the repair surface effectiveness; by connecting to as many nodes as possible, the repair surface area is large enough to cause homogeneously behavior of the stress flow that leads to concentration reduction.
7. Acknowledgements
The author gratefully acknowledges the financial support by Technion—Israel institute of Technology.
REFERENCES
- D. W. Hoeppner, “Pitting Corrosion: Morphology and Characterization,” NATO-RTO-AG-AVT-140, 2011.
- W. P. Zhang, H. C. Dai, X. L. Gu and S. N. Wu, “Effects of Corrosion Pits on Mechanical Properties of Corroded Steel Bars,” Earth and Space 2010: Engineering, Science, Construction, and Operations in Challenging Environments, 2010, pp. 3504-3511.
- V. Piprani, P. Samal, B. B. Verma and P. K. Ray, “Fatigue Life Estimation of Pre-Cprrpded Aluminum Alloy Specimen,” Thesis, National Institute of Technology, Rourkela, 2009.
- S. Chatterjee, S. Chatterjee and B. Doley, “Breathing Crack in Beam and Cantilever Using Contact Model Dynamic Analysis—A Study,” International Journal of Wisdom Based Computing, Vol. 1, No. 3, 2011, pp. 39-42.
- Z. H. M. E. Nouri, M. R. Khedmati and S. Sadeghifard, “An Effective Thickness Proposal for Strength Evaluation of One Side Pitted Steel Plates under Uniaxial Compression,” Latin American Journal of Solids and Structures, Vol. 9, No. 4, 2012, pp. 475-496. doi:10.1590/S1679-78252012000400004
- G. Xu, T. C. Ai and Q. Wang, “Simulation Analysis on Mechanical Properties for Corroded Deformed Steel Bar,” International Conference on Digital Manufacturing & Automation, Vol. 2, 2010, pp. 350-353.
- T. Potisuk, C. C. Higgins, T. H. Miller and C. Y. Solomon, “Finite Element Analysis of Reinforced Concrete Beams with Corrosion Subjected to Shear,” Advances in Civil Engineering, 2011, Article ID: 706803.
- Q. Zhang, X. Guo, N. Dai and P. Lu, “Corrosion and Fatigue Testing of Micro Sized 304 Stainless Steel Beams Fabricated by Femtosecond Laser,” Journal of Materials Science & Technology, Vol. 25, No. 2, 2009, pp. 187-193.
- J. M. Ruwan, S. Appuhamy, M. Ohga, T. Kaita and R. Dissanayake, “Reduction of Ultimate Strength Due to Corrosion—A Finite Element Computational Method,” International Journal of Engineering, Vol. 5, No. 2, 2011, pp. 194-207.
- ASTM G 46-94, 2005, “Standard Guide for Examintion and Evaluation of Pitting Corrosion”.
- “Military Handbook—MIL-HDBK-5H: Metallic Materials and Elements for Aerospace Vehicle Structures,” 5th Edition, Department of Defense, USA, 1998,
- ANSYS, INC., “ANSYS 10.0 Information Documents,” 2005.

