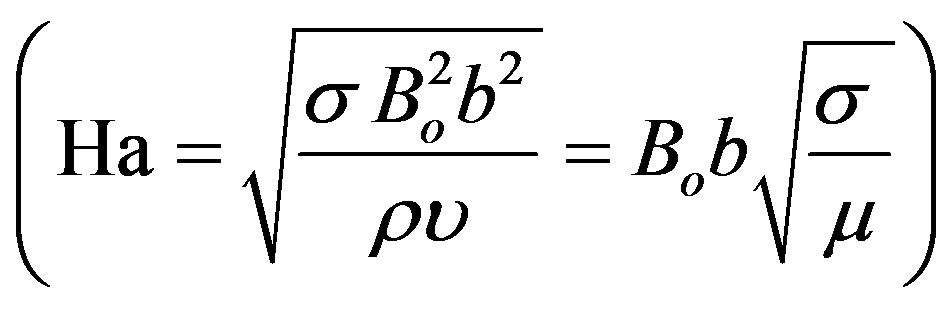World Journal of Mechanics
Vol.2 No.3(2012), Article ID:19984,7 pages DOI:10.4236/wjm.2012.23015
Mathematical Analysis of Unsteady MHD Blood Flow through Parallel Plate Channel with Heat Source
Basic Engineering Sciences Department, Faculty of Engineering, Elmenoufia University, Shibin El Kom, Egypt
Email: eldesokyi@yahoo.com
Received March 6, 2012; revised April 5, 2012; accepted April 20, 2012
Keywords: Blood Flow; Parallel Plate Channel; Boundary Layer; Heat Source; Magnetic Field
ABSTRACT
In the present study, a mathematical model of unsteady blood flow through parallel plate channel under the action of an applied constant transverse magnetic field is proposed. The model is subjected to heat source. Analytical expressions are obtained by choosing the axial velocity; temperature distribution and the normal velocity of the blood depend on y and t only to convert the system of partial differential equations into system of ordinary differential equations under the conditions defined in our model. The model has been analyzed to find the effects of various parameters such as, Hartmann number, heat source parameter and Prandtl number on the axial velocity, temperature distribution and the normal velocity. The numerical solutions of axial velocity, temperature distributions and normal velocity are shown graphically for better understanding of the problem. Hence, the present mathematical model gives a simple form of axial velocity, temperature distribution and normal velocity of the blood flow so that it will help not only people working in the field of Physiological fluid dynamics but also to the medical practitioners.
1. Introduction
The study of blood flow has been carried out by several authors. During the last decades extensive research work has been done on the fluid dynamics of biological fluids in the presence of magnetic field. For multiple reasons, applications of magnetohydrodynamics in physiological flow problems are of growing interest. Many researchers have reported that the blood is an electrically conducting fluid [1-4]. The electromagnetic force (Lorentz force) acts on the blood and this force opposes the motion of blood and there by flow of blood is impeded, so that the external magnetic field can be used in the treatment of some kinds of diseases like cardiovascular diseases and in the diseases with accelerated blood circulation such as hemorrhages and hypertension.
In general, biological systems are affected by an application of external magnetic field on blood flow through human arterial system. Many mathematical models have already been investigated by several research workers to explore the nature of blood flow under the influence of an external magnetic field. Tzirtzilakis [5] studied a mathematical model of biomagnetic fluid dynamics (BFD), suitable for the description of the Newtonian blood flow under the action of magnetic field. This model is consistent with the principles of ferrodynamics and magnetohydrodynamics and takes into account both magnetization and electrical conductivity of blood. Ramamurthy and shanker [6] studied magnetohydrodynamic effects on blood flow through a porous channel. They considered the blood a Newtonian fluid and conducting fluid.
Arterial MHD pulsatile flow of blood under periodic body acceleration has been studied by Das and Saha [7]. The blood flow in very narrow capillaries under the effect of transverse magnetic field has been investigated by Madhu et al. [8]. In this investigation; it is assumed that there is a lubricating layer between red blood cells and tube wall. A pulsatile flow of blood which is considered as a couple stress fluid through a porous medium under the influence of periodic body acceleration in the presence of magnetic field has been investigated by Rathod and Tanveer [9]. Singh and Rathee [10] gave an analytical solution of two-dimensional model of blood flow with variable viscosity through an indented artery due to low density lipoprotein effect in the presence of magnetic field. The investigation shows that hypertensive patients are more adequate to have heart circulatory problems. The effect of uniform transverse magnetic field on its pulsatile motion through an axi-symmetric tube is analyzed by Dulal and Ananda [11]. Zamir and Roach [12] studied Blood flow downstream of a two-dimensional bifurcation with a symmetrical steady flow.
Heat transfer in biological systems is relevant in many diagnostic and therapeutic applications that involve changes in temperature. As we know, the cardiovascular system is sensitive to changes in the environment, and flow characteristics of blood are modified to satisfy changing demands of the orgasm. In addition to transporting of oxygen, metabolites and other dissolved sub stances to and from the tissues, blood flow alters heat transfer within the body. Adhikary and Misra [13] pre sented an exact solution of the problem of oscillatory flow of a fluid and heat transfer along a porous oscillating channel in presence of an external magnetic field. The influence of blood flow in large vessels on the temperature distribution in hyperthermia has been developed by Lagendijk [14]. The blood flow in a small tube was modeled by the two-fluid model by Wang [15]. The flow is fully developed, constant heat flux convective heat transfer.
In the present investigation, a mathematical model for the unsteady blood flow through a very narrow parallel plate channel with heat source and external transverse magnetic field is presented. This work is an extensive study of Madhu et al. [8] with heat transfer under the conditions defined in our model. The main aim of this work is to obtain analytical expressions for axial velocity, temperature distribution and normal velocity using new boundary conditions and with converting the system of partial differential equations into system of ordinary differential equations. Also to study the effect of magnetic field (Hartmann number (Ha)), heat source parameter ( ) and Prandtl number (Pr) on the axial velocity, temperature distribution and normal velocity. Hence, the present mathematical model gives a simple form of axial velocity, temperature distribution and normal velocity of the blood flow so that it will help not only people working in the field of Physiological fluid dynamics but also to the medical practitioners. In fact, we studied the mathematical model in [2] with few modifications, also we checked the analytical solution and modified the results.
) and Prandtl number (Pr) on the axial velocity, temperature distribution and normal velocity. Hence, the present mathematical model gives a simple form of axial velocity, temperature distribution and normal velocity of the blood flow so that it will help not only people working in the field of Physiological fluid dynamics but also to the medical practitioners. In fact, we studied the mathematical model in [2] with few modifications, also we checked the analytical solution and modified the results.
2. Formulation of the Problem
Consider flow between non-conducting two parallel plates as shown in Figure 1.
Here blood is supposed to be Newtonian, incompressible, homogenous and viscous fluid. Also, the viscosity of blood is considered to be constant. The effect of mag netic field is considered in this model which is applied in a direction perpendicular to the flow of blood.
Considering u and v as velocity components in the directions of x and y respectively (axial and normal respectively) at time t in the flow field, we may write the two dimensional boundary layer equations in presence of transverse magnetic field as
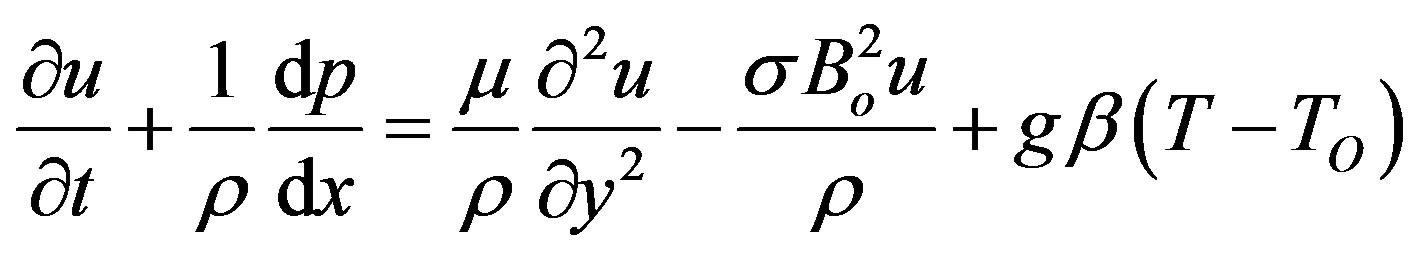 (1)
(1)
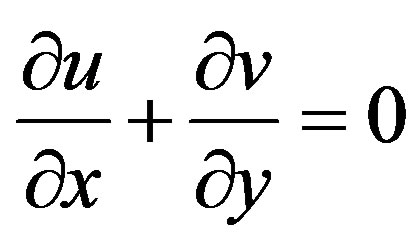 (2)
(2)

Figure 1. Geometry of the model.
 (3)
(3)
Introduce the following non-dimensional variables
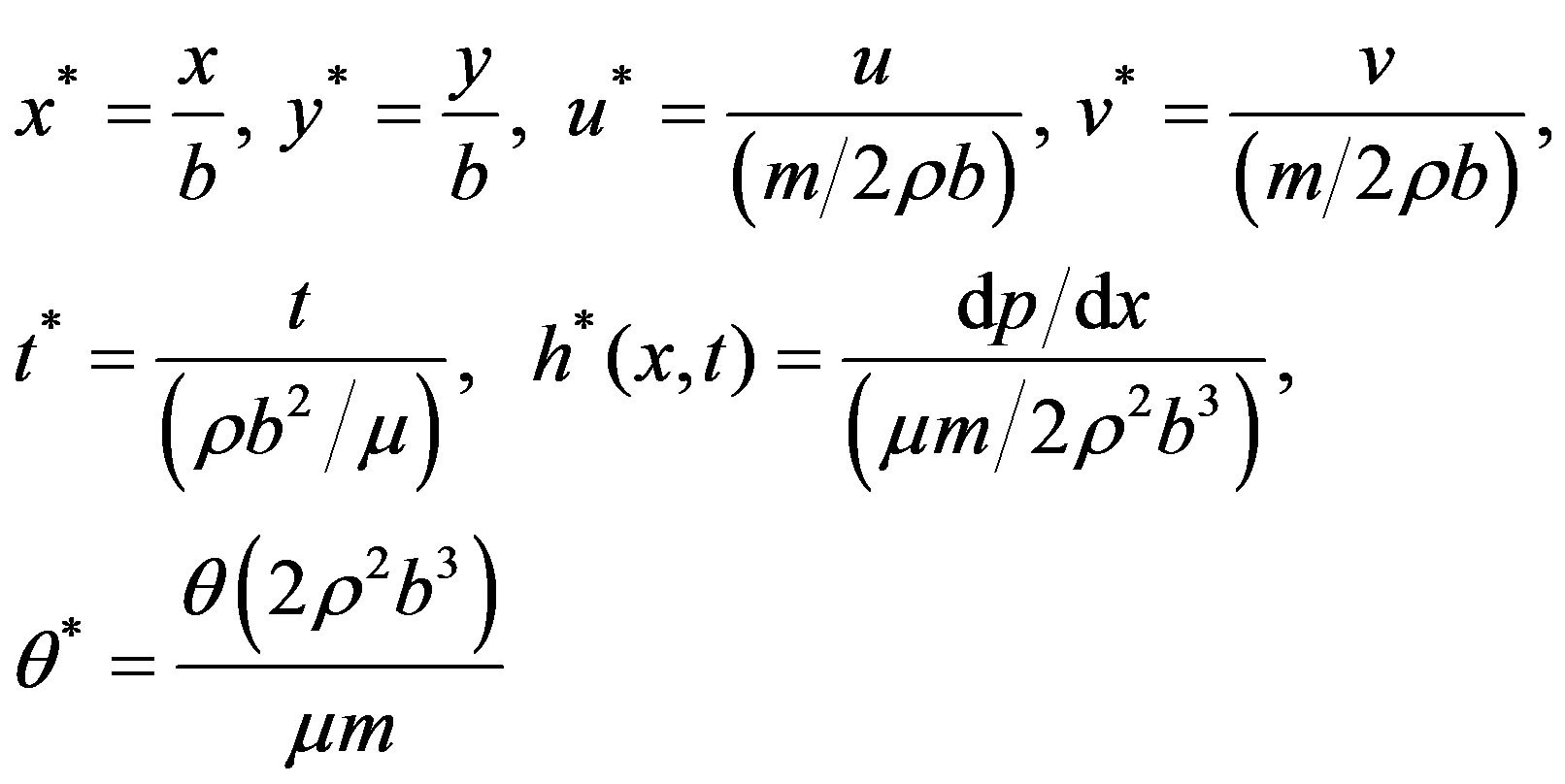 (4)
(4)
Substituting from Equation (4) into the Equations (1)- (3) we may write these equations after dropping the stars as
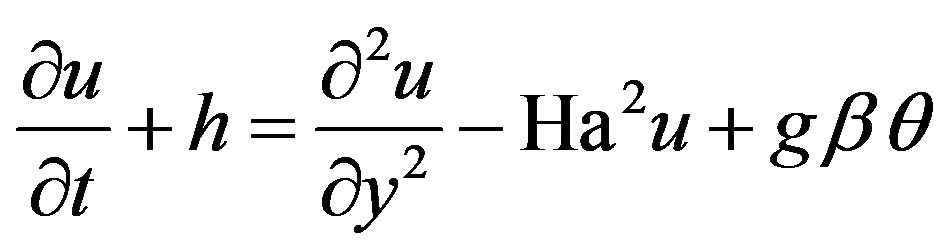 (5)
(5)
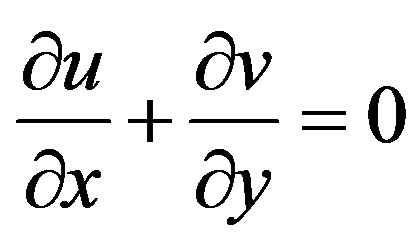 (6)
(6)
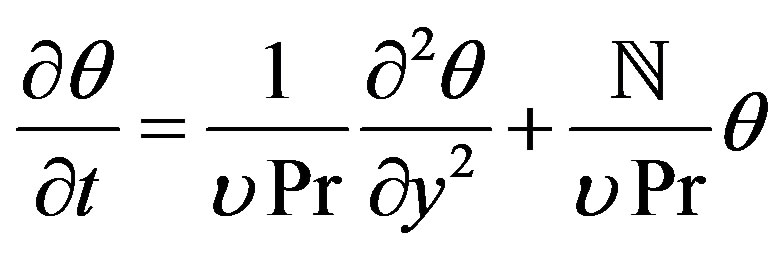 (7)
(7)
From Equation (7) we can observe that the temperature distribution  has 1st derivative with respect to time t. From this observation and with the help of solution of partial differential equation by separation of vari ables technique we can get the following equation
has 1st derivative with respect to time t. From this observation and with the help of solution of partial differential equation by separation of vari ables technique we can get the following equation
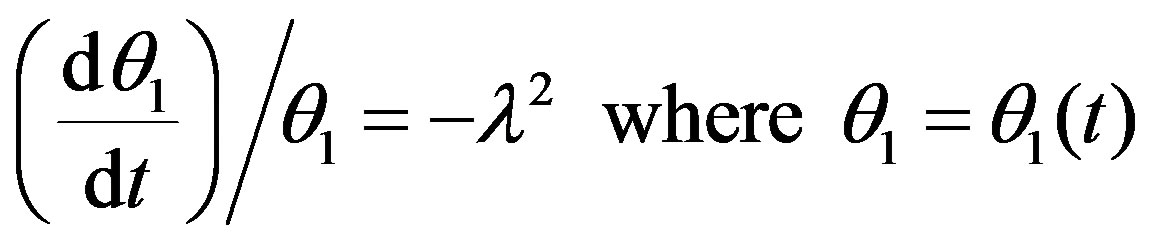
It is observed that the solution of this equation will be on the form .
.
Similarly, the axial velocity u has the same concept, and then the solution of the problem will take the form mentioned in Section 3 and the boundary conditions are taken as:
 (8)
(8)
3. Solution of the Problem
With the help of discussion in the previous section, let us choose the solutions of the Equations (5)-(7) respectively as
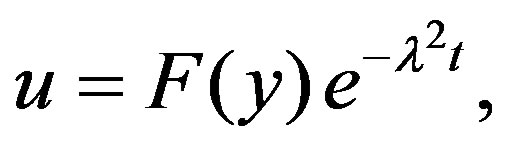 (9)
(9)
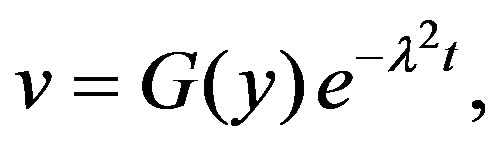 (10)
(10)
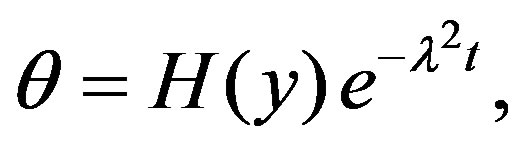 (11)
(11)
Substituting from Equations (9)-(11) into Equations (5)-(8) we obtain the following equations respectively
 (12)
(12)
where 
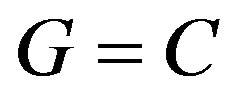 (A constant)(13)
(A constant)(13)
 (14)
(14)
The boundary conditions become:
 (15)
(15)
Solution of Equation (14) is as follows
 (16)
(16)
where .
.
Using the boundary conditions Equation (15) we obtain

Then the final form of H(y) is
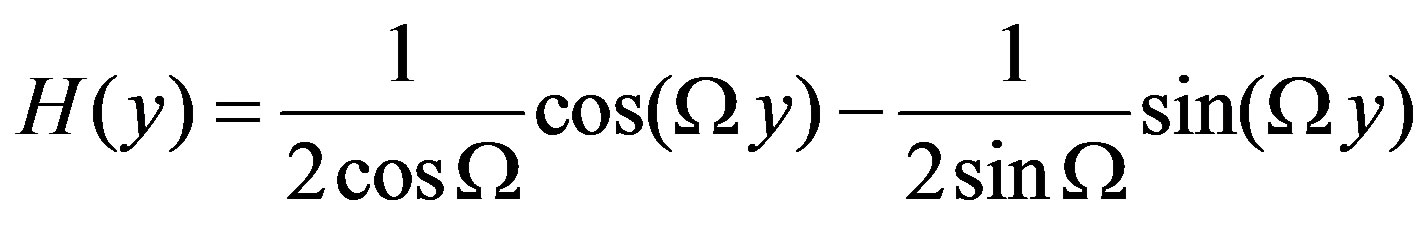 (17)
(17)
From Equation (11) and (17) then the temperature distribution is given by
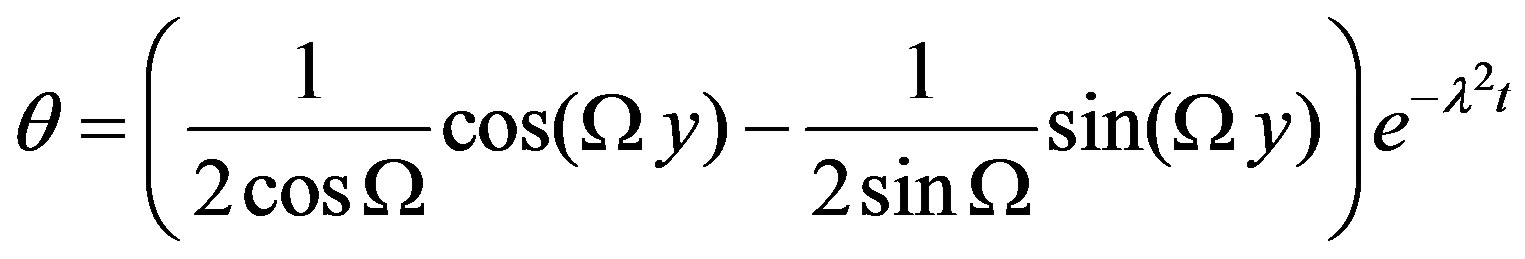 (18)
(18)
Substituting from Equation (17) into Equation (12) we get

Solving the last equation to obtain F using the Equation (15) as follows The Homogenous solution:

Substitute from Equation (15) to calculate the constants 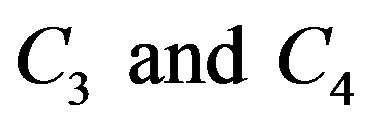


The particular solution is:
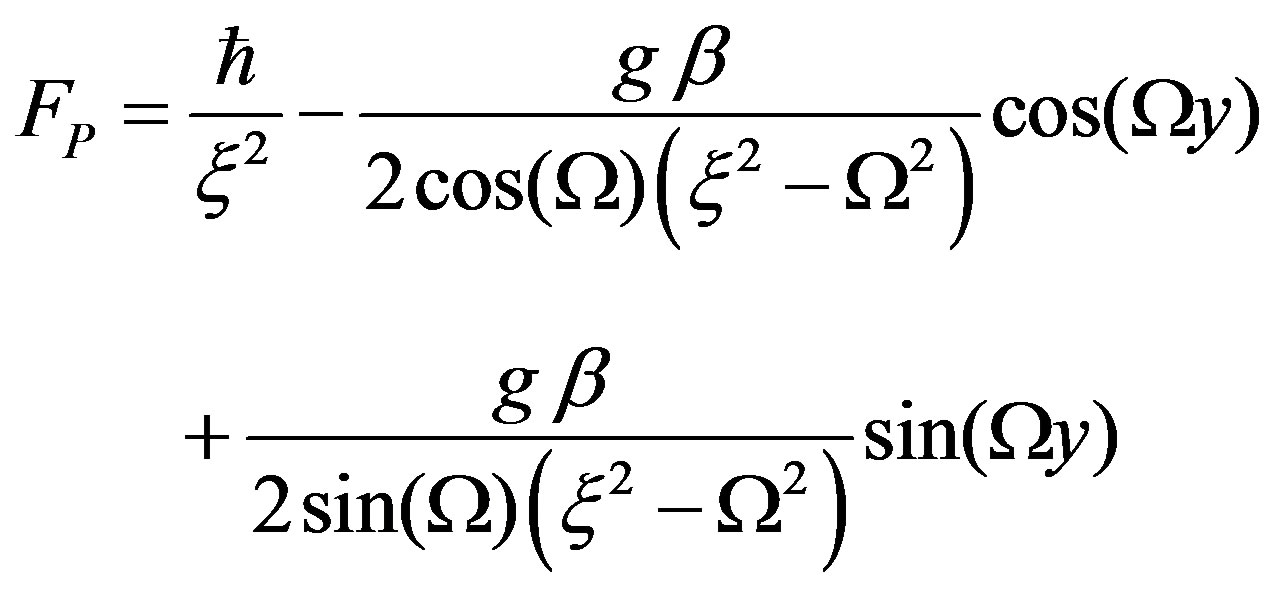
The general solution of F is
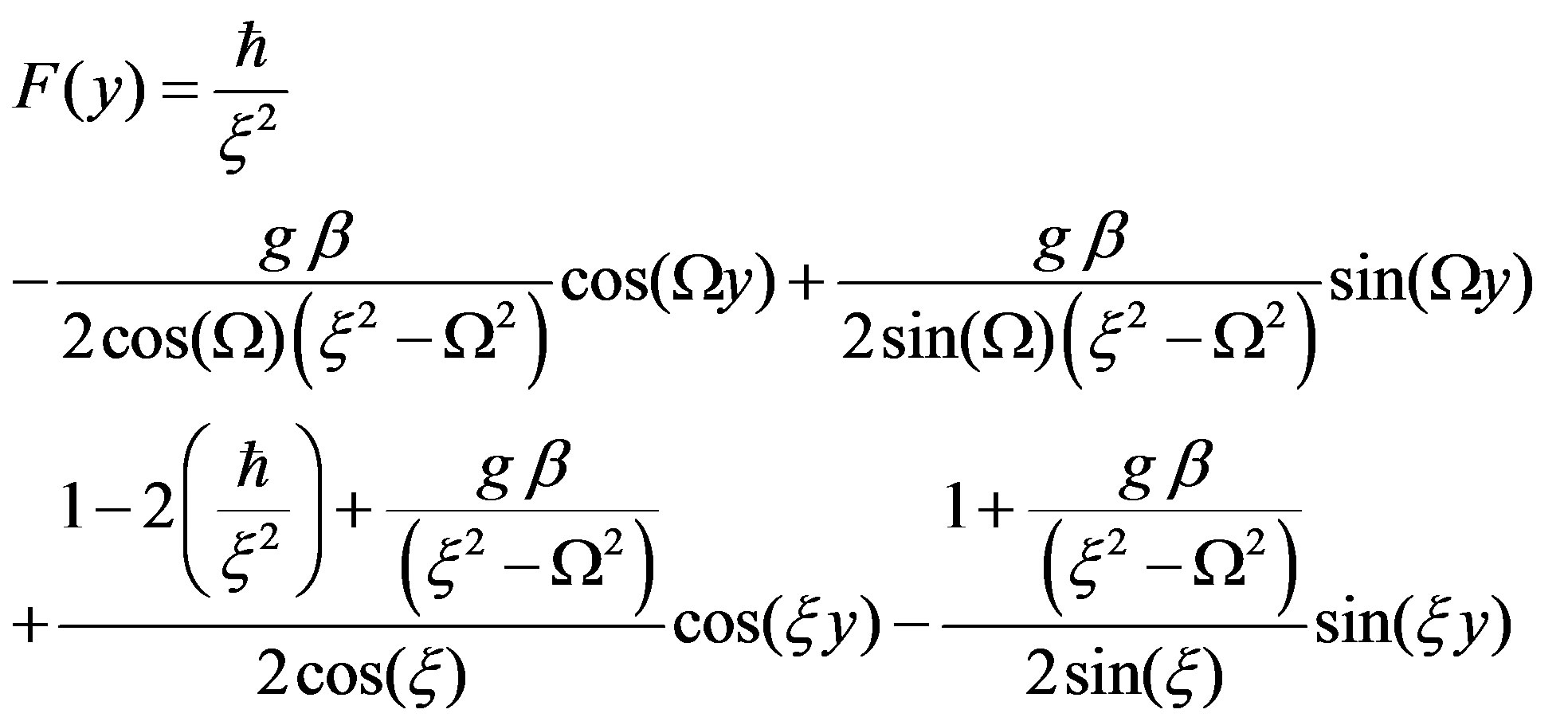 (19)
(19)
From Equation (9) and Equation (19) the axial velocity of blood is given by
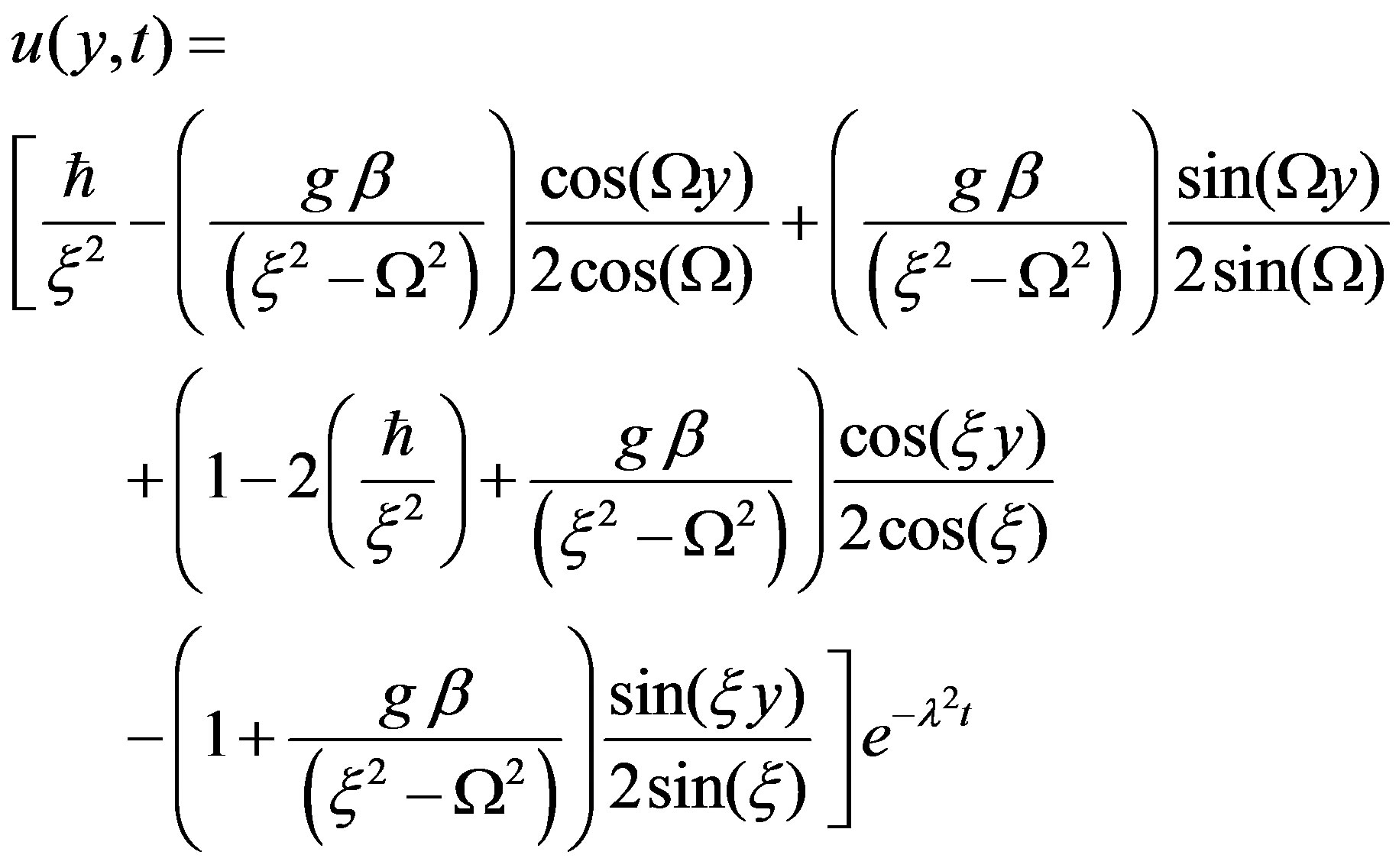 (20)
(20)
Also, from Equations (10) and (13) the normal velocity is given by
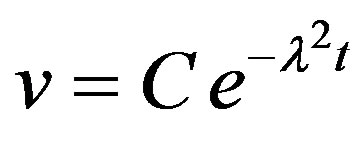 (21)
(21)
where C is an arbitrary constant (C = 1).
Equations (18), (20) and (21) show the temperature distribution, the axial velocity and normal velocity respectively.
4. Numerical Results and Discussion
The flow investigation has been carried out by studying the effect of individual factors like heat source and magnetic field. The main objective of the study is to find the role of heat source parameter, magnetic field (Hartmann number), Prandtl number and decay parameter on tem perature distribution, axial velocity and normal velocity. To observe these effects, numerical codes are developed for the numerical evaluations of the analytic results obtained.
In Figure 2 we study the variation of temperature distribution versus y at 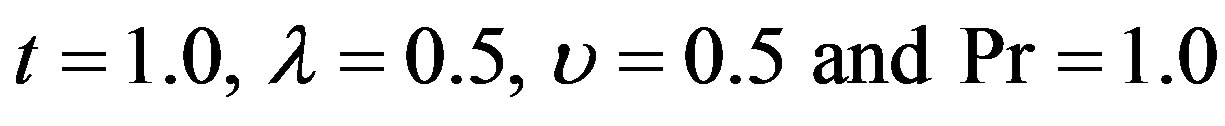 with different values of the heat source parameter (
with different values of the heat source parameter ( ). We observe that for the same value of y the temperature field increases with increasing the value of heat source parameter
). We observe that for the same value of y the temperature field increases with increasing the value of heat source parameter . Also, the temperature field increases to reach at its maximum value at y = 0 then decreases.
. Also, the temperature field increases to reach at its maximum value at y = 0 then decreases.
Figure 3 gives the temperature field distribution for different values of Prandtl number (Pr = 0.50, 1.00, 3.00, 5.00, 7.00) at . It is observed that the temperature field increases with increasing the value of Prandtl number Pr. The effect of Prandtl number is the same as heat source parameter. The effect of decay parameter on the temperature field distribution at
. It is observed that the temperature field increases with increasing the value of Prandtl number Pr. The effect of Prandtl number is the same as heat source parameter. The effect of decay parameter on the temperature field distribution at  is shown in Figure 4. It is shown that the temperature field decreases with increasing the decay parameter. The maximum effect of the decay parameter on the temperature field is at y = –1 and there is no effect approximately of the decay parameter on the temperature distribution at y = 1.
is shown in Figure 4. It is shown that the temperature field decreases with increasing the decay parameter. The maximum effect of the decay parameter on the temperature field is at y = –1 and there is no effect approximately of the decay parameter on the temperature distribution at y = 1.
Figure 5 gives the axial velocity distribution for different values of heat source parameter ( = 0.50, 0.75, 1.00, 1.25, 1.50) at
= 0.50, 0.75, 1.00, 1.25, 1.50) at 
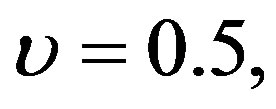

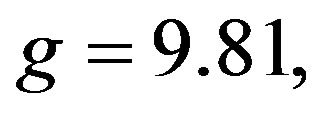 h = 0.50
h = 0.50  and
and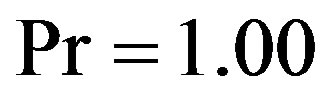 . It is observed that the axial velocity increases with increasing the heat source parameter
. It is observed that the axial velocity increases with increasing the heat source parameter .
.
The effect of magnetic field on the axial velocity for different values of Hartmann number (Ha = 1.00, 2.00, 3.00, 4.00, 6.00) is shown in Figure 6 at 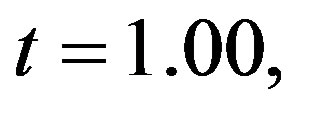
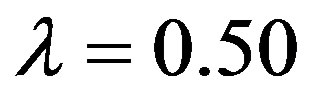 ,
, 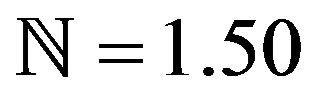

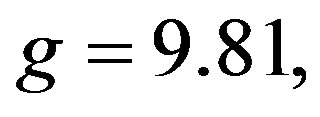
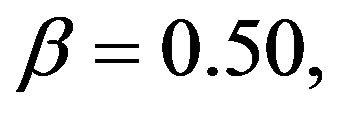
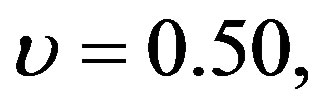 and
and . It is shown that the magnetic field decreases the axial velocity. We can observe that the axial velocity at
. It is shown that the magnetic field decreases the axial velocity. We can observe that the axial velocity at 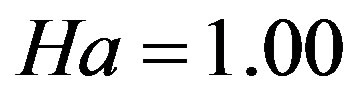 increases from y = –1
increases from y = –1

Figure 2. Temperature distribution for different values of heat source at t = 1.00, λ = 0.50, υ = 0.50 and Pr = 1.00.
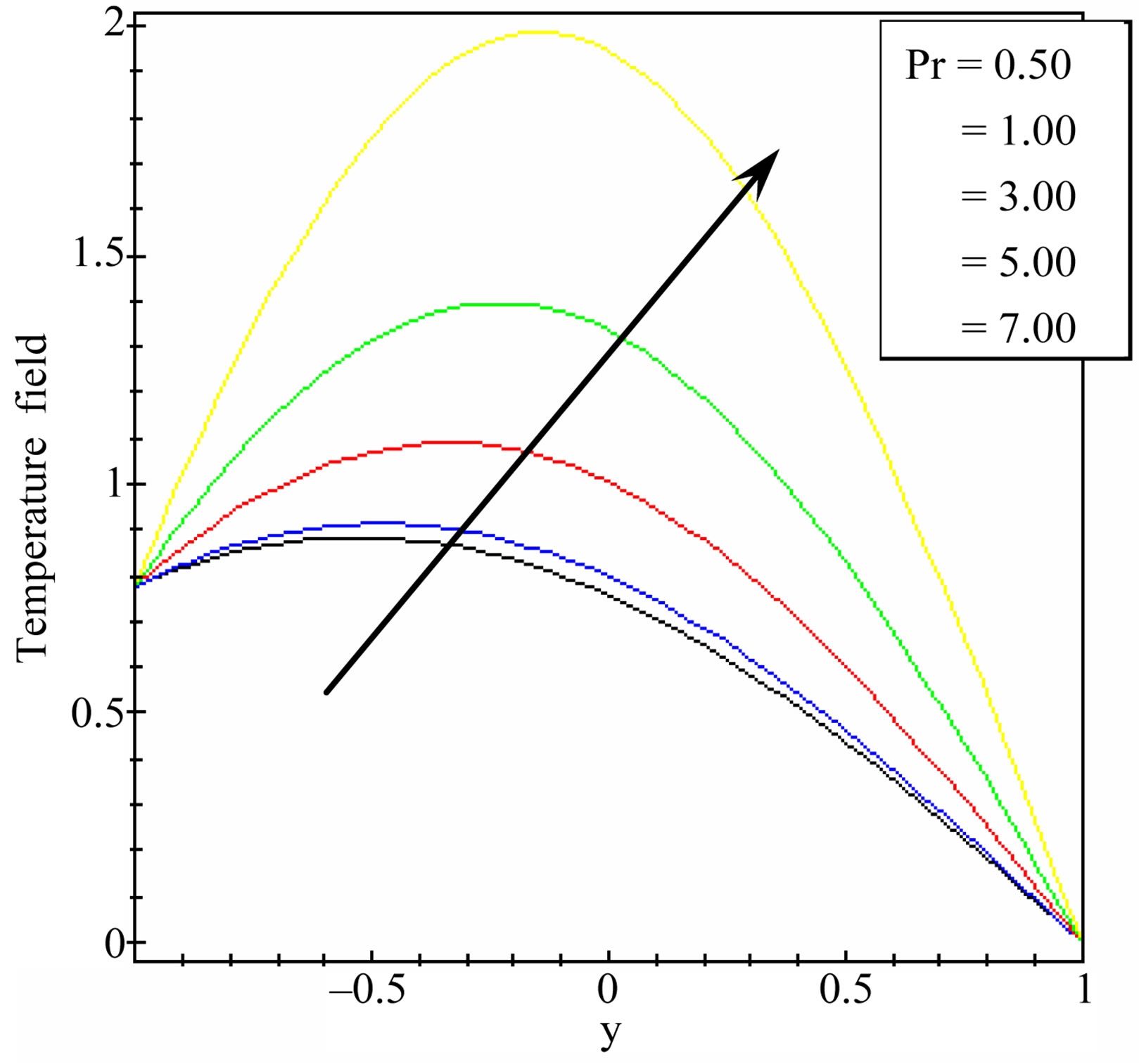
Figure 3. Temperature distribution for different values of Prandtl number at t = 1.00, λ = 0.50, υ = 0.50 and  = 1.00.
= 1.00.
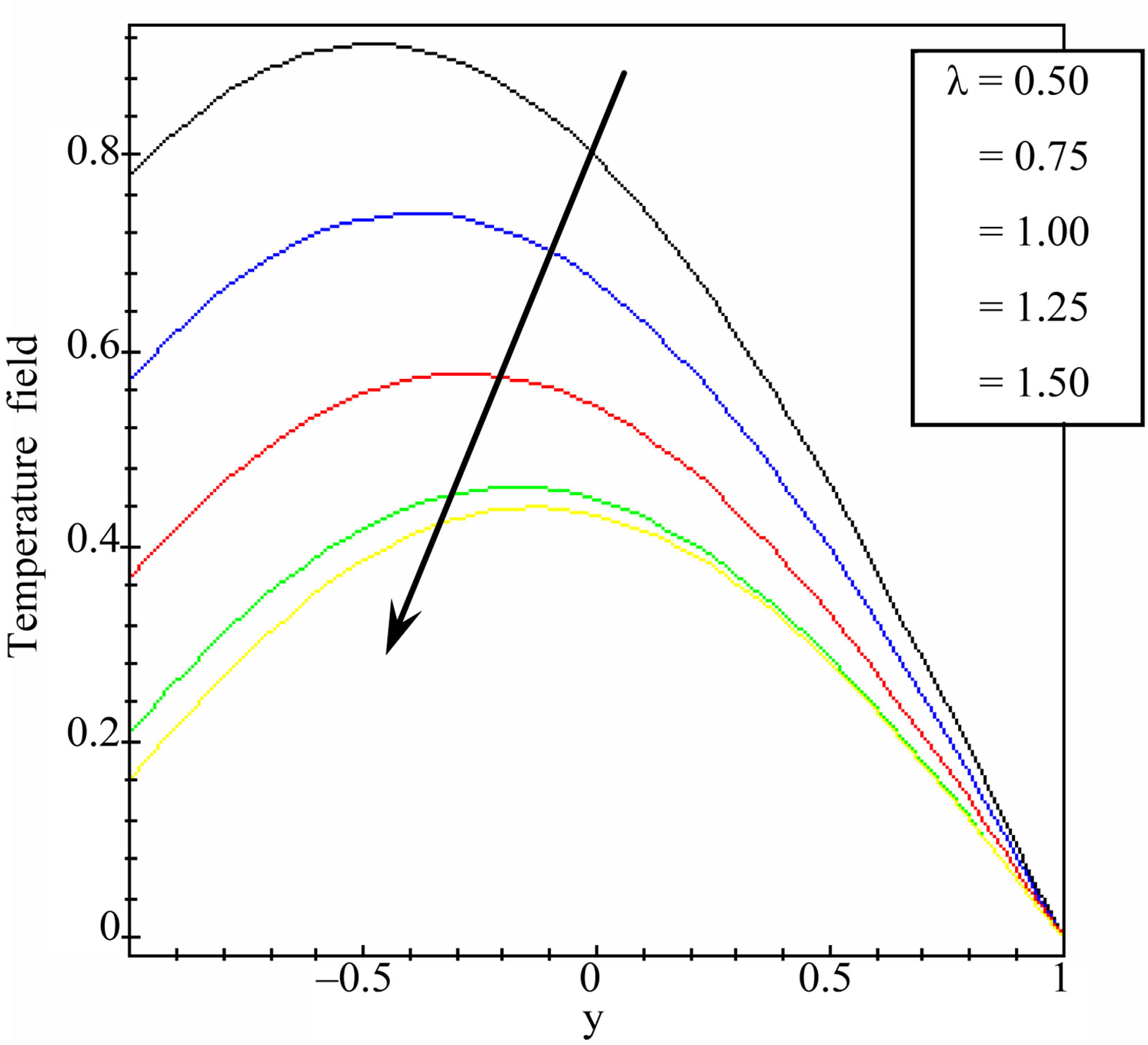
Figure 4. Temperature distribution for different values of decay parameter at t = 1.00, Pr = 1.00, υ = 0.50 and  = 1.00.
= 1.00.
and attains maximum at y = 0 then decreases until y = 1. While at  we observe that the axial velocity decreases along y.
we observe that the axial velocity decreases along y.
Figure 7 shows the effect of Prandtl number on the distribution of the axial velocity at 
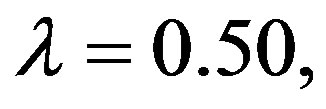
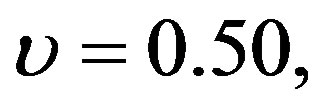
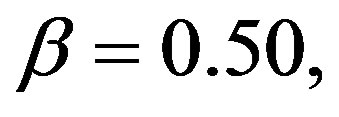 g = 9.81, h = 0.50,
g = 9.81, h = 0.50, 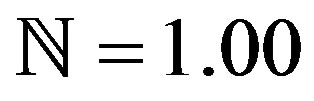 and
and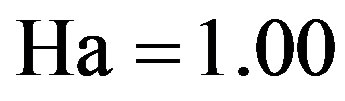 . It is shown that the axial velocity increases with increasing the prandtl number. The effect of decay parameter is indicated in Figure 8 at t = 1.00,
. It is shown that the axial velocity increases with increasing the prandtl number. The effect of decay parameter is indicated in Figure 8 at t = 1.00, 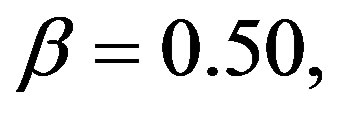
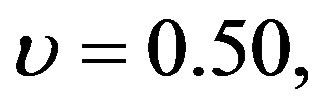
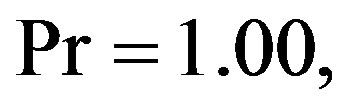 g = 9.81, h = 0.50,
g = 9.81, h = 0.50, 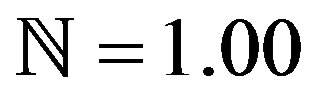 and
and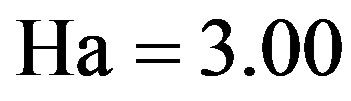 . The axial velocity decreases with increasing the decay parameter. The maximum effect of the decay parameter on the axial velocity is at y = –1 and the axial velocity approximately not affected by the decay parameter at y = 1.
. The axial velocity decreases with increasing the decay parameter. The maximum effect of the decay parameter on the axial velocity is at y = –1 and the axial velocity approximately not affected by the decay parameter at y = 1.
Figure 9 indicates the effect of decay parameter on the normal velocity distribution. It is shown that the normal velocity decreases with increasing the decay parameter. The normal velocity is decreases slowly at low values of the decay parameter ( ) while it is decreases very fast and tends to zero at high values of decay parameter (
) while it is decreases very fast and tends to zero at high values of decay parameter (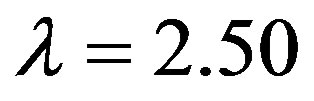 ).
).
5. Conclusions
In the present investigation, a mathematical model for the unsteady blood flow through a very narrow parallel plate channel with heat source and external transverse magnetic field is presented. This work is an extensive study of Madhu et al. [8] with heat transfer under the conditions defined in our model. The effect of magnetic field, heat source seems to be significant.
The main conclusions of the present paper may be summarized as follows:
• The present mathematical model gives a simple form of axial velocity, temperature distribution and normal velocity of the blood flow. Analytical expressions are
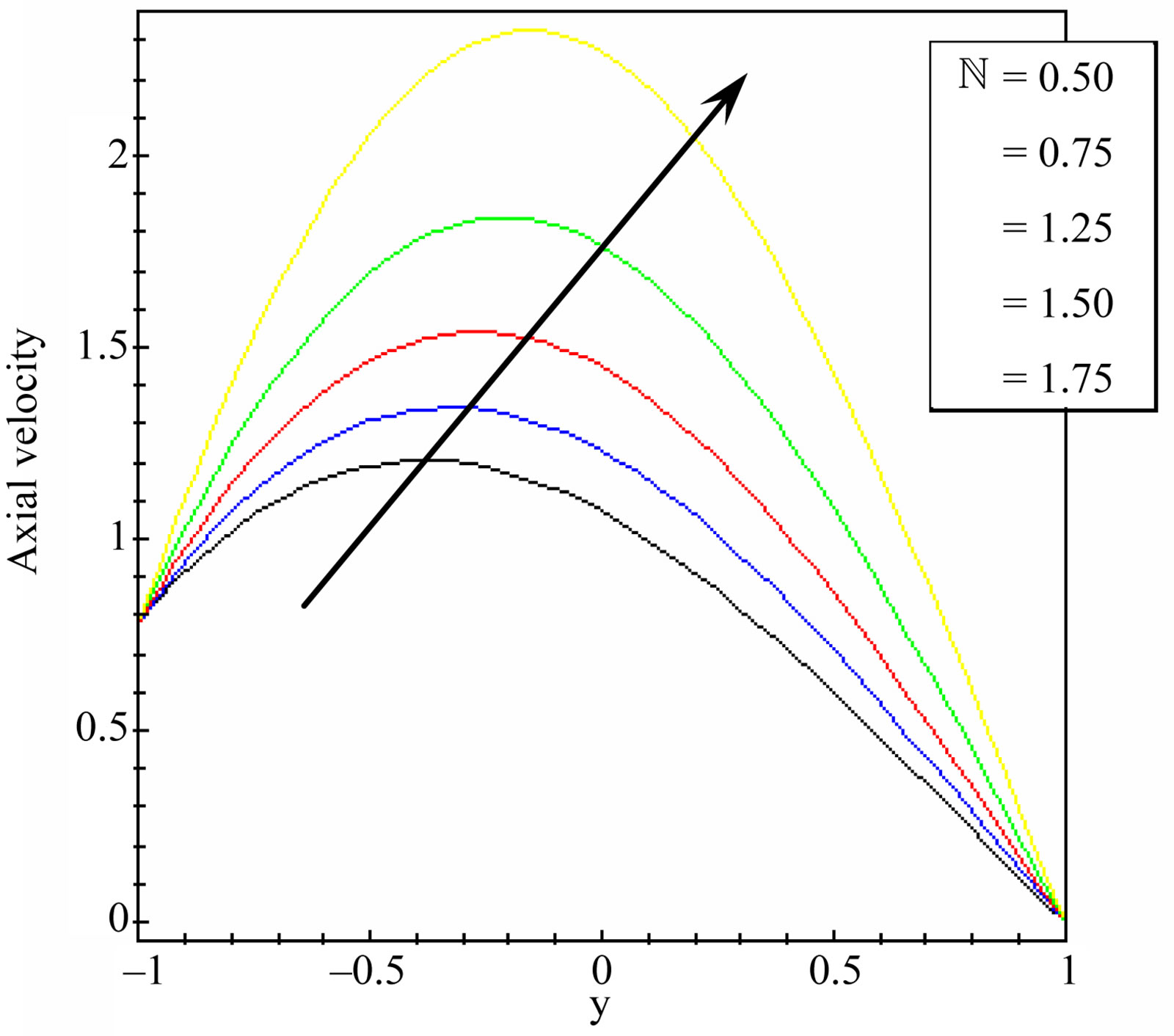
Figure 5. Axial velocity distribution for different values of heat source at t = 1.00, Pr = 1.00, υ = 0.50, λ = 0.50, h = 0.50, β = 0.50, g = 9.81 and Ha = 1.00.
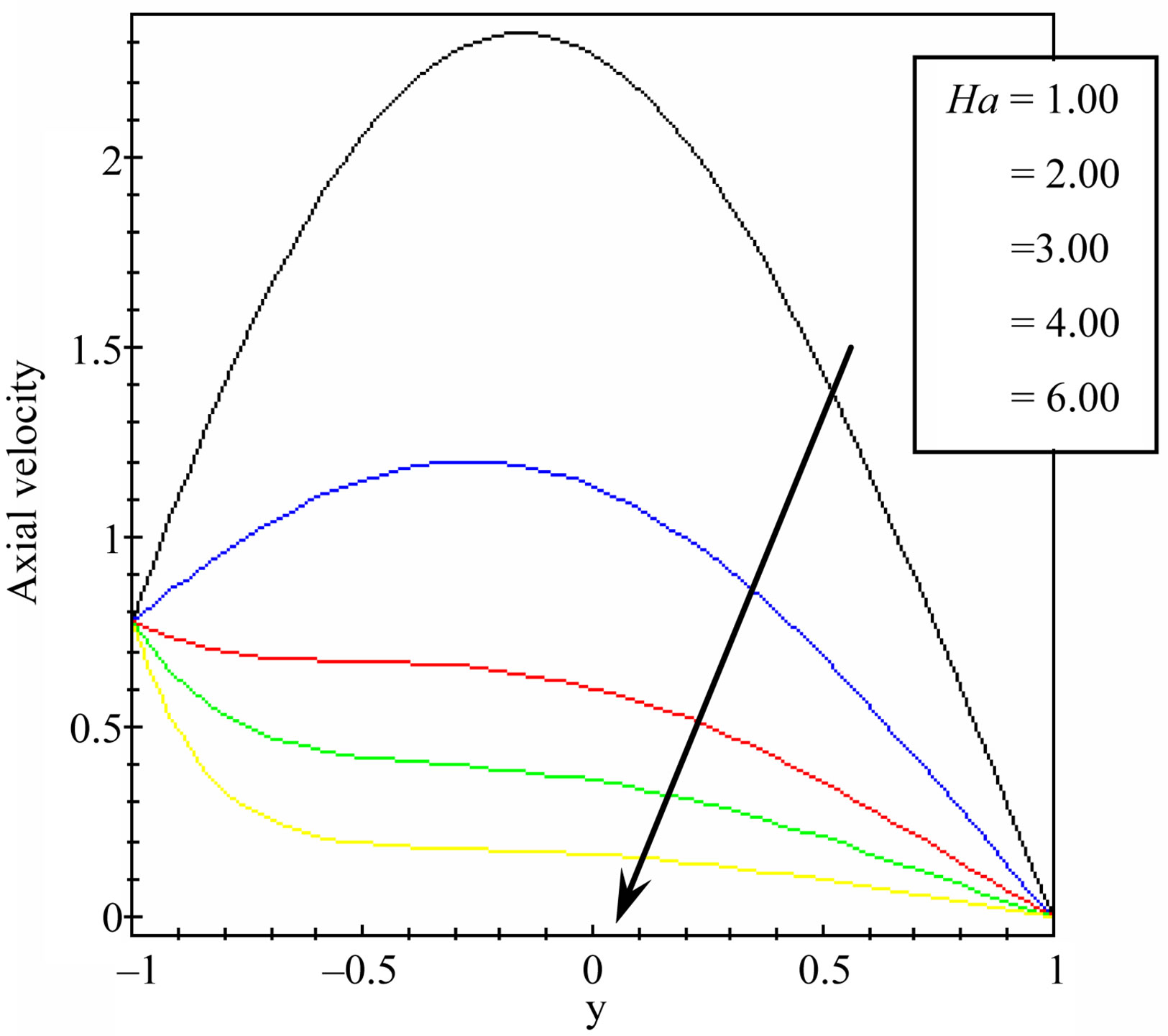
Figure 6. Axial velocity distribution for different values of Hartmann number at t = 1.00, Pr = 1.00, υ = 0.50, λ = 0.50, h = 0.50, β = 0.50, g = 9.81 and  = 1.50.
= 1.50.
Figure 7. Axial velocity distribution for different values of Prandtl number at t = 1.00, Ha = 1.00, υ = 0.50, λ = 0.50, h = 0.50, β = 0.50, g = 9.81 and  = 1.50.
= 1.50.
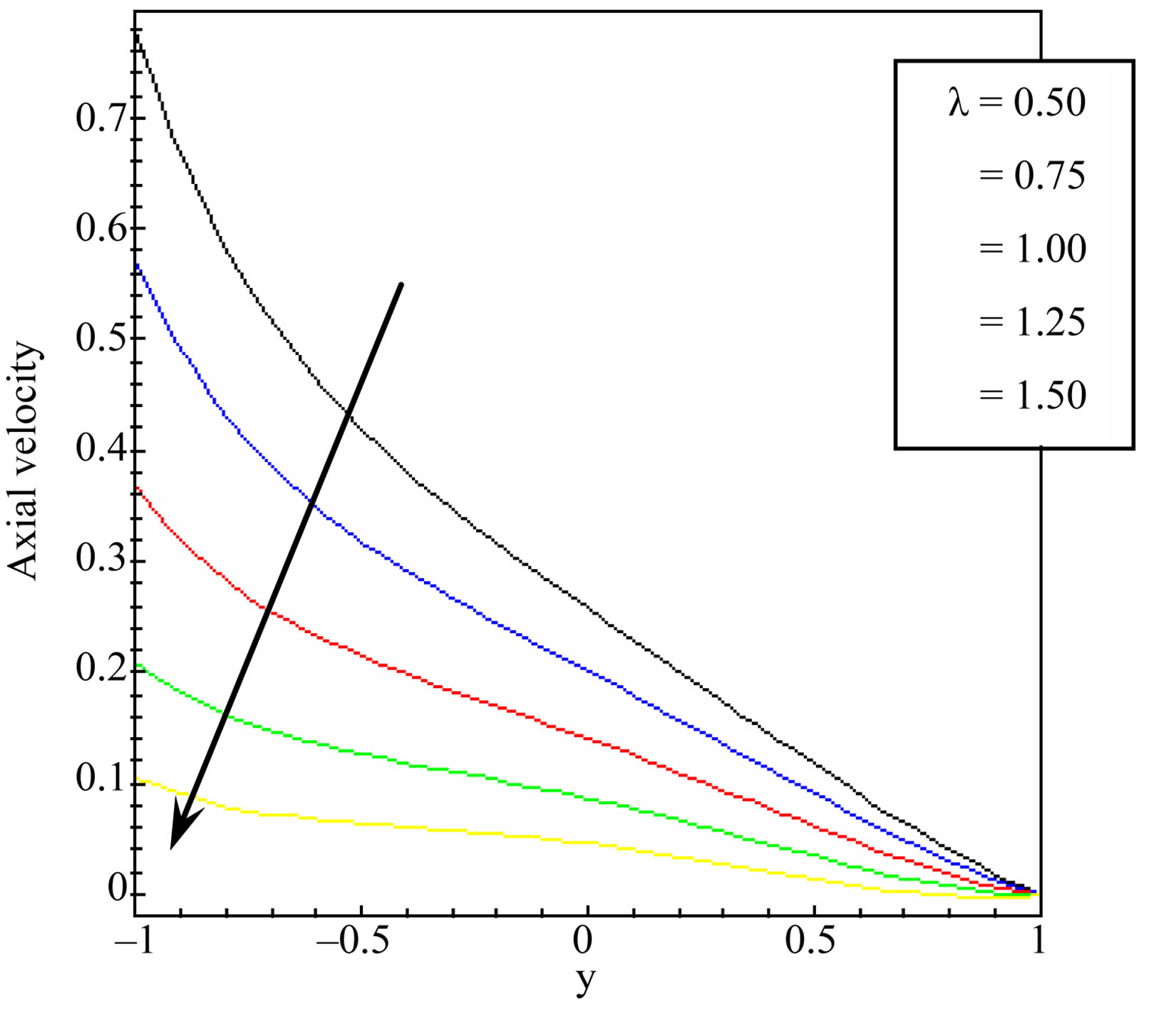
Figure 8. Axial velocity distribution for different values of decay parameter at t = 1.00, Ha = 3.00, υ = 0.50, Pr = 1.00, h = 0.50, β = 0.50, g = 9.81 and  = 1.00.
= 1.00.
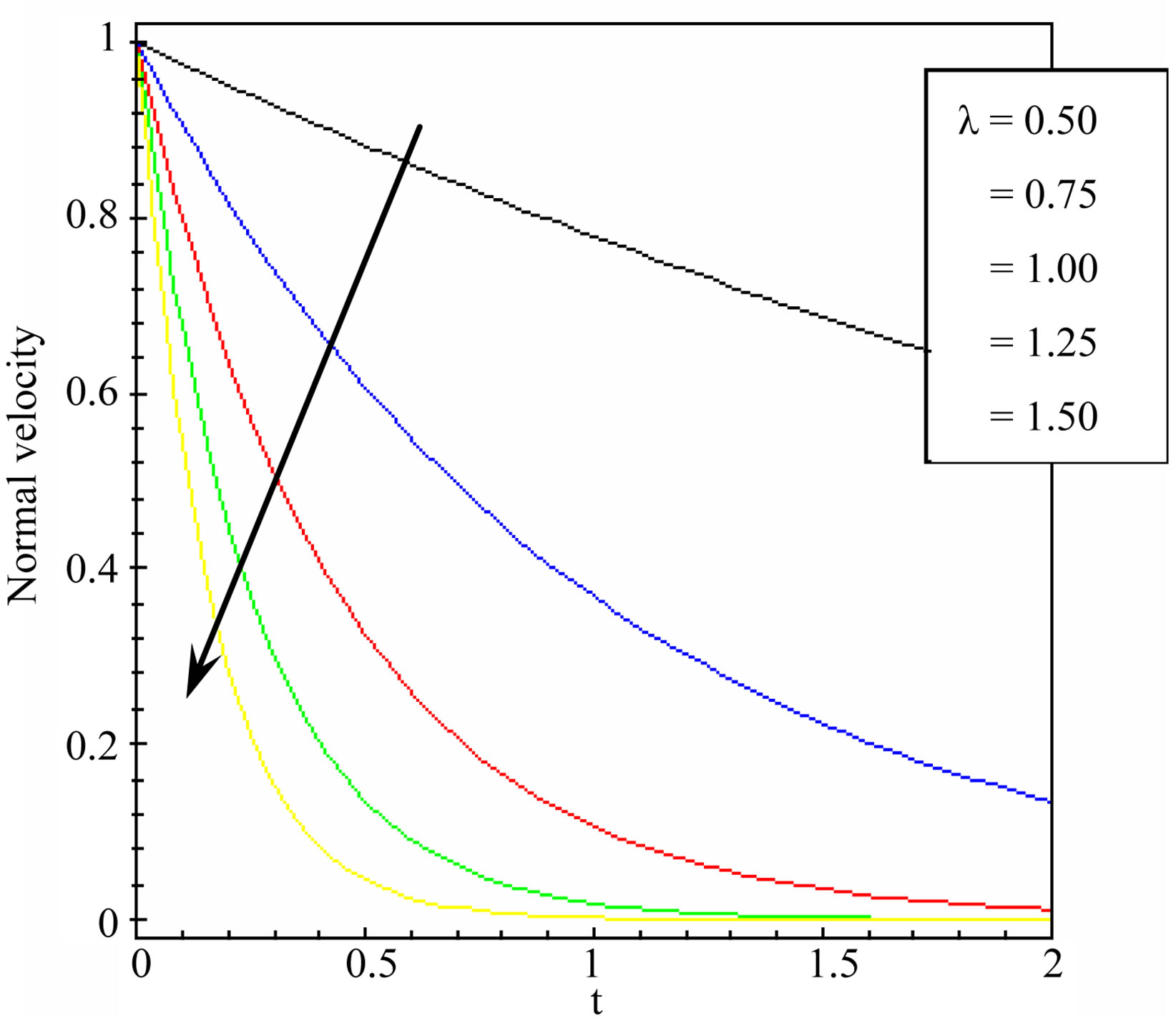
Figure 9. Normal velocity distribution for different values of decay parameter.
obtained by choosing the axial velocity; temperature distribution and the normal velocity of blood depend on y and t only along with corresponding boundary conditions to convert the system of partial differential equations into system of ordinary differential equations.
• The temperature field increases with increasing the heat source parameter and Prandtl number while decreases with increasing the decay parameter.
• The axial velocity increases with increasing heat source parameter and Prandtl number while decreases with increasing the Hartmann number and decay parameter.
• The normal velocity decreases with increasing the decay parameter and tending to zero very fast for higher values of the decay parameter.
Hence, the present mathematical model gives a simple form of axial velocity, temperature distribution and normal velocity of the blood flow so that it will help not only people working in the field of Physiological fluid dynamics but also to the medical practitioners.
6. Acknowledgements
The author would like to express deeply thankful to referee for providing valuable suggestions to improve the quality of the manuscript.
REFERENCES
- J. Singh and R. Rathee, “Analytical Solution of TwoDimensional Model of Blood Flow with Variable Viscosity through an Indented Artery Due to LDL Effect in the Presence of Magnetic Field,” International Journal of Physical Sciences, Vol. 5, No. 12, 2010, pp. 1857-1868.
- O. Prakash, S. P. Singh, D. Kumar and Y. K. Dwivedi, “A Study of Effects of Heat Source on MHD Blood Flow through Bifurcated Arteries,” AIP Advances, Vol. 1, No. 4, 2011, pp. 1-7. doi:10.1063/1.3658616
- N. Verma and R. S. Parihar, “Effects of Magneto-Hydrodynamic and Hematocrit on Blood Flow in an Artery with Multiple Mild Stenosis,” International Journal of Applied Mathematics and Computer Science, Vol. 1, No. 1, 2009, pp. 30-46.
- D. C. Sanyal, K. Das and S. Debnath, “Effect of Magnetic Field on Pulsatile Blood Flow through an Inclined Circular Tube with Periodic Body Acceleration,” Journal of Physical Science, Vol. 11, 2007, pp. 43-56.
- E. E. Tzirtzilakis, “A Mathematical Model for Blood Flow in Magnetic Field,” Physics of Fluids, Vol. 17, No. 7, 2005, p. 077103. doi:10.1063/1.1978807
- G. Ramamurthy and B. Shanker, “Magnetohydrodynamic Effects on Blood Flow through Porous Channel,” Medical and Biological Engineering and Computing, Vol. 32, No. 6, 1994, pp. 655-659. doi:10.1007/BF02524242
- K. Das and G. C. Saha, “Arterial MHD Pulsatile Flow of Blood under Periodic Body Acceleration,” Bulletin of Society of Mathematicians Banja Luka, Vol. 16, 2009, pp. 21-42.
- M. Jain, G. C. Sharma and A. Singh, “Mathematical Analysis of MHD Flow of Blood in Very Narrow Capillaries,” International Journal of Engineering Transactions B: Applications, Vol. 22, No. 3, 2009, pp. 307-315.
- V. P. Rathod and S. Tanveer, “Pulsatile Flow of Couple Stress Fluid through a Porous Medium with Periodic Body Acceleration and Magnetic Field,” Bulletin of the Malaysian Mathematical Sciences Society, Vol. 32, No. 2, 2009, pp. 245-259.
- J. Singh and R. Rathee, “Analytical Solution of TwoDimensional Model of Blood Flow with Variable Viscosity through an Indented Artery Due to LDL Effect in the Presence of Magnetic Field,” International Journal of Physical Sciences, Vol. 5, No. 12, 2010, pp. 1857-1868.
- C. S. Dulal and B. Ananda, “Pulsatile Motion of Blood through an Axi-Symmetric Artery in Presence of Magnetic Field,” Journal of Science and Technology of Assam University, Vol. 5, No. 2, 2010, pp. 12-20.
- M. Zamir and M. R. Roach, “Blood Flow Downstream of a Two-Dimensional Bifurcation,” Journal of Theoretical Biology, Vol. 42, No. 1, 1973, pp. 33-42. doi:10.1016/0022-5193(73)90146-X
- S. D. Adhikary and J. C. Misra, “Unsteady Two-Dimensional Hydromagnetic Flow and Heat Transfer of a Fluid,” International Journal of Applied Mathematics and Mechanics, Vol. 7, No. 4, 2011, pp. 1-20.
- J. J. W. Lagendijk, “The Influence of Blood Flow in Large Vessels on the Temperature Distribution in Hyperthermia,” Physics in Medicine and Biology, Vol. 27, No. 1, 1982, p. 17. doi:10.1088/0031-9155/27/1/002
- C. Y. Wang, “Heat Transfer to Blood Flow in a Small Tube,” Journal of Biomechanical Engineering, Vol. 130, No. 2, 2008, p. 024501. doi:10.1115/1.2898722
Nomenclature
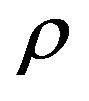 : Density of blood
: Density of blood
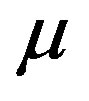 : Dynamic viscosity of the blood (constant)
: Dynamic viscosity of the blood (constant)
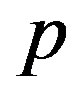 : Pressure of blood
: Pressure of blood
 : Electrical conductivity of the blood
: Electrical conductivity of the blood
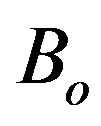 : Intensity of the magnetic field
: Intensity of the magnetic field
 : Gravitational acceleration
: Gravitational acceleration
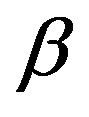 : Coefficient of volume expansion due to temperature
: Coefficient of volume expansion due to temperature
 : Temperature of blood
: Temperature of blood
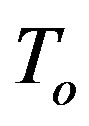 : Temperature of the wall (fixed temperature)
: Temperature of the wall (fixed temperature)
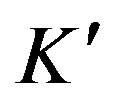 : Coefficient of the thermal conductivity
: Coefficient of the thermal conductivity
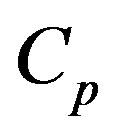 : Specific heat at constant pressure
: Specific heat at constant pressure
 : Quantity of heat
: Quantity of heat
 : Temperature distribution
: Temperature distribution 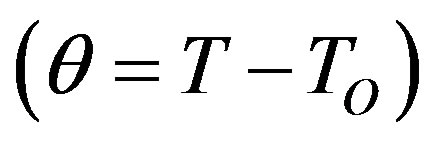
 : Decay parameter
: Decay parameter
 : Kinematic viscosity
: Kinematic viscosity 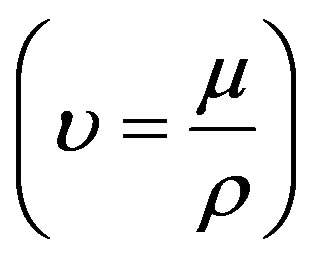
 : Prandtl number
: Prandtl number 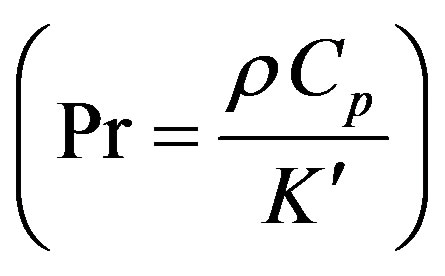
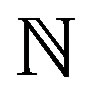 : Heat source parameter
: Heat source parameter 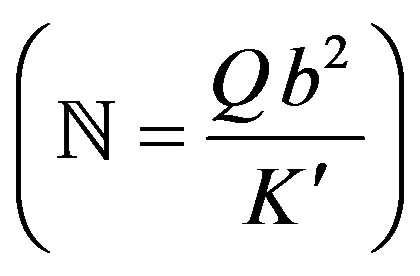
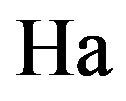 : Hartmann number
: Hartmann number