World Journal of Mechanics
Vol.2 No.4(2012), Article ID:21534,7 pages DOI:10.4236/wjm.2012.24022
Computational Fluid Dynamics Analysis of Greenhouses with Artificial Heat Tube
1Department of Engineering, Universidade de Trás-os-Montes e Alto Douro, Vila Real, Portugal
2Department of Mechanical Engineering and Applied Science, University of Pennsylvania, Philadelphia, USA
3Research Department of Agriculture Secretary, Lisbon, Portugal
Email: rouboa@seas.upenn.edu
Received April 24, 2012; revised May 30, 2012; accepted June 10, 2012
Keywords: Greenhouses; Artificial Heating Tubes; CFD; Finite Element Method
ABSTRACT
With the workmanship decrease in farms, the necessity to rationalize the use of other inputs and the development of technology has rapidly expanded the use of computer simulation in agricultural systems. One of the agricultural systems in which the modeling process of plant growth has been more engaged is the greenhouse production for horticultural crops. In Mediterranean climate, it is during the night that the energy losses are important and can be compensated with an artificial heat input. In this work an experiment was performed in a greenhouse in the north of Portugal. Temperature values in several points and air velocity in the aperture were measured during the night for three different cases: natural convective heating (case A); artificial heating tubes (AHT) (case B); AHT and natural ventilation (case C). A CFD simulation, carried out using FLOTRAN module of ANSYS, was also performed in two-dimensional configuration to obtain the indoor air temperature and velocity fields for the three cases. A very good agreement between experimental and numerical temperature values were verified, which allows to validate the adopted numerical procedure. In case A, the average temperature was 2.2˚C. An average increase of 6.7˚C and 3.5˚C on the air temperature was obtained for the case B and case C, respectively. These results clearly emphasis the influence of each thermal load on greenhouse indoor air properties.
1. Introduction
In contrast to most agricultural production systems, greenhouses enable the growth and productivity of crops to be manipulated by controlling the indoor climate. A greenhouse is a closed space surrounded by translucent walls allowing better internal environmental conditions than the natural ones. In fact, greenhouses are widely used in the whole world due to their low cost. The airflow, the temperature and humidity vary strongly inside these closed spaces and depend of the outside climate.
The temperature inside the greenhouses is controlled by heating systems. These heating equipments depend partially on the fuel source available as natural gas, fuel oil, diesel, or kerosene. Natural gas is the cleanest of the petroleum fuels and the most efficient to use without cost effective [1]. The exhaust gases from all heating systems contain combustion products that can cause damages on plants seedlings. Other products cause similar damage by emitting sulphur dioxide and nitric oxide. Several researchers are trying to optimize fertilization process to solve environmental problems.
Temperature, humidity, CO2, solar radiation and air velocity determines the greenhouse microclimate. These variables are affected by the external weather, by the properties of the greenhouse cover, and by the properties of the plants.
In Portugal the greenhouses are covered by polyethylene rather than glass, therefore the heat losses by radiation at night could be considerable, especially in conditions of cloudless sky [2].
In Mediterranean climate, the radiation frost is dominant and is responsible for significant damages in horticulture crops during winter and earlier spring. This occurs often in Portugal because, generally, greenhouses do not have heating systems.
Simulation of environmental conditions in greenhouses is a powerful tool in modern horticulture. The heat ventilation process is the driving force for the air circulation and temperature distribution in greenhouses [3].
Several studies on natural ventilation were based on estimations of a global air exchange rate [4] and simulations of air temperature and a global vegetation temperature using a big leaf model [5,6] and energy balance methods [7].
In all these methods several heat transfer coefficients are assumed empirically and they are not able to clearly mapping airflow patterns and temperature profiles.
Meanwhile, some progress in flow modelling by computational fluid dynamics (CFD), in air circulation and temperature measurements, has recently been made for a closed greenhouse [4] and in a two-span naturally ventilated greenhouse [8]. Up till now, very few studies detailed climate in full-scale greenhouses heated by Artificial Heat Tube (AHT) have been conducted by both experiments and modeling.
In this work an experiment was performed in a polyethylene covered greenhouse in night conditions in the north of Portugal, and for three different cases:
• Case A: natural convective heating (no heater and no natural ventilation effect);
• Case B: AHT—artificial heating tubes (with heater and no natural ventilation effect);
• Case C: AHT and natural ventilation (heater and natural ventilation effect).
The measured temperature values should indicate the influence of each thermal load in the indoor air properties and allows the validation of several numerical procedures. The FLOTRAN module of ANSYS is used to obtain the indoor air temperature and velocity fields. This module performs CFD simulations using the finite element method, therefore a coupled differential equations system are solved, which means that it is only needed to validate one of the air properties to accept as reliable all the others.
2. Materials and Methods
2.1. Experimental Set up
The experimental greenhouse (22 m length, 8.5 m width and 3.5 m height), located in the north of Portugal, is cover with a polyethylene sheet and have traditional discontinuous vent openings on the top. A schematic view of the experimental greenhouse is shown in Figure 1.
Temperature at several positions along the paths was measured by thin thermocouples. The coordinates of the nodes for five paths are shown in Figure 1. This will be of great significance later on the result analysis.
Since this region is characterized by a predominant
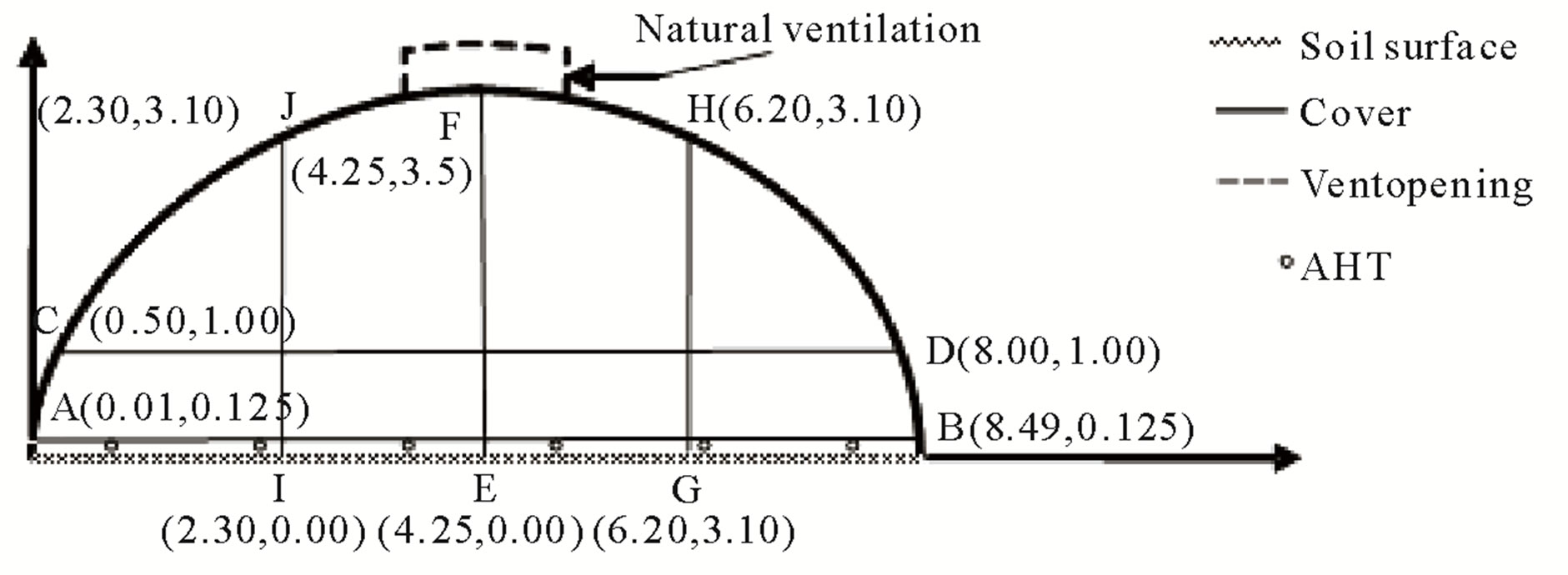
Figure 1. Schematic design of the experimental greenhouse and coordinates of nodes.
northerly wind, channeled by a small valley, symmetric airflow was assumed along the direction with respect to each opening. Therefore, a transversal section was selected to explore the flow patterns and the external air speed and temperature were measured by two three-dimensional sonic anemometers.
It is during the night that the energy losses are important and can be compensated with an artificial heat input. On the other hand, in this type of climate, the energetic contribution from solar radiation usually avoids heating during the day. During sunny days, it is usually necessary to ventilate greenhouses for limiting temperature elevations, and therefore to prevent the prejudicial limit (biological maximum) to be reached.
The classical heating systems are designed exclusively for the greenhouse aerial ambient. Although, the plant growth is intensively affected by its aerial environment, some physiological problems in winter cultivations are caused by inappropriate soil thermal conditions. These conditions can decrease the nutrient absorption process. On the other hand, if the greenhouse floor is heated, it will become into a source of heat to the environment. Therefore, in our experiment the heating system is composed by polyethylene tubes arranged on the floor into which hot water flows from a hot spring originated from geothermal aquifer.
2.2. Mathematical Model
The energy exchange between greenhouse and environment are complex, they can be summarized by:
• Thermal radiation from the soil, atmosphere, greenhouse environment and vegetation, emitted through greenhouse structure and cover;
• Natural convection of the indoor air;
• Forced convection caused by wind flow;
• Conduction in soil and cover.
The greenhouse indoor air flow is turbulent, therefore an adequate mathematical model avoiding the use of empirical heat transfer coefficients should be performed. Incompressible Reynolds averaged Navier-Stokes equations with the k-e model is used, also because it provides adequate CPU (Computing Process Unit) time and residual values [9].
This model was implemented in FLOTRAN module of ANSYSâ. According to these variables, the continuity equation, momentum conservation equations, turbulent and dissipated energy (k-e) conservation equations, for an incompressible fluid in Cartesian coordinates, are written in conservative form as [10]:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
The parameters used in k-ε model are presented in Table 1.
2.3. Resolution Method
The numerical method used by ANSYSâ is based on Finite Element Method. The steady solution of the governing equations is given in each square element of the discretized whole domain. In order to solve the linear system, TDMA (Tri-Diagonal Matrix Algorithm) is used as solver [11]. Two-dimensional (Vx and Vy) velocities, pressure, turbulence kinetic energy (k) and turbulence kinetic energy dissipation ratio are a DOF (degrees of freedom) for each element. The convergence criteria of TDMA are 10–5 for the two component velocities Vx and Vy, and 10–3 for pressure, turbulence kinetic k and turbulence energy dissipation ratio e.
The ANSYSâ module, FLOTRAN, allow solve easily the two-dimensional system equations cited above. The
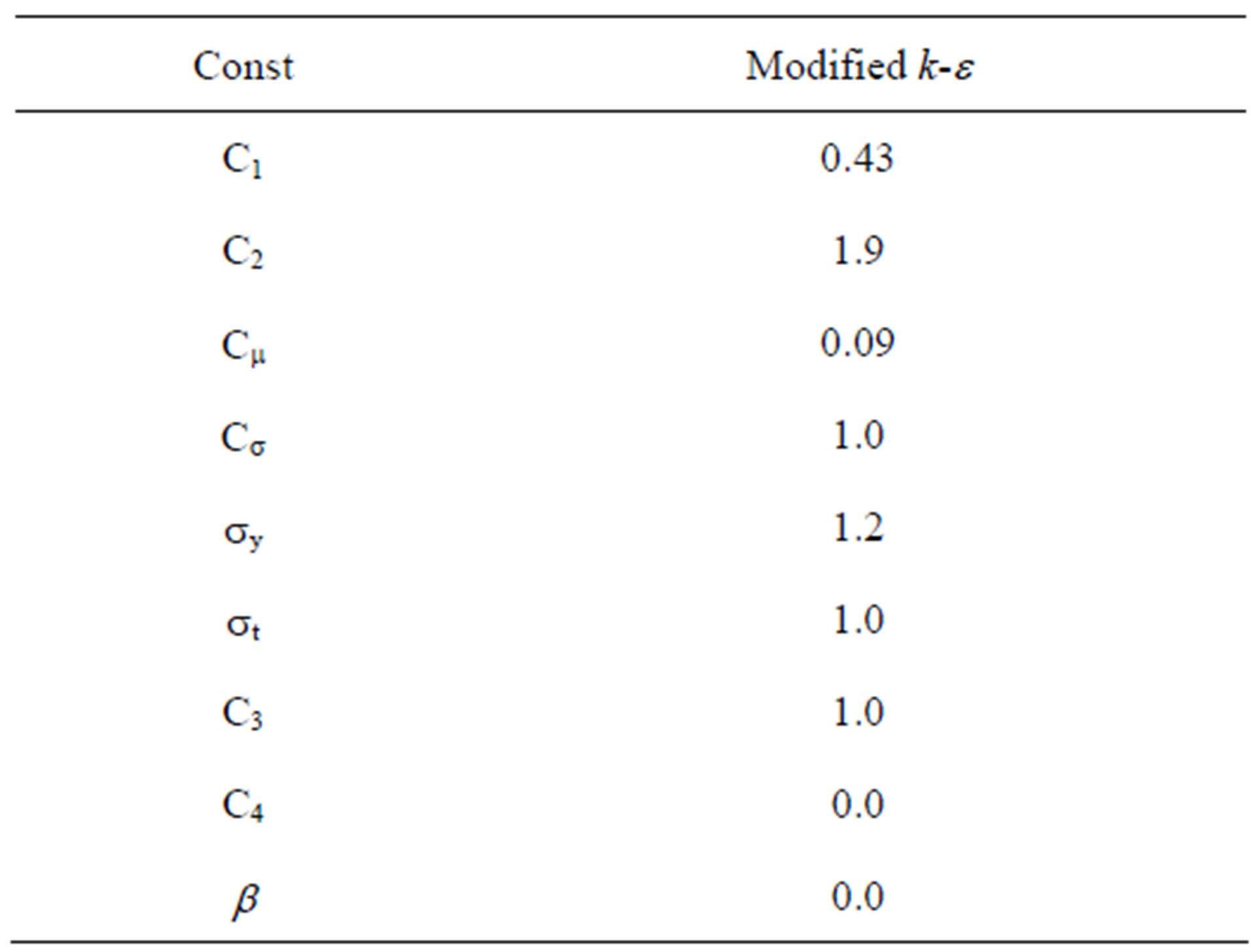
Table 1. Modified k-e model constants.
obtained solutions are pressure, temperature and velocity distribution in a single-phase. For each element, ANSYSâ code calculates velocity components, pressure, and temperature from the conservation of three properties: mass, momentum, and energy.
The requirements of meshes for turbulence model are more restrictive than those for laminar flow. Due to this fact, the “quad” element size has to be about 0.025 m. In the zone of higher gradients of temperature, velocities or pressure, in particular near the walls, the mesh size has to be refined with a factor of four as seen in Figure 2.
2.4. Boundary Conditions
In Table 2 are presented the boundary conditions (Dirichlet kind) used for each case.
• Development of the flow near outlet boundaries.
2.5. Stability Analysis
The convergence and numerical stability was obtained by observing the rate of change of the solution on the monitor and the behavior of relevant dependent variables during the iterations (Ite). Controlled variables were: velocity (V), pressure (P), temperature (T), and turbulence quantities such as kinetic energy (degree of freedom ENKE) and kinetic energy dissipation rate (ENDS).
The convergence monitors (CM) are a normalized measure of the solutions rate of change from iteration to iteration. Denoting by the general field variable, f, any DOF, the convergence monitor is defined as follows [9]:
 (5)
(5)

Figure 2. Element mesh of the 2-D model of the greenhouse.
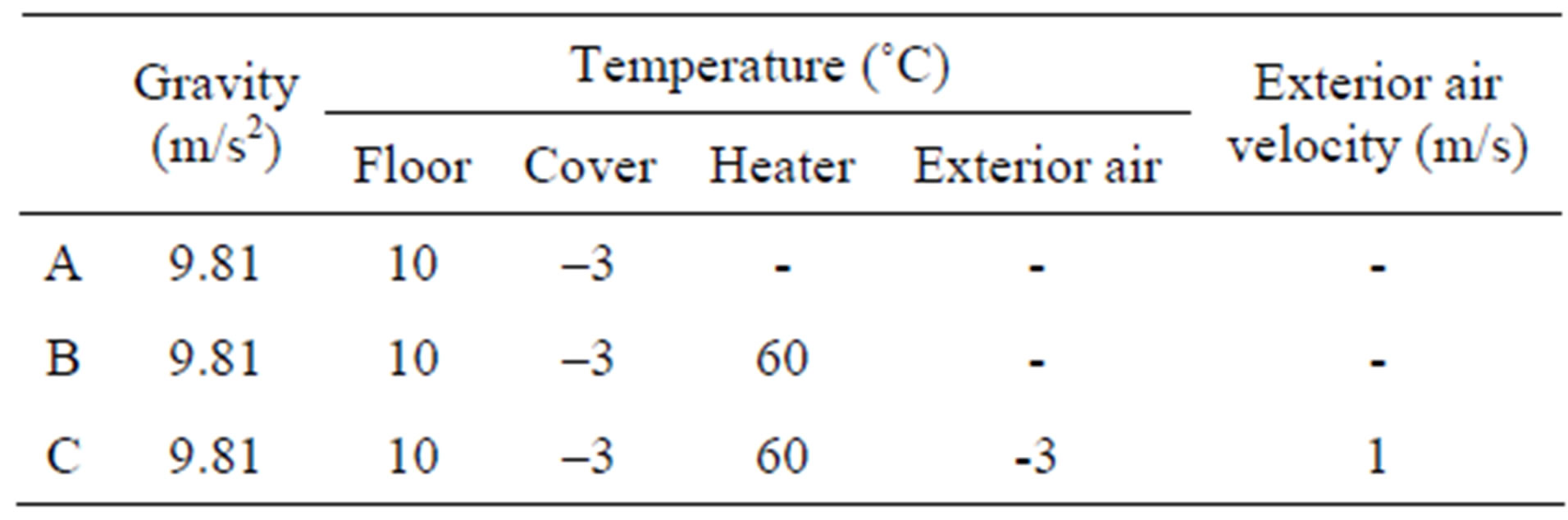
Table 2. Boundary conditions.

Table 3. Convergence of our solution (CM values).
After initial variations, convergence monitors decrease as the analysis approaches convergence, and the number of iterations depends on several factors, such as:
• Complexity of the geometry;
• Mesh refinement;
• The turbulence level indicated by the Reynolds number.
Table 3 describes, for each case, the number of iterations (Ite), the computational time in hours (C(h)), and the residual for each variables (Vx, Vy, Press, ENKE and ENDS).
A special note should be made, as CPU time is concerned, that convergence took a relative long time to reach an acceptable solution. This indicates that the mesh is probably too refined or the TDMA solver was not the best choice.
3. Results and Discussion
3.1. Model Validation
In this section, the experimental and numerical results of temperature are compared. As expected, the temperature distribution inside the greenhouse is affected for the three cases: close without heater tube, close with heater tube and open window with heater. The Temperature results are presented in relative form (Tr = T – Tf). Tr is the relative temperature, Tf is the floor temperature without heater (10˚C). The presented Temperature for the case A
(close greenhouse without heater) shows that the ambient temperature ranges from 1.7˚C to 3˚C. The left side of the greenhouse is colder than the right side on about 1.3˚C. This is due to the wind orientation. In fact the wind is directed from right to the left side of the greenhouse. For the case B, where the heater is open and the greenhouse is close, the temperature increase from 8.3˚C to 10.5˚C. For the greenhouse with a heater tube and opening windows a similar airflow pattern was observed as in case B but with higher velocity values and lower temperature. Indeed, the opening windows allow the freeze air entrance with a velocity equal to 1 m/s. In this case, a temperature of the greenhouse fluctuates from 4.9˚C and 7.4˚C.
As shown in Figure 3, the comparison between the experimental data and the numerical results present a very good agreement for all of the cases. As it’s shown, the average error between experimental and numerical results are 0.2˚C. In case B, where the heater is on, the error on the temperature values are higher than in the two other cases.
3.2. Temperature and Velocity Results
Figure 4 shows the temperature and velocity profiles numerically obtained for each case and for the path AB (represented in Figure 1). In this figure, the temperature is more or less constant between heater tubes locations, and the airflow velocity is higher in the middle of the path. The temperature values are higher than presented above, this is due to path location been only 10cm from heat tubes. On the zone where the heater tube is located the temperature value is around 55˚C. The velocity values vary along the path AB between 0.05 m/s to 0.4 m/s. The high values are observed in the middle of the path. This is due to greenhouse geometry and wind orientation.
For the three cases and on the path CD, the temperature
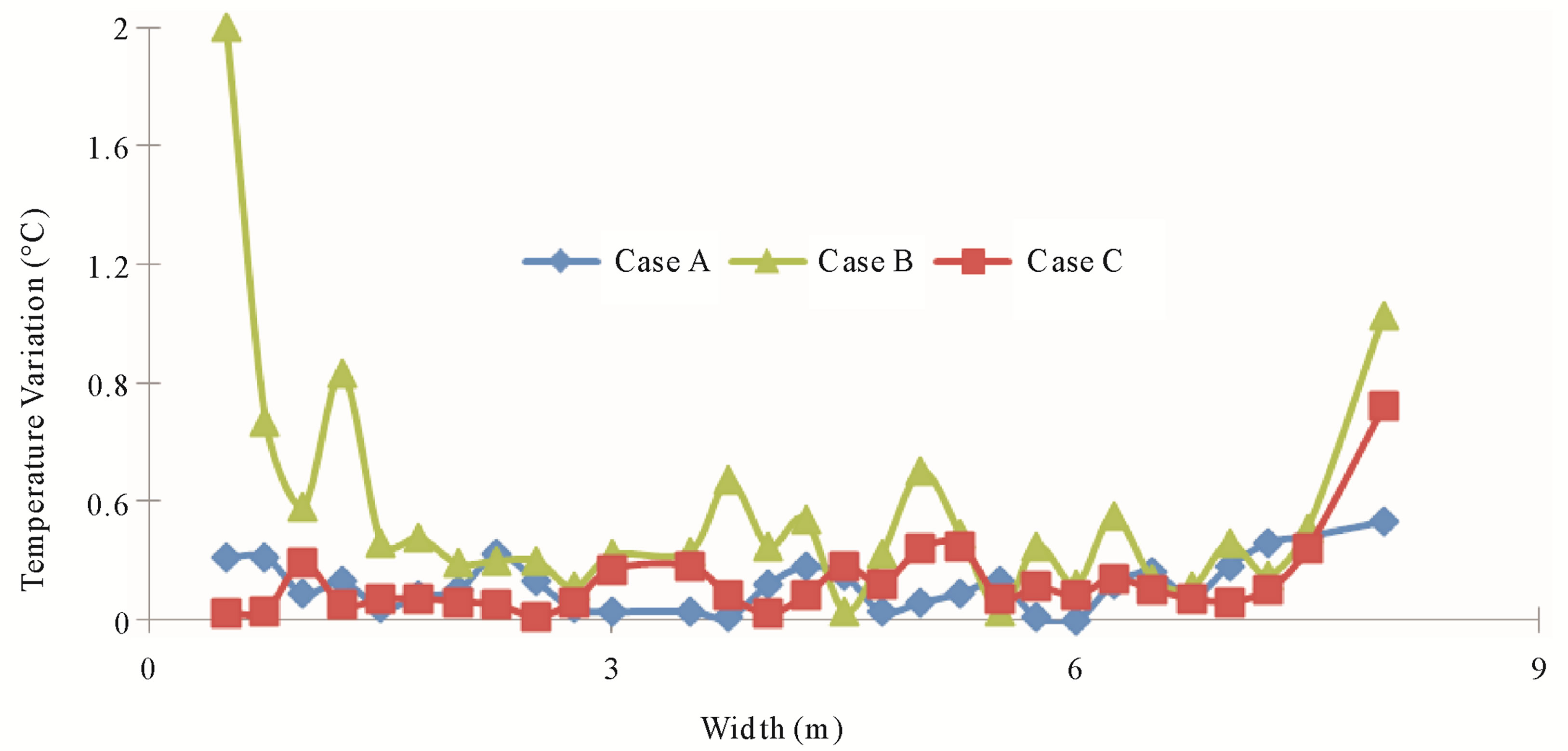
Figure 3. Comparison between experimental and numerical results of temperature for the 3 cases.
and velocity profiles numerically obtained are shown on Figure 5. Is observed that the relative temperature is approximately constant, and the airflow velocity is fluctuate between 0.4 m/s on the left side and 0.1 m/s near the first heater tube location.
The difference in the average temperature value between cases B and C allows verifying that ventilation provokes sufficient energy loss to decrease the temperature in 3˚C. The airflow velocity, in case C is higher than in the other two cases, but only in a certain part of the path. This is due to the fact of the exterior air flow (right to left direction), which feeds the descending convection flow.
In Figure 5 is clearly showed the influence of the AHT and natural ventilation in temperature (about 7˚C in case B and about 3˚C in case C). This influence is almost insignificant in the airflow velocity profile.
As far as temperature is concerned a special note should be made for the thermal inversion that happens in all the vertical paths but is more visible in case B. This behaviour has its cause in the AHT system set at 0.125 m from the soil and the wind orientation.
3.3. Air Velocity inside Greenhouse
In Figures 6-8 the velocity vectors of fluid flow are represented, respectively in situations A, B and C.
The turbulent regime is lower in a greenhouse without heating and no ventilation. Figure 6 shows a main convection flow in anti-clockwise.
The polyethylene heating tubes change substantially the turbulent regime inside the greenhouse.
In this situation, behind the main convection flow, it is possible to identify six other flows generated by the heating tubes.
The turbulent regime increases even further in the situation in which there is air flux between exterior and interior areas. In this situation it is possible to identify secondary convection flows. Another important observation is the fact that, the descending cold airflow velocity is greater than in the situations without air exchange with the exterior, caused by the addition of cold exterior air.
4. Conclusions
In the literature, many researchers are working on the analysis of the wind effect on ventilation [3-5,12], but no work has been done on the wind effect for the greenhouse with AHT implanted in the soil. The influence of AHT in the temperature and air velocity was examined numerically. Three cases were studied, the closed greenhouse without heater tubes, the heater tubes implanted in
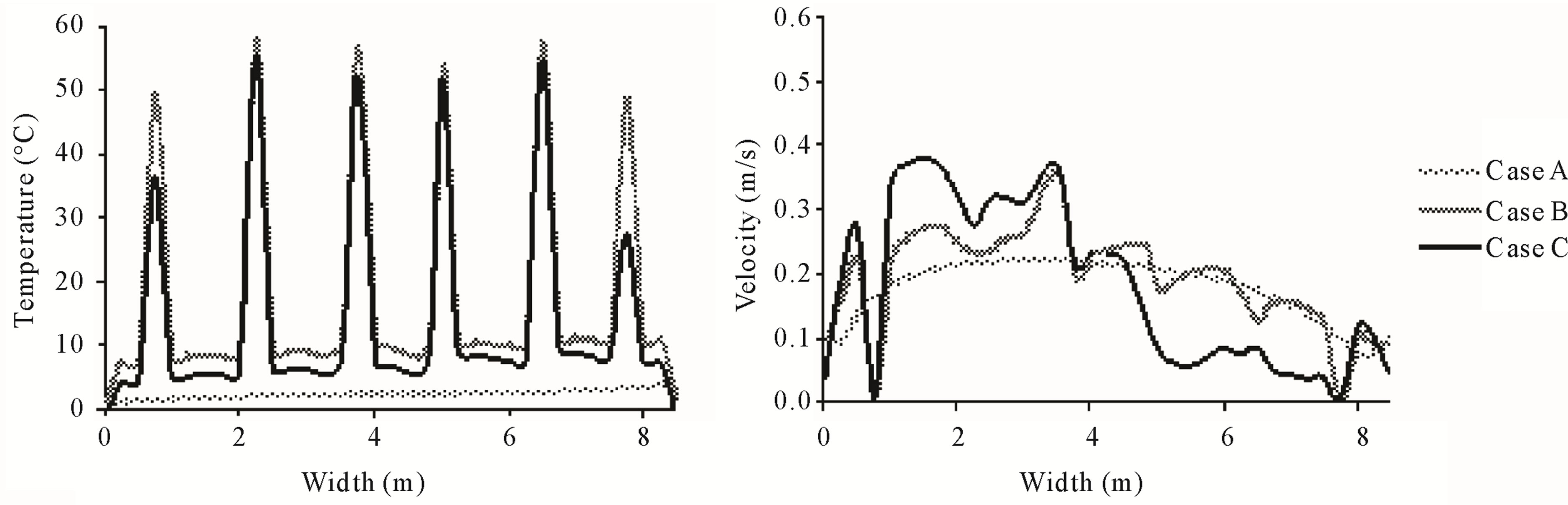
Figure 4. Temperature and velocity profiles on path AB.
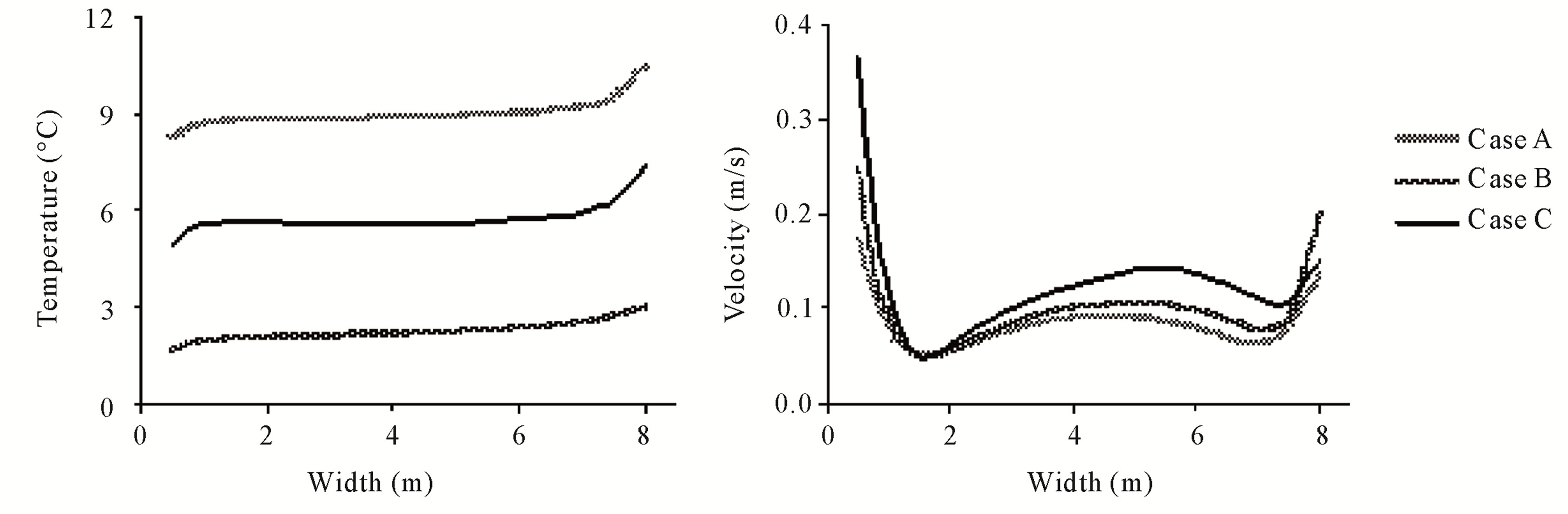
Figure 5. Temperature and velocity profiles on path CD.

Figure 6. Vector of velocity for case A using FLOTRAN.

Figure 7. Vector of velocity for case B using FLOTRAN.

Figure 8. Vector of velocity for case C using FLOTRAN.
the soil in closed greenhouse and finally, the second case with opening windows. Temperatures obtained numerically were compared with experimental data. These demonstrate a good concordance and allow to validate the used numerical code to simulate heat and mass transfer in this studied domain. Then temperatures distribution in a horizontal plane situated 1.125 m from the ground are presented. For each case, the distribution of temperature inside the greenhouse was quite different and the resultant temperature profile was mainly affected by airflow. When the wind enters with a velocity equal to 1 m/s and a temperature equal to 1˚C, the temperature inside the greenhouse decrease significantly (from 19˚C to 16˚C). This decrease depends deeply not only on the wind velocity and its temperature but also on its direction, as studied.
Air velocity distribution along the greenhouse presents a main circulation in the middle of the greenhouse for all situations. In respect to the openings, both air velocity and temperature had a uniform distribution along the greenhouse and air velocity varied between 0.3 and 0.4 m/s. When air flow was parallel to the openings and each opening acted as an inlet and an outlet, we observed regions inside the greenhouse, mainly in the middle of greenhouse, with very low air velocities (0.05 - 0.1 m/s). Consequently, temperature gradually increased between the two openings up to 5˚C higher than the outside air.
This paper describes and evaluates the computational facilities using the finite element method to study the effects of heating tubes and natural ventilation on greenhouses indoor air properties especially during the night.
In opposite to earlier works, usually based on thermal loads, in this study the incompressible Reynolds averaged Navier-Stokes equations with the k-e model was performed. This numerical procedure avoids the use of empirical heat transfer coefficients and provides adequate CPU (Computational Processing Unit) time and residual values. This mathematical model was implemented in FLOTRAN module of ANSYSâ, which is based on finite element method. Good agreement has been observed between the numerical and experimental values. This allows to validate the Computational Fluid Dynamics code used in this work.
Results shown that the heating tubes increases the temperature in about 6.7˚C. If both heating tubes and natural ventilation are introduced this increase reduces to about 3.5˚C. Turbulent regime is lower in case A, and it increases slightly when the heating system is introduced (case B), and it increases significantly in case C due to the effect of natural ventilation.
The simulation of these processes using ANSYS can be a good path to explore, namely in the simulation of three dimension resolution and optimizing the size of the element mesh in order to reduce the computation time.
REFERENCES
- I. Seginer, “Optimal Control of the Greenhouse Environment: An Overview,” Acta Horticulturae, Vol. 406, 1996 pp. 191-201.
- O. Korner and H. Chala, “Design for Improved Temperature Integration Concept in Greenhouse Cultivation,” Computers and Electronics in Agriculture, Vol. 39, No. 1, 2003, pp. 39-59. doi:10.1016/S0168-1699(03)00006-1
- T. Boulard and B. Draoui, “Calibration and Validation of a Greenhouse Climate Control Model,” Acta Horticulturae, Vol. 406, 1996, pp. 49-61.
- B. J. Bailey and W. Day, “The Use of Models in Greenhouse Environmental Control,” Acta Horticulturae, Vol. 491, 1999, pp. 93-99.
- T. Boulard and S. Wang, “Experimental and Numerical Studies on the Heterogeneity of Crop Transpiration in a Plastic Tunnel,” Computers and Electronics in Agriculture, Vol. 34, No. 1-3, 2002, pp. 173-190. doi:10.1016/S0168-1699(01)00186-7
- S. Wang and T. Boulard, “Measurement and Modelling of Radioactive Heterogeneity in a Greenhouse Tunnel,” Acta Horticulturae, Vol. 534, 2000, pp. 139-146.
- S. Wang and J. Deltour, “Theoritical Study of Natural Ventilation Flux in a Single Span Greenhouse,” Biotechnologie, Agronomie, Société et Environnement, Vol. 2, No. 4, 1998, pp. 256-263.
- S. Wang, J. Pieters and J. Deltour “Studies on Radiometric, Thermal and Climatic Properties of a New Greenhouse Covering Materials,” Acta Horticulturae, Vol. 491, 1998, pp. 324-333.
- J. J. Costa, L. A. Oliveira and D. Blay, “Test of Several Versions for the K-E Type Turbulence Modelling of Internal Mixed Convection Flows,” International Journal of Heat and Mass Transfer, Vol. 42, No. 23, 1999, pp. 4391- 4409. doi:10.1016/S0017-9310(99)00075-7
- J. H. Ferziger and M. Perić, “Computational Methods for Fluid Dynamics,” 2nd Edition, Springer Verlag, New York, 1999. doi:10.1007/978-3-642-98037-4
- J. C. Tannehill, D. A. Anderson and R. H. Pletcher, “Computational Fluid Mechanics and Heat Transfer,” 2nd Edition, Taylor & Francis Ltd., Oxfordshire, 1997.
- B. J. Bailey, “Optimal Control of Dioxide Enrichment in Ventilated Greenhouses. Workshop on Management,” Identification and Control of Agriculture Buildings, Universidade de Trás-os-Montes e Alto Douro, Vila Real, 1998, pp. 1-15.

