World Journal of Mechanics
Vol. 1 No. 2 (2011) , Article ID: 4668 , 6 pages DOI:10.4236/wjm.2011.12003
Visco-Elastic Boundary Layer Flow past a Stretching Plate and Heat Transfer with Variable Thermal Conductivity
Department of Mathematics, Jamia Millia Islamia, New Delhi, India
E-mail: naseem_mt@yahoo.com
Received February 11, 2011; revised March 6, 2011; accepted March 11, 2011
Keywords: Boundary Layer Flow, Similarity Solution, Variable Thermal Conductivity, Prandtl Number
ABSTRACT
In the present paper, the boundary layer flow of Walters Liquid B Model over a stretching plate has been considered to solve heat flow problem with variable conductivity. First, using similarity transformation, the velocity components have been obtained. Then, the heat flow problem has been considered in two ways: 1) prescribed surface temperature (PST), and 2) prescribed stretching plate heat flux (PHF) in case of variable conductivity. Due to variable conductivity, temperature profile has its two partone mean temperature and other temperature profile induced due to variable conductivity. The related results have been discussed with the help of graphs.
1. Introduction
Due to number of applications in industrial manufacturing process, the problem of boundary layer flow past a stretching plate has attracted considerable attention of researchers during the past few decades. Examples of such technological process are hot rolling, wire drawing, glassfiber and paper production. In the process of drawing artificial fibers the polymer solution emerges from orifice with a speed which increases from almost zero at the orifice up to a plateau value at which it remains constant. The moving fiber, which is of great technical importance, is governed by the rate at which the fiber is cooled and this, in turn affects the final properties of the yarn. A number of works are presently available that follow the pioneering classical work of Sakiadis [1], F. K. Tsou, E. M. Sparrow, R. J. Goldstein [2] and Crane [3]. The following Table lists some relevant works that pertain to cooling liquids, i.e., heat transfer for stretching surface:


There are liquid metals whose thermal conductivity varies with temperature in an approximately linear manner in the range from 0˚ F to 400˚ F. In 1996, T. C. Chiam [22] considered heat transfer problem with variable thermal conductivity in stagnation-point flow towards stretching sheet. N. Ahmad and K. Marwah [16,17] also studied boundary layer flow of Walters Liquid B Model with heat transfer for linear stretching plate with variable thermal conductivity numerically.
In almost all the flow problems over stretching sheet with heat transfer referred so far where closed form solution is obtained, the thermal conductivity of liquid has been taken constant. In this paper, we try to solve the boundary layer flow of Walters Liquid B Model over a stretching plate and heat transfer with variable thermal conductivity in the following two cases:
1) prescribed surface temperature (PST), and 2) prescribed stretching plate heat flux (PHF). The temperature field has been obtained in each case and the effect on it, of Visco-elasticity and Prandtl number has been discussed graphically.
2. Mathematical Formation and Solution
The problem considered here is the steady boundary layer flow due to a moving flat plate in a quiescent Walters Liquid B Model. The flow is two dimensional where x-axis is along the plane of moving plate and y-axis is normal to it, respectively. We assume that the surface is moving continuously with the velocity 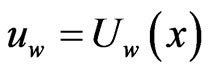 in the positive x-direction. Under these assumptions, the boundary layer along moving plate is governed by the equations:
in the positive x-direction. Under these assumptions, the boundary layer along moving plate is governed by the equations:
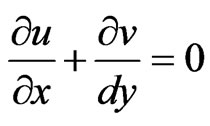 (1)
(1)
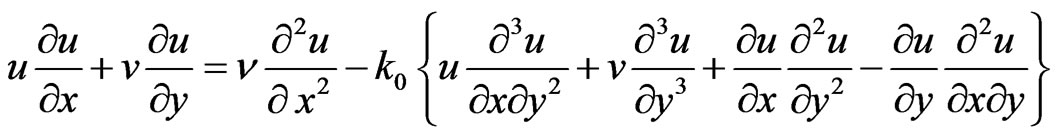 (2)
(2)
where u, the horizontal velocity component; v, the vertical velocity component;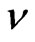 , the kinematic viscosity; k0, the coefficient of visco-elasticity The relevant boundary conditions are:
, the kinematic viscosity; k0, the coefficient of visco-elasticity The relevant boundary conditions are:

Introducing the dimensionless variables
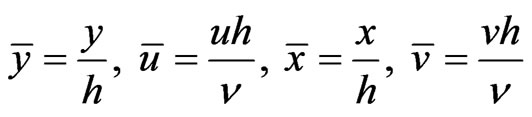
the Equations (1) and (2) reduce to
 (3)
(3)
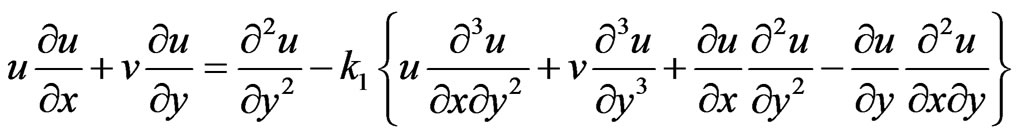 (4)
(4)
where k1=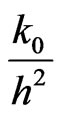 with boundary conditions
with boundary conditions
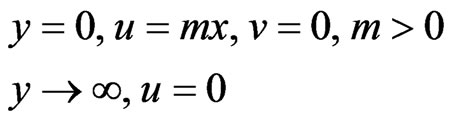 (5)
(5)
where bar has been dropped for convenience.
Setting the similarity solution of the form , we have
, we have
 (6)
(6)
Putting u and v in the Equation (2), we have
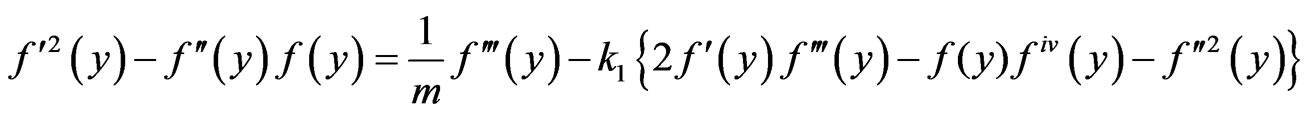 (7)
(7)
which is non-linear differential equation of order three.
The boundary conditions (5) reduce to
 (8)
(8)
 (9)
(9)
Boundary conditions suggest that the velocity function may be of the form 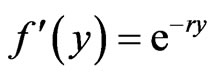 where r is complex number with positive real part. Thus,
where r is complex number with positive real part. Thus,
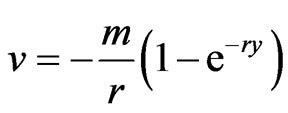
Now, from the Equation (7), we get .
.
Therefore, the velocity components become as follows:
 (8)
(8)
3. Heat Transfer Problem
In absence of viscous dissipation and heat generation, the energy equation for two dimensional heat flow is given by
 (9)
(9)
subject to boundary conditions
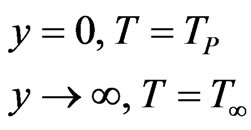 (10)
(10)
where TP is plate temperature, T¥ is temperature of surrounding fluid, CP is specific heat at constant pressure and k is thermal conductivity.
3.1. Case A: Prescribed Power Law Surface Temperature (PST)
Let the surface temperature be of the form
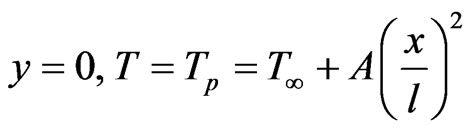
while the temperature out side the dynamic region be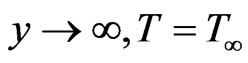 . Now, we define the dimensionless temperature by
. Now, we define the dimensionless temperature by
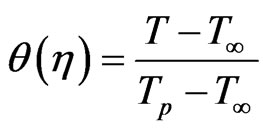
where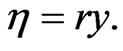 .
.
For liquid metals, it has been found that the thermal conductivity varies with temperature in an approximately linear manner in the range from 0˚ F to 400˚ F. Therefore, we assume k as 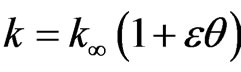 where
where .
.
Now, substituting u and v and changing the independent variable y to , we have
, we have
 (11)
(11)
with boundary conditions
 (12)
(12)
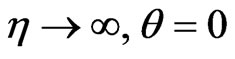 (13)
(13)
From Equation (11), we note that the heat transfer takes place in two parts, that is, one part of heat transfer is due to temperature difference and the other part is due to variable thermal conductivity. We denote the first part by qm and second by qv. Thus, equating the terms independent of e and the terms involving e, we have
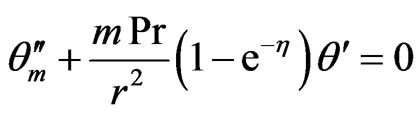 (14)
(14)
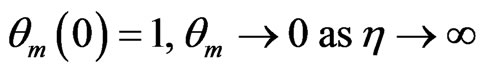 (15)
(15)
and
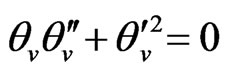 (16)
(16)
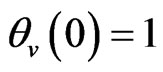 ,
, 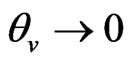 as
as 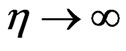 (17)
(17)
The solution of the Equation (14) is
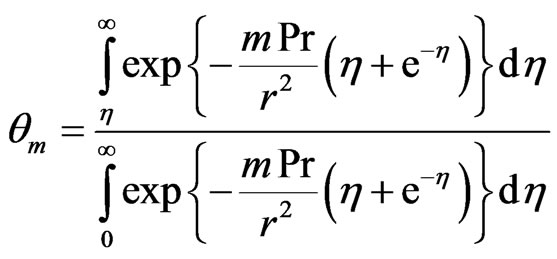 (18)
(18)
Equation (17) is a non-linear differential equation of order two. Let the solution of this equation be of the form

Putting this solution in the Equation (18), we have
 (19)
(19)
The roots of this equation are 0 and 1/2. Therefore,
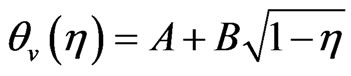 (20)
(20)
The general solution (20) of the Equation (16) is real only when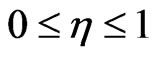 . Therefore, the heat transfer due to variable thermal conductively takes place within the dynamic region
. Therefore, the heat transfer due to variable thermal conductively takes place within the dynamic region . Hence, the boundary conditions (17) may be presented as
. Hence, the boundary conditions (17) may be presented as
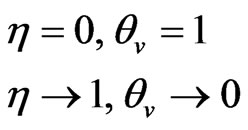 (21)
(21)
The solution (20) finally reduces to
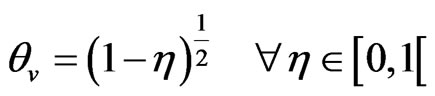 (22)
(22)
3.2. Case B: Prescribed Power Law Surface Heat Flux (PHF Case)
The power law heat flux on the surface of stretching plate is considered to be a quadratic power of x in the form
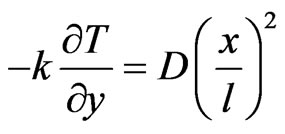 at
at  (23)
(23)
 , as
, as  (24)
(24)
where D is a constant, k is the thermal conductivity. Now we define dimensionless temperature  by
by
 (25)
(25)
where
 when
when 
and .
.
Writing the Equation (11) in terms of , we get the following differential equation
, we get the following differential equation
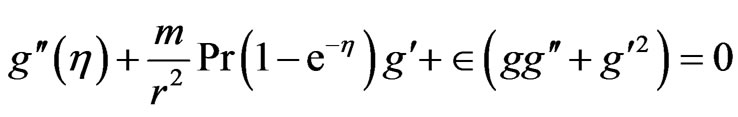 (26)
(26)
together with boundary conditions:
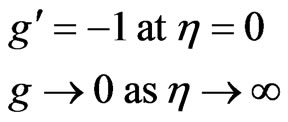 (27)
(27)
Equating the terms independent of  and the terms involving
and the terms involving  from Equation (26), we get the following two boundary value problems:
from Equation (26), we get the following two boundary value problems:
 (28a)
(28a)
 ,
,  as
as  (28b)
(28b)
and,
 (29a)
(29a)
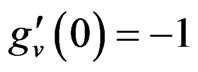 ,
,  as
as  (29b)
(29b)
The solution of the Equation (28a) together with boundary conditions (28b) is given by
 (30)
(30)
The general solution of the Equation (29a) is
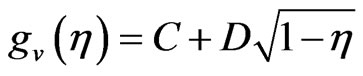 (31)
(31)
where C and D are arbitrary constants to be determined. Here, we observe that the dynamic region for this temperature field is  as it was in PST case. Therefore, the boundary conditions may be taken as
as it was in PST case. Therefore, the boundary conditions may be taken as
 (32)
(32)
Hence finally the solution becomes
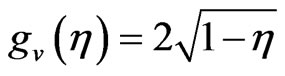 (32)
(32)
4. Discussion and Results
A boundary layer flow of visco-elastic fluid (Walters Liquid B Model) over a stretching plate and heat transfer has been analyzed through out this paper. The boundary layer equations of momentum and heat transfer have been solved analytically. Two different analytical expressions have been obtained for dimensionless temperature fields for two general cases of boundary conditions namely 1) PST case, and 2) PHF respectively. The equation governing the induced temperature field due to variable thermal conductivity has been solved with modified boundary conditions in both the cases PST and PHF The related results have been discussed in the subsequent paragraphs in detail.
Figure 1 is a graph drawn for mean temperature field  versus
versus 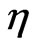 in PST case taking different values of visco-elastic parameter
in PST case taking different values of visco-elastic parameter . It is observed that the temperature
. It is observed that the temperature 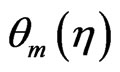 at the surface of stretching plate is invariant with respect to physical parameters. Further, we observe that as we move away the stretching plate within dynamic region, the temperature field increases as viscoelastic parameter
at the surface of stretching plate is invariant with respect to physical parameters. Further, we observe that as we move away the stretching plate within dynamic region, the temperature field increases as viscoelastic parameter  increases. Physically, when
increases. Physically, when 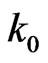 increases, the fluid absorbs more heat which causes the increase of temperature.
increases, the fluid absorbs more heat which causes the increase of temperature.
Figure 2 exhibits variation pattern of mean temperature field qm(h) with regard to Prandtl number Pr in PST case. We notice that as Prandtl number Pr increases, the mean temperature decreases.
Figure 3 exhibits the variation pattern of induced temperature field qv in PST case. This temperature field is independent of k0 and Pr. We see that the induced temperature decreases as we move away the plate. The variation pattern is represented by a parabolic curve having focus at h = 1. qv decreases as we move away the stretching plate and it becomes almost zero at h = 1 which end upper edge of boundary layer thickness.
Figure 4 is the graph of mean temperature field  versus
versus  in PHF case. Here we observe that this temperature field attains the maximum value at the surface of stretching plate which is more than PST case. The reason of this maximum value is that the direction of heat flow is from fluid to stretching plate. Temperature field is approaching to zero asymptotically. The variation pattern is almost same as in PST case.
in PHF case. Here we observe that this temperature field attains the maximum value at the surface of stretching plate which is more than PST case. The reason of this maximum value is that the direction of heat flow is from fluid to stretching plate. Temperature field is approaching to zero asymptotically. The variation pattern is almost same as in PST case.
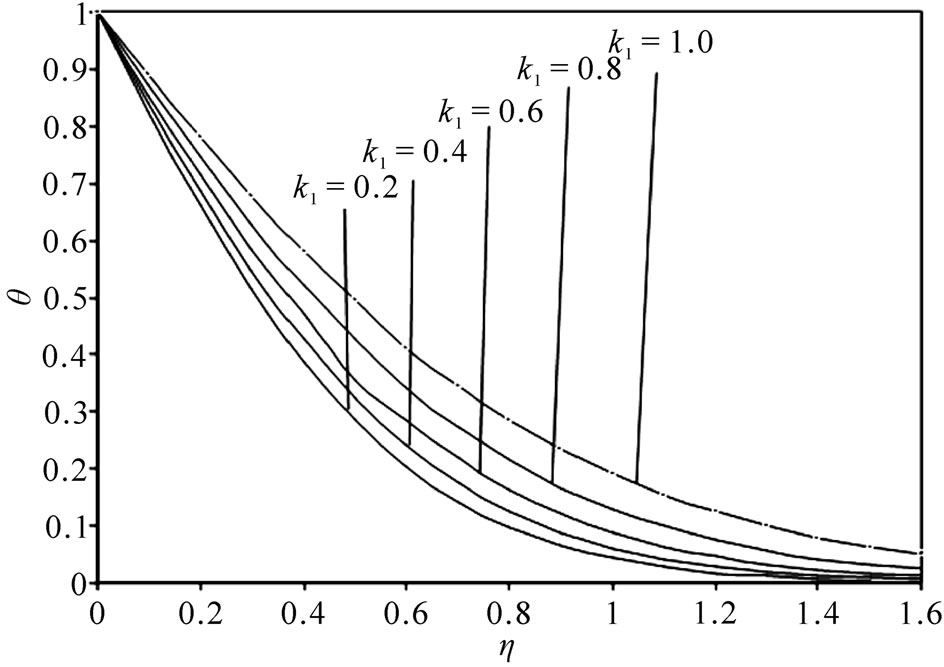
Figure 1. Mean temperature θm(η) for different values of visco-elastic parameter k1 in PST case.
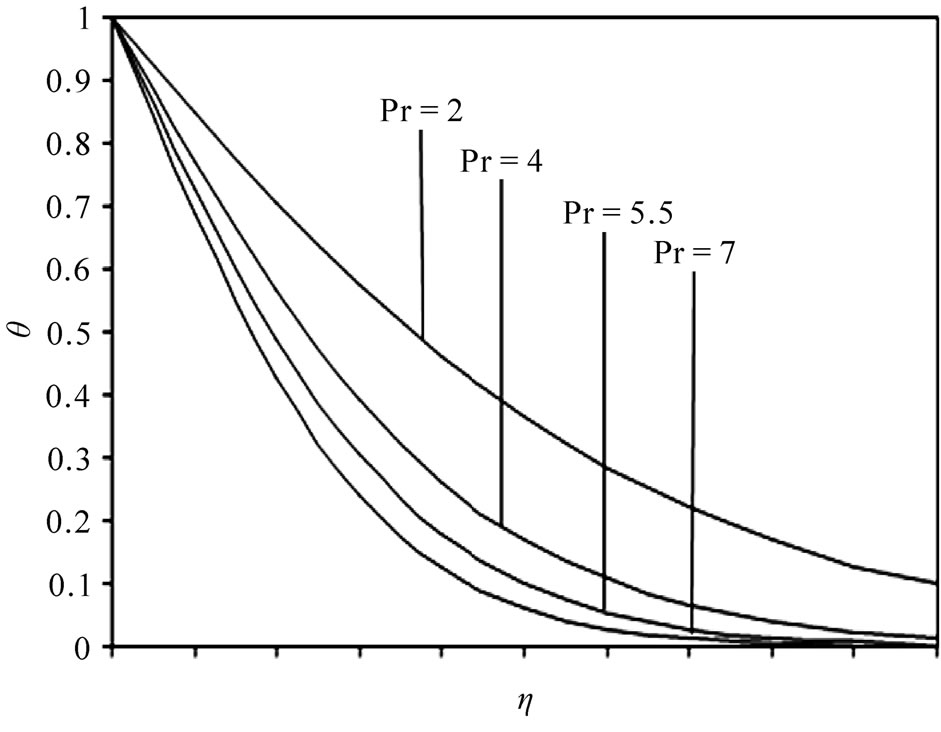
Figure 2. Effect of Prandtl number Pr mean temperature field θm(η) keeping visco-elasticity k1 = 0.4 fixed in PST case.

Figure 3. Variation pattern of θv within dynamic region [0,1) PST case.

Figure 4. Mean temperature gm(η) for different values of visco-elastic parameter k1 in PHF case.
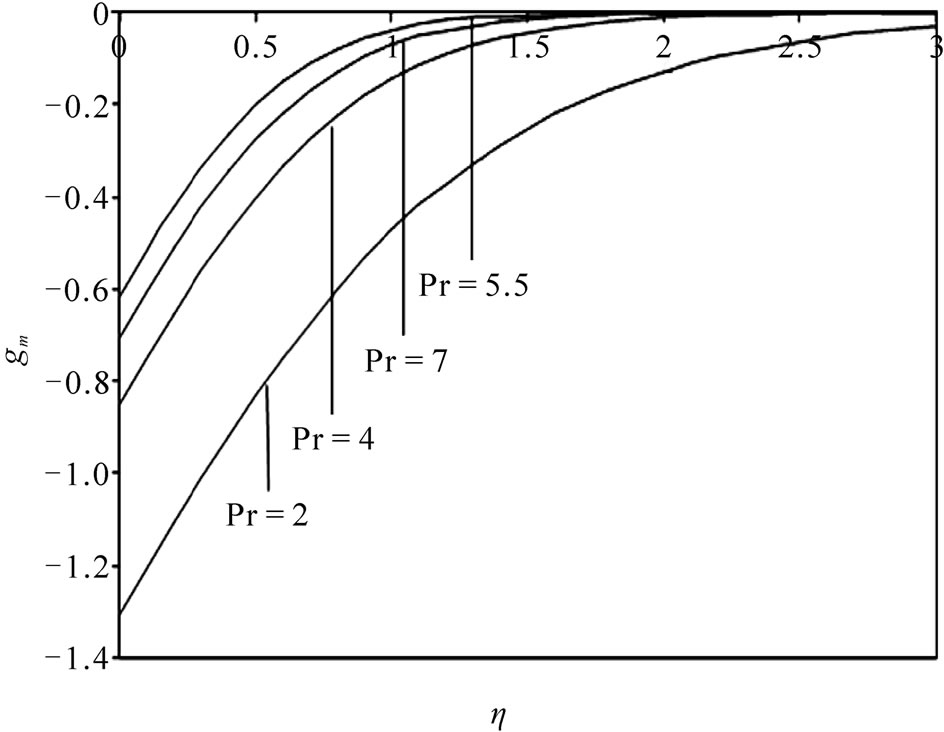
Figure 5. variation pattern of mean temperature gm(η) for different values of Prandtl number Pr for k1= 0.4 in PHF case.
Figure 5 shows the graph of  versus
versus  for the different values of Prandtl number Pr in PHF case. It has been observed that as Pr increases, temperature field decreases absolutely. Temperature field is tending to zero asymptotically.
for the different values of Prandtl number Pr in PHF case. It has been observed that as Pr increases, temperature field decreases absolutely. Temperature field is tending to zero asymptotically.
Equation (32) represents the temperature field induced by variable thermal conductivity in PHF case. The geometry of this equation is parabola having focus at h = 1. This temperature field is independent of k1 and Pr. We see that the induced temperature decreases as we move away the plate. It varies from maximum at the plate to zero at the upper end of boundary layer.
Putting k0 = 0, we get the results due to Naseem Ahmad, Z. U. Siddiqui and M. K. Mishra [23].
5. Conclusion
The boundary layer flow of Walters Liquid B over linear stretching plate has been studied together with heat transfer with variable thermal conductivity. The heat transfer has been studied by considering two cases: PST and PHS. The effect of visco-elasticity k0 has been looked upon in the Figures 1 and 2. This paper is an extension of the work due to Naseem Ahmad, Z. U. Siddiqui and M. K. Mishra [23].
REFERENCES
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: II Boundary Layer on a Continuous Flat Surface,” AIChE Journal, Vol. 7, No. 2, 1961, pp. 221- 225. doi:10.1002/aic.690070211
- F. K. Tsou, E. M. Sparrow and R. J. Goldstein, “Flow and Heat Transfer in the Boundary Layer on a Continuous Moving Surfaces,” International Journal of Heat and Mass Transfer, Vol. 10, No. 2, February 1967, pp. 219- 235. doi:10.1016/0017-9310(67)90100-7
- L. J. Crane, “Flow Past a Stretching Plate,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- K. R. Rajagopal, T. Y. Na and A. S. Gupta, “Flow of a Visco-Elastic Fluid over a Stretching Sheet,” Rheologica Acta, Vol. 23, No. 2, 1984, pp. 213-215.
- K. R. Rajagopal, T. Y. Na and A. S. Gupta, “A Non Similar Boundary Layer on a Stretching Sheet in a NonNewtonian Fluid with Uniform Free Stream,” Journal of Mathematical and Physical Sciences, Vol. 21, No. 2, 1987, pp. 189-200.
- N. M Bujurke, S. N. Biradar and P. S. Hiremath, “Second Order Fluid Flow Past a Stretching Sheet with Heat Transfer,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 38, No. 4, 1987, pp. 890-892. doi:10.1007/BF00946345
- B. S. Dhanpat and A. S. Gupta, “Flow and Heat Transfer in a Viscoelastic Fluid over a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 24, No. 3, 1989, pp. 215-219.
- N. Ahmad, G. S. Patel and B. Siddappa, “Visco-Elastic Boundary Layer Flow Past a Stretching Plate and Heat Transfer,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 41, No. 2, 1990, pp. 294-298. doi:10.1007/BF00945114
- D. Rollins and K. Vajravelu, “Heat Transfer in a Second Order Fluid over a Continuous Stretching Surface,” Acta mechanica, Vol. 89, No. 1-4, 1991, pp. 167-178. doi:10.1007/BF01171253
- N. Ahmad, G. S. Patel and B. Siddappa, “Viscoelastic Boundary Layer Flow Past a Stretching Plate with Suction and Heat Transfer,” Jnanabh, Vol. 21, 1991, pp. 47- 58.
- S. P. Lawrence and N. B. Rao, “Heat Transfer in the Flow of a Viscoelastic Fluid over a Stretching Sheet,” Acta Mechanica, Vol. 93, No. 1-4, 1992, pp. 53-61. doi:10.1007/BF01182572
- M. I. Char, “Heat and Mass Transfer in a Hydromagnetic Flow of Viscoelastic Fluid over a Streatching Sheet,” Journal of Mathematical Analysis and Applications, Vol. 186, No. 3, 1994, pp. 674-689. doi:10.1006/jmaa.1994.1326
- A. Naseem, “On Temperature Distribution in a No-Participating Medium with Radiation Boundary Condition,” International Journal of Heat and Technology, Vol. 14, No. 1, 1995, pp. 19-28.
- N. Ahmad, “The Stretching Plate with Suction in NonParticipating Medium with Radiation Boundary Condition,” International Journal of Heat and Technology, Vol. 14, No. 1, 1996, pp. 59-66.
- D. Kelly, K. Vjravelu and L. Andrews, “Analysis of Heat Mass Transfer of a Visco-Elastic, Electrically Conducting Fluid Past a Continuous Stretching Sheet,” Nonlinear Analysis, Vol. 36, No. 6, June 1999, pp. 767-784. doi:10.1016/S0362-546X(98)00128-X
- N. Ahmad and K. Marwah, “Visco-Elastic Boundary Layer Flow Past a Stretching Plate and Heat Transfer with Variable Conductivity,” Proceedings of 44th Congress ISTAM, 1999, pp. 60-68.
- N. Ahmad and K. Marwah, “Viscoelastic Boundary Layer Flow Past a Stretching Plate with Suction and Heat Transfer with Variable Conductivity,” Indian Journal of Engineering and Material Sciences (IJMS), Vol. 7, 2000, pp. 54-56.
- A. M. Subhas, A. Joshi and R. M. Sonth, “Heat Transfer in MHD Viscoelastic Fluid Flow over a Stretching Surface,” Zeitschrift für Angewandte Mathematik und Mechanik (ZAMM), Vol. 81, No. 10, 2001, pp. 691-698. doi:10.1002/1521-4001(200110)81:10<691::AID-ZAMM691>3.0.CO;2-Z
- R. M. Sonth, S. K. Khan, A. M. Subhas and K. V. Prasad, “Heat and Mass Transfer in a Viscoelastic Fluid Flow over an Accelerating Surface with Heat Source/Sink and Viscous Dissipation,” International Journal of Heat and Mass Transfer, Vol. 38, No. 3, 2002, pp. 213-220. doi:10.1007/s002310100271
- P. G. Siddheshwar and U. S. Mahabaleswar, “Effects of Radiation and Heat Source on MHD Flow of Viscoelastic Liquid and Heat Transfer over Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 40, No. 6, July 2005, pp. 807-821. doi:10.1016/j.ijnonlinmec.2004.04.006
- T. C. Chiam, “Heat Transfer with Variable Conductivity in Stagnation-Point Flow towards a Stretching Sheet,” International Communications in Heat and Mass Transfer, Vol. 23, No. 2, 1996, pp. 239-248. doi:10.1016/0735-1933(96)00009-7
- M. S. Abel, P. G. Siddheshwar and M. M. Nandeppanavar, “Heat Transfer in a Viscoelastic Boundary Layer Flow over a Stretching Sheet with Viscous Dissipation and Non-Uniform Heat Source,” International Journal of Heat and Mass Transfer, Vol. 50, No. 5-6, March 2007, pp. 960-966.
- N. Ahmad, Z. U. Siddiqui and M. K. Mishra, “Boundary Layer Flow and Heat Transfer Past a Stretching Plate with Variable Thermal Conductivity,” International Journal of Non-Linear Mechanics, Vol. 45, No. 3, April 2010, pp. 306-309. doi:10.1016/j.ijnonlinmec.2009.12.006

