World Journal of Condensed Matter Physics
Vol.08 No.01(2018), Article ID:82035,22 pages
10.4236/wjcmp.2018.81001
Violation of Cluster Property in Quantum Antiferromagnet
Tomo Munehisa
Faculty of Engineering, University of Yamanashi, Kofu, Japan
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 8, 2017; Accepted: January 23, 2018; Published: January 26, 2018
ABSTRACT
The cluster property is one of fundamental properties in physics. This property means that there are no relations between two events that are sufficiently separated. Because the cluster property is directly connected with entanglement in quantum field theory and in many-body systems, theoretical and experimental progress on entanglement stimulates us to study this property deeply. In this paper we investigate the cluster property in the spin 1/2 XXZ antiferromagnet on the square lattice with an explicitly symmetry breaking interaction of strength g. In this model spontaneous symmetry breaking occurs when the lattice size N is infinitely large. On the other hand, we have to make g zero in order to obtain quantities in the XXZ model with no symmetry breaking interaction. Since some results depend on the sequence of limit operations ― and , it is difficult to draw a clear conclusion in these limits. Therefore we study the model with finite g on the finite lattice, whose size N is supposed to be 1020, for our quantitative calculations. Then we can obtain the concrete ground state. In order to study the cluster property we calculate the spin correlation function. It is known that the function due to Nambu-Goldstone mode (gapless mode), which is calculated using linear spin wave theory, satisfies this property. In this paper we show that almost degenerate states also induce the spin correlation. We assume that the spin correlation function in measurements is a sum of the function due to Nambu-Goldstone mode and one due to these degenerate states. Then we examine whether the additional correlation function violates the cluster property or not. Our conclusion is that this function is finite at any distance, which means the violation of the cluster property, and it is of order of . Except for the case of extremely small g, this violation is the fine effect. Therefore the correlation function due to the degenerate states can be observed only when it is larger than the spin correlation function due to Nambu-Goldstone mode. We show that g required for this condition depends on the distance between positions of two spin operators.
Keywords:
Cluster Property, Entanglement, Quantum Antiferromagnet, Spontaneous Symmetry Breaking

1. Introduction
It has been widely understood that entanglement is one of the fundamental concepts in quantum physics. In entanglement the particle correlation is contradictory to the classical concept on the locality [1] . Entanglement between a few particles has been extensively studied first in order to establish strict foundation of quantum mechanics. Although this study belongs to the basic science, it became well-known that entanglement can be applied to quantum information or quantum computer [2] . By these applications we find a huge number of papers on entanglement [3] [4] [5] . Recently the concept of entanglement has spread over other fields such as particle physics [6] [7] [8] .
Another fundamental concept in quantum physics is spontaneous symmetry breaking (SSB) [9] [10] . We find extensive studies about relations between entanglement and SSB in many-body systems [11] . One target of these studies is to measure entanglement in experiments [11] [12] . Another target is to clarify the above relation in terms of the classical order [13] [14] [15] . But concrete calculations about entanglement have been limited to simple models such as boson systems with no interactions [15] or one-dimensional ferromagnet [16] .
The entangled particles are correlated even when the particles are separated from each other. If the distance between two particles is infinitely large, the entangled correlation implies the violation of the cluster decomposition [10] or the cluster property [17] .
Physical meaning of the cluster property, which is the most basic principle in physics [10] , is that there is no relation between two events that occur when the distance between these events is infinitely large. Let us give more accurate definition for the cluster property in quantum field theory [17] . Introducing a local operator at a position and another local operator at a position , we calculate the expectation values of these operators in the ground state ,
(1)
Then we calculate the expectation value of the product of these operators,
(2)
When the distance between positions and is very large, we expect that the above correlation function agrees with the product of and ,
(3)
If the Equation (3) holds, the correlation function satisfies the cluster property. If it does not hold, then the cluster property fails.
When we assume that the ground state is only one state that satisfies the translational invariance, the cluster property is guaranteed in quantum field theory. But this assumption is not trivial in SSB because the ground state consists of the degenerate states. It has been also pointed out that the violation of this property is deeply connected with confinement in QCD [18] [19] , because we cannot separate the quark operator far from the anti-quark operator. With these interests there are active studies on the cluster property in quantum field theory [20] [21] .
In the many-body systems, on the other hand, we find only a few studies on the cluster property. Authors in works [22] [23] clarified the relation between the stability of the macroscopic system and the cluster property. In these papers it was pointed out that the ground state of the coherent state satisfies the cluster property, while the ground state of the number-fixed state does not. However, they cannot determine the ground state uniquely by Hamiltonian, so that they did not clarify what is the condition under which the cluster property is valid. Also in [17] it was shown that the cluster property fails in the Ising quantum spin model on the chain with a free boundary condition, although it holds with other boundary conditions. It should be noted that the lecture of [17] does not include discussion on the property in systems having the continuous symmetry.
In this paper we would like to investigate the cluster property of the quantum antiferromagnet on the two-dimensional lattice. It is well known that the ground states of models on this system realize semi-classical Neel order [24] , in other words, SSB of SU(2) or U(1) symmetry. This realization has been strongly supported by spin wave theory (SWT) [25] as well as numerical studies [26] [27] . Also there are many experimental reports about this order [28] [29] .
For our study we employ the spin 1/2 XXZ antiferromagnet on the square lattice. This model, with U(1) symmetry, is a simplified one of the Heisenberg model which has SU(2) symmetry. We study the model on the lattice whose size N is very large but finite, because the limit operation on N is quite subtle in SSB. One important fact clarified by the previous numerical study [24] is that the eigen energy characterized by the quantum number of U(1) symmetry is almost degenerate. This implies that we have strictly degenerate states when N becomes infinitely large, while we do not have any degenerate states on the finite lattice. Therefore one should not make a simple operation on this limit.
In order to determine the ground state uniquely we introduce an additional interaction that explicitly breaks the symmetry, which forms a disturbance in experiment. Then we quantitatively calculate the spin correlation function using the Hamiltonian with the additional interaction. We suppose that the correlation function is a sum of the correlation function due to the quasi-degenerate states and the one due to Nambu-Goldstone mode.
Contents of this paper are as follows. In the next section we show the property of the ground state in SSB. Here we emphasize that the ground state consists of the lowest energy states with the quantum number n of U(1) symmetry. Also it is stressed that if the ground state has the non-zero expectation value of a local spin operator, this operator connects the state of with the state of n. We will find that the violation of the cluster property originates from this connection. After introducing the concrete model of the spin 1/2 XXZ antiferromagnet on the square lattice with the symmetry breaking interaction in Section 3, we calculate its ground state in Section 4. In our calculations we make a continuous approximation about n, which is valid provided that the size N is large.
In Section 5 we calculate the spin correlation function. In subsection 5.1 we calculate the spin correlation function due to Nambu-Goldstone mode. Here we employ spin wave theory [25] in order to obtain a quantitative effect induced by the symmetry breaking interaction. In subsection 5.2 we calculate the spin correlation function due to the quasi-degenerate states. In section 6 we collect the results of the previous section. Then we present our results of the spin correlation function that is related to the violation of the cluster property in the size . The reason for adopting this value is that the molecular distance is of order of 10−10 m and the length of the macroscopic material is of order of 1 m.
The final section is devoted to summary and discussion. In Appendix A we point out that the violation of the cluster property leads large entanglement in the spin systems. In Appendix B we will show the basis of our assumption that the spin correlation function is the sum of the function due to Nambu-Gold- stone mode and the one due to the quasi-degenerate states.
2. Ground State with Spontaneous Symmetry Breaking
In the spin system on the finite lattice, the spin operator is given only at the discrete coordinates , where , so that it is denoted by . The Hamiltonian is constructed by . i.e. . For the generator we can assume, without loss of generality, that
(4)
Since the Hamiltonian has U(1) symmetry, the generator commutes with the Hamiltonian, namely . Therefore the eigen state of can be the eigen state of at the same time. Then the lowest energy state exists for the quantum number n of ,
(5)
In a case of the spin 1/2 system, .
In the standard antiferromagnet we can insist that the ground state is one eigen state of . Actually is the lowest energy for even N and its eigen state is the ground state. As a result SSB does not occur.
A large amount of theoretical and experimental research, however, strongly supports that SSB occurs in the quantum antiferromagnet [24] . Strictly speaking, SSB is the concept that holds in the limit of the infinitely large N. On the finite lattice, signals for SSB appear in two properties. One is a quasi-degeneracy of the eigen energy . In the antiferromagnet on the two-dimensional lattice we have, with a constant ,
(6)
When N is quite large we have the almost same eigen values for . Also it is needed that that has the same quantum number as that of on the space symmetry.
Another property needed for SSB is an existence of a local spin operator , on which there is a non-zero matrix element between these quasi-degenerate states. Therefore it is required that
(7)
Let us show reasons for (6), which is required if the ground state is not the eigen state of . In this case is constructed by the linear combination of the states ,
(8)
When there is no additional interaction, as mentioned before, the ground state is given by on the finite size system. Therefore we need the interaction that explicitly breaks U(1) symmetry. In order to suppress the effect by to the model, this interaction must be quite small. Even if is small, however, should be the linear combination of . To obtain such , it is required that the differences between energy of and those of are quite small.
The condition (7) is also needed by the definition of SSB, which requires a non-zero value of the expectation of the local field in the ground state ,
(9)
See the textbook of the quantum field theory [10] about the above condition for SSB. Since in the antiferromagnet on the square lattice we have Neel order, we replace the local field by the spin operator . Here is a constant which depends on the site i. Then for SSB we require that
(10)
Consequently we can show an existence of the local operator whose matrix elements between the quasi-degenerated states are finite. From (8) and (10) we obtain
(11)
Then it is necessary that for some . Since the spin operator is the charge of 1 for , we have the non-zero matrix element only for . As a result (7) is necessary.
Summarizing this section, the system has the quasi-degenerate states and non-zero matrix elements of on the lattice of the finite size N, when the system has SSB in the limit of the infinitely large N.
3. Our Model
The model we study in this paper is the spin 1/2 XXZ antiferromagnet on the square lattice with an explicitly symmetry breaking interaction. In this antiferromagnet on the square lattice we divide the whole lattice into two kinds of lattices, which are called A-lattice and B-lattice. The semi-classical order on B-lat- tice has the opposite sign against that on A-lattice. Therefore the symmetry breaking interaction is a sum of the local spin operators with positive signs for the spin on A-lattice and those with negative signs for spins on B-lattice. Taking that is defined as the total sum of into account, the Hamiltonian which includes is given by
(12)
Here denotes the nearest neighbor pair on the square lattice, and we define
(13)
Note that this system has SU(2) symmetry for , while it has U(1) symmetry when .
In order to make a diagonal matrix, the basis state is defined by where with or . We replace the state at each site by the vector representation. Then the spin operators with x-, y- and z-components are represented by the Pauli matrix ,
(14)
One reason for adopting this representation is that any state is the eigen state of . Another reason is that in the analysis by spin wave theory [25] we would like to use the real matrix element on .
In order to calculate the ground state in terms of the quasi-degenerate state where , we need the matrix elements of between these states. They are
(15)
Here
(16)
Note that in (16) is independent of the site because has the translational symmetry. Other matrix elements of the Hamiltonian are zero.
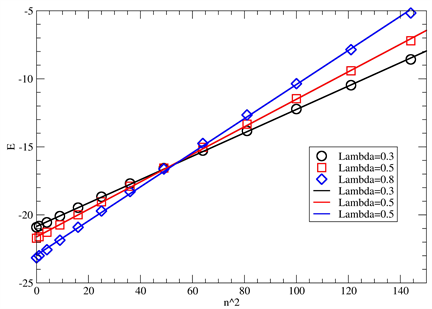
The energy in (15) is given by the expression (6) [24] [28] . Since this expression is quite important for our study on the cluster property, we present numerical results on lattice in Figure 1, which are calculated by the exact diagonalization. We find that the expression (6) is valid even for the small size lattice of . Also numerical studies on lattice show that n dependence of is given by
(17)
In addition, from results on lattices of , we observe that , and . Using the least square fit for data on these lattices, we estimate that , and for .
In the following sections we suppose that the lattice size N is quite large. Therefore hereafter we use, instead of (15),
(18)
Figure 1. The energy of the quasi-degenerate state with the quantum number n of U(1) symmetry. In the horizontal axis we show . Black circles, red squares and blue diamonds show the energy calculated by the exact diagonalization on the lattice with and 0.8. Solid lines are results of the least square fits.
4. Ground State with Symmetry Breaking Interaction
Here we consider the set of the quasi-degenerate states,
(19)
The ground state is the linear combination of ,
(20)
From (18) and (20) the eigen equation can be replaced by the eigen equation on ,
(21)
We assume that the coefficient changes smoothly on n. Then we can replace n by a continuous variable , and replace by a continuous function ,
(22)
By this correspondence we have
(23)
Here with a good approximation we replace the discrete operation by the differential one in the above equation. Therefore we obtain the following equation for the eigen equation on ,
(24)
This eigen equation leads
(25)
In the above equation, we do not drop any term yet.
When is of order of with we can drop terms from third to the seventh of the left hand side of the equation. The reasons are as fol
lows. The third term is of the second term. The ratios of the 4-th and the 5-th term to the first term are and , respectively. The 6-th term is
of the second term. Also the 7-th term is of the second term. Therefore only the
first and the second terms remain in the left hand side of (25).
Then the equation becomes to be the wave equation with the harmonic potential,
(26)
Thus we obtain eigen functions and eigen values,
(27)
(28)
Here is the l-th Hermite polynomial, is a normalization factor
calculated by and
(29)
The ground state is given by , more precisely,
(30)
The ground state energy is given from (28) by
(31)
Here the constants a, f and v are fixed once the Hamiltonian of the model is given. The parameter that we can control is g only. In the next section we will analyze the effects by the breaking interaction to the spin correlation function.
5. Spin Correlation Function
For our study of the cluster property, we introduce the spin correlation function and its difference ,
(32)
If the cluster property holds, we have .
The most important assumption in our calculations is that the spin correlation is the sum of the contribution due to Nambu-Goldstone mode and that due to the quasi-degenerate states. Namely we assume that
(33)
In Appendix B we will show the basis of this assumption.
In the next subsection we calculate the spin correlation function due to Nambu-Goldstone mode. In subsection 5.2 we calculate the spin correlation function due to the quasi-degenerate states.
5.1. Calculation by Spin Wave Theory
When we add the symmetry breaking interaction to the Hamiltonian, this interaction changes the gapless Nambu-Goldstone mode to the gapped state. For quantitative calculations about the gapped state, we employ linear spin wave theory (LSWT) [25] . The Hamiltonian of the model with spin S is given by
(34)
After introducing
(35)
we replace the spin operators by the annihilation operators and the creation operators for the magnon,
(36)
Using and , Hamiltonian in (34) becomes
(37)
We use instead of for the representation by the wave vector,
(38)
Here the wave vector is defined by , using integer and . Then we describe the Hamiltonian by and , with and ,
(39)
We diagonalize the Hamiltonian by
(40)
Then we obtain
(41)
Here the parameter is determined by
(42)
Then the energy of the magnon is given by
(43)
We would like to obtain the spin correlation function at the large distance on the quite large lattice. Therefore we are interested in the small wave vectors. In the case of and , the energy is given by
(44)
We see that the gap energy is proportional to when g is small. By this gap energy we expect that the spin correlation function decreases exponentially at the large distance.
Let us explicitly calculate the spin correlation function of the spin operator
. For this calculation we express the spin operator by the operators and ,
(45)
Here we introduce notation defined by
(46)
Using this expression for , we can calculate the spin correlation
function due to Nambu-Goldston mode. It is clear from (45) that
(47)
In addition we obtain
(48)
When the distance is large, the summation on can be dominated by the contributions from the small wave vector. Therefore we can replace the energy by
(49)
For large r the summation can be replaced by the integral in a good approximation,
(50)
Here is the Bessel function. Since the integral of the Bessel functions is equal to , we obtain the simple expression.
5.2. Correlation Function Due to Quasi-Degenerate States
In this subsection we calculate the spin correlation function induced by the quasi-degenerate states. We start with the ground state (30) which is derived from (20), and the matrix element
(51)
In the Hilbert space spanned by the quasi-degenerate states,
(52)
Since N is quite large, we can replace the discrete expression by the differential expression. Clearly we have
(53)
In addition we obtain
(54)
From (54) we see the following.
1) is independent on the distance , which implies that this correlation function is not zero even if r is large.
2) is of order of . Therefore it strongly depends on the magnitude of the strength g of the symmetry breaking interaction.
Keeping fixed, we obtain the following results even if we make the size N infinitely large,
(55)
Therefore the spin correlation function violates the cluster property.
6. Cluster Property
As described in (33) the spin correlation function is the sum of the function due to Nambu-Goldstone mode and one due to the quasi-degenerate states. In addition the expectation value of the single spin operator is zero, as is shown in subsections 5.1 and 5.2. Therefore we see that
(56)
Here we obtain by putting in (50).
In numerical estimations we suppose because the additional interaction should be small. For we have . In addition, with , we have
(57)
Since the lattice size N is fixed to be 1020, the parameter in (56) is only the strength g of the additional interaction.
As described in subsection 5.2, violates the cluster property. Experiments to observe this violation are nontrivial tasks, however. One reason is that will be small if we cannot suppress the additional interaction small enough. Another reason is that will be hidden by unless . Taking these difficulties into account, we discuss what conditions make be measurable.
First we estimate in (56), which is for small g. Its magnitude increases when g decreases. For example when g is 10−8, is , while when g is 10−32, is .
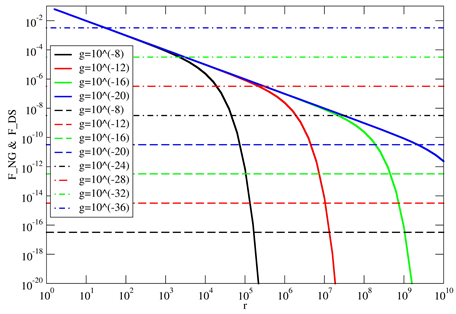
In order to observe a signal for the violation of the cluster property, we need a condition that in (56) is smaller than . In Figure 2 we plot and as a function of the distance r for various values of g, which helps us to estimate this condition quantitatively. Let us consider three typical cases which are , and .
1)
As we see in Figure 2, decreases rapidly . Then we find a possibility to observe at this distance. We have to measure, however, very small which is of order of 10−17.
2)
In this case shows not the rapid decrease but the decrease following 1/r. is larger than only when r is larger than 108. We see the narrow range of r where the observation of is possible.
Figure 2. The correlation and which are shown as functions of the distance r. Values of agree with the blue curve when . The parameter is 0.5 and the lattice size is .
3)
This value of g is extremely small so that is of order of 10−5. Since , is larger than at the distance . Therefore it would be easy to observe the signal of the violation of the cluster property.
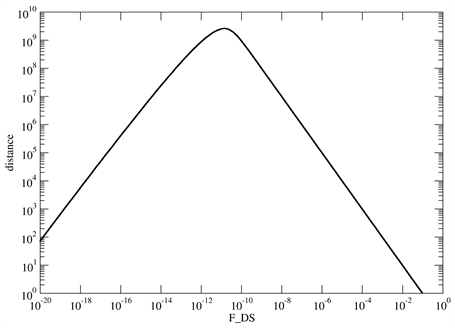
The above discussion shows the importance of the distance r at which we observe the spin correlation function. Therefore in Figure 3 we plot, as a function of the value of , the distance r where is equal to . In this figure we find the triangle curve above which . Let us see r for several concrete cases.
1) ( )
Note that decreases exponentially at Therefore if this small value of the spin correlation function is observable in experiments, we can find the signal for in the wide range of the distance .
2) ( )
For this value we find the very narrow range of r for the possible observation of the violation. We have to measure the correlation function at the large distance near its maximum.
3) ( )
If we suppress the additional interaction until , we have the large value for . In this case the range of r for the possible observation of the violation is wide again, i.e. at the distance of we can make the measurement.
Figure 3. The distance at which the magnitude of is equal to that of . In the horizontal axis we show the magnitude of . In the region above the triangle curve, is larger than . The lattice size is and the parameter is 0.5.
In conclusion we find that the spin correlation function due to the quasi-de- generate states violates the cluster property. If we can measure very small correlations, we can catch the signal for the violation in the wide range of the distance.
7. Summary and Discussion
In this paper we made an extensive study of the cluster property in the quantum antiferromagnet on the square lattice. The cluster property means that there are no relations between two events that are sufficiently separated. For this study we kept the lattice size N finite, because the effect due to the finite size plays an important role. In this study we assign , since we consider the material of order of 1 m.
For a concrete model we adopted the S = 1/2 XXZ antiferromagnet on the square lattice. This model has U(1) symmetry which spontaneously breaks. The reason why we employ it is that we would like to analyze a model as simple as possible. On the finite lattice the lowest energy of the states with the quantum number n of the symmetry is almost the same as the energy with . When we add the interaction that explicitly breaks the symmetry, the ground state becomes the linear combination of the quasi-degenerate states, which strongly depends on the strength of the added interaction.
In order to study the cluster property we calculated the spin correlation function. It is known that the function due to Nambu-Goldstone mode satisfies the cluster property. What we showed is that the quasi-degenerate states induce another spin correlation and it violates the cluster property. This induced function is, at any distance between positions of two spin operators, of order of , where g is the strength of the additional interaction. The necessary condition to observe the violation in experiments is that the correlation function due to the quasi-degenerate states is larger than the spin correlation function due to Nambu-Goldstone mode. We showed that g required for this condition depends on the distance. Then we conclude that it is possible to find the violation of the cluster property in experiments.
Let us comment on experiments about the cluster property. In the experiments it is required to measure the correlation length [30] [31] [32] , because the correlation length is directly connected with the behavior of the spin correlation at the large distance. In the experiments on the material Sr2CuCO2Cl2 [33] [34] , the neutron scattering is used to measure the correlation length. These experiments confirmed that this correlation length becomes large when the temperature is low. In addition it turned out that the length is an exponential function of the inverse of the temperature. In these experiments it was found that the correlation length scales from 1 to 200 lattice constants when temperature decreases from 1500 K to 300 K. Therefore it is difficult to observe the violation of the cluster property in this range of the correlation length.
In experiments the growth of the correlation length is limited by temperature. In addition even if temperature is close to zero, where the correlation length is of order of the system size, the disturbed interactions limit the length. But, in principle, one can control these interactions in experiments. Therefore we would be able to examine the cluster property when the temperature is quite low and the disturbance which contains the symmetry breaking interaction is suppressed.
While we have only a few experiments on XXZ model [35] , which is the model we studied, there are many experiments [30] [31] [32] [33] [34] on Heisenberg antiferromagnet which has SU(2) symmetry. Therefore our further study should be made about the Heisenberg model. In this model the energy of the quasi-degenerate states is proportional to , where J is the total spin of the quasi-degenerate states. Since these states with a fixed J are degenerate on , where is the z-component of the total spin, we cannot determine the ground state uniquely by one kind of the interaction only. Therefore we need a detailed study on additional interactions to obtain the unique ground state. Then we have to make quantitative estimations for the violation of cluster property using these interactions.
Acknowledgements
The author is very grateful to Dr. Yasuko Munehisa for all her comments and suggestions to improve this paper through critical reading of the manuscript.
Cite this paper
Munehisa, T. (2018) Violation of Cluster Property in Quantum Antiferromagnet. World Journal of Condensed Matter Physics, 8, 1-22. https://doi.org/10.4236/wjcmp.2018.81001
References
- 1. Horodecki, R., Horodecki, P., Horodecki, M. and Horodecki, K. (2009) Quantum Entanglement. Review of Modern Physics, 81, 865. https://doi.org/10.1103/RevModPhys.81.865
- 2. Nielsen, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University, Cambridge.
- 3. Guhne, O. and Toth, G. (2009) Entanglement Detection. Physics Reports, 474, 1-75. https://doi.org/10.1016/j.physrep.2009.02.004
- 4. Ekert, A., Alves, C., Oi, D., Horodecki, M., Horodecki, P. and Kwek, L. (2002) Direct Estimations of Linear and Nonlinear Functionals of a Quantum State. Physical Review Letters, 88, 217901. https://doi.org/10.1103/PhysRevLett.88.217901
- 5. Napoli, C., Bromley, T.R., Cianciaruso, M., Piani, M., Johnston, N. and Adesso, G. (2016) Robustness of Coherence: An Operational and Observable Measure of Quantum Coherence. Physical Review Letters, 116, 150502. https://doi.org/10.1103/PhysRevLett.116.150502
- 6. Van Raamsdonk, M. (2010) Building up Spacetime with Quantum Entanglement. General Relativity and Gravitation, 42, 2323-2329. https://doi.org/10.1007/s10714-010-1034-0
- 7. Calabrese, P. and Cardy, J. (2009) Entanglement Entropy and Conformal Field Theory. Journal Physics A, 42, 504005. https://doi.org/10.1088/1751-8113/42/50/504005
- 8. Nishioka, T., Ryu, S. and Takayanagi, T. (2009) Holographic Entanglement Entropy: An Overview. Journal Physics A, 42, 504008. https://doi.org/10.1088/1751-8113/42/50/504008
- 9. Anderson, P.W. (1984) Basic Notions of Condensed Matter Physics. Benjamin/Cummings, Menlo Park, CA.
- 10. Weinberg, S. (1995) The Quantum Theory of Fields. Vol. 2, Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781139644167
- 11. Amico, L., Fazio, R., Osterloh, A. and Vedral, V. (2008) Entanglement in Many-Body Systems. Review of Modern Physics, 80, 517. https://doi.org/10.1103/RevModPhys.80.517
- 12. Islam, R., Ma, R., Preiss, P.M., Tai, M.E., Lukin, A., Rispoli, M. and Greiner, M. (2015) Measuring Entanglement Entropy in a Quantum Many-Body System. Nature, 528, 77. https://doi.org/10.1038/nature15750
- 13. Cianciaruso, M., Ferro, L., Giampaolo, S.M., Zonzo, G. and Illuminati, F. (2014) Classical Nature of Ordered Phases: Origin of Spontaneous Symmetry Breaking. https://arxiv.org/abs/1408.1412
- 14. Shi, Y. (2003) Quantum Disentanglement in Long-Range Orders and Spontaneous Symmetry Breaking. Physics Letters A, 309, 254-261. https://doi.org/10.1016/S0375-9601(03)00128-2
- 15. Heaney, L., Anders, J., Kaszlikowski, D. and Vedral, V. (2007) Spatial Entanglement From Off-Diagonal Long-Range Order in a Bose-Einstein Condensate. Physics Review A, 76, 053605. https://doi.org/10.1103/PhysRevA.76.053605
- 16. Hamma, A., Giampaolo, S. and Illuminati, F. (2016) Mutual Information and Spontaneous Symmetry Breaking. Physics Review A, 93, 012303. https://doi.org/10.1103/PhysRevA.93.012303
- 17. Strocchi, F. (2008) Symmetry Breaking. Lecture Note Physics 732. Springer, Berlin.
- 18. Strocchi, F. (1978) Local and Covariant Gauge Quantum Field Theories. Cluster Property, Superselection Rules, and the Infrared Problem. Physics Review D, 17, 2010-2021. https://doi.org/10.1103/PhysRevD.17.2010
- 19. Lowdon, P. (2016) Conditions on the Violation of the Cluster Decomposition Property in QCD. Journal of Mathematical Physics, 57, 102302. https://doi.org/10.1063/1.4965715
- 20. Xu, S. and Fan, S. (2017) Generalized Cluster Decomposition Principle Illustrated in Waveguide Quantum Electrodynamics. Physics Review A, 95, 063809. https://doi.org/10.1103/PhysRevA.95.063809
- 21. Froehlich, J. and Rodriguez P. (2017) On Cluster Properties of Classical Ferromagnets in an External Magnetic Field. Journal of Statistical Physics, 166, 828-840. https://doi.org/10.1007/s10955-016-1556-2
- 22. Shimizu, A. and Miyadera, T. (2002) Cluster Property and Robustness of Ground States of Interacting Many Bosons. Journal of the Physical Society of Japan, 71, 56-59. https://doi.org/10.1143/JPSJ.71.56
- 23. Shimizu, A. and Miyadera, T. (2002) Stability of Quantum States of Finite Macroscopic Systems against Classical Noises, Perturbations from Environments, and Local Measurements. Physical Review Letters, 89, 270403. https://doi.org/10.1103/PhysRevLett.89.270403
- 24. Richter, J., Schulenburg, J. and Honecker, A. (2004) Quantum Magnetism. In: Schollwock, U., Richter, J., Farnell, D.J.J. and Bishop, R.F., Eds., Lecture Note in Physics, Volume 645, Springer-Verlag, Berlin Heidelberg, 85-153.
- 25. Auerbach, A. (1994) Interacting Electrons and Quantum Magnetism. Springer-Verlag, Berlin Heidelberg. https://doi.org/10.1007/978-1-4612-0869-3
- 26. Hatano, N. and Suzuki, M. (1993) Quantum Monte Carlo Methods in Condensed Matter Physics. World Scientific, Singapore, 13-47. https://doi.org/10.1142/9789814503815_0002
- 27. De Raedt, H. and von der Linden, W. (1995) The Monte Carlo Method in Condensed Matter Physics. Springer-Verlag, Berlin Heidelberg, 249-284.
- 28. Manousakis, E. (1991) The Spin-1/2 Heisenberg Antiferromagnet on a Square Lattice and Its Application to the Cuprous Oxides. Review Modern of Physics, 63, 1. https://doi.org/10.1103/RevModPhys.63.1
- 29. Landee, C. and Turnbull, M. (2013) Recent Developments in Low-Dimensional Copper(II) Molecular Magnets. European Journal of Inorganic Chemistry, 2013, 2266-2285. https://doi.org/10.1002/ejic.201300133
- 30. Birgeneau, R.J., Greven, M., Kastner, M.A., Lee, Y. Wells, B.O., Endoh, Y., Yamada, K. and Shirane, G. (1999) Instantaneous Spin Correlations in La2CuO4. Physical Review B, 59, 13788. https://doi.org/10.1103/PhysRevB.59.13788
- 31. Tseng, K., Keller, T., Walters, A., Birgeneau, R. and Keimer, B. (2016) Neutron Spin-Echo Study of the Critical Dynamics of Spin-5/2 Antiferromagnets in Two and Three Dimensions. Physics Review B, 94, 014424. https://doi.org/10.1103/PhysRevB.94.014424
- 32. Bossoni, L., Carretta, P., Nath, R., Moscardini, M., Baenitz, M. and Geibel, C. (2011) NMR and μSR Study of Spin Correlations in SrZnVo(PO4)2: An S = 1/2 Frustrated Magnet on a Square Lattice. Physics Review B, 83, 014412. https://doi.org/10.1103/PhysRevB.83.014412
- 33. Greven, M., Birgeneau. R.J., Endoh, Y., Kastner, M., Keimer, B., Matsuda, M. Shirane, G. and Thurston, T. (1995) Spin Correlations in the 2D Heisenberg Antiferromagnet Sr2CuO2Cl2: Neutron Scattering, Monte Carlo Simulation, and Theory. Physics Review Letters, 72, 1096-1099. https://doi.org/10.1103/PhysRevLett.72.1096
- 34. Greven, M., Birgeneau. R.J., Endoh, Y., Kastner. M., Matsuda, M. and Shirane, G. (1995) Neutron Scattering Study of the Two-Dimensional Spin S = 1/2 Square-Lattice Heisenberg Antiferromagnet Sr2CuO2Cl2. Zeitschrift für Physik B Condensed Matter, 96, 465-477. https://doi.org/10.1007/BF01313844
- 35. Xiao, F., Woodward, F., Landee, C., Turnbull, M., Mielke, C., Harrison, N., Lancaster, T., Blundell, S., Baker, P., Babkevich, P. and Pratt, F. (2009) Two-Dimensional XY Behavior Observed in Quasi-Two-Dimensional Quantum Heisenberg Antiferromagnets. Physics Review B, 79, 134412. https://doi.org/10.1103/PhysRevB.79.134412
Appendix A
In this appendix we show the relation between entanglement and the cluster property in spin systems. Entanglement is judged to be large when the two- Renyi mutual information [4] [16] is large. Here is defined by the entropy ,
(58)
The entropies are calculated by the density matrix ,
(59)
As a result entanglement is measured by the density matrix at the local positions. In the S = 1/2 quantum systems, where temperature is zero, the density matrix at the local position is given by the sum of the expectation values of the spin operator in the ground state [16] ,
(60)
Here . Also the density matrix is calculated by the correlation function of the spin operators in the ground state,
(61)
Then the square products of the density matrices become
(62)
Since and , the traces of and are given by
(63)
Let us calculate the information at large distance when the cluster property holds. In this case we have
(64)
Therefore with large we have
(65)
Then we obtain
(66)
As a result the information is zero.
Next we calculate the information at large distance when the cluster property fails. In this case we have, with a non-zero constant ,
(67)
With large we have, if ,
(68)
Then
(69)
Therefore at the large distance we obtain the information which is given by
(70)
It shows that the violation of the cluster property lead to the non-zero at the large distance. Reversely the large entangled correlation in the far distance leads to the violation of the cluster property. Because of this equivalence the study on cluster property is interesting in the application to the quantum communication.
Appendix B
In this appendix we make a brief discussion to give the basis on our assumption (33) which means that the spin correlation function is the sum of the function due to due Nambu-Goldstone mode and the one due to the quasi-degenerate states. Here we neglect, for the quite large N, the terms with .
In Section 2 we described two properties originating from the quasi-degene- rate states , which are the quasi-degeneracy on the energy and the non-
zero matrix elements . As is shown in (11), the latter implies . Based on this result and the translational sym-
metry of , it is derived that Nambu-Goldstone mode exists and contains this mode [10] .
It should be noted that, in this derivation, there is no restriction to the number of the quasi-degenerate states which the ground state consists of. An extreme example is that the ground state is the linear combination of only two quasi-de- generate states and with some n,
(71)
Even in this case we do have Nambu-Goldstone mode, since
(72)
Therefore each contains Nambu-Goldstone mode having wave vector and its energy proportional to . The spin correlation function due to Nambu-Goldstone mode at the large distance is determined only by the mode with small values of .
Let us denote the annihilation (creation) operator of Nambu-Goldstone mode with by ( ). The spin operator includes a function of and , which we denote by here. Note that in SWT approximation is given by (45).
Since and , should include an additional operator defined by
(73)
Note that does not depend on i. Thus we have
(74)
Therefore we obtain
(75)
We also obtain
(76)
The third term is equal to zero because
(77)
Similarly the forth term vanishes. Thus we justify the assumption (33).