Received 8 June 2016; accepted 22 July 2016; published 25 July 2016

ABSTRACT

Nonequilibrium effect due to the imbalance in the number of the ­ and ¯ spin electrons has been studied for the tunneling currents in the ferromagnet-insulator-superconductor (FIS) tunneling junctions within a phenomenological manner. It has been stated how the nonequilibrium effect should be observed in the spin-polarized quasiparticle tunneling currents, and pointed out that the detectable nonequilibrium effect could be found in the FIS tunneling junction at 77 K using HgBa₂Ca₂Cu₃O_8+d (Hg-1223) high-T_c superconductor rather than Bi₂Sr₂CaCu₂O_8+d (Bi-2212) one.

Keywords:

Nonequilibrium Effect, Ferromagnet-Insulator-Superconductor Tunneling Junction, Hg-1223, Bi-2212, Spin-Polarized Quasiparticle Tunneling

1. Introduction

Transition from an equilibrium to non-equilibrium state due to an external perturbation makes an output. The well known case is the transport phenomena, which can be understood by solving the Boltzmann equation for classical treatment and the Liouville equation for quantum one. Even in superconductors, the departure from the equilibrium state of the distribution function is found when the superconductors are set in the time and/or spatial modulations as an external perturbation. Such a situation, the nonequilibrium superconductivity, can be understood as a change of superconducting parameters induced by modifications of the distribution function of quasiparticle excitations. Studies for the nonequilibrium superconductivity have focused on the effects of not only the simple quasiparticle injection and extraction but also the spin-polarized quasiparticle transport. The valuable considerations have already been done by Tinkham [1] . In the case of simple quasiparticles, the phenomena can be described by introducing two parameters T^* and Q^* which represent the nonequilibrium temperature and quasiparticle charge density, respectively. In the case of the injection of spin-polarized quasiparticles, such as the quasiparticle tunneling in the ferromagnet-insulator-superconductor (FIS) tunneling junction, one can experimentally see the suppression of superconductivity whose origin is regarded as a pair-breaking mechanism of a Cooper-pair (CP).

CalTech group has extensively studied the nonequilibrium superconductivity under spin-polarized quasiparticle currents in the FIS tunneling junctions, and found that the phenomena manifesting nonequilibrium superconductivity in perovskite FIS heterostructure are observed and are attributed to the dynamic pair-breaking effect of spin-polarized quasiparticles in cuprate superconductors [2] [3] . We have experimentally studied the variation of the critical current I_c of intrinsic Josephson junctions due to the spin injection and found that the observed modulation of I_c of Co/Au/Bi₂Sr₂CaCu₂O_y mesa is attributed to the injection of the spin-polarized current [4] [5] . Recently, we have theoretically studied the charge and spin currents in FIS tunneling junction [6] and the spin flows in magnetic semiconductor-insulstor-superconductor (MS-I-S) tunneling junction [7] and found that the adopted MS-I-S tunneling junction seems to work as a switching device in which the spin up and down flows can be easily controlled by the external magnetic field [7] .

Spintronics including not only the ferromagnets but also superconductors is one of the most attractive subjects in solid state physics and technology. Therefore, it is surely expected that such a research will grow rapidly. For example, Kaiser and Parkin have measured the tunneling spin polarization using a superconducting tunneling spectroscopy for Al₂O₃ tunnel barriers [8] . Rudenko et al. have observed the giant growth of the differential resistance using a tunnel junction consisting of superconducting lead with Heusler’s ferromagnetic alloy Co₂CrAl, and pointed out that this effect is attributed to the appearance of a nonequilibrium state in the lead film as a result of spin injection into the superconductor [9] .

Fundamental aspects of the proximity effect under nonequilibrium conditions even in normal metal-super- conductor bilayers are not clear [10] . In the present paper, we phenomenologically study how the nonequilibrium effect due to spin injection should be observed in the spin-polarized quasiparticle tunneling along the c-axis of the FIS tunneling junctions. As a F layer, a ferromagnetic CrO₂ is selected because of its half metallic nature, i.e., a purely spin polarized, and HgBa₂Ca₂Cu₃O_8+d (Hg-1223) and Bi₂Sr₂CaCu₂O_{8 + d} (Bi-2212) high-T_c superconductors are adopted as a S layer. Hg-based superconducting cuprates form a series with the general formula HgB₂C_n−1CunO_2n+2+d denoted as Hg-12mn 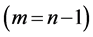with mainly Ba and Ca on the B and C sites, respectively. On increasing the number n of conducting CuO₂ layers, the transition temperature T_c progressively increases, reaching the maximum for Hg-1223 with a value of 135 K, and then decreases. The amplitude 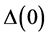at low temperature of the superconducting gap of Hg-1223 is 75 meV [11] . The structure of Bi-based superconducting cuprates form a series with the general formula Bi₂B₂C_n−1CunO_2n+4+d denoted as Bi-22mn with mainly Sr and Ca on the B and C sites, respectively. The T_c increases with an increasing number n of CuO₂ layers up to 110 K for Bi-2223. The T_c and 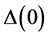of Bi-2212 we consider here are 86 K and 28 meV, respectively [11] . The crystal structures of Hg-1223 and Bi-2212 differ to each other, but there is a common feature such that these superconductors called “cuprate superconductors” include CuO₂ layers showing a superconductive property. From the symmetry consideration for the CuO₂ layer, these cuprate superconductors show the superconducting gap with 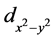-symmetry so that the CPs are in a spin-singlet state.

It is considered for the present study that 1) the electron states in the vicinity of the Fermi level E_F mainly come from 3d orbitals of Cu and Cr atoms; 2) the density of states (DOS) that originated from the 3d orbital shows a pointed structure meaning the localized nature, on the contrary to the DOS from s and p orbitals which show a broadened structure, i.e., the extended nature; therefore 3) the effective mass approximation, which is valid for the extended nature, may not be so good for the present system in which the electron states near the E_F are fairly well localized; and 4) the size of the insulating layer I is a realistic one, whose barrier strength is large enough, so it must be noted that 5) Blonder, Tinkham and Klapwijk (BTK) model [12] reaches to the tunneling Hamiltonian model since the probability of Andreev reflection decreases with the increasing the barrier strength of the I layer. In the present paper, therefore, the tunneling Hamiltonian model based on the electrons with the Bloch states decided from the band structure calculations is adopted.

2. Theoretical

Tunneling current 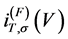with a given spin 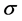(= ­ or ¯) in the FIS tunneling junction is given as a function of an applied voltage V as follows [6] [7] ;

(1)

Here note that the S shown in Equation (1) is a symbol to identify the superconductor so that this symbol is used everywhere in the present paper. The charge and spin currents, 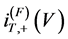and, are calculated as

(2)

where C is a constant given by and. In the present paper, we consider the none-

quilibrium effect on the charge current. The 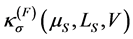is defined as

(3)

where is the first Brillouin zone of S. The is the coefficient in the expansion by the Bloch orbitals of the total wavefuntion of S such as

(4)

where and are the site to be considered and the quantum state of atomic orbital of S, respectively.

The in Equation (3) is the tunneling probability of a s-spin electron in the FIS tunneling junction defined by

(5)

so that the value of 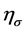strongly depends on the magnetic nature of an insulating layer I. As the I, we consider here the non-magnetic layer, thus the tunneling probabilities of majority (­) and minority (¯) spin electrons must be equal each other, i.e.,.

As a tunneling process, coherent, incoherent and WKB cases can be considered. In the present paper, the incoherent tunneling is mainly studied. The reason is described later. In the incoherent tunneling case, the in Equation (3) denoted as is given by [6]

(6)

where f is a Fermi-Dirac distribution function and is the TDOS of the F layer for spin state as a

function of energy. The is a quasiparticle excitation energy defined by, where the is an

one electron energy relative to the Fermi level and the is a superconducting energy gap given by with a sample temperature T_samp.

The one electron energy is calculated on the basis of the band theory using a universal tight-binding parameters (UTBP) method proposed by Harrison [13] . The energies of the atomic orbitals used in the band structure calculations have been calculated by using the spin-polarized self-consistent-field (SP-SCF) atomic structure calculations based on the Herman and Skillman prescription [14] using the Schwarz exchange correlation parameters [15] .

3. Results and Discussion

First of all, we must check how the current-voltage (I-V) characteristics are changed due to the change of tunneling mechanism such as coherent, incoherent and WKB ones. In order to do so, we have calculated the I-V characteristics of the FIS tunneling junction for these three cases, where the F is the ferromagnetic CrO₂ with a half metal phase, the I is a nonmagnetic insulating layer with a real dimensional size, and the S is the Hg-1223 high-T_c superconductor. Here we wish to emphasize that the numerical calculations for the coherent and WKB cases need a very large CPU time as compared with the incoherent case [6] . The’s at T_samp = 4.2 K calculated for above three cases have told us that 1) the result calculated for the coherent case shows a unrealistic behavior so that there are some regions in which the differential conductance dI/dV is calculated as a negative value, 2) that for the incoherent case is reasonable, and 3) that for the WKB case is fairly similar to that for the incoherent one, but there are regions in which the dI/dV is calculated as a negative value. From above, we consider here only the incoherent tunneling case.

Next, we must consider the effect of the external magnetic field. In the present paper, the FIS tunneling junction, in which the F-layer shows a magnetization because of a half metallic CrO₂ so that the spin-polarized quasiparticle injection has been well done for no applied field, is considered. Generally, the magnetic field has an obvious effect on the transition temperature T_c and superconducting gap Δ, however, the external magnetic field we consider here is a field made by the magnetization of the CrO₂-layer. Therefore, it seems that the effect of the external magnetic field may be small. In the present paper, thus, its effect has been taken into account by using the same method done by Tedrow and Meservey [16] . Namely, the quasiparticle excitation energy E_k has been replaced by for the majority and the minority spin, respectively. Actually, we did a calculation for the external magnetic induction B_ext with the value of 1 T, and found that there is no detectable difference between the calculations for and 1 T. In the present paper, therefore, the effect of the external magnetic field has not been considered anymore. In the following, therefore, we consider only the incoherent tunneling case with no external magnetic field.

Experimental current is proportional to the calculated one. Therefore, if the logarithmic derivative is taken for both currents, then a following relation is held

(7)

This relation clearly shows that the logarithmic derivative LD calculated by using numerically calculated values is exactly equal to that by using the experimental one. In the following, therefore, we show only the LD values deduced from the full numerically calculated charge current.

In the FIS tunneling junction, it is easily supposed that the imbalance in the number of the ­ and ¯ spin electrons makes a decrease in the number of CPs. This is just a nonequilibrium effect that we consider here. The decrease in the number of CPs makes a decrease in the amplitude of the superconducting gap, where. Therefore, in order to take into account the influence of such a nonequilibrium effect, we introduce a parameter with a value between 0 and 1, by which the is reduced to. Here note that is equal to the parameter we have introduced previously [7] . It is clear that the condition means the no consideration for the nonequilibrium effect due to the imbalance in the number of the ­ and ¯ spin electrons. The parameter directly reflects the imbalance in spin population, so it must be noted that the should be treated separately apart from the parameter T^* which represents the nonequilibrium temperature. At low temperature region, the nonequilibrium effect we consider here should be small and its temperature variation may also be small because of a huge number of CPs at the low temperature region. Therefore, it may be reasonable to suppose that and. For the, thus, we a priori assume that

(8)

where is an adjustable parameter with. Equation (8) is just a phenomenological.

The differences LD_FIS − LD_NIS of the logarithmic derivatives LD_FIS and LD_NIS deduced from the charge currents calculated for the FIS and NIS tunneling junctions are shown in Figures 1(a)-(f). Figure 1(a), Figure 1(b) and Figure 1(c) are results obtained by using a ferromagnetic half metal CrO₂ as F, an Al metal as N and a HgBa₂Ca₂Cu₃O_8+d (Hg-1223) high-T_c superconductor as S, and (d), (e) and (f) are those by using the CrO₂ as F, the Al as N and a Bi₂Sr₂CaCu₂O_{8 + d} (Bi-2212) high-T_c superconductor as S. As already stated, the T_c of Hg-1223 and Bi-2212 is 135 and 86 K, and the of those are 75 and 28 meV, respectively [11] . In order to make a comparison with the experiment, it is important to define the sample temperature T_samp even in the theoretical studies. In the present calculations, therefore, the reduced sample temperature has been selected as 0.1 for Figure 1(a) and Figure 1(d), 0.5 for Figure 1(b) and Figure 1(e), and 0.9 for Figure 1(c) and Figure 1(f), tentatively. Therefore, for Figures 1(a)-(f), the realistic sample temperature T_samp is 13.5, 67.5, 121.5, 8.6, 43.0 and 77.4 K, and the resultant is 75, 72, 40, 28, 27 and 15 meV, respectively. The horizontal axis is the normalized voltage V_N defined by and the vertical one is the LD in unit

of. The numerical calculations have been done at no external magnetic field and a voltage interval −5 ≤ V_N ≤ 5, so it must be noted that the real voltage differs for all. The with the values of 0, 0.5 and 1 has been selected tentatively, and the corresponding curves have been drawn by red, blue and green colors, respectively. The condition means the no consideration for the nonequilibrium effect due to the imbalance in the number of the ­ and ¯ spin electrons, so it is clear that (1) the structures found in curves drawn by red color with are caused to the difference between the densities of states of a ferromagnetic half-metal Cr and a normal simple metal Al and (2) the change of curves due to the increase of directly shows the nonequilibrium effect due to the imbalance of the spin population. The calculations show that (1) the nonequilibrium effect is found at τ_samp = 0.5 and 0.9, and (2) the remarkable change is found in Hg-1223 high-T_c superconductor rather than Bi-2212 one. This is caused to the fact that the of Hg-1223 superconductor is fairly larger than that of Bi-2212 one. We have a priori assumed that the phenomenological parameter γ can be regarded as a function of only the τ. However, there is a fact that the CP becomes much stable due to the increase of the superconducting gap, and there are some theoretical studies for the superconducting gap such that the spin-exchange interaction could be considered as a one of the origins of the attractive interaction for CP [17] - [23] . Therefore, it may be reasonable to suppose that the γ should also be correlated with the superconducting gap Δ, that is, γ may be a function such as. Only the experimental study can clarify this conjecture.

In order to make a comparison with the experimental study, we have chosen two temperatures 4.2 and 77 K as a T_samp and calculated the LD_FIS and LD_NIS. The results for the difference LD_FIS − LD_NIS are shown in Figures 2(a)-(d). Figure 2(a) and Figure 2(b) are results obtained by using FIS and NIS tunneling junctions with a CrO₂ as F, an Al metal as N and a HgBa₂Ca₂Cu₃O_8+d (Hg-1223) high-T_c superconductor as S, and (c) and (d) are those with the CrO₂ as F, the Al as N and a Bi₂Sr₂CaCu₂O_8+d (Bi-2212) high-T_c superconductor as S. The T_samp is 4.2 K for (a) and (c) and 77 K for (b) and (d) and the and of Hg-1223 are 75 and 69.7 meV, and those of Bi-2212 are 28 and 15.2 meV, respectively. The horizontal axis of Figure 2 is in the real voltage, so it should be emphasized that the calculated results can be directly compared with the experimental ones. Figure 2 shows that (1) the nonequilibrium effect due to the imbalance in the number of the ­ and ¯ spin electrons is not found at 4.2 K as is shown in (a) and (c), but is found at 77 K in (b) and (d), and (2) its effect is clearly found in (b), that is, the case of the FIS tunneling junction using Hg-1223 superconductor at 77 K.

At the high voltage region, the I-V curve of FIS tunneling junction approaches to the ohmic line. Namely, the effect of the variation of superconducting gap decreases with an increasing the voltage applied to the junction.

This is a reason why the value of LD_FIS − LD_NIS at the high voltage region remains the same for the change of the, as is shown in Figure 1 and Figure 2.

Our phenomenological approach for the nonequilibrium effect states that if the experiments for the difference LD_FIS − LD_NIS using the CrO₂ as F, the Al as N and the Hg-1223 high-T_c superconductor as S are done at two temperatures such as 4.2 and 77 K and the detectable differences are found at these temperatures, then such a difference is directly correlated with the nonequilibrium effect due to the imbalance in the number of the ­ and ¯ spin electrons.

4. Summary

For the c-axis tunneling currents observed in the ferromagnet-insulator-superconductor (FIS) tunneling junctions, we have phenomenologically studied the nonequilibrium effect due to the imbalance in the number of the ­ and ¯ spin electrons, in order to see how the nonequilibrium effect due to spin injection should be observed in the spin-polarized quasiparticle tunneling. We have showed that 1) the nonequilibrium effect is found at 77 K rather than 4.2 K, and 2) its effect is clearly found in the FIS tunneling junction using the Hg-1223 high-T_c superconductor rather than Bi-2212 one as S.

Cite this paper

Michihide Kitamura,Kazuhiro Yamaki,Akinobu Irie, (2016) Nonequilibrium Effect in Ferromagnet-Insulator-Superconductor Tunneling Junction Currents. World Journal of Condensed Matter Physics,06,169-176. doi: 10.4236/wjcmp.2016.63018

References