World Journal of Condensed Matter Physics
Vol.05 No.04(2015), Article ID:60214,11 pages
10.4236/wjcmp.2015.54026
A Resolution of the Black Hole Information Paradox via Transfinite Set Theory
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 September 2015; accepted 9 October 2015; published 12 October 2015
ABSTRACT
A black hole is essentially a relativistic as well as a quantum object. Therefore the information paradox of black holes is a consequence of the clash between these two most fundamental theories of modern physics. It is logical to conclude that a resolution of the problem requires some form of a quantum gravity theory. The present work proposes such a resolution using set theory and pointless spacetime geometry.
Keywords:
Information Paradox, Black Holes, S. Hawking, G. ‘t Hooft, L. Susskind, Transfinite Set Theory, Noncommutative Geometry, Measure Concentration, Dvoretzky’s Theorem, Dark Energy, Casimir Effect, Nano Casimir Reactor

1. Introduction
Physically empty space with no matter, virtual particles or radiation what so ever is still far from being nothing [1] [2] . Empty spacetime in the above sense is a sophisticated sloika, i.e. Mille-Feuill of empty sets [1] -[20] . A point in such space is by no means the classical point defined somewhat naively as the intersection of two lines [7] . In fact a proper spacetime, which satisfies the physical quantum reality, is a points-less spacetime with geometry and topology akin to that of von Neumann’s continuous geometry [76] [119] [132] as well as A. Conne’s noncommutative geometry [76] [132] apart from the arch typical pointless space of E-infinity Cantorian spacetime [11] -[132] . In such Cantorian-fractal geometry what appears to be a point is in actuality an entire Cantor set when magnified by sharpening the resolution of observation [33] -[130] . Combining the preceding fundamental insights gained from applying transfinite set theory and fractals to spacetime geometry with a fundamental theorem due to Aryeh Dvoretzky about measure concentration [65] -[67] , we can argue that only 4.5 percent of the information inside a black hole could be regarded as inaccessible while the rest of the 95.5 percent of the information remains on the surface of the black hole no matter how much it shrinks because in the end analysis, spacetime has no ordinary points and no matter how small such points are, they are not zero nor can they vanish into nothingness because empty spacetime is anything but nothing. In fact empty spacetime is a multi-fractal made of infinitely many empty sets with varying degrees of emptiness [1] [2] [12] . In this sense we can reconcile what appeared for a considerable time irreconcilable, namely the view point of S. Hawking [7] with all that speaks for it and speaks against it, with the clearly opposing views of L. Susskind and G. ‘t Hooft which is understandable, logical and correct, but nevertheless does not propose an alternative waterproof answer to replace that of S. Hawking’s famous but by no means entirely correct one [7] .
The paper is subdivided into three reasonably short parts. First, we introduce the required background information. Second, we sketch our basic analysis and finally we summarize our conclusions. Last but not least, it should be acknowledged from the outset that the recent revival of black hole physics and the information paradox at the prominent conference in Stockholm [133] -[135] as well as the highly influential writing of L. Susskind and G. ‘t Hooft [135] -[139] are the prime movers and motivation for the present work.
2. Physical, Mathematical and Cosmological Measure Concentration Phenomena
There are at least three well known types of measure concentration phenomena [64] -[67] [140] relevant to the present work. The first is what we could call physical measure concentration. We could give two examples for that. The first is the Faraday cage demonstrating that for a metal sphere the total electric charge is concentrated on the surface with zero change inside the sphere [7] . This fact is behind the fortunate situation that an aeroplane flying in a thunder and lightening storm can protect the passengers from being electrocuted as is the case with a car with closed doors and windows. The second example is the energy of the quantum particle-wave where 4.5% of the energy is inside the quantum wave concentrated in the quantum particle as measurable ordinary energy while the quantum wave surrounding the quantum particles possesses most of the energy density, namely 95.5% as dark energy [14] -[61] . The best example for mathematical measure concentration is the marvellous Dvoretzky’s theorem which states that in sufficiently high dimensionality, 96% of the volume of a sphere is concentrated near to its surface while the “bulk” contains only 4% of the volume [140] . Finally cosmological concentration phenomena may be found theoretically in the fact that all information of a black hole is proportional to the surface and not to the volume of the black hole as demonstrated by the Bekenstein formula [7] [138] . As a second example we could cite the work of the present author showing that the 4.5% ordinary energy of the universe can be measure “inside” the universe while the rest, the 95.5% dark energy exists mainly near to the boundary of the holographic boundary of the universe [7] [11] . It is the fact that our universe could be viewed as a giant black hole that we may argue that black holes, if they exist, will have most of its information, i.e. about 96% of the information on the surface of the black hole while 4% of the information could remain locked inside the black hole to which an outside observer will have no access.
3. The Transfinite Theory of Spacetime
To make a long, in fact very long story short, we start our journey to the exact picture of our physico-mathe- matical spacetime from the bijection formula [74] [75] .
 (1)
(1)
corresponding to von Neumann-Conne’s dimensional function [74] [75] of Penrose foliated universe, i.e. Penrose tiling. This is necessarily a fractal universe resembling a compactified holographic boundary, i.e. compactified Klein modular curve for a transfinite E8E8 Lie exceptional symmetry groups constituting our bulk [74] [75] .
Here 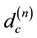 is the Hausdorff dimension corresponding to n Menger-Urysohn dimension and
is the Hausdorff dimension corresponding to n Menger-Urysohn dimension and 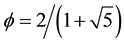 is
is
the Hausdorff dimension of the zero set, i.e. n = 0. To see that we set n = 0 in  and find [74] [75]
and find [74] [75]
 (2)
(2)
The corresponding von Neumann-Conne formula is [76]
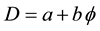 (3)
(3)
where  and
and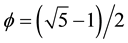 . Setting a = 0 and b = 1 one finds the same value, namely
. Setting a = 0 and b = 1 one finds the same value, namely
 (4)
(4)
This is our zero set which models the pre-quantum particle [129]
 (5)
(5)
for the pre-quantum wave, i.e. the surface or cobordism of the quantum particle we just need to insert 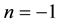 which is the dimension of the neighbourhood of a point. That way we find [74] [75]
which is the dimension of the neighbourhood of a point. That way we find [74] [75]
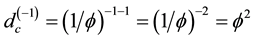 (6)
(6)
or equivalently by setting a = 1 and  one finds [74] -[76]
one finds [74] -[76]
 (7)
(7)
This is the empty set which models the quantum particle. We see that the zero set 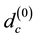 separates the sets
separates the sets  from the empty sets
from the empty sets 



4. The Menger-Urysohn Dimensionality and the Dimensions of the Empty Set d(Menger) = −1
The discussion of the section on the transfinite theory of spacetime depended crucially upon the extension of the notion of topological dimensions into the negative regime. In this section we show how simple, intuitive and easily grasped this extension of the deductive topological dimension theory which goes back to the Russian Paul Urysohn and the Austrian Karl Menger [74] -[76] . Take a 3D cube. The dimension of the cube is 3 but the dimension of the six sides of the surface of the cube is 







5. An Exact Picture of Quantum Spacetime
We clearly live in a 3 + 1 = 4 dimensional world. These are three special dimensions plus a temporal dimension preventing things from happening all at once in some folkloristic philosophy. Einstein’s special and general relativity takes the time dimension far more seriously as a dimension which one can put on equal footing as the space dimension if not even more [7] . Inserting n = 4 in our bijection formula one finds [1] [2] [74] -[76]

Consequently we have [12]

This means the fractal Hausdorff dimension is larger than the corresponding Menger-Urysohn topological dimension by the amount 

Let us look back at our spacetime as being made of an infinite mixture of all possible Cantor sets. That means starting from the unit set, i.e. classical line 


Now since 


which is the Hausdorff dimension of our spacetime. However there is a still more profound interpretation of these results because 






as well as the union of the two, namely

where 

We start with the zero set pre-particle. This is

Surrounding 

The cobordism, or surface of the guiding Bohm-Einstein quantum wave, is clearly 

Now something quite remarkable happens at this point. The particle wave entity is floating in spacetime with an average dimension 


In other words our quantum spacetime is nothing but a zero set pre-quantum particle surrounded by an empty set pre-quantum wave floating in the surface of the quantum wave given by the expectation value
6. The Casimir Local Topological Pressure
If two plates which are conducting but uncharged are put very close vis-à-vis each other, it is an experimental fact that they are pulled together by what is known as the Casimir effect [94] [120] [121] . The E-infinity set theoretical explanation advanced some time ago is as follows: The nano distance between the two plates is as near as we can come to create an empty set. That means inside the plates we have a topological pressure 





and setting the number of particles n = 0 we are left with the global part [1] -[34]

Thus we could think of 







7. Dark Energy Is Global Dvoretzky Concentration of Casimir Energy
The two Casimir plates of the classical Casimir effect experiment, plays obviously the role of a boundary condition. What happens then when this boundary is pushed to infinity? The answer is it becomes the boundary of the holographic boundary of the universe [7] . This boundary is obviously a one sided boundary with nothing outside to push back to create a statical balance. It is a Möbius-like multi-dimensional boundary and consequently the universe must expand into the insubstantial nothingness surrounding our universe which is a clopen (which means open and closed topologically) and a multiverse of its own self. Considering that this E-infinity multiverse universe has formally infinite dimensions, we see that the Dvoretzky theorem [140] will apply and as a result 95.5% of the energy of this universe will be concentrated at the edge of the universe. Consequently the difference between the Casimir energy and dark energy is the difference between local and global as well as two sided and one sided boundary conditions [120] -[127] .
8. How to Build a Nano Casimir-Dark Energy Reactor
From the preceding discussion it is an inescapable conclusion that we could build a nano universe using nano technology and that such a universe will constitute a unit cell of a nano Casimir-dark energy reactor [94] [96] [120] from which we can extract an infinite amount of clean energy using empty spacetime as our fuel.
To start we can use a large amount of C60 Fullerene [7] nano particles which are the smallest dodecahedron [7] known to exist at present. There are many reasons to suspect that the universe geometry and topology resembles that of a dodecahedron so that each C60 particle is an approximately universe prototype geometrically and topologically speaking [7] . Each two faces of the C60 powder will act as a Casimir cell and the complexity of the heap will produce an artificial local high dimensionality for which Dvoretzky’s theorem applies [140] . Adding a large number of these artificial nano universes we end up with a macroscopic multiverse from which energy can in principle be extracted from its most outer surface. The rest is technological details. However we are more than aware that the devil lies in the detail. Nevertheless all that we can say at this point is that we will use in principle the same technology used to minimize the usually harmful effects of the Casimir effect on nano devices only this time in a reversed fashion, i.e. trying to maximise these effects rather than minimizing it [120] - [127] .
9. A Set Theoretical Resolution of the Black Hole Information Paradox
We started by discussing black holes, then moved from there to Casimir energy, dark energy and nano reactors [140] . With the benefit of hindsight let us see what the connection is between these seemingly very different problems. Maybe it is good for a deep understanding of the problem at hand to ask oneself can we really solve a mind teaser like the information paradox without knowing really what space is, what time is and worse still, what the word nothingness means. The present author admits that he thought that this is not possible and that was exactly his point of departure. First of all totally empty space is not nothing but something substantial even without any fluctuation or pair creation and annihilation. Empty spacetime is a multidimensional empty set. The empty set is far from being nothing. As soon as you mention the word set then the word nothing is not there. Insubstantial nothingness is not even a set. The border line is the totally empty set given by 

10. Conclusion
Actual empty spacetime is far from being nothing and is a multi-dimensional empty set, which is a substantial something. This spacetime is pointless and what appears to be a point is, upon magnification, a complete random Cantor set. In such spacetime a black hole will always have a non-zero surface area no matter how small it shrinks and will never vanish and have a zero surface area. In such a situation, and by a well known brilliant theorem due to the great late A. Dvoretzky who was at a time the President of the Wiseman Institute, at least 95.5% of the information of a black hole will not be lost. The situation is analogous to that of the ordinary and the dark energy of the universe and could be used as a guiding principle in the design of a nano Casimir-dark energy reactor. In the end analysis we think that our inability to give a waterproof definition to the words point, line and so on coupled with mildly ignoring the impact of nonlinear dynamics, chaos and fractals on fundamental quantum physics contributes to a delay of the development of black hole research and related subjects. We hope the present work has at a minimum helped positively in this direction.
Cite this paper
Mohamed S.El Naschie, (2015) A Resolution of the Black Hole Information Paradox via Transfinite Set Theory. World Journal of Condensed Matter Physics,05,249-260. doi: 10.4236/wjcmp.2015.54026
References
- 1. Marek-Crnjac, L. (2013) Cantorian Space-Time Theory: The Physics of Empty Sets in Connection with Quantum Entanglement and Dark Energy. Lambert Academic Publishing, Saarbrucken.
- 2. El Naschie, M.S. (2015) Quantum Fractals and the Casimir-Dark Energy Duality—The Road to a Clean Quantum Energy Nano Reactor. Journal of Modern Physics, 6, 1321-1333.
http://dx.doi.org/10.4236/jmp.2015.69137 - 3. El Naschie, M.S. (1998) Some Tentative Proposals for the Experimental Verification of Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 9, 143-144.
http://dx.doi.org/10.1016/S0960-0779(97)00175-6 - 4. Kumar Chattaraj, P. (2011) Quantum Trajectories. CRC Press, Taylor & Francis Group, Boca Raton.
- 5. El Naschie, M.S. (1998) The Fractal Dimension of Spacetime—Remarks on Theoretical Derivation and Experimental Verification. Chaos, Solitons & Fractals, 9, 1211-1217.
http://dx.doi.org/10.1016/S0960-0779(97)00194-X - 6. Bondi, S.H. (1964) Relativity and the Commonsense. A New Approach to Einstein. Heinemann, London.
- 7. Penrose, R. (2004) The Road to Reality. A Complete Guide to the Laws of the Universe. Jonathan Cape, London.
- 8. Okun, L.B. (2009) Energy and Mass in Relativity Theory. World Scientific, Singapore.
- 9. Rindler, W. (2004) Relativity (Special, General and Cosmological). Oxford University Press, Oxford.
- 10. El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic ‘t Hooft-Veltman-Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221.
http://dx.doi.org/10.4236/wjnst.2014.44027 - 11. Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145.
http://dx.doi.org/10.4236/ojm.2013.34020 - 12. Marek-Crnjac, L. and He, J.-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471.
http://dx.doi.org/10.4236/ijaa.2013.34053 - 13. Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436.
http://dx.doi.org/10.4236/jmp.2014.515144 - 14. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
http://dx.doi.org/10.4236/jqis.2011.12007 - 15. El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26.
http://dx.doi.org/10.4236/jqis.2013.31006 - 16. El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54.
http://dx.doi.org/10.4236/ijmnta.2013.21005 - 17. El Naschie, M.S. (2013) Quantum Entanglement: Where Dark Energy and Negative Gravity plus Accelerated Expansion of the Universe Comes from. Journal of Quantum Information Science, 3, 57-77.
http://dx.doi.org/10.4236/jqis.2013.32011 - 18. El Naschie, M.S. (2013) A Fractal Menger Sponge Space-Time Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy. International Journal of Modern Nonlinear Theory and Application, 2, 107-121.
http://dx.doi.org/10.4236/ijmnta.2013.22014 - 19. El Naschie, M.S. (2013) The Hydrogen Atom Fractal Spectra, the Missing Dark Energy of the Cosmos and Their Hardy Quantum Entanglement. International Journal of Modern Nonlinear Theory and Application, 2, 167-169.
http://dx.doi.org/10.4236/ijmnta.2013.23023 - 20. El Naschie, M.S. (2013) A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy. International Journal of Astronomy and Astrophysics, 3, 483-493.
http://dx.doi.org/10.4236/ijaa.2013.34056 - 21. El Naschie, M.S. (2013) What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy and Astrophysics, 3, 205-211.
http://dx.doi.org/10.4236/ijaa.2013.33024 - 22. El Naschie, M.S. (2013) The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling of the Planck Scale. Open Journal of Microphysics, 3, 64-70.
http://dx.doi.org/10.4236/ojm.2013.33012 - 23. El Naschie, M.S. (2013) From Yang-Mills Photon in Curved Spacetime to Dark Energy Density. Journal of Quantum Information Science, 3, 121-126.
http://dx.doi.org/10.4236/jqis.2013.34016 - 24. El Naschie, M.S. (2014) Calculating the Exact Experimental Density of the Dark Energy in the Cosmos Assuming a Fractal Speed of Light. International Journal of Modern Nonlinear Theory and Application, 3, 1-5.
http://dx.doi.org/10.4236/ijmnta.2014.31001 - 25. El Naschie, M.S. (2014) Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity. World Journal of Mechanics, 4, 153-156.
http://dx.doi.org/10.4236/wjm.2014.46017 - 26. El Naschie, M.S. (2014) Capillary Surface Energy Elucidation of the Cosmic Dark Energy—Ordinary Energy Duality. Open Journal of Fluid Dynamics, 4, 15-17.
http://dx.doi.org/10.4236/ojfd.2014.41002 - 27. El Naschie, M.S. (2014) Einstein’s General Relativity and Pure Gravity in a Cosserat and De Sitter-Witten Spacetime Setting as the Explanation of Dark Energy and Cosmic Accelerated Expansion. International Journal of Astronomy and Astrophysics, 4, 332-339.
http://dx.doi.org/10.4236/ijaa.2014.42027 - 28. El Naschie, M.S. (2014) Electromagnetic—Pure Gravity Connection via Hardy’s Quantum Entanglement. Journal of Electromagnetic Analysis and Applications, 6, 233-237.
http://dx.doi.org/10.4236/jemaa.2014.69023 - 29. El Naschie, M.S. (2014) Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91.
http://dx.doi.org/10.4236/jqis.2014.42008 - 30. El Naschie, M.S. (2014) Entanglement of E8E8 Exceptional Lie Symmetry Group Dark Energy, Einstein’s Maximal Total Energy and the Hartle-Hawking No Boundary Proposal as the Explanation for Dark Energy. World Journal of Condensed Matter Physics, 4, 74-77.
http://dx.doi.org/10.4236/wjcmp.2014.42011 - 31. El Naschie, M.S. (2014) The Meta Energy of Dark Energy. Open Journal of Philosophy, 4, 157-159.
http://dx.doi.org/10.4236/ojpp.2014.42022 - 32. El Naschie, M.S. (2014) Pinched Material Einstein Space-Time Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90.
http://dx.doi.org/10.4236/ijaa.2014.41009 - 33. El Naschie, M.S. (2014) From Chern-Simon, Holography and Scale Relativity to Dark Energy. Journal of Applied Mathematics and Physics, 2, 634-638.
http://dx.doi.org/10.4236/jamp.2014.27069 - 34. El Naschie, M.S. (2014) Why E Is Not Equal to mc2. Journal of Modern Physics, 5, 743-750.
http://dx.doi.org/10.4236/jmp.2014.59084 - 35. El Naschie, M.S. (2013) Nash Embedding of Witten’s M-Theory and the Hawking-Hartle Quantum Wave of Dark Energy. Journal of Modern Physics, 4, 1417-1428.
http://dx.doi.org/10.4236/jmp.2013.410170 - 36. El Naschie, M.S. (2013) Dark Energy from Kaluza-Klein Spacetime and Noether’s Theorem via Lagrangian Multiplier Method. Journal of Modern Physics, 4, 757-760.
http://dx.doi.org/10.4236/jmp.2013.46103 - 37. El Naschie, M.S. (2013) The Hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy. Journal of Modern Physics, 4, 354-356.
http://dx.doi.org/10.4236/jmp.2013.43049 - 38. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 39. El Naschie, M.S. (2014) From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
http://dx.doi.org/10.4236/jamp.2014.28088 - 40. He, J.-H. and Marek-Crnjac, L. (2013) Mohamed El Naschie’s Revision of Albert Einstein’s E = m0c2: A Definite Resolution of the Mystery of the Missing Dark Energy of the Cosmos. International Journal of Modern Nonlinear Theory and Application, 2, 55-59.
http://dx.doi.org/10.4236/ijmnta.2013.21006 - 41. El Naschie, M.S. and Marek-Crnjac, L. (2012) Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity. International Journal of Modern Nonlinear Theory and Application, 1, 118-124.
http://dx.doi.org/10.4236/ijmnta.2012.14018 - 42. El Naschie, M.S. and Helal, A. (2013) Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343.
http://dx.doi.org/10.4236/ijaa.2013.33037 - 43. Marek-Crnjac, L. and El Naschie, M.S. (2013) Chaotic Fractal Tiling for the Missing Dark Energy and Veneziano Model. Applied Mathematics, 4, 22-29.
http://dx.doi.org/10.4236/am.2013.411A2005 - 44. Marek-Crnjac, L. and El Naschie, M.S. (2013) Quantum Gravity and Dark Energy Using Fractal Planck Scaling. Journal of Modern Physics, 4, 31-38.
http://dx.doi.org/10.4236/jmp.2013.411A1005 - 45. Auffray, J.P. (2015) E-Infinity, the Zero Set, Absolute Space and Photon Spin. Journal of Modern Physics, 6, 536-545.
http://dx.doi.org/10.4236/jmp.2015.65058 - 46. El Naschie, M.S., Olsen, S., He, J.H., Nada, S., Marek-Crnjac, L. and Helal, A. (2012) On the Need for Fractal Logic in High Energy Quantum Physics. International Journal of Modern Nonlinear Theory and Application, 1, 84-92.
http://dx.doi.org/10.4236/ijmnta.2012.13012 - 47. El Naschie, M.S., Marek-Crnjac, L., Helal, M.A. and He, J.-H. (2014) A Topological Magueijo-Smolin Varying Speed of Light Theory, the Accelerated Cosmic Expansion and the Dark Energy of Pure Gravity. Applied Mathematics, 5, 1780-1790.
http://dx.doi.org/10.4236/am.2014.512171 - 48. El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and ‘t Hooft’s 4-ε Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37.
http://dx.doi.org/10.11648/j.ajaa.20140203.12 - 49. El Naschie, M.S. (2014) Hardy’s Entanglement as the Ultimate Explanation for the Observed Cosmic Dark Energy and Accelerated Expansion. International Journal of High Energy Physics, 1, 13-17.
http://dx.doi.org/10.11648/j.ijhep.20140102.11 - 50. El Naschie, M.S. (2014) Deriving E = mc2/22 of Einstein’s Ordinary Quantum Relativity Energy Density from the Lie Symmetry Group SO(10) of Grand Unification of All Fundamental Forces and without Quantum Mechanics. American Journal of Mechanics & Applications, 2, 6-9.
http://dx.doi.org/10.11648/j.ajma.20140202.11 - 51. El Naschie, M.S. (2014) Cosserat-Cartan Modification of Einstein-Riemann Relativity and Cosmic Dark Energy Density. American Journal of Modern Physics, 3, 82-87.
http://dx.doi.org/10.11648/j.ajmp.20140302.17 - 52. El Naschie, M.S. (2014) Asymptotically Safe Pure Gravity as the Source of Dark Energy of the Vacuum. International Journal of Astrophysics and Space Science, 2, 12-15.
http://dx.doi.org/10.11648/j.ijass.20140201.13 - 53. El Naschie, M.S. (2014) Logarithmic Running of ‘t Hooft-Polyakov Monopole to Dark Energy. International Journal of High Energy Physics, 1, 1-5.
http://dx.doi.org/10.11648/j.ijhep.20140101.11 - 54. El Naschie, M.S. (2013) Experimentally Based Theoretical Arguments that Unruh’s Temperature, Hawking’s Vacuum Fluctuation and Rindler’s Wedge Are Physically Real. American Journal of Modern Physics, 2, 357-361.
http://dx.doi.org/10.11648/j.ajmp.20130206.23 - 55. Marek-Crnjac, L. (2013) Modification of Einstein’s E = mc2 to E = (1/22)mc2. American Journal of Modern Physics, 2, 255-263.
http://dx.doi.org/10.11648/j.ajmp.20130205.14 - 56. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.
http://dx.doi.org/10.1134/S0202289313030031 - 57. El Naschie, M.S. (2013) Determining the Missing Dark Energy Density of the Cosmos from a Light Cone Exact Relativistic Analysis. Journal of Physics, 2, 19-25.
- 58. El Naschie, M.S. (2013) The Quantum Entanglement behind the Missing Dark Energy. Journal of Modern Physics and Applications, 2, 88-96.
- 59. El Naschie, M.S. (2014) Dark Energy via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
- 60. El Naschie, M.S. (2014) Rindler Space Derivation of Dark Energy. Journal of Modern Physics Applications, 6, 1-10.
- 61. Tang, W., Li, Y., Kong, H.Y. and El Naschie, M.S. (2014) From Nonlocal Elasticity to Nonlocal Spacetime and Nano Science. Bubbfil Nanotechnology, 1, 3-12.
- 62. El Naschie, M.S. (2014) To Dark Energy Theory from a Cosserat-Like Model of Spacetime. Problems of Nonlinear Analysis in Engineering Systems, 20, 79-98.
- 63. El Naschie, M.S. (2012) Revising Einstein’s E = mc2; A Theoretical Resolution of the Mystery of Dark Energy. Proceedings of the Fourth Arab International Conference in Physics and Material Science, Alexandria, 1-3 October 2012, 1.
- 64. Ball, K.M. (1991) Volume Ratios and a Reverse Isoperimetric Inequality. Journal of London Mathematical Society, 44, 351-359.
http://dx.doi.org/10.1112/jlms/s2-44.2.351 - 65. Pisier, G. (1989) The Volume of Convex Bodies and Banach Space Geometry. Tracts in Math 94, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/cbo9780511662454 - 66. Kasin, B.S. (1977) The Width of Certain Finite-Dimensional Sets and Classes of Smooth Functions. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 41, 334-351. (In Russian)
- 67. Guedon, O. (2013) Concentration Phenomena in High Dimensional Geometry.
http://arxiv.org/abs/1310.1204 - 68. He, J.-H. (2013) Special Issue on Recent Developments on Dark Energy and Dark Matter. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 3, 1-2.
- 69. He, J.-H. and El Naschie, M.S. (2012) On the Monadic Nature of Quantum Gravity as a Highly Structured Golden Ring, Spaces and Spectra. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 94-98.
- 70. El Naschie, M.S. (2012) Towards a General Transfinite Set Theory for Quantum Mechanics. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 135-142.
- 71. El Naschie, M.S., He, J.-H., Nada, S., Marek-Crnjac, L. and Helal, M. (2012) Golden Mean Computer for High Energy Physics. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 80-92.
- 72. El Naschie, M.S. (2012) The Minus One Connection of Relativity, Quantum Mechanics and Set Theory. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 131-134.
- 73. El Naschie, M.S. (2015) Dark Energy and Its Cosmic Density from Einstein’s Relativity and Gauge Fields Renormalization Leading to the Possibility of a New ‘t Hooft Quasi Particle. The Open Journal of Astronomy, 8, 1-17.
http://dx.doi.org/10.2174/1874381101508010001 - 74. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 75. El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646.
http://dx.doi.org/10.1016/j.chaos.2008.09.059 - 76. Connes, A. (1994) Noncommutative Geometry. Academic Press, San Diego.
- 77. Krantz, S.G. and Parks, H.R. (2008) Geometric Integration Theory. Birkhauser, Boston.
http://dx.doi.org/10.1007/978-0-8176-4679-0 - 78. El Naschie, M.S. (1997) Remarks on Super Strings, Fractal Gravity, Nagasawa’s Diffusion and Cantorian Spacetime. Chaos, Solitons & Fractals, 8, 1873-1886.
http://dx.doi.org/10.1016/S0960-0779(97)00124-0 - 79. El Naschie, M.S. (1997) Introduction to Nonlinear Dynamics, General Relativity and the Quantum—The Uneven Flow of Fractal Time. Chaos, Solitons & Fractals, 8, vii-x.
http://dx.doi.org/10.1016/S0960-0779(97)88695-X - 80. El Naschie, M.S. (1999) Hyper-Dimensional Geometry and the Nature of Physical Spacetime. Chaos, Solitons & Fractals, 10, 155-158.
http://dx.doi.org/10.1016/S0960-0779(98)00235-5 - 81. El Naschie, M.S. (2012) E-Infinity—High Energy Communications Nos. 1-90. April 2010 to December 2012.
- 82. Chen, N.X. (2010) Möbius Inversion in Physics. World Scientific, Singapore.
- 83. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.
http://dx.doi.org/10.1007/s10773-014-2123-8 - 84. El Naschie, M.S. (2001) On Twistors in Cantorian E-Infinity Space. Chaos, Solitons & Fractals, 12, 741-746.
http://dx.doi.org/10.1016/S0960-0779(00)00193-4 - 85. Rössler, O.E. (1998) Endophysics. World Scientific, Singapore.
http://dx.doi.org/10.1142/3183 - 86. El Naschie, M.S. (2001) On a General Theory for Quantum Gravity. In: Diebner, H., Druckrey, T. and Weibel, P., Eds., Science of the Interface, Genista Verlag, Tübingen.
- 87. Li, M. (2004) A Model of Holographic Dark Energy. Physics Letters B, 603, 1-5.
http://dx.doi.org/10.1016/j.physletb.2004.10.014 - 88. El Naschie, M.S. (2006) Holographic Dimensional Reduction. Center Manifold Theorem and E-Infinity. Chaos, Solitons & Fractals, 29, 816-822.
http://dx.doi.org/10.1016/j.chaos.2006.01.013 - 89. Balachandran, A.P., Kürkcüoglu, S. and Vaidya, S. (2007) Lectures on Fuzzy and Fuzzy Susy Physics. World Scientific, Singapore.
- 90. Bahcall, J., Piran, T. and Weinberg, S., Eds. (2004) Dark Matter in the Universe. World Scientific, Singapore.
- 91. Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observations. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/cbo9780511750823 - 92. Ruiz-Lapuente, P. (2010) Dark Energy, Observational and Theoretical Approaches. Cambridge University Press, Cambridge.
- 93. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entangled Origin. Journal of Quantum Information Science, 4, 284-291.
http://dx.doi.org/10.4236/jqis.2014.44023 - 94. El Naschie, M.S. (2014) Casimir-Like Energy as a Double Eigenvalue of Quantumly Entangled System Leading to the Missing Dark Energy Density of the Cosmos. International Journal of High Energy Physics, 1, 55-63.
http://dx.doi.org/10.11648/j.ijhep.20140105.11 - 95. Perlmutter, S., et al., Supernova Cosmology Project Collaboration (1999) Measurements of Omega and Lambda from 42 High Redshift Supernova. Astrophysics Journal, 517, 565-585.
http://dx.doi.org/10.1086/307221 - 96. El Naschie, M.S. (2015) On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Science, 5, 313-324.
http://dx.doi.org/10.4236/ojapps.2015.57032 - 97. Kodiyalam, V. and Sunder, V.S. (2001) Topological Quantum Field Theories from Subfactors. Chapman & Hall/CRC, London.
- 98. El Naschie, M.S. (2005) A Few Hints and Some Theorem about Witten’s M Theory and T-Duality. Chaos, Solitons & Fractals, 25, 545-548.
http://dx.doi.org/10.1016/j.chaos.2005.01.009 - 99. Marek-Crnjac, L., El Naschie, M.S. and He, J.-H. (2013) Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology. International Journal of Modern Nonlinear Theory and Application, 2, 78-88.
http://dx.doi.org/10.4236/ijmnta.2013.21a010 - 100. Yau, S.T. and Nadis, S. (2010) The Shape of Inner Space. Basic Book, Perseus Group, New York.
- 101. Bell, J.S. (1991) Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge.
- 102. Rindler, W. (1991) Introduction to Special Relativity. Oxford Science Publications, Oxford.
- 103. El Naschie, M.S. (2007) Hilbert Space, Poincaré Dodecahedron and Golden Mean Transfiniteness. Chaos, Solitons & Fractals, 31, 787-793.
http://dx.doi.org/10.1016/j.chaos.2006.06.003 - 104. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
http://dx.doi.org/10.4236/jqis.2011.12007 - 105. Hardy, L. (1993) Nonlocality of Two Particles without Inequalities for Almost All Entangled States. Physical Review Letters, 71, 1665-1668.
http://dx.doi.org/10.1103/PhysRevLett.71.1665 - 106. Mermin, D. (1994) Quantum Mysteries Refined. American Journal of Physics, 62, 880-887.
http://dx.doi.org/10.1119/1.17733 - 107. Addison, P.S. (1997) Fractals and Chaos: An Illustrated Course. Institute of Physics, Bristol.
http://dx.doi.org/10.1201/9780849384431 - 108. Ruelle, D. (1991) Chance and Chaos. Princeton University Press, Princeton.
- 109. Graham, L. and Kantor, J.-M. (2009) Naming Infinity. The Belknap Press of Harvard University Press, Cambridge, MA and London.
- 110. Ott, E. (1993) Chaos in Dynamical Systems. Cambridge University Press, Cambridge.
- 111. Kapitaniak, T., Ed. (1992) Chaotic Oscillators (Theory and Applications). World Scientific, Singapore.
http://dx.doi.org/10.1142/9789814360258 - 112. Casati, G., Guarneri, I. and Smilansky, U. (1993) Quantum Chaos. North Holland, Amsterdam.
- 113. Kim, Y.S. and Noz, M.E. (1991) Phase Space Picture of Quantum Mechanics. World Scientific, Singapore.
http://dx.doi.org/10.1142/1197 - 114. Fried, H.M. (2014) Modern Functional Quantum Field Theory. World Scientific, Singapore.
http://dx.doi.org/10.1142/8544 - 115. El Naschie, M.S. (1995) Young Double-Slit Experiment, Heisenberg Uncertainty Principle and Correlation in Cantorian Spacetime. In: El Naschie, M.S., Rössler, O.E. and Prigogine, I., Eds., Quantum Mechanics, Diffusion and Chaotic Fractals, Pergamon Press/Elsevier, Oxford, 93-100.
- 116. El Naschie, M.S. (1995) Iterated Function System, Information and the Two-Slit Experiment of Quantum Mechanics. In: El Naschie, M.S., Rössler, O.E. and Prigogine, I., Eds., Quantum Mechanics, Diffusion and Chaotic Fractals, Pergamon Press/Elsevier, Oxford, 185-189.
- 117. El Naschie, M.S. (1995) Quantum Measurement, Information, Diffusion and Cantorian Geodesic. In: El Naschie, M.S., Rössler, O.E. and Prigogine, I., Eds., Quantum Mechanics, Diffusion and Chaotic Fractals, Pergamon Press/Elsevier, Oxford, 191-205.
- 118. El Naschie, M.S. (2015) Hubble Scale Dark Energy Meets Nano Scale Casimir Energy and the Rational of Their T-Duality and Mirror Symmetry Equivalence. World Journal of Nano Science and Engineering, 5, 57-67.
http://dx.doi.org/10.4236/wjnse.2015.53008 - 119. El Naschie, M.S. (2015) An Exact Mathematical Picture of Quantum Spacetime. Advances in Pure Mathematics, 5, 560-570.
http://dx.doi.org/10.4236/apm.2015.59052 - 120. El Naschie, M.S. (2015) From Fusion Algebra to Cold Fusion or from Pure Reason to Pragmatism. Open Journal of Philosophy, 5, 319-326.
http://dx.doi.org/10.4236/ojpp.2015.56040 - 121. El Naschie, M.S. (2015) Casimir-Dark Energy Nano Reactor Design Proposal Based on Fractals. International Journal of Innovation is Science and Mathematics, 3, 187-194.
- 122. Thom, R. (1975) Structural Stability and Morphogenesis. W.A. Benjamin Inc., London.
- 123. El Naschie, M.S. (2003) The VAK of Vacuum Fluctuation, Spontaneous Self Organization and Complexity Theory Interpretation of High Energy Particle Physics and the Mass Spectrum. Chaos, Solitons & Fractals, 18, 401-420.
http://dx.doi.org/10.1016/S0960-0779(03)00098-5 - 124. El Naschie, M.S. (2003) VAK, Vacuum Fluctuation and the Mass Spectrum of High Energy Physics. Chaos, Solitons & Fractals, 30, 579-605.
http://dx.doi.org/10.1016/s0960-0779(02)00684-7 - 125. El Naschie, M.S. (1991) Stress, Stability and Chaos in Structural Engineering: An Energy Approach. McGraw Hill, London.
- 126. Thompson, J.M.T. and Hunt, G. (1973) A General Theory of Elastic Stability. John Wiley, London.
- 127. El Naschie, M.S. (2015) A Casimir Dark Energy Nano Reactor Design—Phase One. Natural Science, 7, 287-298.
http://dx.doi.org/10.4236/ns.2015.76032 - 128. El Naschie, M.S. (2016) Cosserat-Cartan and de Sitter-Witten Spacetime Setting for Dark Energy. Quantum Matter, 5, 1-4.
http://dx.doi.org/10.1166/qm.2016.1247 - 129. El Naschie, M.S. (2015) The Cantorian Monadic Plasma behind the Zero Point Vacuum Spacetime Energy. American Journal of Nano Research & Application, 3, 66-70.
- 130. El Naschie, M.S. (2015) A Nonperturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Science, 5, 313-324.
http://dx.doi.org/10.4236/ojapps.2015.57032 - 131. Ho, M.-W., El Naschie, M.S. and Giuseppe Vitello, M.W. (2015) Is Spacetime Fractal and Quantum Coherent in the Golden Mean? Global Journal of Science Frontier Research, 15, 61-80.
- 132. El Naschie, M.S. (1998) Von Neumann Geometry and E-Infinity Quantum Spacetime. Chaos, Solitons & Fractals, 9, 2023-2030.
- 133. Moskowitz, C. (2015) Stephen Hawking Hasn’t Solved the Black Hole Paradox Just Yet. Scientific American, August 27, 2015.
- 134. Feltman, R. (2015) Stephen Hawking Believes He’s Solved a Huge Mystery about Black Holes. The Washington Post, August 25, 2015.
- 135. Rincon, P. (2015) Hawking: Black Holes Store Information. BBC News, Science & Environment, 26 August, 2015.
- 136. Susskind, L. and Lindesay, J. (2005) Black Holes, Information and the String Theory Revolution. World Scientific, Singapore.
- 137. Susskind, L. (2008) The Black Hole Wave. Back Bay Books, New York.
- 138. El Naschie, M.S. (2006) Fractal Black Holes and Information. Chaos, Solitons & Fractals, 29, 23-35.
http://dx.doi.org/10.1016/j.chaos.2005.11.079 - 139. ‘t Hooft, G. (1985) On the Quantum Structure of a Black Hole. Nuclear Physics B, 256, 727-745.
http://dx.doi.org/10.1016/0550-3213(85)90418-3 - 140. El Naschie, M.S. (2014) The Measure Concentration of Convex Geometry in a Quasi Banach Spacetime behind the Supposedly Missing Dark Energy of the Cosmos. American Journal of Astronomy & Astrophysics, 2, 72-77.
http://dx.doi.org/10.11648/j.ajaa.20140206.13


