Received 25 April 2015; accepted 24 July 2015; published 27 July 2015

ABSTRACT

This work focuses on the study of mathematical aspects of upper critical magnetic field of superconducting HoMo₆Se₈. At zero external magnetic field, HoMo₆Se₈ was found to undergo a transition from the normal state to the superconducting state at 5.6 K and returned to a normal but magnetically ordered state between the temperature range of 0.3 K and 0.53 K. The main objective of this work is to show the temperature dependence of the upper critical magnetic field of superconducting HoMo₆Se₈ by using the Ginzburg-Landau (GL) phenomenological Equation. We found the direct relationship between the GL coherence length (ξ_GL) and penetration depth (λ_GL) with temperature. From the GL Equations and the results obtained for the GL coherence length, the expression for upper critical magnetic field (H_c2) is obtained for the superconducting HoMo₆Se₈. The result is plotted as a function of temperature. The graph shows the linear dependence of upper critical magnetic field (H_c2) with temperature (T) and our finding is in agreement with experimental observations.

Keywords:

Ginzburg-Landau Equation, Upper Critical Magnetic Field, HoMo₆Se₈

1. Introduction

Superconductivity is a phenomenon that occurs at very low temperatures. Every superconductor has a transition temperature (T_c) below which it superconducts and above which it is a normal metal [1] . In the superconducting state, the material has no electrical resistance and thus conducts electricity without losses. On the other hand, in the normal state, the material does have resistance and the flow of electric current accompanies with the development of heat and the dissipation of energy [1] .

The era of low-temperature physics began in 1908 when the Dutch physicist Heike Kamerlingh Onnes first liquefied helium which boiled at 4.2 K at standard pressure. Three years later, in 1911, Kamerlingh Onnes discovered the phenomenon of superconductivity while studying the resistivity of metals at low temperatures [1] .

Most of the fundamental properties of superconductors vary from material to material. The superconducting state, as any state of matter, has its own basic properties. So, any superconductor independent of the mechanism of superconductivity and the material will exhibit these properties. The basic properties of the superconducting state are zero resistance, Meissner effect, magnetic flux quantization, Josephson effects, the BCS theory, Cooper pair, appearance of an energy gap in elementary excitation energy spectrum, Isotope effect and the proximity effect. Every superconducting transition is marked by a jump in specific heat. In the mixed state, the behavior of type-II superconductors has the same pattern [3] [4] .

HoMo₆Se₈ compound is building blocks of the Chevrel-phase crystal structure [5] . The discovery in 1984 of the new superconducting HoMo₆Se₈ gave rise to a renewed interest in the interplay of magnetism and superconductivity. From the experimental results, a magnetic phase transition (T_n = 0.53 K) to a long-period magnetic states has been observed via neutron scattering in the superconductor HoMo₆Se₈ (T_c = 5.6 K) [6] . The characteristic wave vector (q_c) is strongly temperature dependent and there is no observation of higher-order satellites.

The rare occurrence of ferromagnetism, as found in HoMo₆Se₈ and HoMo₆Se₈, revealed the strongly competitive nature of these two cooperative phenomena in the form of long-wavelength at low oscillatory magnetic temperature (<1 K) and a ferromagnetic lock-in transition that quenched the superconductivity. No sign of reentrant behavior (in zero field) was observed down to 0.04 K [6] [7] . Ternary rare-earth superconductors which display a propensity for ferromagnetism have received considerable experimental as well as theoretical attention recently. In the case of the new superconductors, HoMo₆Se₈ was observed despite the presence of the holmium moment of the rare earth ion in each unit cell. These compounds did not destroy the property of superconductivity at low temperature. In HoMo₆Se₈, the domain coexistence phase survives till T = 0.3 K (the exchange interaction is weaker and the coexistence persists down to T = 0.3 K) [8] . In addition to the superconducting and ferromagnetic domains, a coexistence region is observed in HoMo₆Se₈ in which the superconducting state coexists with a long range modulated magnetic order in a narrow region above the reentrant temperature T_c2.

The upper critical magnetic field is a very important magnetic superconductivity parameter. Therefore, starting from its discovery as a superconducting material, experiments are carried out to analysis the upper critical magnetic field (H_c2) of HoMo₆Se₈.

According to magnetization measurements, on both poly and single crystalline samples of the ferromagnetic superconducting HoMo₆Se₈, the upper critical magnetic field is a turning point from the superconducting state to the normal state. The first-order phase transition is the inter changing point of the superconducting state to the normal state observed when the external field H is applied parallel to the magnetically easy axis (a axis of the hexagonal-rhombohedral crystal lattice structure).

The critical magnetic field in type-I superconductor is the inter changing point of superconducting state into

normal state. From Maxwell’s Equation, 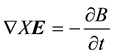, when the magnetic field is frozen, the field is expelled

from the interior of the superconductors, otherwise superconductivity will be destroyed by a critical magnetic field (H_c), such that

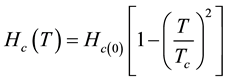(1)

Equation (1) yields the expression of thermodynamic critical magnetic field 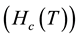[9] .

2. Mathematical Formulations to Find the Upper Critical Magnetic Field of HoMo₆Se₈

2.1. The Basic Ginzburg-Landau Theory

Ginzburg-Landau (GL) theory is a mathematical theory used to describe superconductivity. Ginzburg-Landau (GL) theory is used to explain the difference between Type-I and Type-II superconductors and enables the calculation of two critical magnetic fields H_c1 and H_c2 [10] . Ginzburg-Landau theory was derived from the BCS microscopic theory by Lev Gorkov, showing that it also appears in some limit of microscopic theory and applying microscopic interpretation of all its parameters.

The basic postulate of GL is that if ψ is small and varies slowly in space, the free-energy density 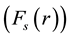can be expanded in a series of the form:

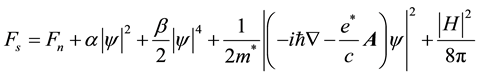(2)

where α and β are phenomenological parameters, (β is positive and the sign of α is temperature dependent), 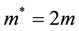is an effective mass, 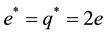is the charge of an electron, 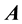is the magnetic vector potential and 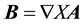is the magnetic field [5] [10] .

If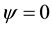, Equation (2) reduces to the free energy of the normal state;.

Now, by minimizing the free energy with respect to fluctuations in the order parameter and the vector potential, one arrives at the Ginzburg-Landau Equations given by:

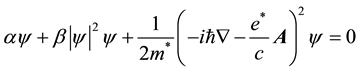(3)

The current density from the Hamilton’s energy of particles is given by;

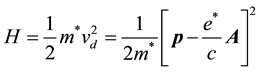
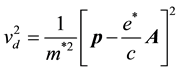
where

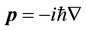
where

(4)

(5)

where is supercurrent density.

Equation (3) determines the order parameter ψ based on the applied magnetic field and Equation (5) yields the superconducting current density. The Ginzburg-Landau Equation provides complete information about the superconducting state that gives the spatial distribution of the Cooper pair density taking into account a possible variation in their concentration, where as describes the local distribution of the magnetic field in the superconductor.

In the absence of external magnetic field (at free surface), there will not be superconducting current(current flow) and the Equation for ψ becomes:

(6)

This Equation has a trivial solution ψ = 0 and it corresponds to normal state of. Below superconducting transition temperature (T_c), Equation (6) is expected to have a non-trivial solution (i.e.) and the Equation can be rearranged into:

(7)

If the second part of Equation (3) is positive, then there is a non zero solution for ψ and this can be achieved

by assuming the temperature dependence of α such that with and. For, the expression is positive and the second part of Equation (3) is negative and only ψ = 0

solves the Ginzburg-Landau Equation. For, the second part of Equation (3) is positive and there is a non-trivial solution for ψ. Thus Equation (7) can be expressed as:

(8)

Equation (8) yields Ginzburg Landau order parameter [5] [11] .

2.2. Calculation of Ginzburg-Landau Coherence Length

The Ginzbrug-Landau coherence length (ξ_GL) is a measure of the distance in the superconducting electron concentration that can not change drastically in a spatially-varying magnetic field. The Ginzbrug-Landau coherence length (ξ_GL) is a temperature-dependent as well as a material dependent quantity. In the case of absence of the magnetic vector potential, Equation (3) reduces to:

(9)

Now, let us consider a wave function that varies only in the z-direction with zero applied magnetic field. In this case, the first GL Equation is one dimensional.

i.e,

(10)

Assuming ψ is real and neglecting the term in comparison with α, Equation (10), becomes:

(11)

For the plane wave function, the solution of Equation (11) is in the form of,

(12)

Substituting the value of plane wave function into Equation (11) (in terms of), we get,

This implies that,

(13)

Solving for ξ_GL at superconducting state that means, where α is negative yields,

(14)

where, and

Equation (14) yields the GL coherence length [2] . Since α depends on temperature as, then we can conclude that coherence length is temperature dependent.

Now let us consider the cases:

Case (I), For superconducting state (T < T_c),

(15)

and

Case (II), For normal state (T > T_c),

(16)

Case (III), at T = T_c, the GL theory is not valid

Where the length ξ_GL(0) is known as the zero temperature GL coherence length.

2.3. Calculation of Ginzburg-Landau Penetration Depth

The surface current flows in a very thin layer of thickness (λ_GL) which is called the Ginzburg-Landau penetration depth [2] . The temperature and magnetic field dependence of the penetration depth appear quite naturally in Ginzburg-Landau (GL) theory. Like the London model, the GL model is independent of the underlying mechanism for superconductivity. Ginzburg-Landau theory is strictly valid only in superconducting phase boundary and is thus not generally applicable at low temperatures [2] . In the Ginzburg-Landau theory, a complex order parameter(ψ) is a function of temperature, magnetic field and the spatial coordinates [5] [10] . The total free energy per unit volume of the superconducting state in the presence of a magnetic field is minimizing this expression with respect to the first GL Equation and with respect to the current density(GL-II) Equation;

(17)

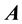
where and.

(18)

Using Equation (17), we get the expression for current density, as follows

(19)

since

(20)

Neglecting and Equation (20), becomes;

(21)

Using Maxwell’s Equation:

(22)

Taking the curl on both sides of Equation (22), we get

(23)

(24)

where, and

From Equation (22) and Equation (24), we get

(25)

(26)

Since and, we get

(27)

Therefore,

(28)

(29)

where and.

Therefore,

(30)

For

(31)

from Equation (30) [9] it follows that, the Ginzburg-Landua penetration depth (λ_GL(T)) varies as a function of temperature as:

(32)

(33)

where λ_L(0) is the London penetration at absolute zero temperature [9] .

2.4. Calculation of the Upper Critical Magnetic Field Using Ginzburg-Landau Theory

The upper critical magnetic field (UCMF) is the magnetic field which completely suppresses superconductivity in type-II superconductors. More properly, the UCMF is a function of temperature (and pressure) and if not specified absolute zero and standard pressure are implied. Supercondcting region nucleates spontaneously within a normal conductor when the applied magnetic field is decreased below a value denoted by H_c2 [8] . At the onset of superconductivity, is small and we linearize the GL Equations as follows;

(34)

Since, , and.

The upper critical magnetic field (H_c2) can be calculated by linearizing Equation (34) and substituting the value of as:

(35)

The magnetic field in a superconducting region at the onset of superconductivity is just the applied field, so that and Equation (35) becomes

(36)

where and where the eigne value of mo-

mentum crystal is.

Therefore,

(37)

Since the expression of the Hamiltonian’s energy given in Equation (37) does not depend on coordinates (y and z) the corresponding momentum components (,) are conserved.

(38)

(39)

(40)

The largest value of the magnetic field (B) for which the solution of Equation (40) of the lowest eigenvalue is given by

(41)

Let us take the smallest eigenvalues n = 0 and K_z = 0 corresponding to the highest field in which superconductivity can nucleate in the interior of a bulk sample which occurs with the upper critical magnetic field in the coefficients change of sign. From Equation (41), we have;

(42)

where is the cyclotron frequency and is given by

(43)

since, solving for, we get:

(44)

From the relation that means, and.

We obtain the expression of the temperature dependent upper critical magnetic field (),

(45)

where or and

2.5. Anisotropic Mass Tensor Model

Now, consider anisotropy in mass, by introducing the effective mass tensor to the kinetic energy term of the GL Equation (3), i.e.

(46)

where is an effective mass tensor which is given by,

Since the coherence length depends on the effective mass as, the resulting Equation is

formally identical with the Schrödinger Equation of a particle with charge, an isotropic mass tensor in a uniform magnetic field H and the energy levels that have the harmonic oscillator are given by;

(47)

Let us consider Newton’s law of motion under the influence of lorentz force

i.e.

(48)

where v is the velocity.

The upper critical magnetic field can be expressed by using cyclotron frequency with the lowest free energy;

The solution of upper critical magnetic field by applying elliptical orbits traversed with cyclotron frequency is given by,

(49)

The solution of the lowest free energy corresponds to n = 0 and by using Equation (49), we get

where θ is the angle of the magnetic field that makes with the z-axis

.

(50)

From the general expression of coherence length Equation (45) we have,

(51)

(52)

Using the expression for the flux quantization, and Equation (45), can be expressed as,

(53)

For fields parallel and perpendicular to the symmetry plane we can write Equation (53) as:

(54)

and

(55)

Equations (54) and (55) are the mathematical expressions of the upper critical magnetic field (H_c2) for fields parallel and perpendicular to the symmetry axis [4] .

3. Results and Discussion

From Equation (15), we obtained the graph that shows the relationship between the GL coherence length and temperature (T) as indicated in Figure 1.

As can be see from Figure 1, the GL coherence length increases with temperature and diverge as. has the same value with the BCS coherence length i.e. () [2] .

We have already calculated the GL penetration depth in (33), the relationship between the GL penetration depth and temperature(T) is shown in Figure 2.

From Figure 2, we observe that, the increase of the GL penetration depth with temperature (T) and generally, we observe that, the penetration depth rises asymptotically as the temperature approaches T_c. Thus, the pene- tration of field increase as the temperature approaches to T_c.

We finally determined the expression for upper critical magnetic field for superconducting HoMo₆Se₈ using the GL Equation (45) and by taking experimental data and upper critical magnetic fields for parallel and perpendicular, we plot the upper critical fields at parallel and perpendicular to the symmetry axis as shown in Figure 3 [6] [7] .

From Figure 3, we can see that, the upper critical magnetic field decreases as temperature increases and reaches to zero at the critical temperature of superconducting HoMo₆Se₈, which agrees with the experimental observations [6] . And as can be seen from $, the upper critical magnetic field (H_c2) parallel and perpendicular to the symmetry axis of superconducting HoMo₆Se₈ is inversely proportional to the GL coherence length and fits.

4. Conclusion

The aim of this research is to determine the upper critical field of superconducting HoMo₆Se₈ by using Ginzburg-Landau approach. From the calculation, the effect of coherence length, penetration depth and anisotropy in mass tensor on upper critical field are considered in our model. And finally figures are plotted by using MATLAB scripts. From the figures plotted, it can be concluded that the upper critical magnetic field of superconducting HoMo₆Se₈ is inversely related to temperature which is in agreement with experimental observations [6] .

Cite this paper

TadesseDesta,PooranSingh,GebregziabherKahsay, (2015) Study of Upper Critical Magnetic Field of Superconducting HoMo₆Se₈. World Journal of Condensed Matter Physics,05,105-117. doi: 10.4236/wjcmp.2015.53013

References