World Journal of Condensed Matter Physics
Vol.05 No.02(2015), Article ID:55287,4 pages
10.4236/wjcmp.2015.52008
Violating of the Essam-Fisher and Rushbrooke Relationships at Low Temperatures
Vladimir Udodov
Department of Theoretical Physics, Katanov Khakas State University, Abakan, Russia
Email: udododvv@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 January 2015; accepted 30 March 2015; published 1 April 2015
ABSTRACT
The Essam-Fisher and Rushbrooke relationships (1963) that connect the equilibrium critical exponents of susceptibility, specific heat and order parameter (and some other relations that follow from the scaling hypothesis) are shown to be valid only if the critical temperature TС > 0 and T → TC. For phase transitions (PT’s) with TC = 0 K these relations are proved to be of different form. This fact has been actually observed experimentally, but the reasons were not quite clear. A general formula containing the classical results as a special case is proposed. This formula is applicable to all equilibrium PT’s of any space dimension for both TC = 0 and TC > 0. The predictions of the theory are consistent with the available experimental data and do not cast any doubts upon the scaling hypothesis.
Keywords:
Essam-Fisher and Rushbrooke Relationships, The Equilibrium Critical Exponents, The Scaling Hypothesis, Low Temperatures

1. Introduction
The critical exponents and scaling hypothesis (Patashinsky and Pokrovsky (1964); Widom (1965); Domb and Hunter (1965); Kadanoff (1966)) underlying the theory of critical phenomena [1] -[5] . Essam and Fisher equality [6] and Rushbrooke inequality [7] (as the most famous inequality between critical exponents) were discovered 52 years ago and everyone believed that the relations are performed. These relations are connected with the critical exponents of the specific heat (α, α'), susceptibility (γ, γ') and the order parameter β (determining of the critical exponents see below) [1] - [7] . In 1965-1966, it was shown that under the scaling hypothesis the Essam and Fisher equality are fulfilled and the Rushbrooke inequality  reduces to equality [1]
reduces to equality [1]
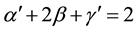 .)
.)
These results were obtained under the assumption that the critical temperature is finite TС > 0 and T→TC. However, recently quantum phase transitions (PT’s) have inspired a new interest in low-temperature thermodynamics and statistical physics [8] - [10] . For quantum PT’s the temperature of phase transition TC is zero. In this paper we show that if TС = 0 K, the classical Essam-Fisher equation and Rushbrooke inequality changes: the right-hand side equal to two, is replaced by one. Change as well, and some other equations for the critical exponents resulting from the scaling hypothesis. In this paper, we propose a general interpolation formula (generalized Essam-Fisher equality), the right side of which ranges from 2 to 1. This general formula is valid for both finite critical temperature and for the case of TС = 0 K. In the experimental measurements of the critical exponents for the PT's at low temperatures (T → 0) we can expect that the right side of these relations will be less than 2 [1] . The proposed theory can be tested for any quantum phase transitions [8] -[11] .
Even now there is evidence that these relations are broken. For example, for the magnetic transition in nickel we have [12] (within the framework of the scaling hypothesis γ = γ')
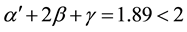 .
.
For the critical point in CO2 [12] , for example,
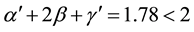 .
.
Explanations of these violations were absent apart from possible measurement errors, but everyone believed that the formulas are correct, since derived from thermodynamics. The situation is complicated by the fact that a breach of these relationships speaks about the disturbance of the scaling hypothesis [1] - [5] . Though the apparent violations of the scaling hypothesis are discussed by Aharony and Ahlers [13] , they did not consider the case of zero critical temperature.
It turns out, if TС = 0, the classic relationships [6] [7] have the different form and this may be explains the apparent violations and it can save the scaling hypothesis.
2. The Essam and Fisher Equality
First, we recall the usual derived Essam-Fisher equality. The order parameter in a weak field (or lack thereof) is proportional to [1] - [3]
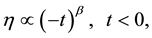 (1)
(1)
where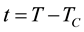 , β is order parameter critical exponent. On the other hand in a weak field h, the order parameter is [3]
, β is order parameter critical exponent. On the other hand in a weak field h, the order parameter is [3]
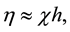 (2)
(2)
where χ?susceptibility, the critical exponent is determined by the ratio (in a weak field) [1] - [3]
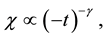 (3)
(3)
γ?the critical exponent of the susceptibility. In the field PT becomes fuzzy. If we substitute Equations (1) and (3) in Equation (2), we find blur for temperature interval of PT [3]
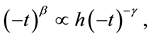 (4)
(4)
from which we obtain
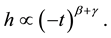 (5)
(5)
The same interval of blur can be found from the requirement that a field term of potential Gh is equal to a heat term GT [3] (G?the Gibbs potential [1] - [3] )
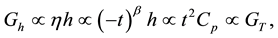 (6)
(6)
where Ср?heat capacity, for which the formula is valid in weak field [1] -[3]
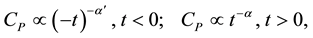 (7)
(7)
α, α'?the heat capacity critical exponents, within the framework of the scaling hypothesis α = α' [1] . Substituting Equations (5) and (7) into Equation (6) this gives
 (8)
(8)
or
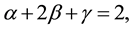 (9)
(9)
it is Essam and Fisher equality [1] [3] [6] .
Longer arguments prove Rushbrooke inequality [1] [7] , which is true for the stable states
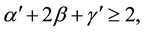 (10)
(10)
where the primed symbols correspond to the region below the PT point (at temperature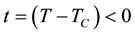 ), the order parameter critical exponent β is defined only in this area [1] -[3] . In rare cases, the asymmetric phase can be high-temperature phase [3] , then the exponent β is determined for
), the order parameter critical exponent β is defined only in this area [1] -[3] . In rare cases, the asymmetric phase can be high-temperature phase [3] , then the exponent β is determined for
3. The Case of Zero Critical Temperature
Note that the heat term has the form (6) only if TС > 0. In fact, let

We show that the heat term GT in the form shown in Equation (6) leads to incorrect results. From Equation (11) it follows that

The thermal term becomes in the form (within the framework of the scaling hypothesis

We find the entropy

and heat capacity (using Equations (12) and (14))

which contradicts Equation (7).
Let us find the right formula. Let heat term has the form

We now find b. Heat capacity is

hence we have
and

Essam and Fisher equality will take the form [14]

which differs from the standard formula (9) [1] -[3] [6] .
4. The General Case
In the general case may be offered the following interpolation formula (generalized Essam-Fisher equality)

where S-function is [14]

where positive constant n can be found either from the comparison with experiment, or from the microscopic theory. Indeed, if the TC = 0 (T > 0), then we arrive at the formula (19). If TC > 0 and T → TC, we get a classical Essam and Fisher equality (9).
Turns out, if the number n is fraction, then S-function is a nonanalitic function at a point






Now consider the case
where

Now the S-function is analytic function at a point

where

that is, the right-hand side of equality (25) can be less than 2. We obtained a principal result: the right side of the classic relationships is not a constant, but rather a function that depends on the temperature and takes the values from 1 to 2.
Finally, two equalities which follow from the scaling hypothesis [1] [3]


alter their appearance (d?the space dimension, ν?critical exponent of the correlation length). ε?critical exponent for strong field [3]

Scaling relations now take the form


r?phase transition order in the sense of Baxter R. [2] , we believe that the scaling hypothesis is performed.
It should be noted that the S-function expresses the degree of “classical” behavior. Thus, 

5. Conclusions
Thus showed that the classical Essam and Fisher equation and Rushbrooke inequality are only valid if the critical temperature TC is finite and T → TC. If the critical temperature is zero, the classic relationships change its form: on the right side instead of the deuce will be unit. Because at change of parameters critical temperature tends to zero for many quantum phase transitions, the right-hand side of these relations should be continuously varied from 2 to 1 [14] .
The real test of the results is possible for any quantum phase transitions [9] [10] as T → 0, for example for ferromagnetic Ce2.15Pd1.95In0.9 [11] , for heavy-fermions systems [15] or for superconductors [10] .
We note that the relations (19), (20), (25) are equilibrium, which implies that the right side equal to one, is unlikely to be achieved because the relaxation time (the transition to the equilibrium state) at T → TC ~ 0 tends to infinity (critical slowing). In conclusion, it must be emphasized that the results can be observed at temperatures not very low (see [12] ).
Acknowledgements
I thank S. Prosandeev and A. Levanyuk for discussions and I am grateful for discussions and the support to I. Naumov.
References
- Stanley, H.E. (1971) Introduction to Phase Transitions and Critical Phenomena. Physics Department Massachusetts Institute of Technology, Clarendon Press, Oxford.
- Baxter, R.J. (1982) Exactly Solved Models in Statistical Mechanics. Academic Press, London, New York, Sydney, Tokyo, Toronto.
- Landau, L.D. and Lifshitz, E.M. (1980) Statistical Physics. Vol. 5. 3rd Edition, Butterworth-Heinemann.
- Patashinskii, A.Z. and Pokrovskii, V.L. (1964) Second Order Phase Transitions in a Bose Fluid. Soviet physics JETP, 19, 677-691.
- Kadanoff, L.P. (1966) Scaling Laws for Ising Models near TC. Physics, 2, 263.
- Essam, J.W. and Fisher, M.E. (1963) Padé Approximant Studies of the Lattice Gas and Ising Ferromagnet below the Critical Point. Journal of Chemical Physics, 38, 802-812. http://dx.doi.org/10.1063/1.1733766
- Rushbrooke, G.S. (1963) On the Thermodynamics of the Critical Region for the Ising Problem. The Journal of Chemi- cal Physics, 39, 842. http://dx.doi.org/10.1063/1.1734338
- Rechester, A.B. (1971) Contribution to the Theory of Second-Order Phase Transitions at Low Temperatures. Soviet Physics JETP, 33, 423-430.
- Sachdev, S. (1999) Quantum Phase Transitions. Yale University, New Haven.
- Abrikosov, A.A. (1988) Fundamentals of the Theory of Metals. North-Holland, Amsterdam.
- Sereni, J.G., Giovannini, M., Goґmez Berisso, M. and Saccone, A. (2012) Searching for a Quantum Critical Point in Rh doped ferromagnetic Ce2.15Pd1.95In0.9. Journal of Physics: Conference Series, 391, Article ID: 012062. http://dx.doi.org/10.1088/1742-6596/391/1/012062
- Movahed, H.B. (2007) Inequalities Relating Critical Exponents. http://www.chem.utoronto.ca/~hbayat/HanifBayat-Inequalities
- Aharony, A. and Ahlers, G. (1980) Universal Ratios among Corrections to Scaling Amplitudes and Effective Critical Exponents. Physical Review Letters, 44, 782-785. http://dx.doi.org/10.1103/PhysRevLett.44.782
- Udodov, V. (2014) Violating of the Classical Essam-Fisher and Rushbrooke Formulas for Quantum Phase Transitions. arXiv:1404.0585v1 [cond-mat.stat-mech]
- Stishov, S.M. (2004) Quantum Phase Transitions. Physics-Uspekhi, 174, 853-860. http://dx.doi.org/10.3367/UFNr.0174.200408b.0853




