ABSTRACT

A new structure for isolator is proposed in this work. The proposed structure consists of metamaterial-magnetoplasma semiconductors parallel plate structure. The utility of magnetoplasma semiconductors is promising in developing nonreciprocal components in the submillimeter-wave and millimeter-wave bands for satellite communications. Metamaterials (MTMs) is used to enhance the behavior of the isolator.

1. Introduction

Isolators are needed in advanced satellite communications application in submillimeter wave energy bands with wavelength ranges between 1000 - 100 μm (300 GHz - 3 THz). Isolators use the TM_o mode only, the effective refractive index of which is different for forward and backward propagation, if the magnetization is properly adjusted [1]. The design and fabrication of isolators in the millimetric and submillimetric regions using properties of magnetoplasmons in semiconductors have been reported [2]. Metamaterials (MTMs) known as lefthanded substances are substances with simultaneous negative permittivity and permeability. The permittivity and the permeability are the only parameters of the substance that appear in the dispersion equation; therefore, they are the basic characteristic magnitudes which control the propagation of electromagnetic waves in matter. Authors [3,4] used MTMs in fabrication of isolators in combination of ferrite martials, garnet. However, there is a draw back for garnet that it has narrow bands at frequencies above 40 GHz due to the maximum saturation magnetization. This motivated several authors to investigate analytically and experimentally surface wave behavior along single gyroelectric or isotropic semiconductor interface [5-8] for purpose of isolator application. In this work, authors studied the possibility of enhancing the isolator behavior by studying the surface wave at the interface between semiconductor and MTMs. Further, the authors studied the behavior of the isolator at the vicinity of extraordinary wave resonance (EWR) which is an electromagnetic wave, partly transverse and partly longitudinal, which propagates perpendicular to applied magnetic field B. Next section introduces the basic theory of the proposed model. Numerical analysis is introduced in Section 3. The conclusion is given in Section 4.

2. Basic Theory

2.1. The Model

The geometry of the proposed configuration is displayed schematically in Figure 1. The direction of an external magnetic field is perpendicular to the direction of wave propagation in the waveguide. The structure comprises a semiconductor gallium arsenide (GaAs) substrate and a cover made of MTM.

The semiconductor is considered to be GaAs. The Drude-Zener model is applied to describe the interaction between the magnetically biased semiconductor and the field. In this work, the plasma or the ionic medium is characterized by the scalar permeability μ₀ and the fol-

lowing relative permittivity tensor [9]:

(1)

where

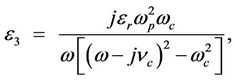
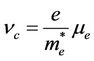, , ɛ_r is the relative permittivity, ω is the angular frequency, ω_p is the electron plasma frequency, ω_c is the cyclotron frequency, ν_c is the collision frequency, N_e is the density of nearly free electrons in the semiconductor, m_e^* is the effective electron mass, μ_e is the electron mobility and B is the applied magnetic flux density. In the Drude-Zener model the cyclotron frequency must be greater than the collision frequency. In the lossless case, ν_c = 0 the tensor entries reduces to

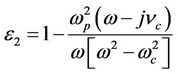(2)

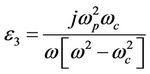(3)

Equations (2) and (3) show that there is a singularity at ω = ω_c. The Gyroelectric ratio, ε₃/ε₂, is defined as follows

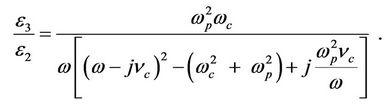(4)

Metamaterials (MTMs) has both negative permittivity ε_m and negative permeability µ_m. Both ε_m and µ_m are function of frequency as follows [10]

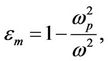(5)

(6)

In this work, we consider both ε_m and µ_m linear and lossless. The values of the parameters ω_r, ω_p, and F are chosen such that ε_m < 0 and µ_m <0.

2.2. Fields and Field Equations

In this study we only considered transverse magnetic fields (TM). The TM fields are assumed to have the following forms:

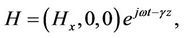(7)

where γ = α + jβ is the complex propagation constant. Applying Equations (7) and (8) into Maxwell’s equations we get the field equation for each medium. We can get the dispersion Equation (9) by applying the boundary conditions at y = 0, i.e. E_z and H_x must be continuous.

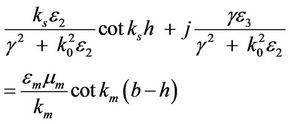(8)

where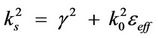, k₀ is the wave number is free space, 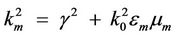, b is the total thickness of the waveguide, h is the thickness of the semiconductor layer as indicated in Figure 1, and

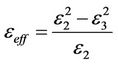(9)

In Equation (9), squaring γ gives linear term of the propagation constant β and second order term of β. The linear term of β made it possible to have an isolator from the proposed configuration.

3. Numerical Analysis

Equation (5) is numerically plotted in Figure 2 which

shows the permittivity ε_m of MTMs as function of frequency (ω). We notice that ε_m is negative for ω < ω_p = 150 π = 471.2 GHz. The permeability µ_m of MTMs, Equation (6) is plotted as function of frequency (ω) in Figure 3, we notice that µ_m is negative for

The real and imaginary parts of the effective permittivity as function of frequency are shown in Figure 4. In

the calculation we choose the value of collision frequency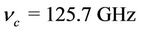, the value of cyclotron frequency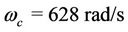. The values are chosen such that the Drude-Zener condition is satisfied. That is ω_c > ν_c. Figure 4 shows the extraordinary wave resonance (EWR) occurs at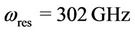. This is the region of our interest.

The dispersion Equation (9) is solved numerically. The forward and backward wave propagation is plotted as function of frequency as exhibited in Figure 5. In the calculation, b = 80 µm and h = 1/8 b.

It can be seen from Figure 5 that in the vicinity of the EWR the forward and backward propagation exhibits nonreciprocal effect. The maximum difference between both directions of propagation (forward and backward) occurs at frequency ω = 257 GHz.

4. Conclusion

We proposed a two layer system for an isolator. The proposed structure consists of semiconductor substrate and MTMs cover. The proposed structure exhibits a nonreciprocal device at the vicinity of EWR. The maximum phase difference occurs at 257 GHz.

REFERENCES