World Journal of Condensed Matter Physics
Vol.1 No.4(2011), Article ID:8762,9 pages DOI:10.4236/wjcmp.2011.14018
Thermal Properties of Ferrimagnetic Systems
![]()
Department of Physics, Alith Collage for Girls, Umm Alqura University, Mecca, KSA.
Email: aaomari@uqu.edu.sa, aiman101@hotmail.com
Received April 9th, 2011; revised April 21st, 2011; accepted May 10th, 2011.
Keywords: Ferrimagnet, alternat spins, susceptibility, heat capacity
ABSTRACT
The heat capacity of some ferrimagnets has additional structures like a shoulder in the Schottky-like peak, or emergence of a second peak when an external magnetic field is applied. It is shown here that the ferromagnetic and antiferromagnetic elementary excitation spectra give rise to two independent heat capacity peaks, one enveloped by the other, which add up to give the peak for the total system. Taking this into account helps understand the additional structures in the peaks. Moreover, the classification of ferrimagnets into predominantly antiferromagnetic, ferromagnetic, or a mixture of the two is shown to be validated by studying them under additional influences like dimerization and frustration. Because these two are shown to influence the ferromagnetic and antiferromagnetic dispersion relations—and hence the quantities like heat capacity and magnetic susceptibility—by different amounts, the characterization of ferrimagnetic systems (1,1/2), (3/2,1) and (3/2,1/2) is brought out more clearly. Both these influences enhance antiferromagnetic character. PACS numbers: 75.10.Jm, 75.50.Ge.
1. Introduction
Thermal properties of ferrimagnetic chains were theoretically investigated recently employing various methods like the modified spin-wave theory (MSWT) [1-4], density matrix renormalization group (DMRG) [2,3], quantum Monte Carlo method (QMC) [1,2,5], and Schwinger boson mead field theory (SB) [6]. The specific heat 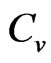 and magnetic susceptibility
and magnetic susceptibility 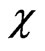 were shown to depend upon temperature as
were shown to depend upon temperature as 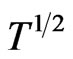 and
and 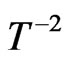 respectively at low temperatures, and
respectively at low temperatures, and 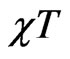 and
and  were shown to have, respectively, a rounded minimum [2,6-8] and a Schottkylike peak [2-5,7,8] at intermediate temperatures. The spin correlation length was shown to have a
were shown to have, respectively, a rounded minimum [2,6-8] and a Schottkylike peak [2-5,7,8] at intermediate temperatures. The spin correlation length was shown to have a 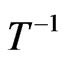 dependence at low temperature [1,9]. The modified spin wave theory, modified either by including Takahashi constraint or by including higher order corrections in the spin wave theory, was also shown to give results in surprisingly good agreement with those from quantum Monte Carlo method in the thermodynamic limit for this system [1,2].
dependence at low temperature [1,9]. The modified spin wave theory, modified either by including Takahashi constraint or by including higher order corrections in the spin wave theory, was also shown to give results in surprisingly good agreement with those from quantum Monte Carlo method in the thermodynamic limit for this system [1,2].
Ferrimagnetic systems have been classified into three categories: one with a predominantly Ferromagnetic (F) character, the second with a predominantly antiferromagnetic (AF) character, and the third with a mixture of the two. If the two spins constituting a ferrimagnet are 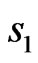 and
and  with
with , then it is conjectured [9,10] that the systems in the first category are those with
, then it is conjectured [9,10] that the systems in the first category are those with , those in the second category have
, those in the second category have , and the systems in the third category have
, and the systems in the third category have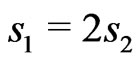 . We call it Yamamoto classification. Thus the system (
. We call it Yamamoto classification. Thus the system (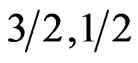 ) is ferromagnetic in character, (
) is ferromagnetic in character, (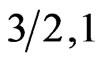 ) is antiferromagnetic, and (
) is antiferromagnetic, and (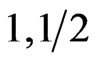 ) has a mixture of the two characters.
) has a mixture of the two characters.
The  vs temperature curves of different ferrimagnetic systems look alike—a rapidly decaying ferromagnetic part at low T, a rounded minimum at intermediate T and a linearly increasing antiferromagnetic part at high T—except that some systems like the predominately ferromagnetic (
vs temperature curves of different ferrimagnetic systems look alike—a rapidly decaying ferromagnetic part at low T, a rounded minimum at intermediate T and a linearly increasing antiferromagnetic part at high T—except that some systems like the predominately ferromagnetic (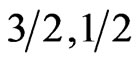 ) have a smaller rate of increase with temperature after the minimum compared to others. The heat capacities of the three systems also have quailtatively the same shape: a
) have a smaller rate of increase with temperature after the minimum compared to others. The heat capacities of the three systems also have quailtatively the same shape: a  dependence at low T, a Schottky-like peak and a decay at large temperatures. The MSW results on (
dependence at low T, a Schottky-like peak and a decay at large temperatures. The MSW results on (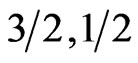 ) system, however, show a shoulder in the heat capacity below the peak temperature, which has been explained as being a result of the deficiency of the theory [11,12]. When an external magnetic field is applied, a second peak appears at low temperatures [13]. It is, therefore, quite likely that the heat capacity of ferrimagnets has, under suitable conditions, inherent structures like shoulders and double peaks. We would like in this paper to create such conditions and understand the nature of the heat capacity peak of ferrimagnets.
) system, however, show a shoulder in the heat capacity below the peak temperature, which has been explained as being a result of the deficiency of the theory [11,12]. When an external magnetic field is applied, a second peak appears at low temperatures [13]. It is, therefore, quite likely that the heat capacity of ferrimagnets has, under suitable conditions, inherent structures like shoulders and double peaks. We would like in this paper to create such conditions and understand the nature of the heat capacity peak of ferrimagnets.
In a recent work [14], we used a zero-temperature linear spin wave theory to study ferrimagnetic systems under the effects of dimerization and frustration, represented by the parameters  and
and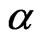 . Dimerization as well as the frustration were shown to affect the dispersion curves by either pushing them up or pulling them down in energy. Since this would change the gap that determines the heat capacity peak, these two effects are expected to influence the peak structure. It is also possible that they may give rise to additional peaks in heat capacity.
. Dimerization as well as the frustration were shown to affect the dispersion curves by either pushing them up or pulling them down in energy. Since this would change the gap that determines the heat capacity peak, these two effects are expected to influence the peak structure. It is also possible that they may give rise to additional peaks in heat capacity.
There were two distinct values of the frustration parameter; the transition point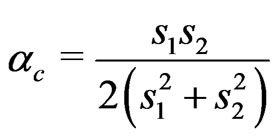 , that heralds transition from a commensurate ferrimagnetic state to a spiral state and the disorder value
, that heralds transition from a commensurate ferrimagnetic state to a spiral state and the disorder value  at which the energies become imaginary. The heat capacity and susceptibility are also expected to show the telltale signs of the transition induced by
at which the energies become imaginary. The heat capacity and susceptibility are also expected to show the telltale signs of the transition induced by .
.
Linear spin wave theory is known to give a fair picture in the case of ferromagnetic chains and gives only a qualitative picture for antiferromagnetic chains [11,12]. It has also been shown that it gives sufficiently good results for a ferrimagnetic system [15-18]. In a frustrated system, it has already been argued that the LSW theory yields satisfactory results at least in the limit of small frustration [17]. The use of LSW for larger values of frustration is indeed unreliable, but it is expected to give a qualitative picture that we are seeking here. As noted above, there was no remarkable improvement in the results at non-zero temperatures when linear spin wave theory was modified either by introducing a Takahashi constraint [11,12] or by including higher order corrections in the spin wave theory [1,2]. Nor were the results at zero temperature any more improved by considering non-linear spin wave theory [19]. The LSW theory is therefore expected to be valid in obtaining qualitative results even in the presence of dimerization and frustration in the thermodynamic limit.
In this paper we will study alternating spin systems formed with spin values (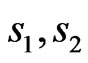 ) using linear spin wave theory. We investigate the temperature dependence of specific heat and susceptibility. We would like to see how the predominantly ferromagnetic, antiferromagnetic or mixed characters of the systems are brought out by subjecting them to dimerization and frustration. In particular, we would like to see the effect of the frustration-induced ferrimagnetic-to-spiral state phase transition on heat capacity and magnetic susceptibility. It is suggested that such peculiar effects will help identify the presence or absence of spin-Peierls dimerization and frustration in real low-dimensional ferrimagnetic systems.
) using linear spin wave theory. We investigate the temperature dependence of specific heat and susceptibility. We would like to see how the predominantly ferromagnetic, antiferromagnetic or mixed characters of the systems are brought out by subjecting them to dimerization and frustration. In particular, we would like to see the effect of the frustration-induced ferrimagnetic-to-spiral state phase transition on heat capacity and magnetic susceptibility. It is suggested that such peculiar effects will help identify the presence or absence of spin-Peierls dimerization and frustration in real low-dimensional ferrimagnetic systems.
2. Linear Spin Wave Theory
We consider a chain with spins 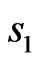 and
and 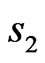 (
(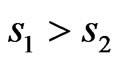 ) sitting on alternating sites with the possibility of lattice distortion leading to dimerization, and of competing antiferromagnetic nearest and next nearest neighbor couplings,
) sitting on alternating sites with the possibility of lattice distortion leading to dimerization, and of competing antiferromagnetic nearest and next nearest neighbor couplings, 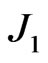 and
and 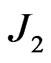 respectively. A two sublattice model of this system may be described by the Hamiltonian
respectively. A two sublattice model of this system may be described by the Hamiltonian
 (1)
(1)
with  belonging to one sublattice containing spins
belonging to one sublattice containing spins 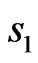 and
and  to the second sublattice containing spins
to the second sublattice containing spins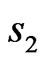 . The interaction
. The interaction 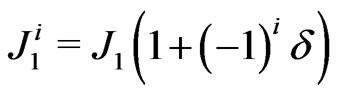 describes the alternate weaker and stronger couplings between two adjacent sites that may come about because of a spinPeierls dimerization of the lattice.
describes the alternate weaker and stronger couplings between two adjacent sites that may come about because of a spinPeierls dimerization of the lattice. 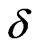 is the dimerization parameter. The degree of frustration is given by the ratio
is the dimerization parameter. The degree of frustration is given by the ratio
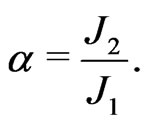
In the standard linear, non-interacting spin wave analysis, the above Hamiltonian is written in terms of bosonic spin-deviation operators with the help of HolsteinPrimakoff transformations, linearized and then diagonalized in terms of normal mode operators to
 (2)
(2)
The ground-state energy per unit cell  and the energies of the two excitation modes
and the energies of the two excitation modes  and
and  are given by
are given by
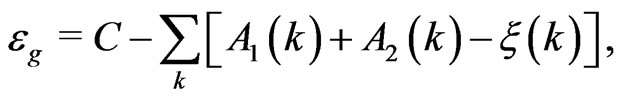 (3)
(3)
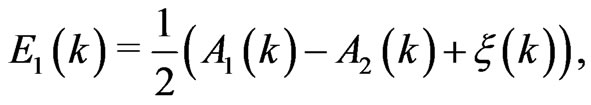 (4)
(4)
 (5)
(5)
In these equations
 (6)
(6)
 (7)
(7)
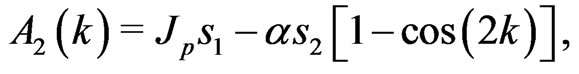 (8)
(8)
 (9)
(9)
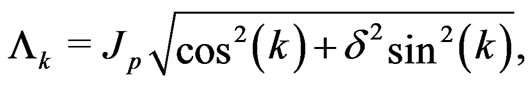 (10)
(10)
 (11)
(11)
where ,
, 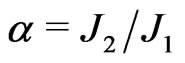 is the frustration parameter and
is the frustration parameter and 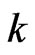 runs from
runs from 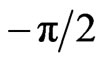 to
to  which is the first reduced Brillouin zone.
which is the first reduced Brillouin zone.
The free energy of the system is
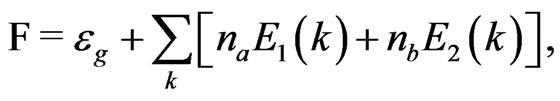 (12)
(12)
where  and
and 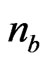 are the bose distribution functions for the two modes. It was reported earlier that the free energy decreases with increasing temperature [6] in a ferrimagnetic chain.
are the bose distribution functions for the two modes. It was reported earlier that the free energy decreases with increasing temperature [6] in a ferrimagnetic chain.
The static susceptibility 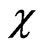 is
is
 (13)
(13)
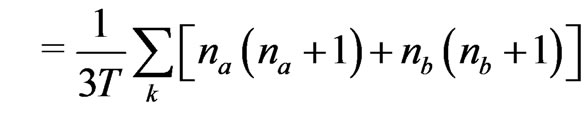 (14)
(14)
where . The product
. The product 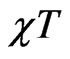 shows a minimum at intermediate temperatures, indicating that both the ferromagnetic and antiferromagnetic modes coexist in ferrimagnets.
shows a minimum at intermediate temperatures, indicating that both the ferromagnetic and antiferromagnetic modes coexist in ferrimagnets.
Specific heat  has a Schottky-like peak. In a textbook two level system, the peak is a result of the gap, and an increase in this gap makes the peak shift to higher values of temperature, and a decrease makes it shift to lower values.
has a Schottky-like peak. In a textbook two level system, the peak is a result of the gap, and an increase in this gap makes the peak shift to higher values of temperature, and a decrease makes it shift to lower values.
A ferrimagnet has two low lying excitations, one ferromagnetic in character (the acoustic dispersion) and the other antiferromagnetic (the optic dispersion curve). The Schottky like peak in the heat capacity is understood to be due to the two dispersion curves. In principle, because of the two excitation dispersion curves, one would expect this to behave like a three level system. But the heat capacity of a ferrimagnet does not follow the pattern of a 3 level system. Instead, from the non-interacting spin wave theory results of ferrimagnets, the contributions of the ferromagnetic and antiferromagnetic dispersions to the heat capacity of a ferrimagnet seem to be additive. The heat capacities calculated for the modes separately has each a Schottky-like peak structure, and the two add up to give the heat capacity of the ferrimagnet. This is also expected from the fact that in the absence of spin wave-spin wave interactions, the free energy is a sum of the ferromagnetic (F) and antiferromagnetic (AF) normal mode energies, as in Equation (12). The F and AF heat capacity peaks, which have the usual  and
and  dependence, respectively, at low temperatures, are mostly overlapping due to which the resultant heat capacity has a single peak. The additive nature of the two contributions is also reflected in the dependence of susceptibility on temperature. With increasing temperature, the ferromagnetic contribution decays earlier, while the antiferromagnetic one increases and persists up to higher temperatures [1,2,4,6-8,20,21].
dependence, respectively, at low temperatures, are mostly overlapping due to which the resultant heat capacity has a single peak. The additive nature of the two contributions is also reflected in the dependence of susceptibility on temperature. With increasing temperature, the ferromagnetic contribution decays earlier, while the antiferromagnetic one increases and persists up to higher temperatures [1,2,4,6-8,20,21].
The behavior of these physical quantities with temperature in the presence of dimerization  and frustration
and frustration 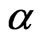 parameters for different system (
parameters for different system (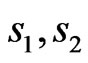 ); (
); (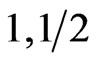 ), and (
), and (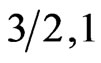 ), shall be discussed below. The effect of dimerization alone is discussed in section III, and that of frustrating alone in section IV.
), shall be discussed below. The effect of dimerization alone is discussed in section III, and that of frustrating alone in section IV.
3. Dimerized Chains
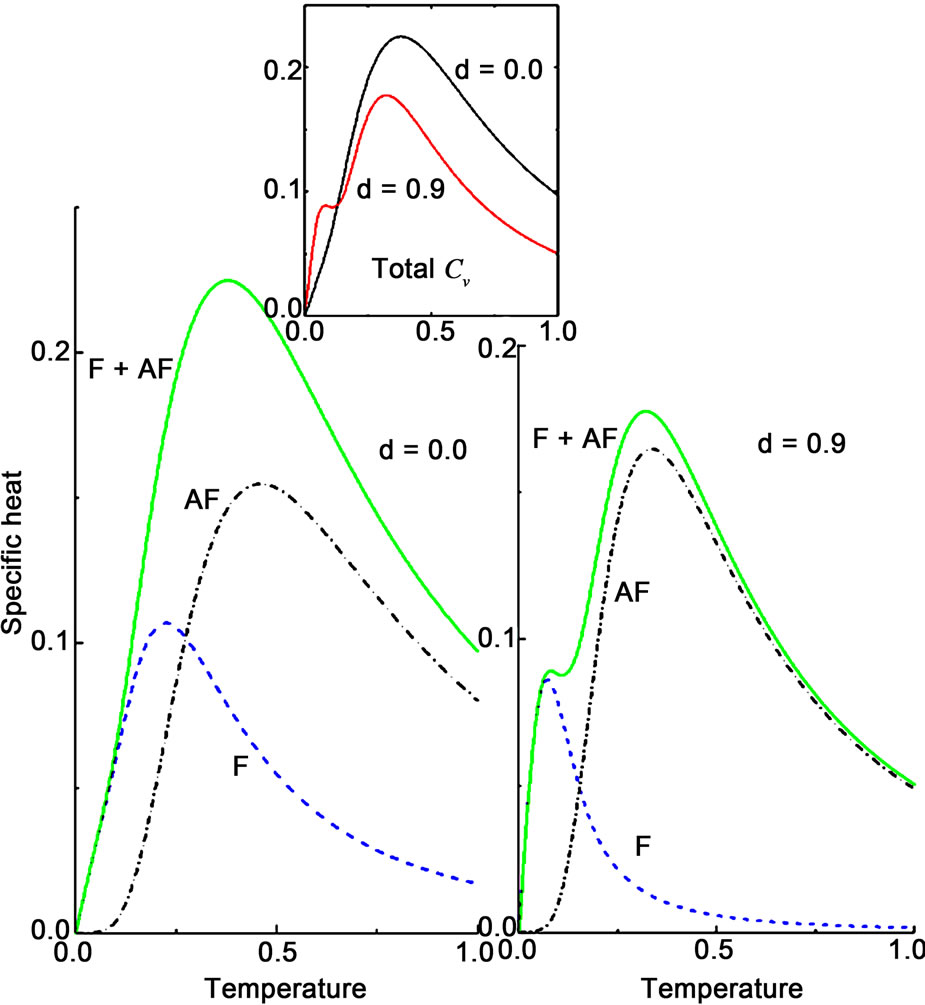
The effect of dimerization on the heat capacity of the (1,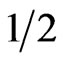 ) ferrimagnetic chain which is supposed to have a mixed F and AF characters is shown in Figure 1. Figure 1(a) gives the heat capacity without dimerization, and Figure 1(b) with
) ferrimagnetic chain which is supposed to have a mixed F and AF characters is shown in Figure 1. Figure 1(a) gives the heat capacity without dimerization, and Figure 1(b) with 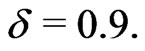 The figures show the heat capacities when the contributions of the ferromagnetic and antiferromagnetic excitation branches are taken separately and also when taken together. As expected, the total heat capacity is the sum of the heat capacities from the individual excitation branches in each case. It comes out that while both the F and AF peaks shift to lower temperatures with dimerization, the effect is different on
The figures show the heat capacities when the contributions of the ferromagnetic and antiferromagnetic excitation branches are taken separately and also when taken together. As expected, the total heat capacity is the sum of the heat capacities from the individual excitation branches in each case. It comes out that while both the F and AF peaks shift to lower temperatures with dimerization, the effect is different on
 (a) (b)
(a) (b)
Figure 1. Heat capacity for the chain (1,1/2) as a function of T. The heat capacities calculated with only the ferromagnetic (acoustic) branch of the elementary excitation spectrum and with only the antiferromagnetic (optic) branch are shown separately. Their sum is also shown which is exactly the heat capacity when the two excitation branches are taken into account together. Figure (a) is for δ = 0.0, and (b) for δ = 0.9. The inset for total Cv for the two values of δ highlights how the Schottky-like peak shifts in temperature, reduces in size, and acquires a shoulder. The curves are shown for the system (1, 1/2).
the two. The F peak shifts by a larger amount than the AF peak, and the magnitude of the AF peak increases with  while that of the F peak decreases. This is true for the other two ferrimagnetic systems (
while that of the F peak decreases. This is true for the other two ferrimagnetic systems ( ) and (
) and ( ) also, and appears to be a universal feature of a ferrimagnet, be it predominantly F, AF or a mixture the two characters. The increase and decrease in the AF and F peak magnitudes clearly shows that dimerization increases the antiferromagnetic character and decreases the ferromagnetic one. The net effect of this different effect is the emergence of the second peak in the total heat capacity, and a decrease in the magnitude of the main peak for the (1,
) also, and appears to be a universal feature of a ferrimagnet, be it predominantly F, AF or a mixture the two characters. The increase and decrease in the AF and F peak magnitudes clearly shows that dimerization increases the antiferromagnetic character and decreases the ferromagnetic one. The net effect of this different effect is the emergence of the second peak in the total heat capacity, and a decrease in the magnitude of the main peak for the (1,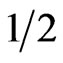 ) system, as shown in the inset. The predominantly F system (
) system, as shown in the inset. The predominantly F system (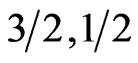 ) has this effect so accentuated that the shoulder, which in the LSW and MSW analyses is present even at
) has this effect so accentuated that the shoulder, which in the LSW and MSW analyses is present even at , turns into a double peak, as shown in Figure 2(a). The predominantly AF system (
, turns into a double peak, as shown in Figure 2(a). The predominantly AF system ( ), on the other hand, shows no second peak or even a shoulder, as in Figure 2(b). It is interesting to note that the difference arises despite the fact that the F and AF dispersion curves are lowered by an equal amount by dimerization. It appears to be a result of a more involved interplay of the
), on the other hand, shows no second peak or even a shoulder, as in Figure 2(b). It is interesting to note that the difference arises despite the fact that the F and AF dispersion curves are lowered by an equal amount by dimerization. It appears to be a result of a more involved interplay of the  -dependence of the excitation energies and the bosonic numbers in the free energy.
-dependence of the excitation energies and the bosonic numbers in the free energy.
The shift of the peaks to lower temperatures can be understood in terms of the energies of excitation. The heat capacity peaks are indeed Schottky-like peaks in that they are a result of the gaps in excitation spectra. The Schottky peak in the heat capacity of a simple textbook two-level system with a gap 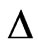 between the two levels has a position that shifts with the magnitude of
between the two levels has a position that shifts with the magnitude of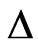 . As
. As 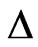 decreases, it shifts to lower temperatures, and vice versa. For a ferrimagnetic chain, contribution to the peak comes from all the modes which have well-defined dispersions in k-space, each mode having a different gap. With dimerization, the dispersion curves are lowered in energy, giving rise to a shift of the peak to lower temperatures.
decreases, it shifts to lower temperatures, and vice versa. For a ferrimagnetic chain, contribution to the peak comes from all the modes which have well-defined dispersions in k-space, each mode having a different gap. With dimerization, the dispersion curves are lowered in energy, giving rise to a shift of the peak to lower temperatures.
 (a) (b)
(a) (b)
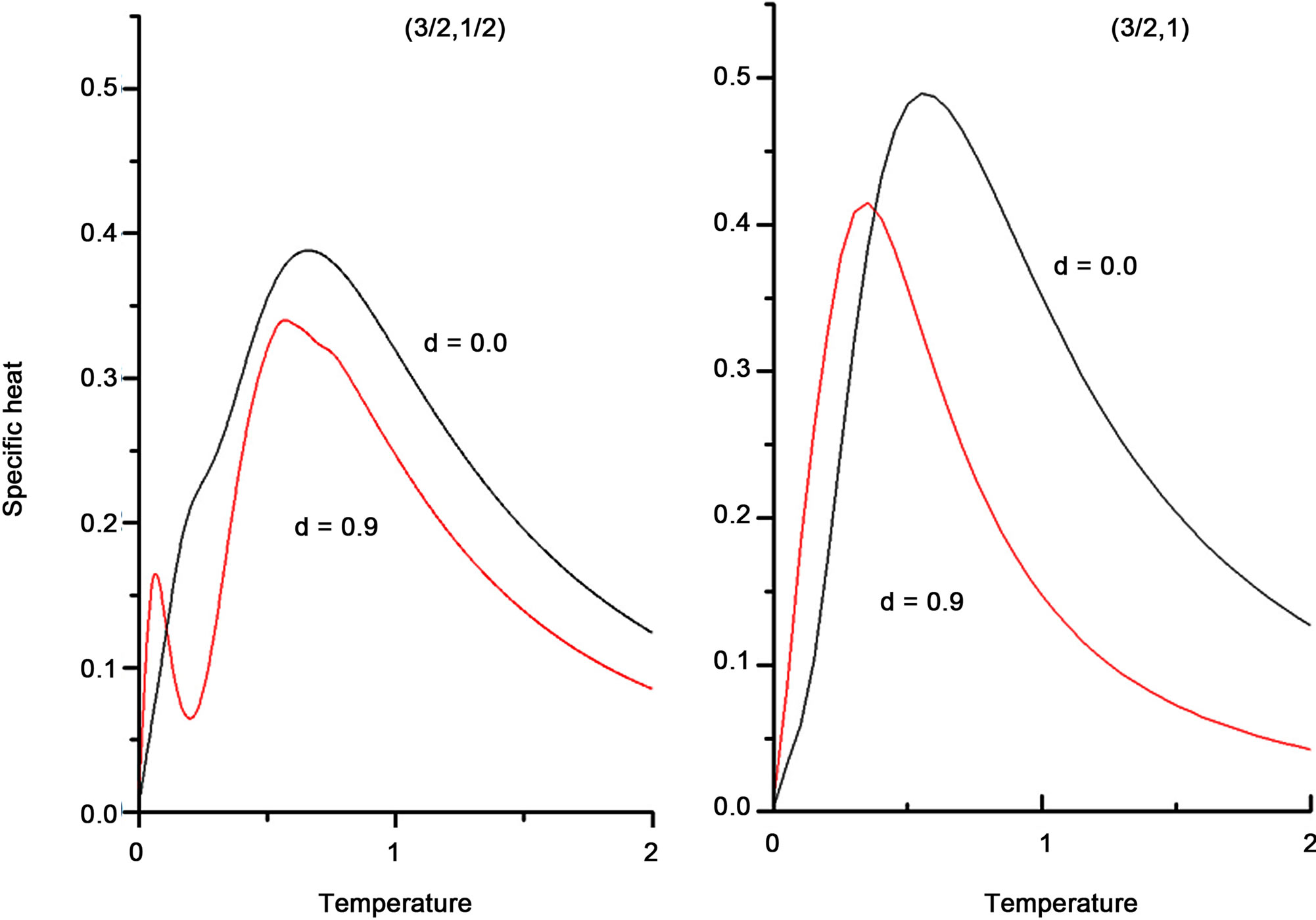
Figure 2. (a) Heat capacity of the ferrimagnetic chain (3/2, 1/2). This being a predominantly F system, the Schottky-like peak has a shoulder even in the absence of dimerization. The effect of dimerization is strong enough to separate out the F and AF peaks to result in a two-peak structure. (b) is for the predominantly AF system (3/2, 1) which fails to show a shoulder or a double peak structure even at large dimerization.
That the shifting is a result of the changes in the excitation spectra is also supported when the effect of dimerization on heat capacity is calculated by using a different parametrization of dimerization. We had earlier introduced 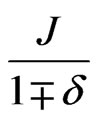 as another possibility [14,22]. The reasons are given in that reference. This parametrization has an opposite effect on the dispersion curves. Instead of decreasing in energy with
as another possibility [14,22]. The reasons are given in that reference. This parametrization has an opposite effect on the dispersion curves. Instead of decreasing in energy with  as in the case of the usual
as in the case of the usual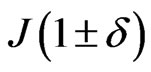 , the dispersion curves are now pushed up in energy with increasing
, the dispersion curves are now pushed up in energy with increasing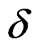 , with a nonlinear dependence on
, with a nonlinear dependence on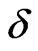 . Figure 3 shows the heat capacity of the (1,
. Figure 3 shows the heat capacity of the (1,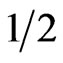 ) chain with this parametrization. The Schottky peaks now shift to higher temperatures with increasing
) chain with this parametrization. The Schottky peaks now shift to higher temperatures with increasing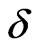 . Also, the individual F and AF peaks respond differently to
. Also, the individual F and AF peaks respond differently to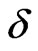 . Just as the rate of increase of the AF dispersion curve with
. Just as the rate of increase of the AF dispersion curve with 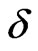 is much larger at higher
is much larger at higher 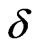 values than that of the F dispersions, the AF Schottky peak shifts by a much larger amount than the F peak. Consequently, there comes a time when the AF peak is pushed so far to the high temperature side that a double peak structure develops. This appears more clearly in the case of the (
values than that of the F dispersions, the AF Schottky peak shifts by a much larger amount than the F peak. Consequently, there comes a time when the AF peak is pushed so far to the high temperature side that a double peak structure develops. This appears more clearly in the case of the (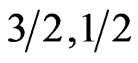 ) ferrimagnetic chain in which ferromagnetic character dominates. This is shown in Figure 4. The AF peak is so strongly pushed to higher temperatures that the F and AF peaks almost separate from each other. Correspondingly, in the dispersion curves of this system, the optic mode is pushed up by a far larger magnitude than the acoustic one. This establishes then that the heat capacity peaks reflect the effects an external or internal influence has on the dispersion curves.
) ferrimagnetic chain in which ferromagnetic character dominates. This is shown in Figure 4. The AF peak is so strongly pushed to higher temperatures that the F and AF peaks almost separate from each other. Correspondingly, in the dispersion curves of this system, the optic mode is pushed up by a far larger magnitude than the acoustic one. This establishes then that the heat capacity peaks reflect the effects an external or internal influence has on the dispersion curves.
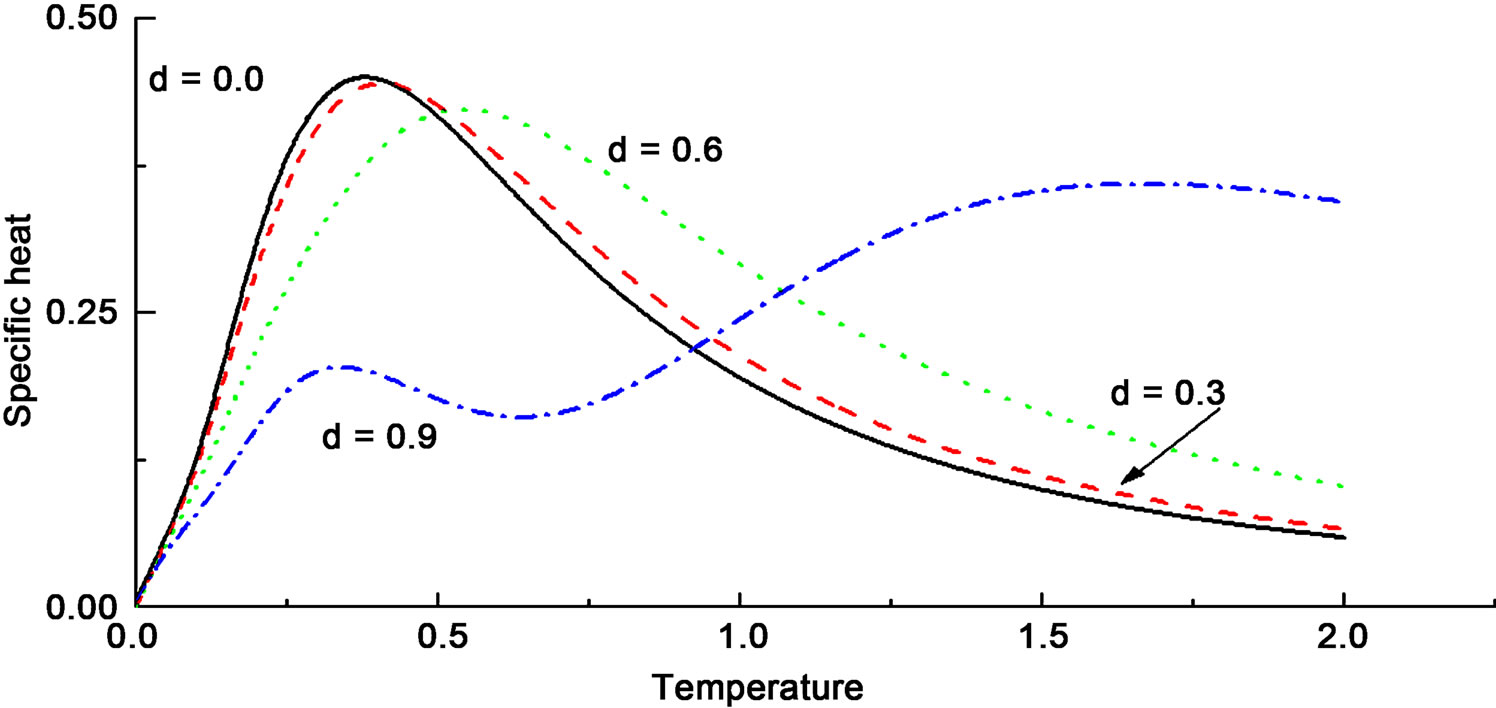
Figure 3. The dependence of heat capacity on T when the dimerization is parametrized by the interaction 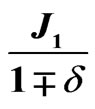 for the alternating spin chain (1, 1/2). The shift in the Schottky-like peak is to higher T, in contrast to the shift to lower T in Figure 1. A large dimerization pushes the AF peak much farther than the F peak, resulting in a two-peak structure.
for the alternating spin chain (1, 1/2). The shift in the Schottky-like peak is to higher T, in contrast to the shift to lower T in Figure 1. A large dimerization pushes the AF peak much farther than the F peak, resulting in a two-peak structure.

Figure 4. The heat capacity for the alternating spin chain (3/2, 1/2) with the parametrization as in Figure 3. The F and AF peaks are now very dramatically separated.
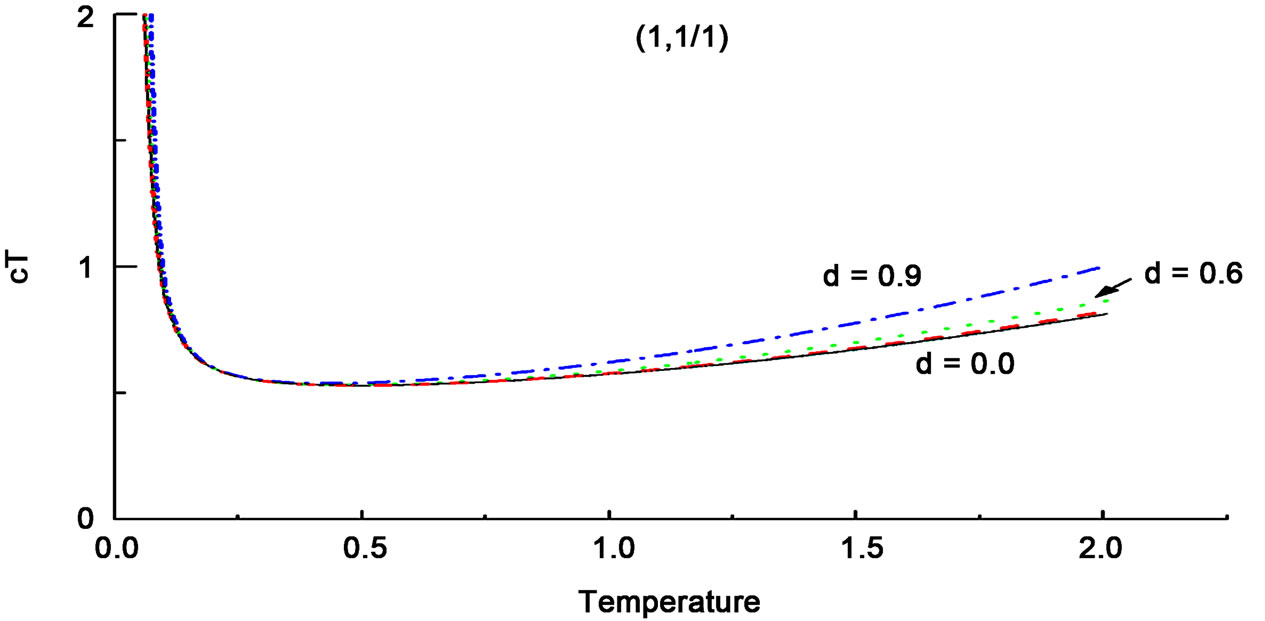
The change of character upon dimerization shows up in the susceptibility of ferrimagnets also. Figure 5 shows 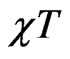 vs T, the low temperature part of which is dominated by the F contribution and the high temperature part by the AF contribution. The minimum at intermediate temperatures is a result of a comparable contributions of the two. With dimerization using
vs T, the low temperature part of which is dominated by the F contribution and the high temperature part by the AF contribution. The minimum at intermediate temperatures is a result of a comparable contributions of the two. With dimerization using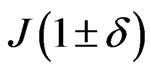 , the increase in the slope at high temperatures testifies to the increasing AF character of a ferrimagnet. This increase is the largest for the predominantly AF (
, the increase in the slope at high temperatures testifies to the increasing AF character of a ferrimagnet. This increase is the largest for the predominantly AF ( ) system; Figure 5(c), smaller for the (
) system; Figure 5(c), smaller for the (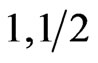 ) system; Figure 5(a) and the smallest for the predominantly ferromagnetic (
) system; Figure 5(a) and the smallest for the predominantly ferromagnetic (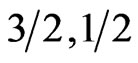 ) system; Figure 5(b), showing again the validity of the Yamamoto classification.
) system; Figure 5(b), showing again the validity of the Yamamoto classification.
 (a)
(a) (b)
(b)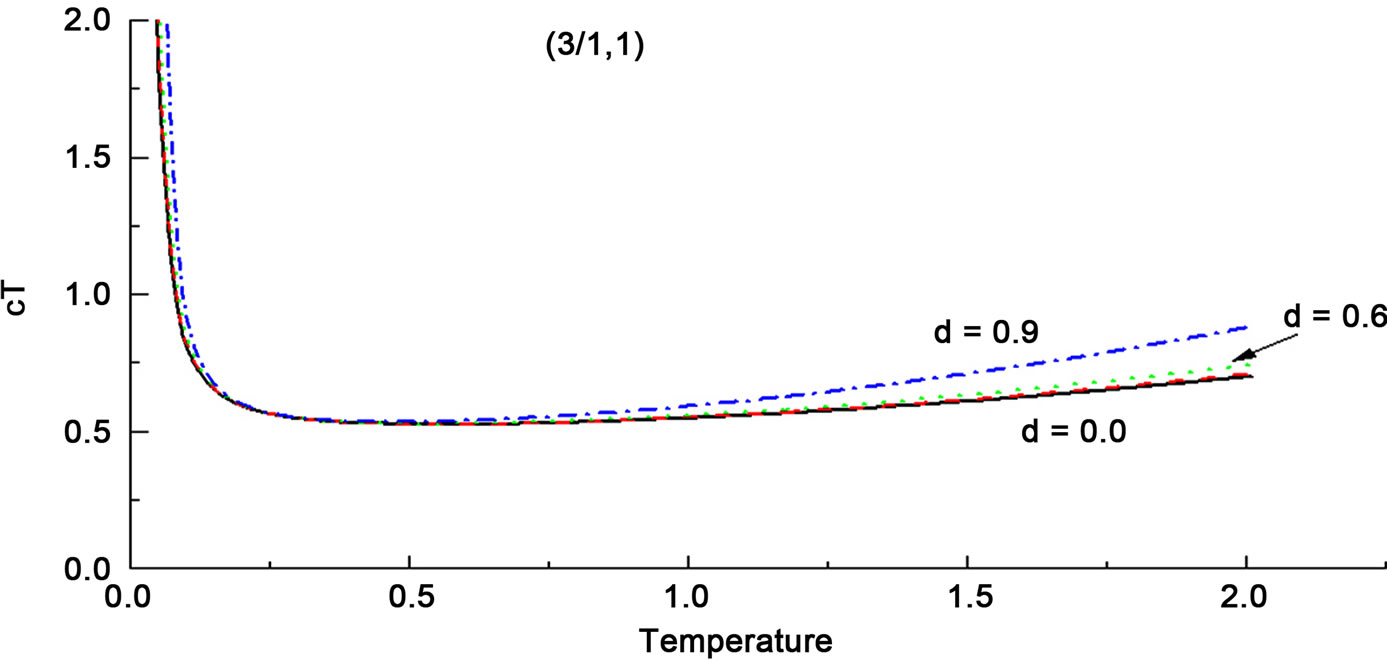 (c)
(c)
Figure 5. The χT vs T in ferrimagnetic chains: (a) for the system (1, 1/2), (b) for (3/2, 1/2) and (c) for (3/2, 1), for various values of the dimerization parameter δ. That dimerization enhances the AF character of ferrimagnets is clearly observable here.
4. Frustrated Ferrimagnetic Chains
The effect of frustration in ferrimagnetic systems has been investigated [4,14,17] at zero temperature. Two key values of the frustration parameter were identified; namely, 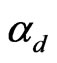 and
and . At any finite temperature, we find that within the linear spin wave theory the two are temperature independent. We will study the thermal effect of a frustrated chain in the absence of dimerization.
. At any finite temperature, we find that within the linear spin wave theory the two are temperature independent. We will study the thermal effect of a frustrated chain in the absence of dimerization.
The effect of frustration on heat capacity will again be discussed for the F and AF contributions separately. Frustration causes the AF  peak to slightly increase in size and shift to lower temperatures. But its effect on the
peak to slightly increase in size and shift to lower temperatures. But its effect on the  peak due to the F excitation modes is more dramatic. Here the transition to the spiral phase at
peak due to the F excitation modes is more dramatic. Here the transition to the spiral phase at 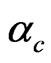 has its impact. Before
has its impact. Before  the peak decreases in size and shifts to lower temperatures. Beyond this value, when the system goes into the spiral phase, a further increase in frustration causes the peak to increase in size and shift to higher temperatures. All of this is a result of the modesoftening changes that the F dispersion curves go through, as seen in Figure 6. The total
the peak decreases in size and shifts to lower temperatures. Beyond this value, when the system goes into the spiral phase, a further increase in frustration causes the peak to increase in size and shift to higher temperatures. All of this is a result of the modesoftening changes that the F dispersion curves go through, as seen in Figure 6. The total 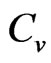 being a sum of the AF and F contributions in the non-interacting spin-wave theory changes with
being a sum of the AF and F contributions in the non-interacting spin-wave theory changes with 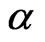 as shown in Figure 7.
as shown in Figure 7.
In the case of the (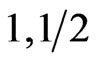 ) system, the
) system, the  chain having a mixed F and AF characters, the
chain having a mixed F and AF characters, the  curve has an AF-like
curve has an AF-like  dependence at low temperatures. With added frustration, the F peak separates out at low temperatures making the total
dependence at low temperatures. With added frustration, the F peak separates out at low temperatures making the total 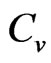 curve have an F-like
curve have an F-like  dependence at low T. The F peak diminishes in size with increasing
dependence at low T. The F peak diminishes in size with increasing , almost vanishing at
, almost vanishing at , beyond which it regrows and eventually merges with the AF peak. At this point the
, beyond which it regrows and eventually merges with the AF peak. At this point the  curve again has an AF-like
curve again has an AF-like  dependence at low temperatures. This is shown in Figure 7(a).
dependence at low temperatures. This is shown in Figure 7(a).
In the case of the predominantly F system (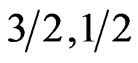 ), the heat capacity of which has a low temperature shoulder due to the F peak even in the absence of frustration, the changes affecting the F peak are very prominent, as in Figure 7(b). As
), the heat capacity of which has a low temperature shoulder due to the F peak even in the absence of frustration, the changes affecting the F peak are very prominent, as in Figure 7(b). As 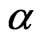 increases, the F peak separates out and diminish in size before
increases, the F peak separates out and diminish in size before , after which it rises and eventually merges with the AF peak. The net
, after which it rises and eventually merges with the AF peak. The net 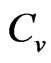 also experiences a low-temperature cross-over from a ferromagnetic
also experiences a low-temperature cross-over from a ferromagnetic 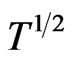 dependence at zero frustration to the antiferromagnetic
dependence at zero frustration to the antiferromagnetic  dependence at
dependence at 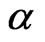 beyond
beyond 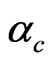 in the spiral state.
in the spiral state.
In the case of the predominantly AF system (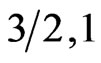 ), the F peak in itself experiences the same changes as in the (
), the F peak in itself experiences the same changes as in the (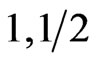 ) system, but it remains submerged in the AF peak, and the net
) system, but it remains submerged in the AF peak, and the net  never shows a second peak, as in Figure 7(c). It, however, also experiences the cross-over from
never shows a second peak, as in Figure 7(c). It, however, also experiences the cross-over from 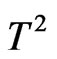 to
to 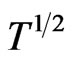 behavior at low temperatures.
behavior at low temperatures.

Figure 6. The dependence of the excitation energies on frustration parameter α for the spin system (1, 1/2) shows the mode softening that heralds the transition to spiral state.
 (a)
(a)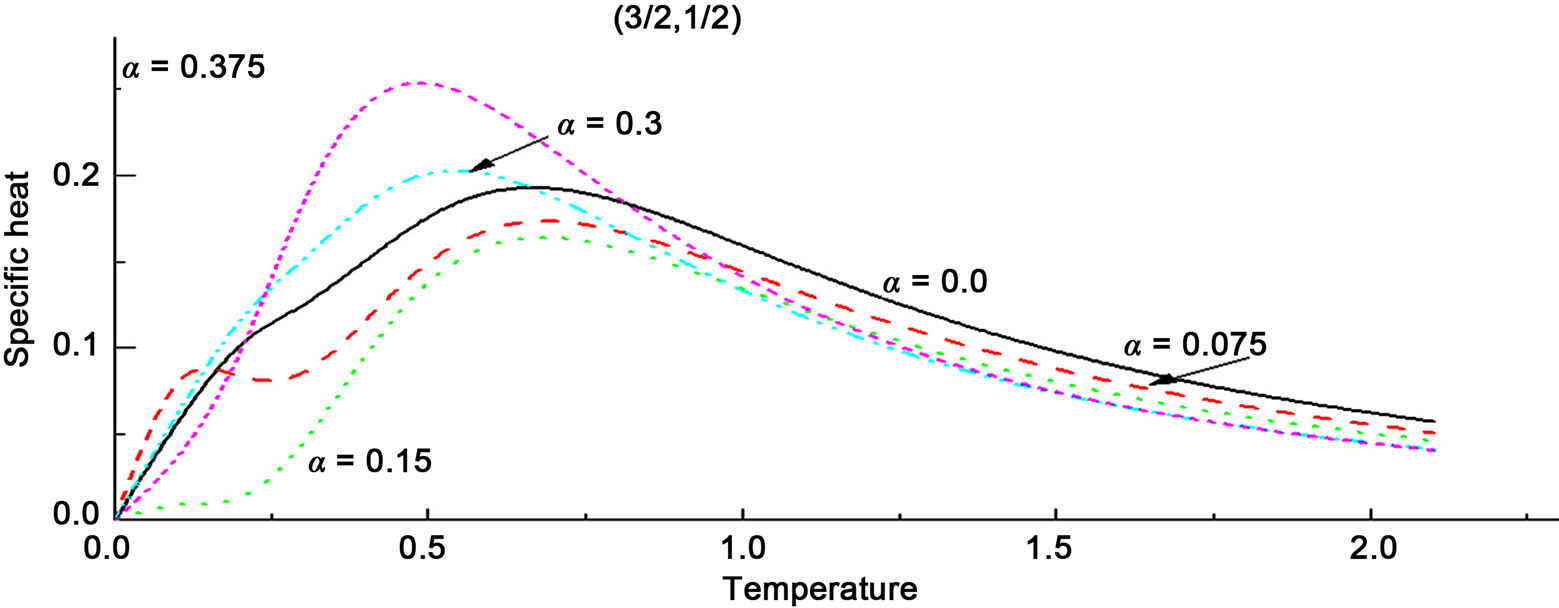 (b)
(b) (c)
(c)
Figure 7. Specific heat vs T: (a) for the spin system (1, 1/2), (b) for (3/2, 1/2) and (c) for (3/2, 1), for various values of the frustration parameter α.
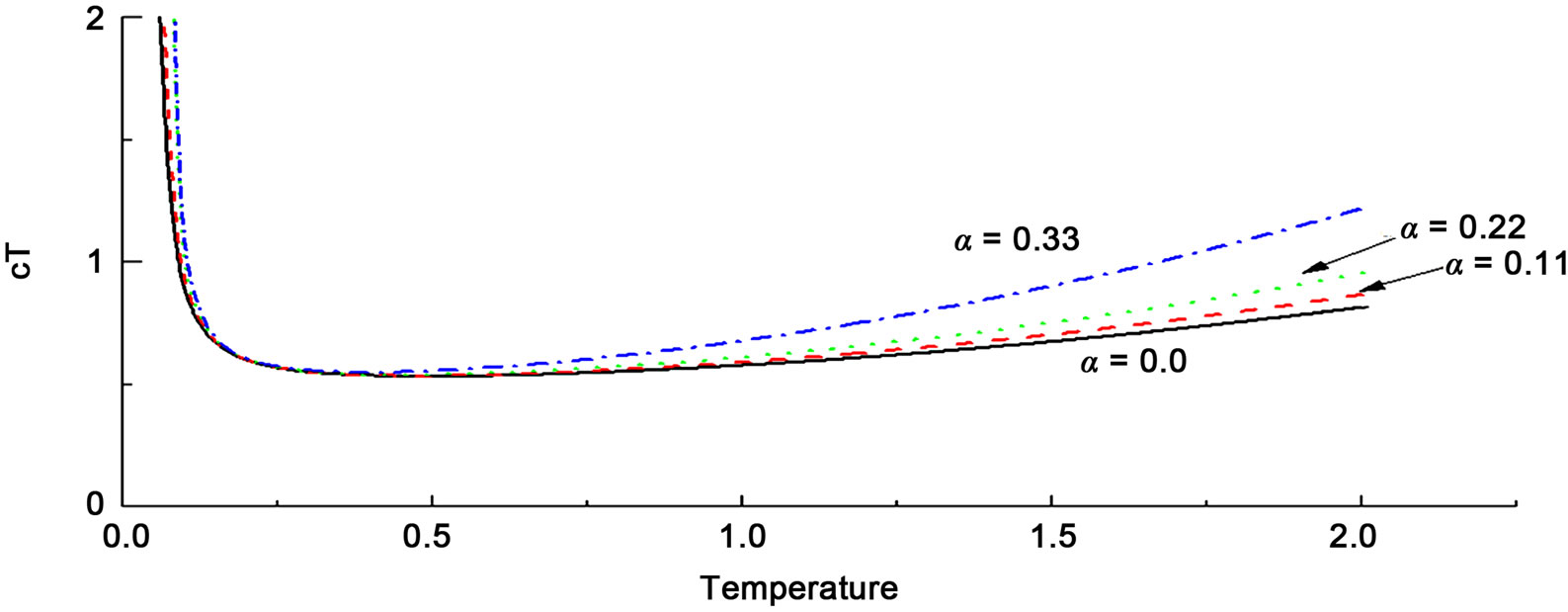
Figure 8. The behavior of χT vs T of the ferrimagnetic system (1, 1/2) on a chain for different values of α.
The effect of frustration on 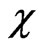 is the same as that of dimerization. The minimum shifts to lower temperatures and the slope of the high temperature tail increases as shown in Figure 8.
is the same as that of dimerization. The minimum shifts to lower temperatures and the slope of the high temperature tail increases as shown in Figure 8.
In short, the effect of dimerization and frustration on the thermal behavior provides a nice evidence of the validity of the Yamamoto classification of ferrimagnetic chains.
We thus conclude that the heat capacity of a ferrimagnet can have a more complicated structure than a simple Schottky-like peak. It can have a low temperature shoulder or a double peak structure. The peak can shift to lower or higher temperatures and can also change in size depending upon the influences the system is undergoing. All of this can be understood in terms of the component ferromagnetic and antiferromagnetic peaks that retain their individuality. The Yamamoto classification of the ferrimagnetic systems into predominantly ferromagnetic (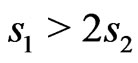 ), antiferromagnetic (
), antiferromagnetic (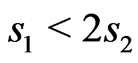 ) and ferrimagnetic (
) and ferrimagnetic (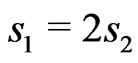 ) appears to have a basis in this characteristic.
) appears to have a basis in this characteristic.
The author would like to thank Wu Congjun for discussion and help.
REFERENCES
- S. Yamamoto and T. Fukui, “Thermodynamic Properties of Heisenberg Ferrimagnetic Spin Chains: Ferromagnetic-Antiferromagnetic Crossover,” Physical Review B, Vol. 57, No. 22, 1998, pp. 14008-14011. doi:10.1103/PhysRevB.57.R14008
- S. Yamamoto, T. Fukui, K. Maisinger and U. Schollowock, “Combination of Ferromagnetic and Antiferromagnetic Features in Heisenberg Ferrimagnets,” Journal of Physics: Condfensed Matter, Vol. 10, No. 48, 1998, p. 11033. doi:10.1088/0953-8984/10/48/023
- S.-S. Gong, W. Li, Y. Zhao and G. Su, “Magnetism and Thermodynamics of Spin-(1/2, 1) Decorated Heisenberg Chain with Spin-1 Pendants,” Physical Review B, Vol. 81, No. 21, 2010, pp. 214431-214439. doi:10.1103/PhysRevB.81.214431
- N. B. Ivanov, “Spin Models of Quasi-1D Quantum Ferrimagnets with Competing Interactions,” Condensed Matter Physics, Vol. 12, No. 3, 2009, pp. 435-447. doi:10.5488/CMP.12.3.435
- W Selke and J. Oitmaa, “Monte Carlo Study of MixedSpin S = (1/2, 1) Ising Ferrimagnets,” Journal of Physics: Condfensed Matter, Vol. 22, No. 7, 2010, p. 76004. doi:10.1088/0953-8984/22/7/076004
- C. Wu, B. Chen, X. Dai, Y. Yu and Z.-B. Su, “Schwinger-Boson Mean-Field Theory of the Heisenberg Ferrimagnetic Spin Chain,” Physical Review B, Vol. 60, No. 2, 1999, pp. 1057-1063. doi:10.1103/PhysRevB.60.1057
- S. K. Pati, S. Ramasesha and D. Sen, “Low-Lying Excited States and Low-Temperature Properties of an Alternating Spin-1-Spin-1/2 Chain: A Density-Matrix Renormalization-Group Study,” Physical Review B, Vol. 55, No. 14, 1997, pp. 8897-8904. doi:10.1103/PhysRevB.55.8894
- S. K. Pati, S. Ramasesha and D. Sen, “A Density Matrix Renormalization Group Study of Low-Energy Excitations and Low-Temperature Properties of Alternating Spin Systems,” Journal of Physics: Condfensed Matter, Vol. 9, No. 41, 1997, p. 8707.
- S. Yamamoto and T. Sakai, “Low-Energy Structure of Heisenberg Ferrimagnetic Spin Chains,” Journal of the Physical Society of Japan, Vol. 67, 1998, pp. 3711-3714. doi:10.1143/JPSJ.67.3711
- S. Yamamoto, “Magnetic Properties of Quantum Ferrimagnetic Spin Chains,” Physical Review B, Vol. 59, No. 2, 1999, pp. 1024-1027. doi:10.1103/PhysRevB.59.1024
- S. Yamamoto, T. Fukui and T. Sakai, “Characterization of Ferrimagnetic Heisenberg Chains According to the Constituent Spins,” cond-mat/0001004 (2000).
- S. Yamamoto, “Modified Spin-Wave Description of the Nuclear Spin Relaxation in Ferrimagnetic Heisenberg Chains,” cond-mat/ 0004297 (2000).
- K. Maisinger, U. Schollwöck, S. Brehmer, H.-J. Mikeska, and S. Yamamoto, “Thermodynamics of the (1, 1/2) Ferrimagnet in Finite Magnetic Fields,” Physical Review B, Vol. 58, No. 10, 1998, pp. 5908-5911. doi:10.1103/PhysRevB.58.R5908
- A. Al-Omari and A. H. Nayyar, “The Combined Effect of Frustration and Dimerization in Ferrimagnetic Chains and Square Lattices,” Journal of Physics: Condfensed Matter, Vol. 12, No. 48, 2000, p. 1194. doi:10.1088/0953-8984/12/48/311
- S. Brehmer, H. -J. Mikeska and S. Yamamoto, “Low-Temperature Properties of Quantum Antiferromagnetic Chains with Alternating Spins S = 1 and S = 1/2,” Journal of Physics: Condfensed Matter, Vol. 9, No. 19, 1997, p. 3921. doi:10.1088/0953-8984/9/19/012
- S. Yamamoto, S. Brehmer and H.-J. Mikeska, “Elementary Excitations of Heisenberg Ferrimagnetic Spin Chains,” Physical Review B, Vol. 57, No. 21, 1998, p. 13610.
- N. Ivanov, J. Richter and U. Schollwock, “Frustrated Quantum Heisenberg Ferrimagnetic Chains,” Physical Review B, Vol. 58, No. 21, 1998, pp. 14456-14461. doi:10.1103/PhysRevB.58.14456
- N. Ivanov, “Spin-Wave Series for Quantum One-Dimensional Ferrimagnets,” Physical Review B, Vol. 57, No. 22, 1998, p. 14024.
- A. Al-Omari, “Self-Consistent Approximation for Dimerization of Ferrimagnets on Chains and Square Lattices,” Physical Review B, Vol. 59, No. 14, 1999, pp. 9304-9313. doi:10.1103/PhysRevB.59.9304
- T. Sarkar, V. Pralong, V. Caignaert and B. Raveau, “Competition between Ferrimagnetism and Magnetic Frustration in Zinc Substituted YBaFe4O7,” Chemistry of Materials, Vol. 22, No. 9, 2010, p. 2885.
- A. Winkler, N. Narayanan, D. Mikhailova, K. G. Bramnik, H. Ehrenberg, H. Fuess, G. Vaitheeswaran, V. Kanchana, F. Wilhelm, A. Rogalev, A. Kolchinskaya and L. Alff, “Magnetism in Re-Based Ferrimagnetic Double Perovskites,” New Journal of Physics, Vol. 11, No. 7, 2009, p. 73047. doi:10.1088/1367-2630/11/7/073047
- A. Al-Omari and A. H. Nayyar, “Dimerization of Ferrimagnets on Chains and Square Lattices,” Journal of Physics: Condfensed Matter, Vol. 11, No. 2, 1999, p. 465. doi:10.1088/0953-8984/11/2/012

