Atmospheric and Climate Sciences
Vol.4 No.1(2014), Article ID:40945,6 pages DOI:10.4236/acs.2014.41001
Application of Clausius-Clappeyron Relation (1832) and Carnot Principle (1824) to Earth’s Atmosphere Tricellular Circulation
Laboratory of Earth’s Atmosphere Physics, Department of Physics, University of Yaoundé I, Yaoundé, Cameroun
Email: cesar.mbane@yahoo.fr
Copyright © 2014 Mbane Biouele César. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Mbane Biouele César. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 3, 2013; revised November 2, 2013; accepted November 10, 2013
Keywords:Combination of Elementary Events; Groundor Space-Based Observations; Earth’s Atmosphere Tricellular Circulation
ABSTRACT
Atmospheric or climate phenomena are usually a combination of elementary events whose scales range from the very small (microscopic) to the infinitely large (synoptic). This means that build reasoning from groundor space-based observations only, regardless of the physics of elementary processes, inevitably leads to erroneous results. Given the fact that plots of Troposphere Tricellular Circulation are only based on weather mean conditions measured near the ground (i.e.: pressure and winds fields observed at the surface of the earth), we want to improve these representations of the general circulation of the atmosphere, by using both Clausius-Clapeyron Relation and Carnot Principle derived respectively in 1832 and 1824. Indeed, Clausius-Clapeyron relation shows precisely that, unlike the dry water vapor that can be assimilated to the ideal gas at many circumstances, the saturated water vapor has, in an air parcel at the same time cold (temperature below 0.0098˚C) and rich in moisture (vapor pressure above 6.11 mb), thermoelastic properties diametrically opposed to those of ideal gas (including dry water vapor). Vertical profiles of temperature and water vapor in the atmosphere provided by groundor space-based observations lead to the location of a troposphere region in which the ideal gas assumption should be banned: hence appropriate and unique plot of earth’s atmosphere tricellular circulation.
1. Introduction
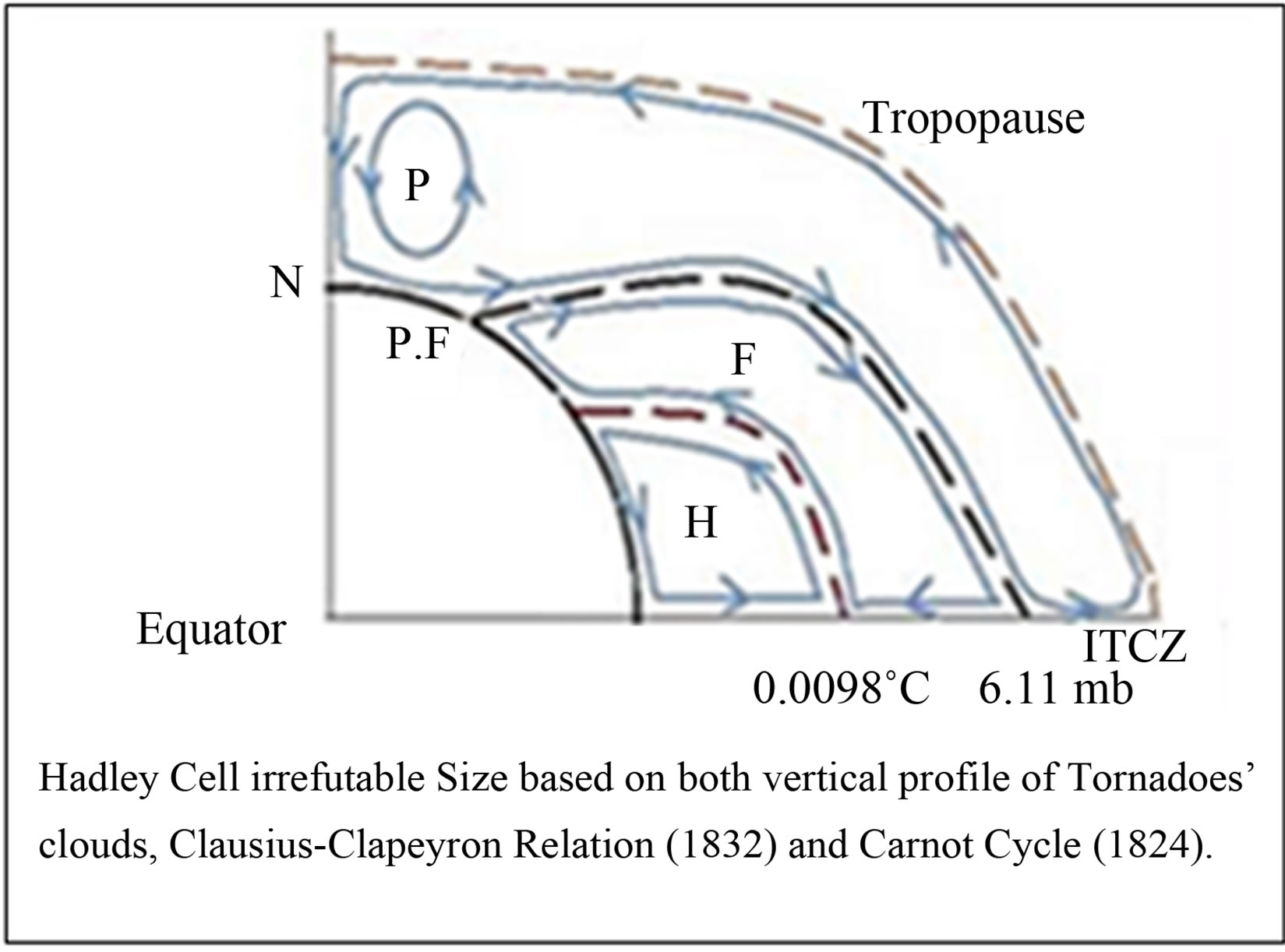
It is now proven that between the two equal level surfaces of temperature and water vapors rating respectively at 0.0098˚C and 6.11 mb, troposphere thermoelastic properties are diametrically opposed to those of the ideal gas [1-4]. The consequences of this revelation on our perception of climate phenomena are many. For instance, hot air is not always lighter than cold air throughout the troposphere. This thermodynamic property was unfortunately unknown to public and has led to numerous errors and inconsistencies that abound in many Atmospheric and Climate Sciences publications (including audiovisuals productions). Before using perfect gas assumption everyone must now remember that one of the constituents of the atmosphere (saturated water vapor in this case) has, depending on the location, behavior diametrically opposite to that of ideal gas. This subtle precaution allows avoiding misinterpretations like that updrafts are necessarily associated with warming or that downdrafts are necessarily associated with cooling [5-24]. ClausiusClapeyron formula combined with Carnot principle strengthens our knowledge of the passive convection movements (through-out the troposphere) and finally allows earth’s atmosphere tricellular circulation thermodynamics and kinematics. Each of us will now easily see that the presence of water substance in all three states in the earth’s atomsphere gives to troposphere the exclusivity of a general circulation consists of three groups of passive convective cells (Hadley, Ferrel, and Polar) on either side of the ITCZ (Inter Tropical Convergence Zone).
2. Clausius-Clapeyron (1832) Impacts on Troposphere Dynamic Balance
Atmosphere dynamics uses precise concept of air particle [25-27]. Especially:
1) Few exchanges on molecular scale: it is easy to follow quantity of air which preserves certain properties.
2) Quasi-static equilibrium: at any moment there is dynamic balance, i.e., the particle has the same pressure as its environment (P = Pext).
3) No thermal balance: heat transfers by conduction are very slow and neglected. One can have T ≠ Text.
4) The horizontal sizes of the air particle can go from a few cm to 100 km according to the applications.
Taking into account the fact that the atmosphere is mainly composed of dry air and water vapor, the Dalton’s law connects the pressure (P) with the partial pressure of dry air (Pa) and saturated water vapor (ew)
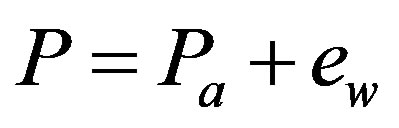 (1)
(1)
In deriving (P) with respect to the temperature, one has
 (2)
(2)
According to the Quasi-static equilibrium (or dynamic balance) the pressure of the parcel of air must be the same as that of the ambient air, including during sudden local changes in phases by water contained in this parcel. Reality that all meteorologists restore through the following famous sentence: the phases change takes place at constant pressure. Thereby write Equation (3),
 (3)
(3)
Equations (2) and (3) lead to the derivative of V compared to T
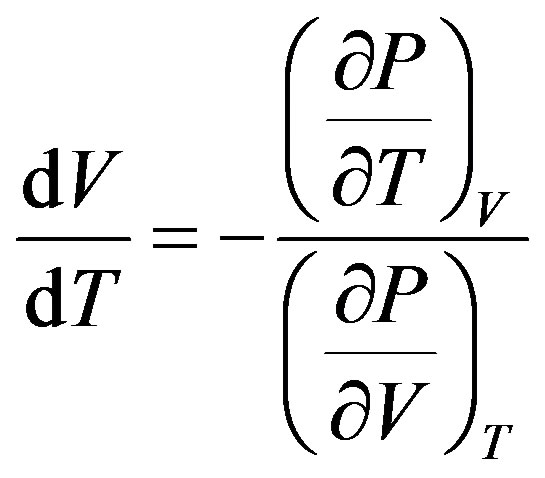 (4)
(4)
Introducing the coefficient of thermal expansion of moist air at constant temperature
 (5)
(5)
Then the fundamental relationship of atmosphere dynamic balance:
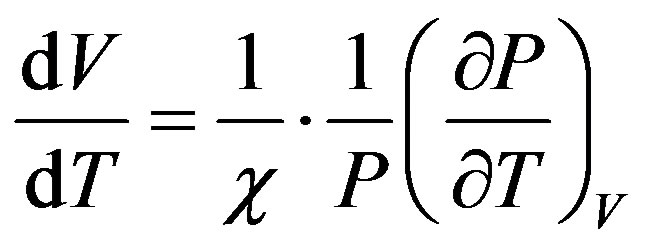 (6)
(6)
One can also write equation of atmosphere dynamic balance in terms of partial pressures
 (7)
(7)
Or,
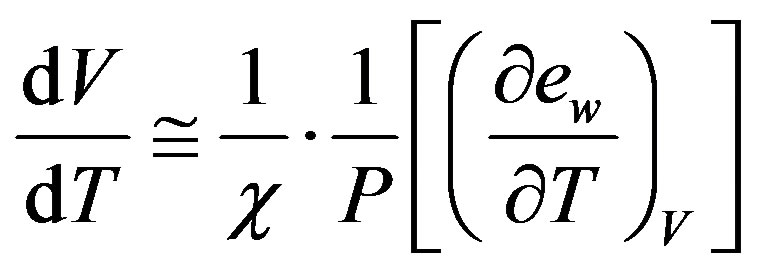 (8)
(8)
Relations (6) and (7) lead to a very important atmosphere dynamics statement:
At any moment and throughout the atmosphere, one can use Equations (6) or (7) and Clausius-Clapeyron slope of the equilibrium curves in the pT-plane (Figure 1) to predict in which direction the air parcel will move (up or down) if its temperature increases or decreases. Table 1 and Figure 2" target="_self"> Figure 2 provide an overview of possible situations in the troposphere.
3. Application of Carnot Principle (1832) to Mean Meridional Circulation
3.1. Carnot Cycle’s Diagrams
The Carnot cycle is an ideal thermodynamic cycle consists of four reversible processes (Figures 3 and 4): isothermal expansion, adiabatic expansion (so as reversible isentropic) isothermal compression and adiabatic compression. This is the most efficient cycle to get work from two sources of heat constant temperatures; the reverse cycle is the most efficient way to transfer heat from a cold source to a hot source from a work source. The effectiveness of other cycles and real machines is compared to that of the Carnot cycle through the performance, a dimensionless number between 0 (zero efficiency) and 1 (perfect efficiency) characterizes that effectiveness. One of the objectives of this paper is to remember that, contrary to what is taught until now; the hot air is not always lighter than cold air throughout the troposphere. Indeed there is a region between the surfaces rating restively at 6.11 mb and 0.0098˚C, in which the cold updrafts and warm downdrafts are thermodynamically authorized (Figure 2). Updrafts observed over cumulonimbus’ cold downdrafts can now be understood.
3.2. Thermodynamic Sizes of Hadley Cells Derived from Tornadoes’ Clouds
Vertical sizes of Hadley cells are revealed by vertical profile of low troposphere clouds (N.B.: clouds are for our eyes, tracers of the wind’s streamlines) that accompany the formation of Tornadoes. Indeed, Tornadoes involves vertical velocity (w) significantly higher than those involved in the formation of Hadley cells (where w ≈ 0), and all the photos (Figures 5(a) and (d)) of these

Figure 1. Saturation curves for water substance onto the pT-plane (pT and TT are called triple-point data): ewT = 6.11 mb; TT = 0.0098˚C.

Table 1. Pressure variation of a constant volume of moist air, depending on the temperature T: in specific regions of the troposphere, delimited by equal level surfaces rating respectively at 0.0098˚C and 6.11 mb.
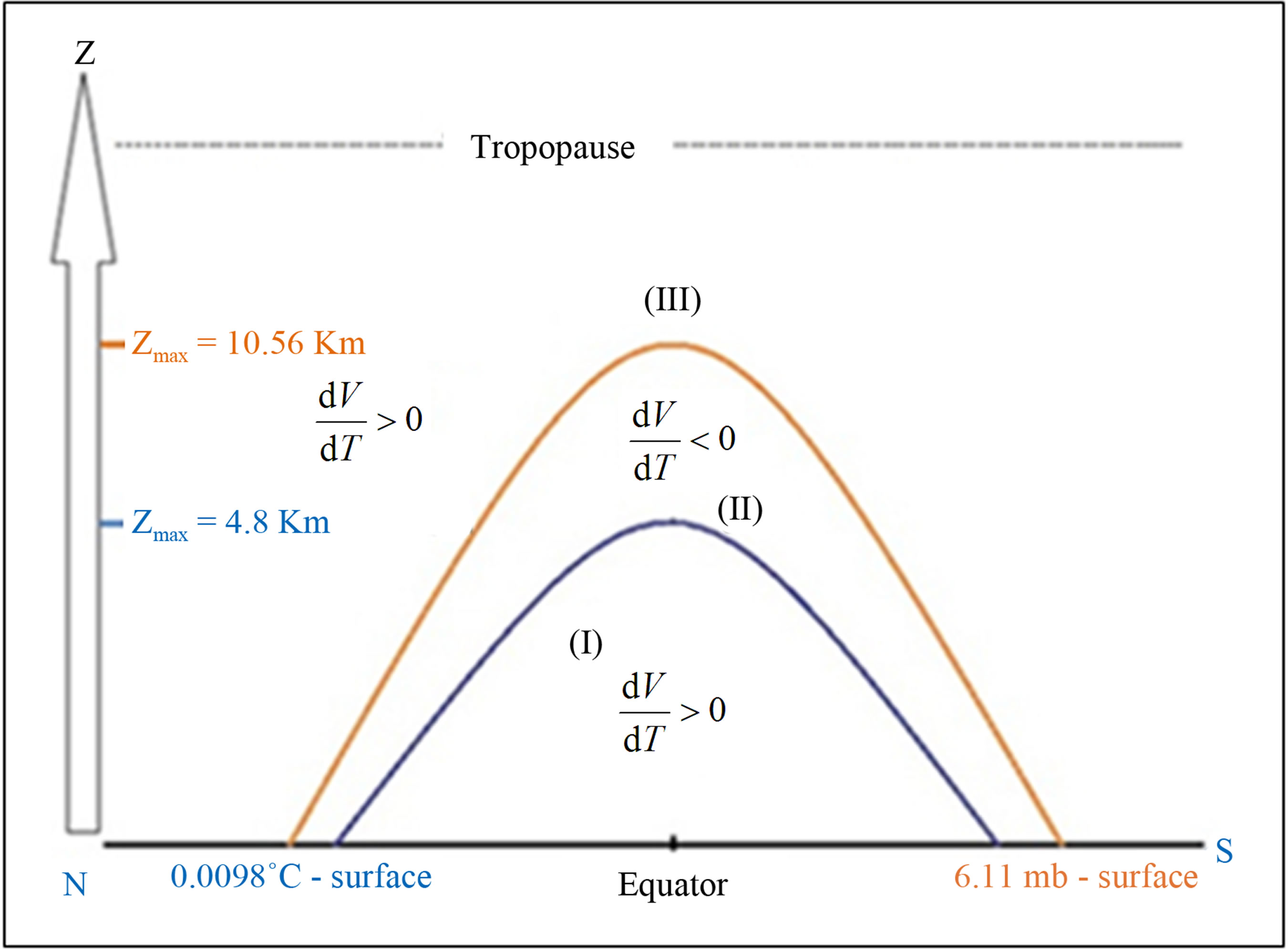
Figure 2. Troposphere specific regions depending on the manner in which V changes with T (V and T are respectively volume and temperature of an air parcel): (dV/dT) > 0; the particle swells when its temperature increases (so it becomes lighter); (dV/dT) < 0 the particle shrinks when its temperature increases (so it becomes less light).
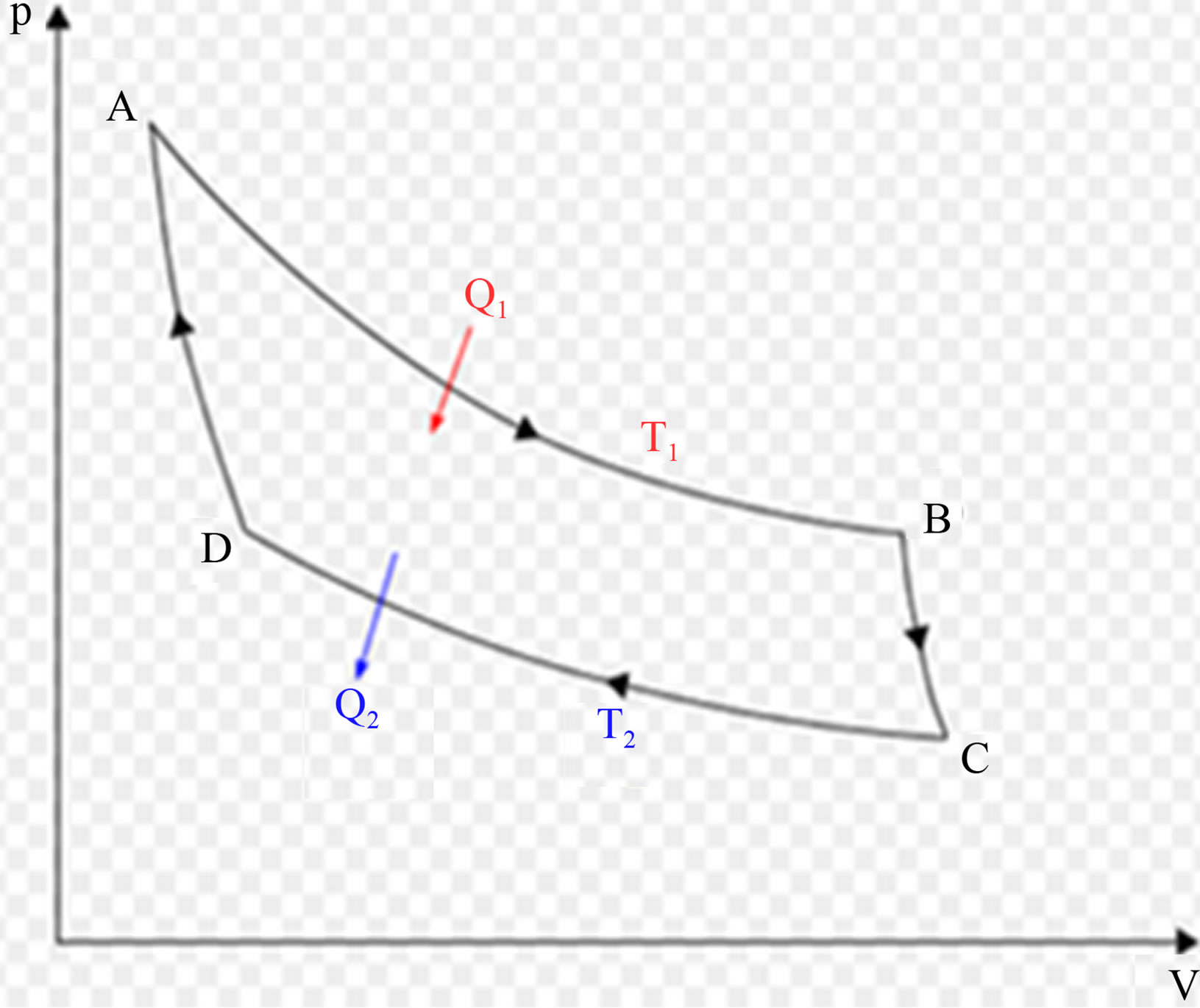
Figure 3. Carnot Cycle in pV-diagram. A-B: isothermal expansion; B-C: adiabatic expansion; C-D: isothermal compression; D-A: adiabatic compression
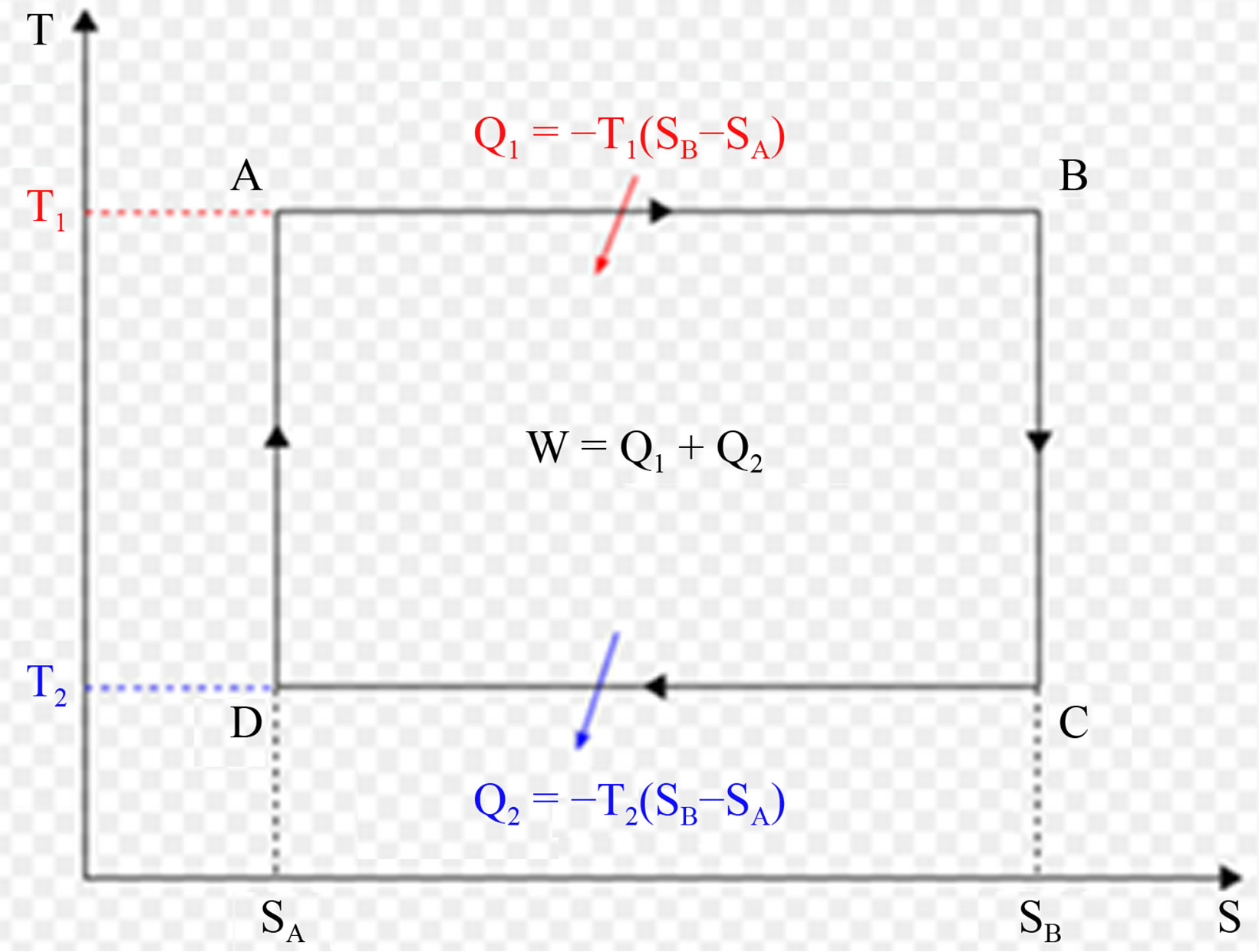
Figure 4. Carnot Cycle in TS-diagram.
clouds (whose bases are crowded near the ground by numerous kind of debris) show that: the lower troposphere warm updrafts are inevitably stopped by a physical process stayed well below the tropopause. According to Clausius-Clapeyron relation delivered in paragraph (2), that physical process is the first reversal of deep and passive convection vertical movements which takes place at the 0.0098˚C isotherm. Furthermore the cloud formation in the lower troposphere is indicative of adiabatic expansion that under the Carnot cycle requirements delivered in paragraph (3.1.) must be immediately followed by an isothermal compression. Hence this low-troposphere cloud’s horizontal spreading which reveals the beginning of the descent of convective cells to lower altitudes.
These thermodynamic and kinematic proofs (tornadoes’ clouds profile; Clausius-Clapeyron saturation curves for water substance onto the pT-plane and Carnot Cycle configuration) are irrefutable and lead to conclusive evidence that the 0.0098˚C isotherm overlooks the Hadley cells (Figure 6(a)) contrary to what is shown in Figures 6(b) and (c).
4. Conclusion
Using the ideal gas approximation, without first making the necessary checks was from the founding fathers of modern meteorology (George Hadley (1735), Tor Bergeron (1959), William Ferrel (1860)), a fatal error. Indeed their successive representations of general circulation have suffered from this blunder. Nobody, however, can blame the founding fathers because they have promoted meteorology in several areas and that their availa-

Figure 5. (a)-(d) Tornadoes are like little-bombs triggered by cloud’s additional greenhouse (Mbane, 2013). Indeed, Rayleigh and Reynolds numbers of passive convection motions depend mainly on air parcel temperature and humidity. Within additional greenhouse, temperature and water vapor increase exponentially and finally (as atmosphere is a dissipative system) trigger violent adiabatic expansion or tornadoes (as Rayleigh and Reynolds numbers become higher and generate turbulent motions).
 (a)
(a)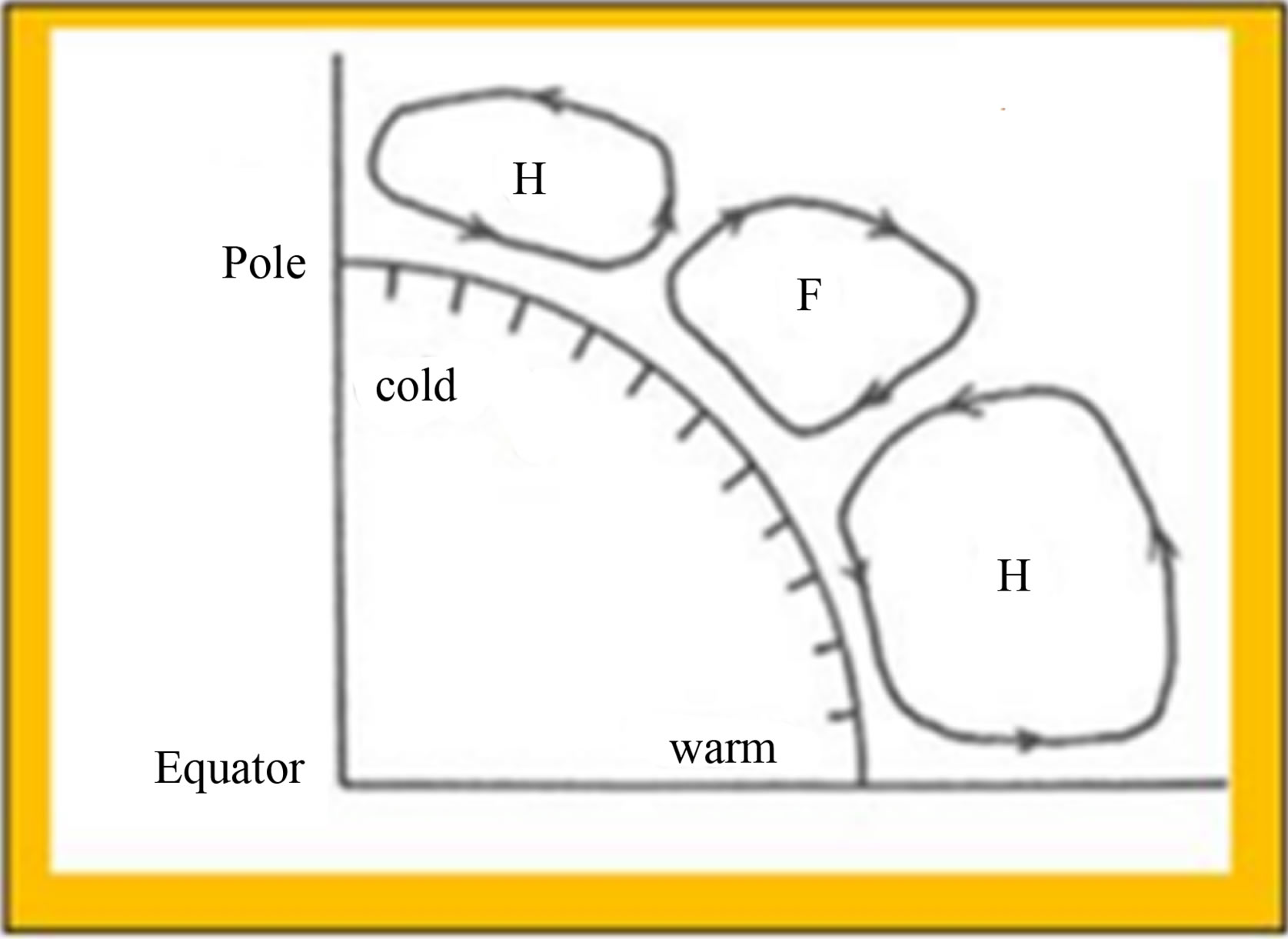 (b)
(b)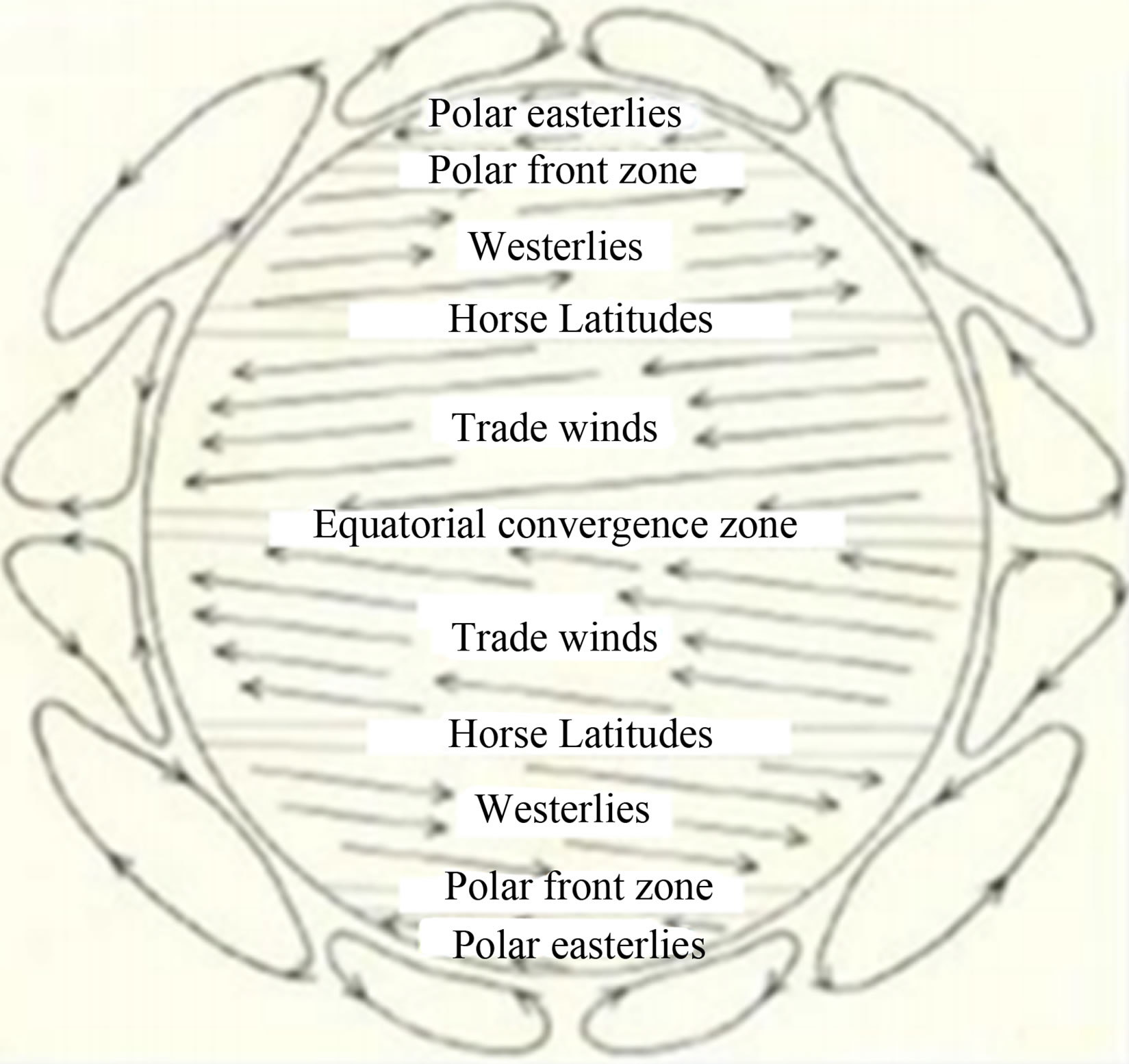 (c)
(c)
Figure 6. (a) Schematic representation of the general circulation based on troposphere dynamic balance; (b) Schematic illustration of the observed hemispheric mean meridional Circulation C. A. Riegel [27]; (c) Schematic representation of the general circulation, modified after Bergeron and Rossby (H. R. Byers, 1959).
ble observations did not allow doubt about the ideal gas approximation. Now, doubts are no longer allowed and efforts should be made to rectify many of the misinterpretations, which abound in meteorology. Meteorologists can benefit greatly from advances in fluid mechanics and thermodynamics. One of the goals of this work is to encourage more collaboration between meteorologists and physicists.
REFERENCES
- C. Mbane Biouele, “Hurricanes and Cyclones Kinematics and Thermo-Dynamics Based on Clausius-Clapeyron Relation Derived in 1832,” International Journal of Physical Sciences, Vol. 8, No. 23, 2013, pp. 1284-1290.
- C. Mbane Biouele, E. Yizengaw, M. B. Moldwin and G. Cautenet, “Impacts of Thermoelastic Properties of Saturated Water Vapor on Tropical Depressions Thermodynamics and Dynamics,” Arch. Phys.Rech., Vol. 2, No. 4, 2011, pp. 24-33.
- C. Mbane Biouele, “Vertical Profi-les of Winds and Electric Fields Triggered by Tropical Storms under the Hydrodynamic Concept of Air Particle,” International Journal of Physical Sciences, Vol. 4, No. 4, 2009, pp. 242- 246.
- C. Mbane Biouele, “Physics of Atmosphere Dynamic or Electric Balance Processes Such As Thunderclouds and Related Lighting Flashes,” Geosciences, Vol. 2, No. 1, 2012, pp. 6-10.
- M. Steiner and R. A. Houze Jr., “Sensitivity of the Estimated Monthly Convective Rain Fraction to the Choice of Z-R Relation,” Journal of Applied Meteorology, Vol. 36, No. 5, 1997, pp. 452-462.
- R. A. Houze Jr., “Cloud Clusters and Large-Scale Vertical Motions in the Tropics,” Journal of the Meteorological Society of Japan, Vol. 60, No. 1, 1982, pp. 396-410.
- B. E. Mapes and R. A. Houze Jr., “Cloud Clusters and Superclusters over the Oceanic Warm Pool,” Monthly Weather Review, Vol. 121, No. 5, 1993, pp. 1398-1415. http://dx.doi.org/10.1175/1520-0493(1993)121<1398:CCASOT>2.0.CO;2
- D. L. Hartmann, H. H. Hendon and R. A. Houze Jr., “Some Implications of the Mesoscale Circulations in Tropical Cloud Clusters for Large-Scale Dynamics and Climate,” Journal of the Atmospheric Sciences, Vol. 41, No. 1, 1984, pp. 113-121.
- D. A. Short and K. Nakamura, “TRMM Radar Observations of Shallow Precipitation over the Tropical Oceans,” Journal of Climate, Vol. 13, No. 23, 2000, pp. 4107- 4124. http://dx.doi.org/10.1175/1520-0442(2000)013<4107:TROOSP>2.0.CO;2
- C. Prabhakara, R. Iacovazzi, J. A. Weinman and G. Dalu, “A TRMM Microwave Radiometer Rain Rates Estimation Method with Convective and Stratiform Discrimination,”Journal of the Meteorological Society of Japan, Vol. 78, No. 3, 2000, pp. 241-258.
- Z. D. Adeyewa and K. Nakamura, “Preliminary Study of Rainfall and Storm Structure over Africa with TRMM Precipitation Radar Data,” Meteorologische Zeitschrift, Vol. 12, No. 4, 2003, pp. 197-202. http://dx.doi.org/10.1127/0941-2948/2003/0012-0197
- Z. D. Adeyewa and K. Nakamura, “Validation of TRMM Radar Rainfall Data over Major Climatic Regions in Africa,” Journal of Applied Meteorology, Vol. 42, No. 2, 2003, pp. 331-347.
- R. J. Donaldson, “Radar Reflectivity Profiles in Thunderstorms,” Journal of Meteorology, Vol. 18, No. 3, 1961, pp. 292-305. http://dx.doi.org/10.1175/1520-0469(1961)018<0292:RRPIT>2.0.CO;2
- E. J. Zipser and K. R. Lutz, “The Vertical Profile of Radar Reflectivity of Convective Cells: A Strong Indicator of Storm Intensity and Lightning Probability” Monthly Weather Review, Vol. 122, No. 8, 1994, pp. 1751-1759. http://dx.doi.org/10.1175/1520-0493(1994)122<1751:TVPORR>2.0.CO;2
- C. Kummerow, et al., “The Status of the Tropical Rainfall Measuring Mission (TRMM) after Two Years in Orbit,” Journal of Applied Meteorology, Vol. 39, No. 12, 2000, pp. 1965-1982.
- F. Ferreira, P. Amayenc, S. Oury and J. Testud, “Study and “Tests of Improved Rain Estimates from the TRMM Precipitation Radar,” Journal of Applied Meteorology, Vol. 40, No. 11, 2001, pp. 1878-1899.
- C. Kummerow and L. Giglio, “A Passive Microwave Technique for Estimating Rainfall and Vertical Structure Information from Space. Part 1: Algorithm Description,” Journal of Applied Meteorology, Vol. 33, No. 1, 1994, pp. 3-18. http://dx.doi.org/10.1175/1520-0450(1994)033<0003:APMTFE>2.0.CO;2
- S. Lang, W. K. Tao, J. Simpson and B. Ferrier, “Modeling of Convective-Stratiform Precipitation Processes: Sensitivity to Partitioning Methods,” Journal of Applied Meteorology, Vol. 42, No. 4, 2003, pp. 505-527. http://dx.doi.org/10.1175/1520-0450(2003)042<0505:MOCSPP>2.0.CO;2
- Y. Hu and Q. Fu, “Observed Poleward Expansion of the Hadley Circulation since 1979,” Atmospheric Chemistry and Physics, Vol. 7, 2007, pp. 5229-5236.
- J. Lu, G. A. Vecchi and T. Reichler, “Expansion of the Hadley Cell under Global Warming,” Geophysical Research Letters, Vol. 34, 2007, Article ID: L06805. http://dx.doi.org/10.1029/2006GL028443
- R. W. Hobbs and M. N. Raphael, “Characterizing the Zonally Asymmetric Component of the SH Circulation,” Climate Dynamics, Vol. 35, 2010, pp. 859-873.
- P. Kushner, I. M. Held and T. L. Delworth, “Southern Hemisphere Atmospheric Circulation Response to Global Warming,” Journal of Climate, Vol. 14, No. 10, 2001, pp. 2238-2249. http://dx.doi.org/10.1175/1520-0442(2001)014<0001:SHACRT>2.0.CO;2
- L. Polvani and P. J. Kushner, “Tropospheric Response to Stratospheric Perturbations in a Relatively Simple General Circulation Model,” Geophysical Research Letters, Vol. 29, No. 7, 2002, 18 p. http://dx.doi.org/10.1029/2001GL014284
- L.-M. Polvani, D. W. Waugh, G. J. P. Correa and S.-W. Son, “Stratospheric Ozone Depletion: The Main Driver of Twentieth-Century Atmospheric Circulation Changes in the Southern Hemisphere,” Journal of Climate, Vol. 24, 2011, pp. 795-812.
- H. R. Byers, “General Meteorology,” McGraw-Hill Book Company. INC, 1959, 540 p.
- G. K. Batchelor, “An Introduction to Fluid Dynamics,” Cambridge University Press, 1967, 496 p.
- C. A. Riegel, “Fundamentals of Atmospheric Dynamics and Thermo-Dynamics,” World Scientific Publishing Co. Pte. Ltd., 1992, 512 p.

