ABSTRACT

The optimizing total velocity increment 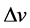needed for orbital maneuver between two elliptic orbits with plane change is investigated. Two-impulse orbital transfer is used based on a changing of transfer velocities concept due to the changing in the energy. The transferring has been made between two elliptic orbits having a common centre of attraction with changing in their planes in standard Hohmann transfer with the terminal orbit which is elliptic orbit and not circular. We develop a treatment based on the elements of elliptic orbits, 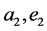and 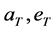of the initial orbit, final orbit and transferred orbit respectively. The first impulse at the perigee induces a rotation of the orbital plane by 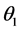which will be minimized. The second impulse 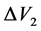at apogee is induced an angle 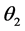to product the final elliptic orbit. The total plane change required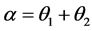. We calculate the total impulse 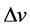and minimize by optimizing angle of plane’s variation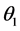. We obtain a polynomial equation of six degrees on the two transfer angles between neither two elliptic orbits 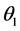and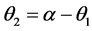. The solution obtained numerically, using programming code of MATHEMATICA V10, with no condition on the eccentricity or the semi-major axis of the initial, transformed, and the final orbits. We find that there are constrains on the transfer angles 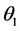and. 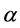For 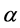it must be between 40˚ and 160˚, and there is no solution if 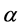is less than 40˚ and bigger than 160˚ and 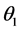takes the values less than 40˚. The minimum total velocity increments obtained at the value of 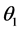less than 25^o and equal to 160˚. This is an interesting result in orbital transfer problem in which the change of orbital plane is necessary for the transferring.

Keywords:

Orbital Mechanics, Astrodynamics, Optimization, Elliptic Hohmann Transfer

1. Introduction

The problem of the optimal impulsive transfer between two orbits is almost seventy years old, but the question, how many impulses are still open despite of the theories and a lot of numerical works developed in this field. In 1925, Hohmann produced a numerical study showing that the optimum two-impulse transfer path between coplanar circular orbits is a semi-ellipse, tangential at its apsides to both circular orbits, with an impulse occurring at each apse. Hohmann transfer is generalized to the elliptic case (transfer between two coaxial elliptic orbits). A large number of works have been made to optimize non-coplanar transfer between circular or elliptic orbits having collinear major axes [1] [2] [3] [4] . An analytical solution for optimal two-impulse 180˚ transfer between non-coplanar elliptic orbits and the optimal orientation of the transfer plane is presented with numerical solutions under some terminal conditions in [5] . A polynomial equation of six degrees on the generalized Hohmann transfer with plane change using energy concepts is obtained without analytical solution [6] . A fundamental result is presented in Lawden’s work where a primer vector satisfying necessary condition for optimality of the total delta velocity was introduced in coplanar transfer [7] . The necessary condition for optimality is reduced to a polynomial equation of the eighth degrees on the semi-latus rectum and with the fixed transfer angle, for which no solution has been found in two-impulse transfer between two elliptic coplanar orbits [8] . In this work, we give the optimum total velocity increment required to transfer between two elliptic orbits having a common centre of attraction with plane change. We considered here generalized Hohmann transfer consisted of two impulses through semi-elliptic path. The first thrust occurring at the perigee does not only produce a transfer ellipse but also induce a rotation of the orbital plane by. The second impulse at apogee is induced an angle to produce the final elliptic orbit. An engine firing in the out of plane direction is required for the change of the plane. The point of firing becomes a point in the new orbit, and the burn point becomes the intersection of the current orbit and the desired orbit. In the following treatment, we used a changing of transfer velocities concept due to the changing in the energy in terms of the elliptic orbital elements, and of the initial orbit, final orbit and transferred orbit respectively. We calculate the total impulse and minimize by optimizing angle of plane’s variation, we obtain a polynomial equation of six degrees on the two transfer angles between neither two elliptic orbits and with any restrictions on their eccentricities and semi-major axis, nor any restrictions on the terminal distances and the initial and final orbital velocities. The solution obtained numerically, using programming code of MATHEMATICA V10. The total velocity impulse is minimized by optimizing angle of plane’s variation numerically under some constrains of the transfer angles.

2. Formulation and Optimization

Any analysis of orbital maneuvers, i.e., the transfer of a satellite from one orbit to another by means of a change in velocity, begins with the energy as

(1)

where is the magnitude of the orbital velocity at some point, the magnitude of the radius from the focus to that point, a semi major axis of the orbit and the gravitational constant of the attracting body. Equation (1) can be rearranged as

(2)

where it is evident that

Note that (energy/satellite mass (is dependent only on a, an increases, energy increases. Orbital maneuvers are based on the principle that an orbit is uniquely determined by the position and velocity vector at any point [9] . Conversely, changing the velocity vector at any point instantly transforms the trajectory to a new one corresponding to the new velocity vector. So if we want to move a spacecraft to a higher orbit, we have to increase the semi-major axis (adding energy to the orbit) by increasing velocity. On the other hand, to move the spacecraft to a lower orbit, we decrease the semi-major axis (and the energy) by decreasing the velocity. Any conic orbit can be transformed into another conic orbit by changing the spacecraft velocity vector. Coplanar maneuver only involves the change of the orbit without changing the orbit plane, we have four kind of coplanar maneuvers (i) Tangential orbit Maneuver, (ii) Non-tangential orbit Maneuver, (iii) Hohmann transfer, (iv) Bi-elliptic orbit transfer. The Hohmann’s transfer is the minimum two-impulse transfer between coplanar circular or elliptic, it can be used to transfer a satellite between two nonintersecting orbits, coaxial, aligned. The fundamental of the Hohmann’s transfer is a simple maneuver. This maneuver employs an intermediate elliptic orbit which is tangent to both initial and final orbits at their apsides. A maneuver (refers to the difference between the initial and final velocity vectors),can raise or lower the perigee or apogee, a change in inclination, escape, reduction or increase in period, begin a 2+ maneuver sequence of burns. This process takes two steps, to get from orbit one to the transfer orbit, we change the orbit’s energy by changing the spacecraft’s velocity by an amount. Then when the spacecraft gets to orbit two, we must change its energy again by changing its velocity by an amount, if we don’t the spacecraft will remain in the transfer orbit, indefinitely, returning to where it started in orbit one, then back to orbit two, etc. Thus, the complete maneuver requires two separate energy changes, accomplished by changing the orbital velocities (using and). For mission planning, we simply add the needed for the trip from orbit one to orbit two. Now we have gone through the Hohmann transfer, when the transfer between two elliptic non aligned orbits, for an example the spacecraft went from a low orbit to a higher orbit or vice versa with different planes, to do this, it had to increase velocity twice, and. At the point, we apply an impulse with magnitude increase the spacecraft’s velocity, taking the spacecraft out of orbit one and putting it into the transfer orbit, the transfer orbit crosses the final orbit at the point, where we apply an impulse with magnitude putting it into the final orbit as in Figure 1. At point, is the perigee distance of orbit one (The initial orbit with an elements,) and and at the point, is the apogee distance of orbit two (The final orbit with an elements,) and. The transfer orbit given by an elements and, where

(3)

(4)

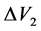
The total velocity increment will obtain from the following relations, as seen in Figure 2.

(5)

(6)

where, , , and are the perigee velocity at of the initial orbit, the transfer’s velocity of the transfer orbit at perigee, the apogee velocity at of the final orbit and the transfer’s velocity of the transfer orbit at apogee respectively.

;

;

and are the angles between the velocities at and as shown in Figure 1, and. So Equations ((5) and (6)) will be

(7)

(8)

Thus, the total increment of the velocity is

(9)

For simplicity let

, , , (10)

Then (9) will be in the form

(11)

to be optimized by the condition of minimization

By partial differentiation of (11) with respect to and equating to zero, and after arrangements and clearing fraction, we find that

(12)

From which we can deduce that

(13)

where

, , , (14)

After some reduction, we find that

Let

Then

(15)

After squaring and some reduction, we may write

(16)

Set

Then Equation (16) will be an algebraic equation of degree six in (with explicitly) in the form

(17)

3. Solution and Discussion

There is no analytical solution for the Equation (17), but we solved it numerically, using code of MATHEMATICA V10, with no condition on the eccentricity or the semi-major axis of the initial, transformed, and the final orbits. The optimization problem was solved for two angles of rotation of the apsidal lines, using the computed values of the velocities at perigee and apogee, and the transfer angle. The necessary optimal conditions are obtained using analytical code and different numerical code by MATHEMATICA V10. For each value of eccentricities, and semi-majors, we find at least one root satisfied Equation (17). Also we find that there is constrains on the transfer angles and as seen in Table 1 and Figure 3. For it must be between 40˚ and 160˚, there is no solution if is less than 40˚ and bigger than 160˚. Also the minimum total velocity increments will obtain with the value of less than 40˚ and less than 160˚. This is an interesting result in orbital transfer problem in which the change of orbital plane is necessary for the transferring.

4. Conclusion

We give a complete analytical analysis and numerical solution of optimal two-

impulse transfer with plane change. Our treatment is based on a changing of transfer velocities concept due to the changing in the energy. We obtained the total velocity increment of the two impulses and at perigee and apogee respectively, in terms of the semi-major axes and the eccentricities of the initial orbit, final orbit and transferred orbit respectively. The transferring has been made between two elliptic orbits having a common centre of attraction with changing in their planes in a tight Hohmann’s transfer with the terminal orbit which is elliptic orbit. We minimized by optimizing angle of plane’s variation. We obtain a polynomial equation of six degrees on the two transfer angles between neither two elliptic orbits and. The optimization process here depends on the value of the plane change with no constrain on a or e, the optimal maneuver can be purely propulsive. It is shown that whenever an impulse is applied, a plane change is made. The necessary conditions for the optimal split of the plane changes are derived and simulated in computer program for the solution. We optimized with new constrains in the angles of transfer, for it must be between 40˚ and 160˚ and there is no solution if is less than 40˚ and bigger than 160^o, takes the values less than 40˚. The minimum total velocity increments obtained at the value of less than 25˚ and equal to 160˚. This constrains are newer and more different than which are obtained in others works [3] [4] [5] . This is an interesting result in orbital transfer problem in which the change of orbital plane is necessary for the transferring.

Cite this paper

Youssef, M.H.A. (2017) The Solution of Optimal Two-Impulse Transfer between Elliptical Orbits with Plane Change. International Journal of Astronomy and Astrophysics, 7, 125-132. https://doi.org/10.4236/ijaa.2017.73010

References