International Journal of Astronomy and Astrophysics
Vol.07 No.02(2017), Article ID:75360,17 pages
10.4236/ijaa.2017.72005
Existence of Equilibrium Points in the R3BP with Variable Mass When the Smaller Primary is an Oblate Spheroid
M. R. Hassan1, Sweta Kumari2, Md. Aminul Hassan3
1Department of Mathematics, S. M. College, T. M. Bhagalpur University, Bhagalpur, India
2Research Scholar, T. M. Bhagalpur University, Bhagalpur, India
3GTE, Bangalore, India
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 25, 2017; Accepted: April 9, 2017; Published: April 12, 2017
ABSTRACT
The paper deals with the existence of equilibrium points in the restricted three-body problem when the smaller primary is an oblate spheroid and the infinitesimal body is of variable mass. Following the method of small parameters; the co-ordinates of collinear equilibrium points have been calculated, whereas the co-ordinates of triangular equilibrium points are established by classical method. On studying the surface of zero-velocity curves, it is found that the mass reduction factor has very minor effect on the location of the equilibrium points; whereas the oblateness parameter of the smaller primary has a significant role on the existence of equilibrium points.
Keywords:
Restricted Three-Body Problem, Jean’s Law, Space-Time Transformation, Oblateness, Equilibrium Points, Surface of Zero-Velocity

1. Introduction
Restricted problem of three bodies with variable mass is of great importance in celestial mechanics. The two-body problem with variable mass was first studied by Jeans [1] regarding the evaluation of binary system. Meshcherskii [2] assumed that the mass was ejected isotropically from the two-body system at very high velocities and was lost to the system. He examined the change in orbits, the variation in angular momentum and the energy of the system. Omarov [3] has discussed the restricted problem of perturbed motion of two bodies with variable mass. Following Jeans [1] , Verhulst [4] discussed the two body problem with slowly decreasing mass, by a non-linear, non-autonomous system of differential equations. Shrivastava and Ishwar [5] derived the equations of motion in the circular restricted problem of three bodies with variable mass with the assumption that the mass of the infinitesimal body varies with respect to time.
Singh and Ishwar [6] showed the effect of perturbation on the location and stability of the triangular equilibrium points in the restricted three-body problem. Das et al. [5] developed the equations of motion in elliptic restricted problem of three bodies with variable mass. Lukyanov [7] discussed the stability of equilibrium points in the restricted problem of three bodies with variable mass. He found that for any set of parameters, all the equilibriums points in the problem (Collinear, Triangular and Coplanar) are stable with respect to the conditions considered in the Meshcherskii space-time transformation. El Shaboury [8] discussed the equation of motion of Elliptic Restricted Three-body Problem (ER3BP) with variable mass and two triaxial rigid bodies. He applied the Jeans law, Nechvili’s transformation and space-time transformation given by Meshcherskii in a special case.
Plastino et al. [9] presented techniques for the problems of Celestial Mechanics, involving bodies with varying masses. They have emphasized that Newton’s second law is valid only for the body of fixed masses and the motion of a body losing mass is isotropically unaffected by this law. Bekov [10] [11] has discussed the equilibrium points and Hill’s surface in the restricted problem of three bodies with variable mass. He has also discussed the existence and stability of equilibrium points in the same problem. Singh et al. [12] has discussed the non-linear stability of equilibrium points in the restricted problem of three bodies with variable mass. They have also found that in non-linear sense, collinear points are unstable for all mass ratios and the triangular points are stable in the range of linear stability except for three mass ratios which depend upon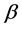 , the constant due to the variation in mass governed by Jean’s law.
, the constant due to the variation in mass governed by Jean’s law.
At present, we have proposed to extend the work of Singh [12] by considering smaller primary as an oblate spheroid in the restricted problem of three bodies as shown in Figure 1 and to find the co-ordinates of equilibrium points 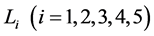 by the method of small parameters.
by the method of small parameters.
2. Equations of Motion
Let 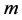 be the mass of the infinitesimal body varying with time. The primaries of masses
be the mass of the infinitesimal body varying with time. The primaries of masses 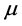 and
and 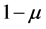 are moving on the circular orbits about their centre of mass as shown in Figure 1. We consider a bary-centric rotating co-ordinate system
are moving on the circular orbits about their centre of mass as shown in Figure 1. We consider a bary-centric rotating co-ordinate system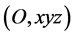 , rotating relative to inertial frame with angular velocity
, rotating relative to inertial frame with angular velocity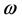 . The line joining the centers of
. The line joining the centers of 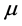 and
and 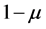 is considered as the
is considered as the 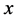 -axis and a line lying on the plane of motion and perpendicular to the
-axis and a line lying on the plane of motion and perpendicular to the 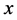 -axis and through the centre of mass as the
-axis and through the centre of mass as the 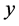 -axis and a line through the centre of mass and perpendicular to the plane of motion as the
-axis and a line through the centre of mass and perpendicular to the plane of motion as the 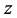 -axis. Let
-axis. Let 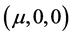 and
and 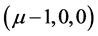 respectively be the co-ordinates of the primaries
respectively be the co-ordinates of the primaries 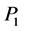 and
and 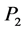 and
and 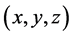 be the co-ordinates of the infinitesimal mass
be the co-ordinates of the infinitesimal mass

Figure 1. Rotating frame of reference in the R3BP in 3-Dimension about Z-axis.

where

The oblateness parameter of the smaller primary is given by

where 



and
Now from Equation (1),


where units are so chosen that the sum of the masses of the primaries and the gravitational constant 
The equations of motion in the Cartesian form are

where

i.e.,

By Jeans law, the variation of mass of the infinitesimal body is given by

where 

Let us introduce space time transformations as

where 

From Equations ((7) and (8)), we get

where

Differentiating 


Also,
Now,
Putting the values of 


where

In order to make the Equation (10) free from the non-variational factor, it is sufficient to put

Thus the System (10) reduces to

where

From System (13),

The Jacobi’s Integral is

3. Existence of Equilibrium Points
For the existence of equilibrium points 
For solving the above equations, let us change these equations in Cartesian form as

4. Existence of Collinear Equilibrium Points
For the Collinear equilibrium points, 

From Equation (17), we get

Let 


Thus from Equation (18),

as


For the first equilibrium point

Here, Equation (20) is seven degree polynomial equation in



Figure 2. Locations of collinear and triangular equilibrium points.
Thus



Thus the Equation (20) reduces to

Let 


Putting the value of 


where
Therefore, the co-ordinate of the first equilibrium point 

Let 


Thus from Equation (18),

Since 

where 
In terms of
i.e.,

The Equation (26) is a seven degree polynomial equation in

If we put 

Here 




where
Let 





where
Thus the co-ordinate of the second equilibrium point is given by
Let 
Thus from Equation (18), we have

When




Let
where 
Thus Equation (29) reduced to
By putting values of 


where
Thus the co-ordinates of the third equilibrium point is given by
5. Existence of Triangular Equilibrium Points
For triangular equilibrium point 



Now 

Again 

Since

For better approximation



For triangular equilibrium points

Now,

Again,

Putting the value of 





Thus,

Therefore,


6. Surface of Zero?Velocity
Figure 3. Zero velocity curve (ZVC) for 
Figure 4. Zero velocity curve for 
Figure 5. Zero velocity curve for 
Figure 6. Zero velocity curve for 
Figure 7. Zero velocity curve for 
Figure 8. Zero velocity curve (ZVC) for 
Figure 9. 3 Dimensional view of ZVC of Figure 6.
Figure 10. 3 Dimensional view of ZVC of Figure 7.
Figure 11. 3 Dimensional view of ZVC of Figure 8.
7. Discussions and Conclusions
In section 2, the equations of motion of the infinitesimal body with variable mass have been derived under the gravitational field of one oblate primary and other spherical. By Jean’s law, the time rate mass variation is defined as


in which exponent of the mass of the stars of the main sequence lies. The System (4) is transformed to space-time co-ordinates by the space-time transformations given in Equations (8) and (9). The Jacobi’s integral has been derived in Equation (16).
In section 3, the equations for solving equilibrium points, have been derived in Equation (17) by putting 


co-ordinates of 


the co-ordinates of equilateral triangular equilibrium points have been calculated by the classical method. In section 6, zero-velocity curves in Figures 3-8 and its 3-dimensional surface in Figures 9-11 have been drawn for 

From the above facts we concluded that in the perturbed case, first equilibrium point 












Cite this paper
Hassan, M.R., Kumari, S. and Hassan, Md.A. (2017) Existence of Equilibrium Points in the R3BP with Variable Mass When the Smaller Primary is an Oblate Spheroid. International Journal of Astronomy and Astrophysics, 7, 45-61. https://doi.org/10.4236/ijaa.2017.72005
References
- 1. Jeans, J.H. (1928) Astronomy and Cosmogony. Cambridge University Press, Cambridge.
- 2. Meshcherskii, L.V. (1949) Studies on the Mechanics of Bodies of Variable Mass, Gostekhizdat, Moscow.
- 3. Omarov, T.B. (1963) The Restricted Problem of Perturbed Motion of Two Bodies with Variable Mass. Soviet Astronomy, 8, 127.
- 4. Verhulst, F. (1972) Two-Body Problem with Slowly Decreasing Mass. Celestial Mechanics and Dynamical Astronomy, 5, 27-36.
https://doi.org/10.1007/bf01227820 - 5. Das, R.K., Shrivastav, A.K. and Ishwar, B. (1988) Equations of Motion of Elliptic Restricted Problem of Three Bodies with Variable Mass. Celestial Mechanics and Dynamical Astronomy, 45, 387-393.
https://doi.org/10.1007/BF01245759 - 6. Shrivastava, A.K. and Ishwar, B. (1983) Equations of Motion of the Restricted Problem of Three Bodies with Variable Mass. Celestial Mechanics and Dynamical Astronomy, 30, 323-328.
https://doi.org/10.1007/BF01232197 - 7. Lukyanov, L.G. (1990) The Stability of the Libration Points in the Restricted Three-Body Problem with Variable Mass. Astronomical Journal, 67, 167-172.
- 8. El-Shaboury, S.M. (1990) Equations of Motion of Elliptically-Restricted Problem of a Body with Variable Mass and Two Tri-Axial Bodies. Astrophysics and Space Science, 174, 291-296.
https://doi.org/10.1007/BF00642513 - 9. Plastino, A.R. and Muzzio, J.C. (1992) On the Use of and Abuse of Newton’s Second Law for Variable Mass Problems. Celestial Mechanics and Dynamical Astronomy, 53, 227-232.
https://doi.org/10.1007/BF00052611 - 10. Bekov, A.A. (1993) The Libration Points and Hill Surfaces in the Restricted Problem of Three Variable Mass Bodies. Proceedings of the International Astronomical Union Colloquium 132, New Delhi, 10-13 October 1993, 277-288.
https://doi.org/10.1017/S0252921100066173 - 11. Bekov, A.A. (1993) Problem of Physics of Stars and Extragalactic Astronomy. 91-114.
- 12. Singh, J. and Ishwar, B. (1985) Effect of Perturbations on the Stability of Triangular Points in the Restricted Problem of Three Bodies with Variable Mass. Celestial Mechanics and Dynamical Astronomy, 35, 201-207.
https://doi.org/10.1007/bf01227652





































