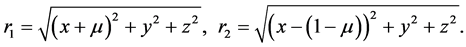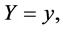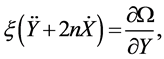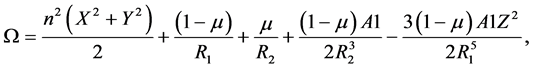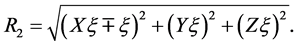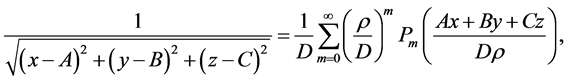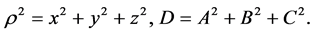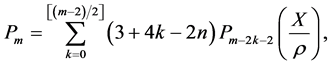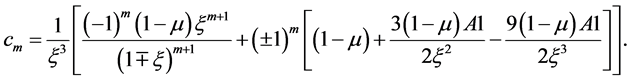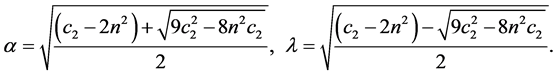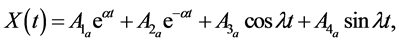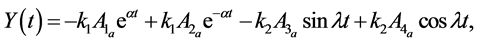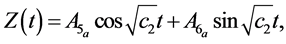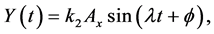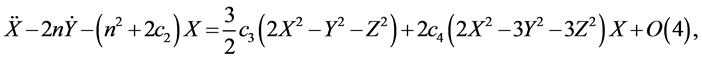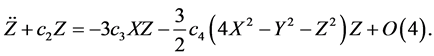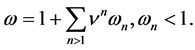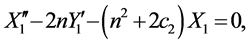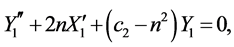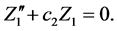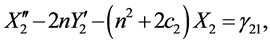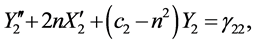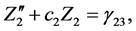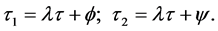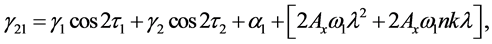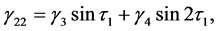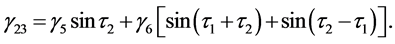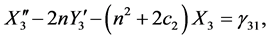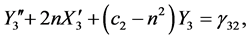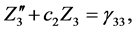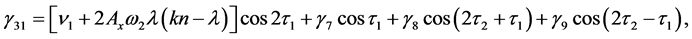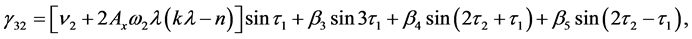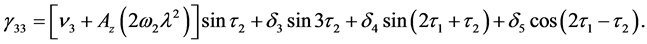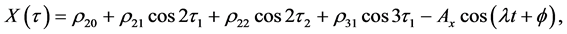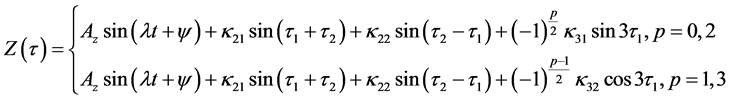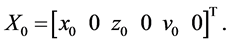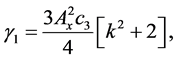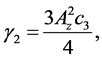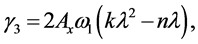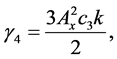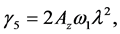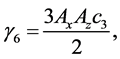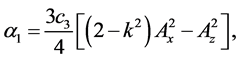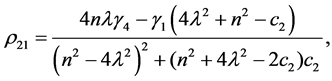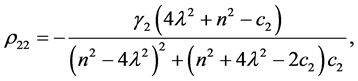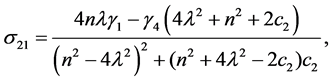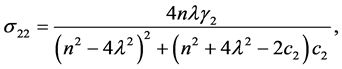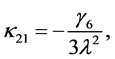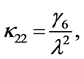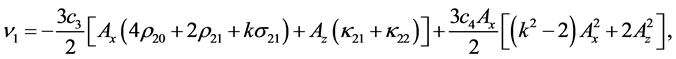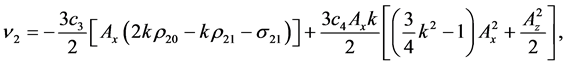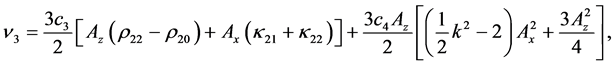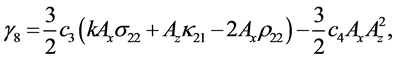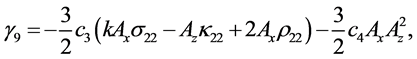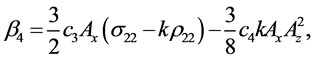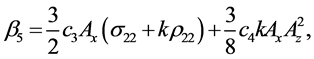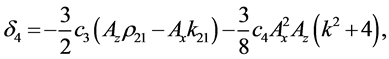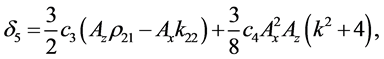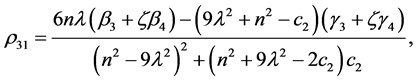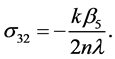International Journal of Astronomy and Astrophysics
Vol.06 No.04(2016), Article ID:71856,31 pages
10.4236/ijaa.2016.64029
Oblateness Effect of Saturn on Halo Orbits of L1 and L2 in Saturn-Satellites Restricted Three-Body Problem
Nishanth Pushparaj, Ram Krishan Sharma
Department of Aerospace Engineering, Karunya University, Coimbatore, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 1, 2016; Accepted: November 6, 2016; Published: November 9, 2016
ABSTRACT
The Circular Restricted Three-Body Problem (CRTBP) with more massive primary as an oblate spheroid with its equatorial plane coincident with the plane of motion of the primaries is considered to generate the halo orbits around L1 and L2 for the seven satellites (Mimas, Enceladus, Tethys, Dione, Rhea, Titan and Iapetus) of Saturn in the frame work of CRTBP. It is found that the oblateness effect of Saturn on the halo orbits of the satellites closer to Saturn has significant effect compared to the satellites away from it. The halo orbits L1 and L2 are found to move towards Saturn with oblateness.
Keywords:
Circular Restricted Three-Body Problem, Lagrangian Points, Halo Orbits, Oblateness, Saturn

1. Introduction
Three-Body Problem formulated by Newton provided route to the analysis of closed form analytical solution. This solution remains elusive even today, as one has never been found for the three-body problem. Euler developed the restricted problem using a rotating frame in the 1770s and located collinear points. Along with Euler, Lagrange considered this form of the three-body problem and calculated the locations of equilateral points, often known as libration or Lagrange points. Jacobi studied the circular- restricted problem (CRTBP) and found that an integral of motion exists. Plummer [1] , using an approximate, second-order analytical solution to the differential equations in the circular restricted three-body problem, produced a family of two-dimensional periodic orbits near the collinear libration points. Farquhar in mid 1960s initiated an analytical investigation into a class of periodic three-dimensional trajectories around the collinear points known as halo orbits. These trajectories are associated with the collinear points, and are a special case of the more general libration point orbits frequently designated as Lissajous orbits. Kamel and Farquhar [2] developed analytical approximations for quasi-periodic solutions associated with L2, the Earth-Moon libration point on the far side of the Moon. Richardson and Cary [3] derived a third-order approximation for motion near the interior Sun-Earth liberation point in the restricted problem. Mission design utilizing the halo orbits become more challenging and several works had been established since then in this interesting area. Some of the important contributions are by Farquhar et al. [4] , Richardson [5] , Huber et al. [6] , Gomez et al. [7] [8] , Rausch [9] , Nakamiya et al. [10] , Koon et al. [11] and Nath & Ramanan [12] . Considering the motion in the vicinity of the collinear points in CRTBP, Breakwell and Brown [13] numerically extended the work of Farquhar and Kamel [2] to produce a family of periodic halo orbits. The discovery of a set of stable orbits in Breakwell and Brown’s halo family motivated a search for stable orbits in the families associated with all the three collinear points by Howell [14] [15] and Howell et al. [16] .
The subject of periodic solutions of the CRTBP has received enormous attention in the past few decades. Since the late twentieth century until today, enormous amount of research has enriched the study of CRTBP, but the influence of the various perturbing forces has not been studied in many of such interesting problems. The classical model does not account for some of the perturbing forces such as oblateness, solar radiation pressure, Poynting-Robertson drag effects and variation in the mass of the primaries. Some of significant works in RTBP with oblateness effects are done by Sharma and Subba Rao [17] [18] , Subba Rao and Sharma [19] - [21] and Sharma [22] - [25] by considering the more massive primary as an oblate spheroid with its equatorial plane co-incident with the plane of motion of the primaries. Danby [26] , Papadakis [27] , Kalantonis et al. [28] , Raheem et al. [29] , Stuchi et al. [30] discussed the restricted three-body problem with one or two bodies as oblate spheroids. The perturbing force due to the oblateness of Saturn is comparable with the perturbing force due to the gravitational attraction of the Sun in the Saturn-Satellites systems. The inclusion of oblateness effect has shown significant improvement in the theories of motion of certain satellites in the solar system [31] (Oberti and Vienne).
In the present study, we consider the restricted three-body problem by considering the more massive primary as an oblate spheroid with its equatorial plane coincident with the plane of motion (Sharma and Subba Rao [17] ). We utilize Newton’s method of differential correction (Mireles [32] ; Eapen and Sharma [33] ; Nishanth and Sharma [34] ) to compute the halo orbits numerically about the Lagrangian points L1 and L2 in seven of the Saturn-Satellites systems.
2. Equations of Motion
The equations of motion for the restricted three-body problem are considered with ,
, 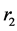 and
and 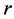 as the positions of three bodies with masses
as the positions of three bodies with masses 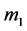 (more massive oblate spheroid-Saturn),
(more massive oblate spheroid-Saturn), 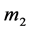 (Satellite of Saturn) and
(Satellite of Saturn) and 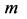 (spacecraft).
(spacecraft).
The origin of the co-ordinate system is the barycentre of the two primaries with the more massive primary lying to the left of the origin and the smaller primary to the right as shown in Figure 1. For scaling purpose, the distance between the two primaries is taken as unity, the sum of masses of the primaries 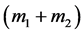 is assumed unity, and the gravitational constant is assumed to be unity. Then the mean motion of the primaries is
is assumed unity, and the gravitational constant is assumed to be unity. Then the mean motion of the primaries is
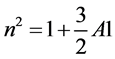 , where
, where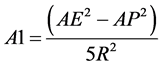 .
.
AE and AP are dimensional equatorial and polar radii of the more massive primary and R is the distance between the primaries.
The non-dimensional mass ratio 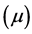 is defined as the ratio of the mass of the smaller primary to the sum of masses of the primaries i.e.
is defined as the ratio of the mass of the smaller primary to the sum of masses of the primaries i.e. .
.
The parameter  defines the position of the larger and smaller primaries as
defines the position of the larger and smaller primaries as 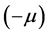 and
and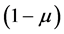 , respectively (Szebehely [35] ; Sharma [17] ; Bhatnagar and Chawla [36] ).
, respectively (Szebehely [35] ; Sharma [17] ; Bhatnagar and Chawla [36] ).
The three-dimensional equations of motion are:
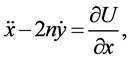 (1)
(1)
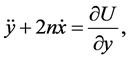 (2)
(2)
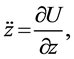 (3)
(3)
where 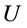 is the pseudo potential of the system and is given as
is the pseudo potential of the system and is given as
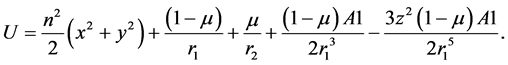
In the above expression 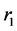
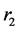
Figure 1. Diagram of the circular restricted three-body problem in normalized units
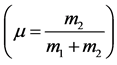
3. Liberation Points and Halo Orbits
From the equations of motion (1)-(3), it is apparent that an equilibrium solution exists relative to the rotating frame when the partial derivative of the pseudo potential function are all zero, i.e. 

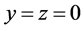
Richardson’s third-order approximation provides a deep qualitative insight. The approximate solution is sufficient for generating accurate motion near L1 and L2. Analytical approximation need to be combined with numerical techniques to generate a halo orbit accurate enough for mission design. In the present study to generate the halo orbits, we use analytical approximation as the first guess for the differential correction process, we have modified the third-order approximation of Thurman and Worfolk [37] by considering the more massive primary as an oblate spheroid with the help of Lindstedt-Poincaré method.
3.1. Analytical Approximation
For obtaining an analytical solution, following Tiwary and Kushvah [37] , the origin is transferred to the Lagrangian points L1 and L2 and the transformation is given by
The equations of motion can be written as
where
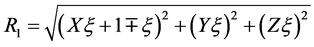
The upper sign in the above equations depicts the Lagrangian point L1 and the lower sign corresponds to L2.
The usage of Legendre polynomials can result in some computational advantages, when non-linear terms are considered. The distance between these Lagrangian points and the smaller primary is considered to be the normalized unit as in Koon et al. [11] [38] and [39] .
The non-linear terms are expanded by using the following formula as given by [11] :
where
The above formula is used for expanding the non-linear terms in the equations of motion. The equations of motion after substituting the values of the non-linear terms and carrying out some algebraic manipulations by defining a new variable cm after expanding up to m = 2 become
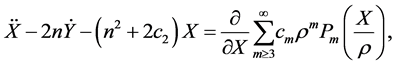


with
Neglecting the non-linear higher-order terms in Equations (5)-(7), we get
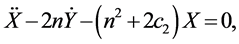
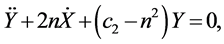
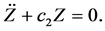
It is clear that the z-axis solution, obtained by putting X = Y = 0, does not depend upon X and Y and c2 > 0. Hence we can conclude that the motion in Z-direction is simple harmonic. The motion in XY-plane is coupled. A fourth degree polynomial is obtained which gives two real and two imaginary roots as eigenvalues:
The solution of the linearized Equations (7)-(9), as derived in [36] , is
where
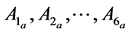
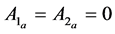
There is a necessity to introduce frequency and amplitude terms to perform the Lindstedt-Poincaré method. The solution of the linearized equations is again written in terms of amplitudes (Ax and Az) and phases (in-plane phase, ϕ and out-of-plane phase, ψ) and the frequencies (λ and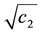

The amplitudes 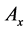
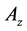
where l1 and l2 depend upon the roots of the characteristic equation of the linear equation. The correction term, 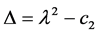
Hence, any halo orbit can be characterized by specifying a particular out-of-plane amplitude 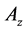
The phases ϕ and ψ are related as
When Ax is greater than certain value, the third-order solution bifurcates. This bifurcation is manifested through the phase-angle constraint. The solution branches are obtained according to the value of m. For m = 1, Az is positive and we have the northern halo (z > 0) and for m = 3, Az is negative and we have the southern halo (z < 0).
Lindstedt-Poincaré method involves successive adjustments of the frequencies to avoid secular terms and allows one to obtain approximate periodic solution. The equations of motion with non-linear terms up to third-order approximation as in Richardson and Thurman and Worfolk are
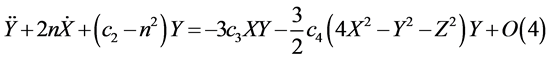
A new independent variable τ = ωt is introduced, where 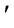
It is to be noted that the values of 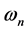
The coefficients 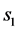
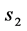

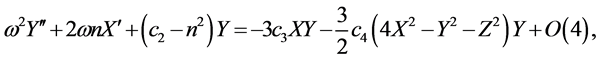
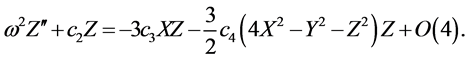
We continue the perturbation analysis by assuming the solutions of the form:
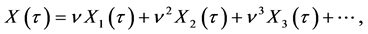
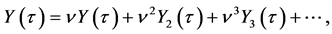
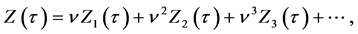
where 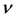
Substituting Equations (14)-(16) in Equations (11)-(13), and equating the coefficients of the same order of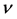
3.1.1. First-Order Equations
The first-order equations are obtained by taking the coefficients of the term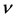
The periodic solution to the above equations is
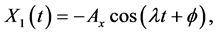


where k = k2.
3.1.2. Second-Order Equations
By collecting the terms of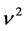
where
To remove the secular terms, we need to set the value ω1 = 0. The particular solution of the second-order equations are obtained with the help of Maxima software as
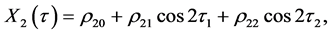
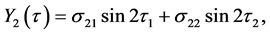
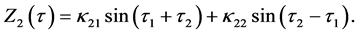
The coefficients are given in the Appendix.
3.1.3. Third-Order Equations
By collecting the terms of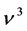
where
From the above equations, it is not possible to remove the secular terms by setting ω2 = 0. Hence, the phase relation is used here to remove the secular terms.
The solution of the third-order equation is obtained as
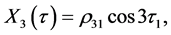

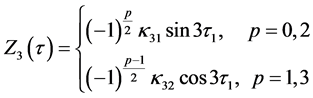
The coefficients are given in the Appendix. Thus, the third-order analytical solution is developed.
3.1.4. Final Approximation
The mapping, 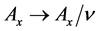
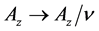
The coefficients are given in the Appendix.
3.2. Numerical Computation of Halo Orbits
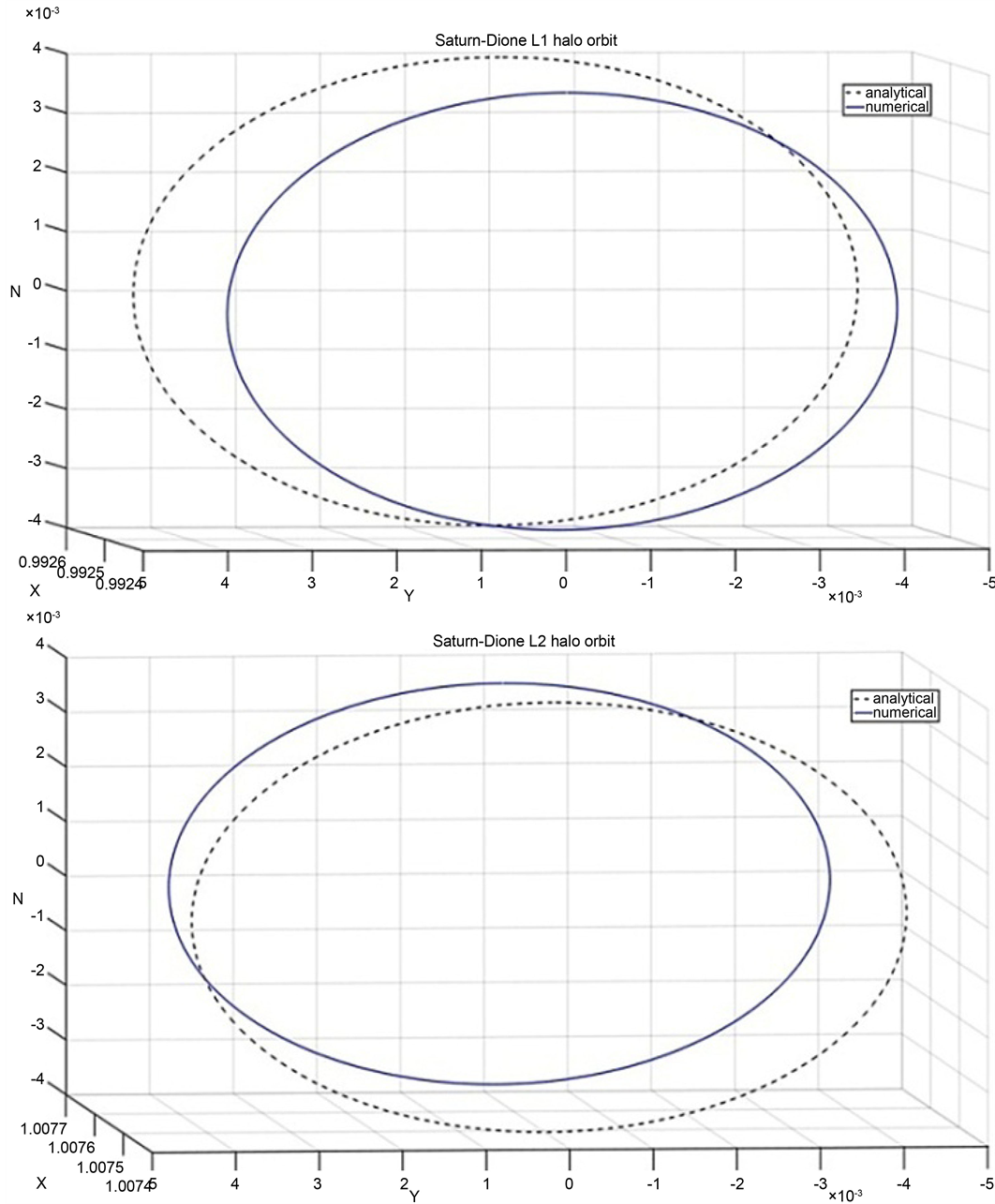
The method of differential correction is a powerful application of Newton’s method that employs the state transition matrix (STM) to solve various boundary value problems. Differential correction method is used to determine the initial conditions of the halo orbits from the initial guess [32] [34] [40] . Taking advantage of the fact that halo orbits are symmetric about xz-plane, the initial state vector takes the form
The equations of motion and state transition matrix are integrated numerically until the trajectory crosses the xz-plane again. The desired final condition is of the form
It is obtained by modifying the known parameters of the initial state vector. Then the orbit will be periodic with period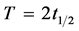
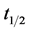
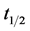
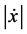
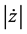
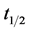
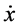
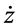
4. Halo Orbits in the Saturn-Satellites System
Saturn, the sixth planet from the Sun, is home to a vast array of intriguing and unique satellites. It is also the largest oblate body in the solar system. Hence, studying the halo orbits about the moons of Saturn is interesting to observe the oblateness effect on the periodic orbits about the collinear points of the Saturn-Satellite systems. Christian Huygens discovered Titan, the first known moon of Saturn in 1655. Jean-Dominique
Figure 2. Numerical and analytical solutions for Saturn-Mimas system.
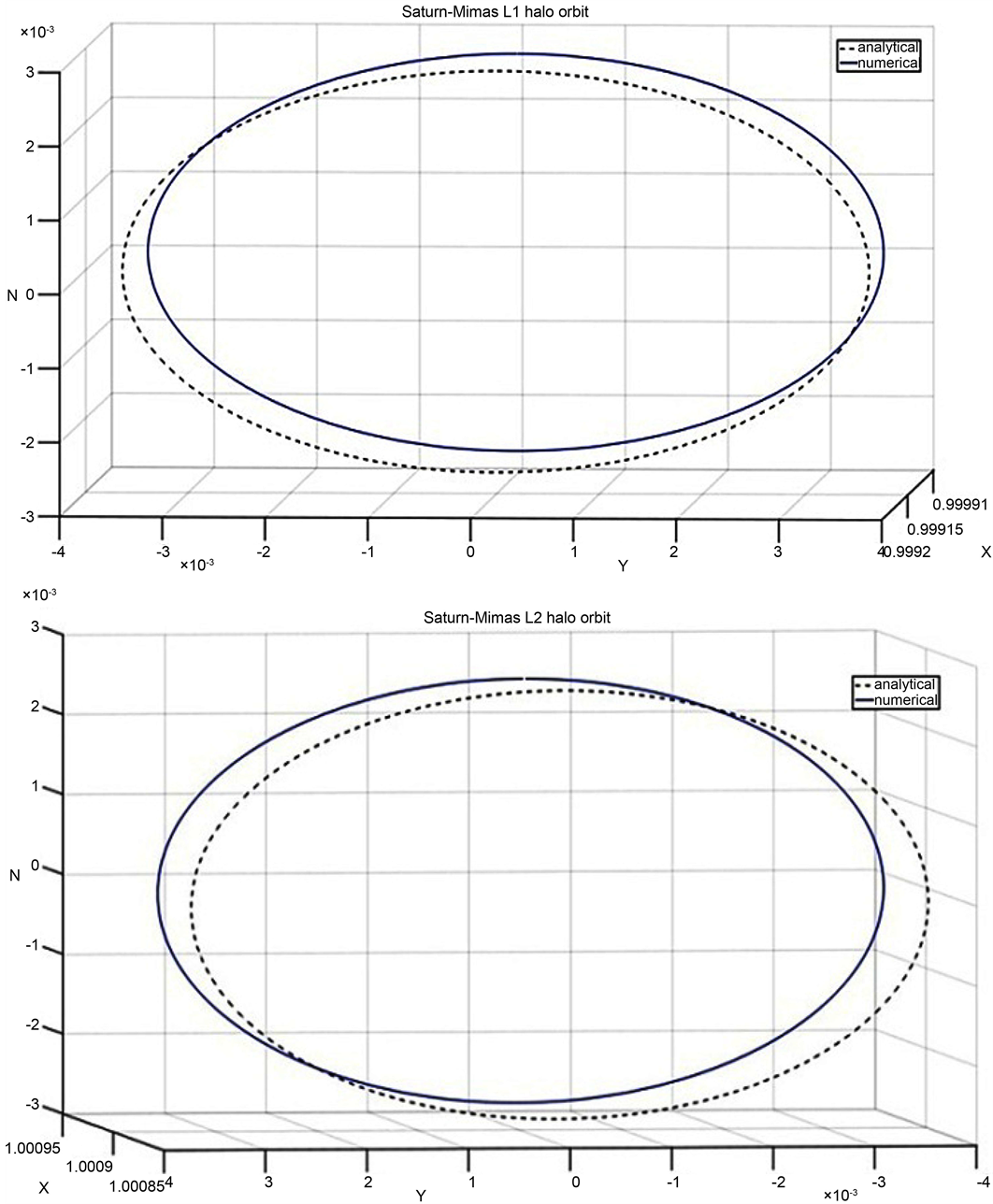
Figure 3. Numerical and analytical solutions for Saturn-Enceladus system.
Figure 4. Numerical and analytical solutions for Saturn-Tethys system.
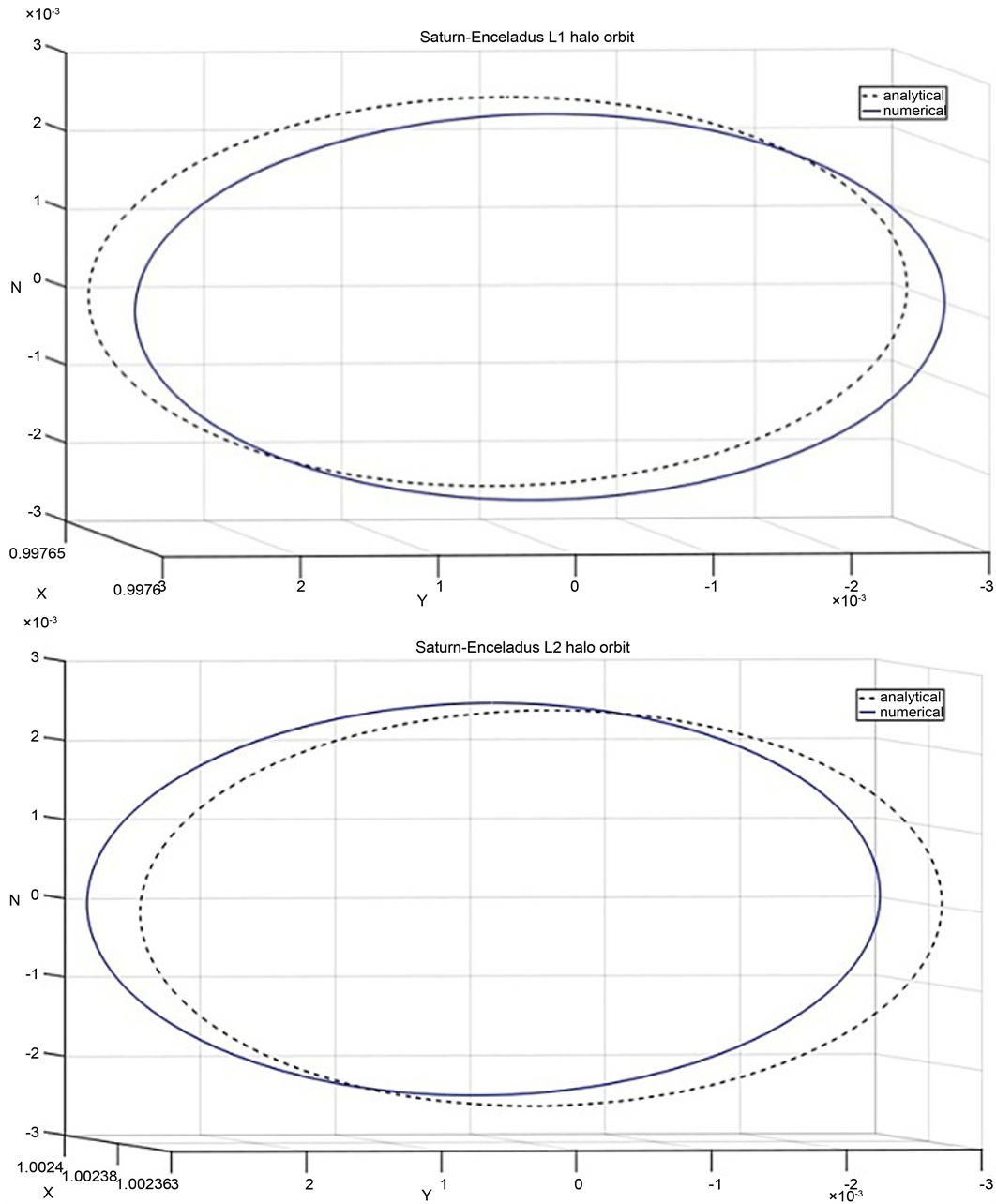
Figure 5. Numerical and analytical solutions for Saturn-Dione system.
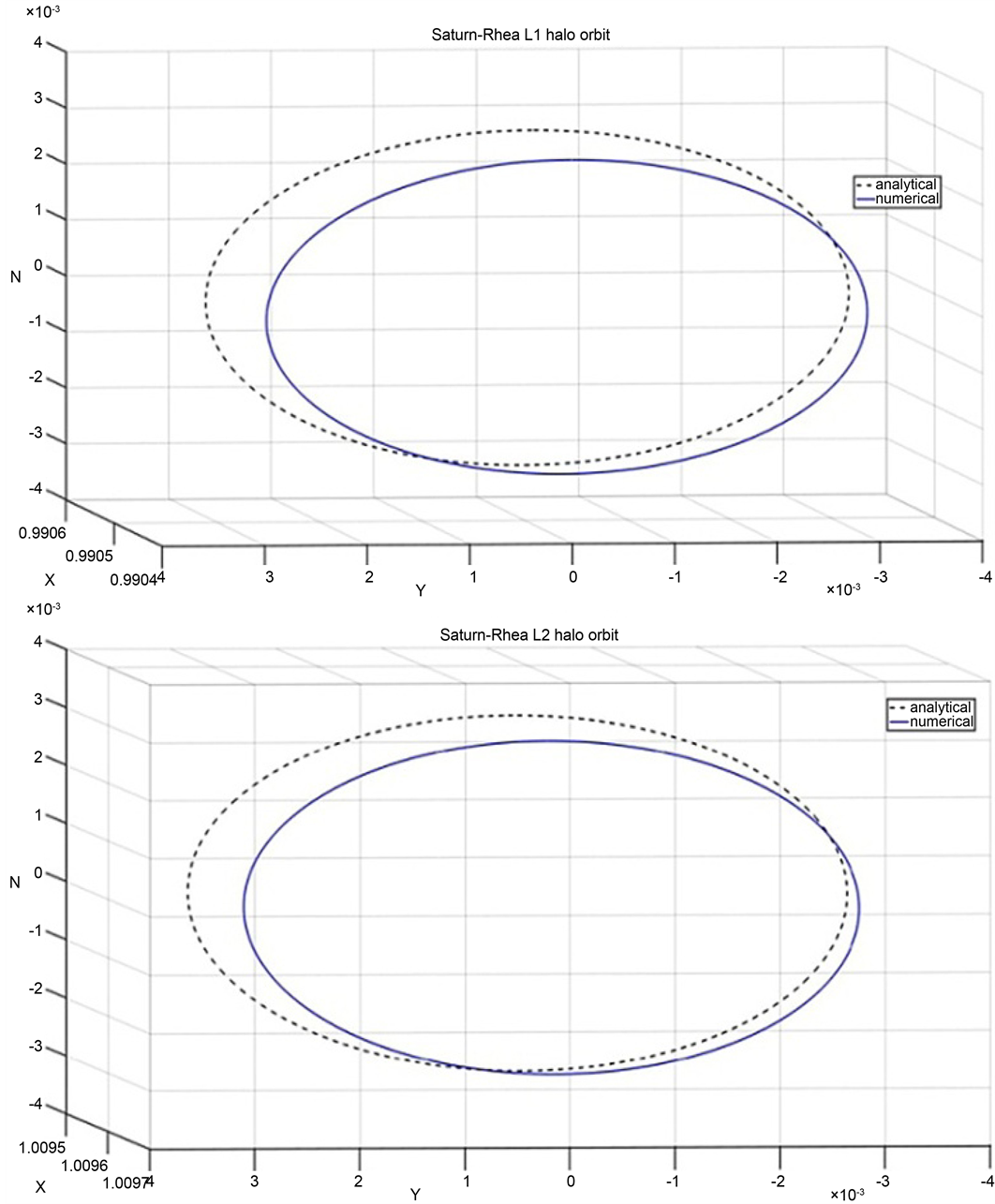
Figure 6. Numerical and analytical solutions for Saturn-Rhea system.
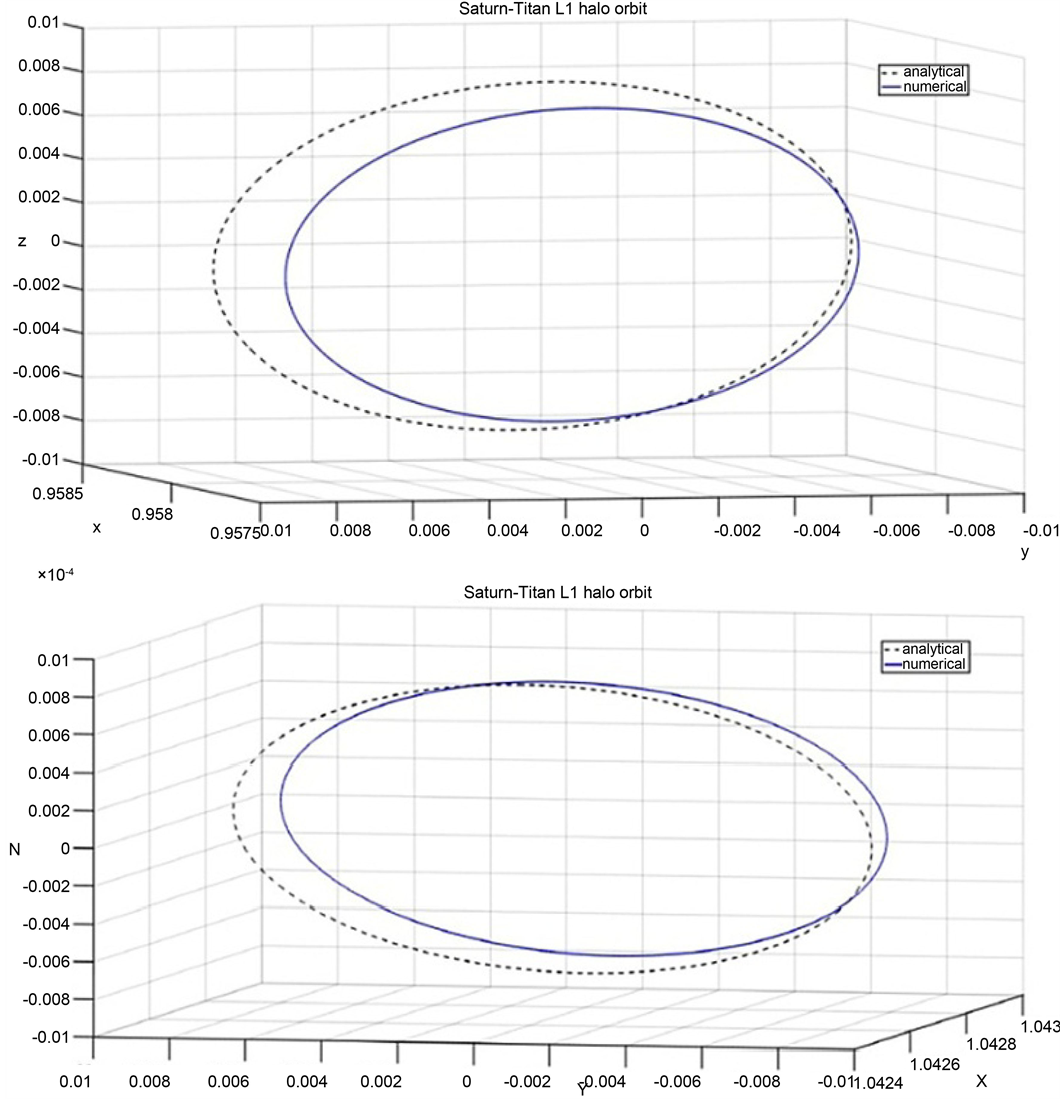
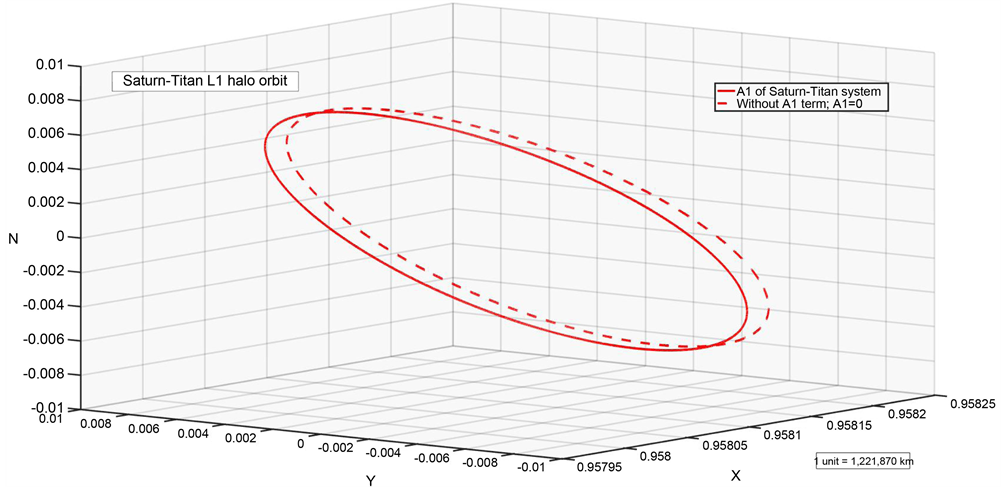
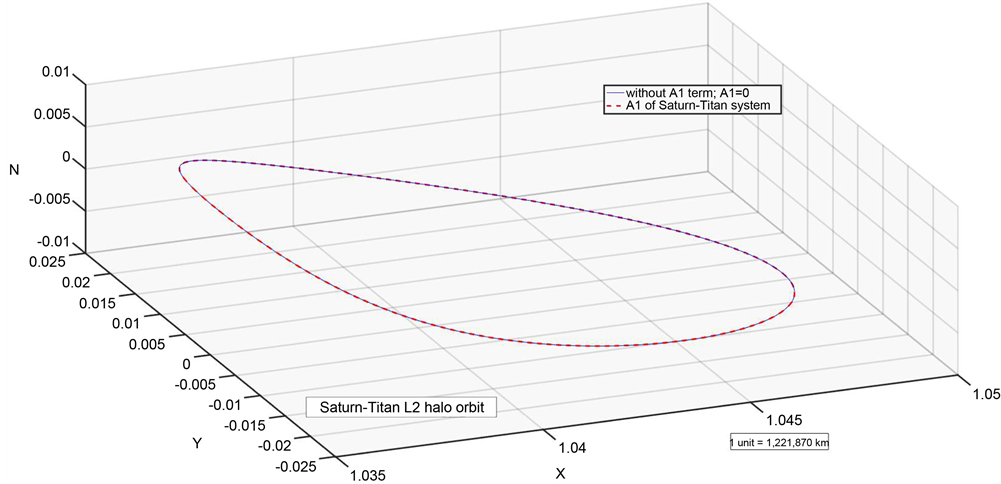
Figure 7. Numerical and analytical solutions for Saturn-Titan system.
Cassini made the next four discoveries: Iapetus (1671), Rhea (1672), Dione (1684), and Tethys (1684). Mimas and Enceladus were both discovered by William Herschel in 1789. We have used these known moons of Saturn for our study. The mass parameter μ and the oblateness coefficient A1 of the systems under study are presented in Table 1 [17] .
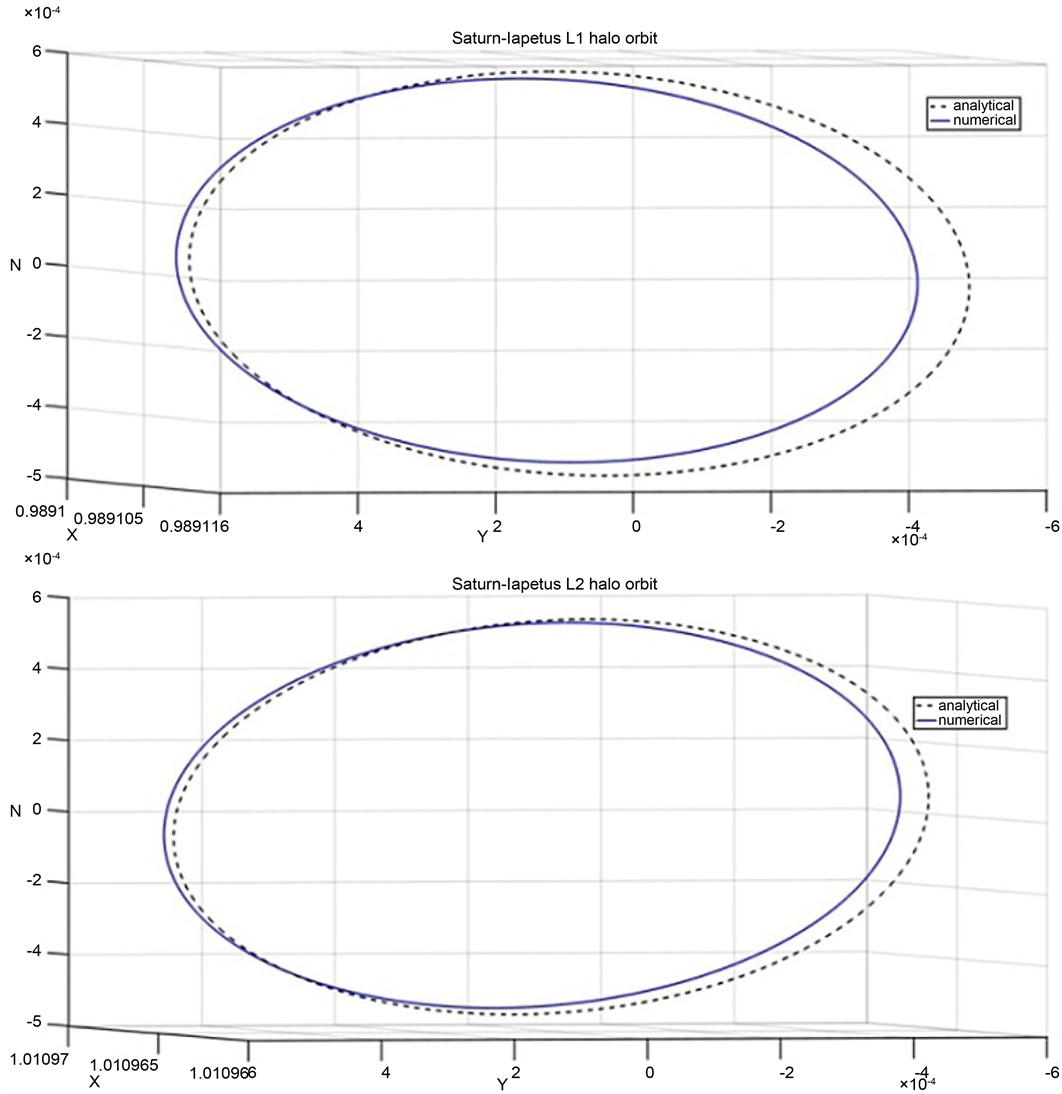
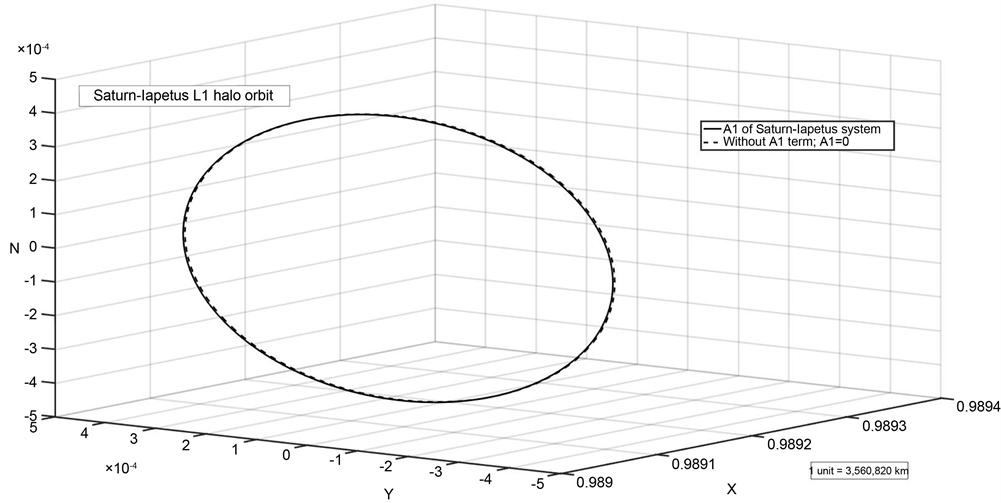
Figure 8. Numerical and analytical solutions for Saturn-Iapetus system.
4.1. Saturn-Mimas
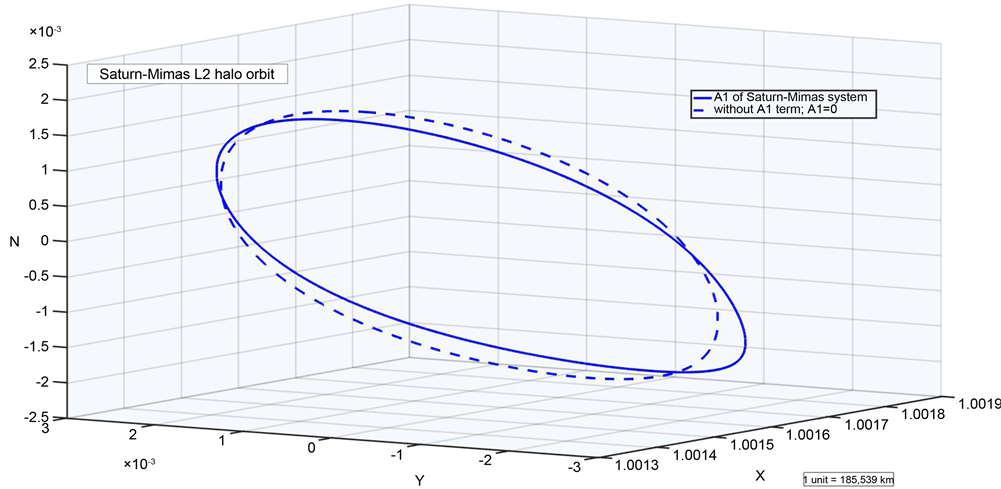
Mimas is the closest moon to Saturn which is considerably larger than other moons closer to Saturn. Mimas has an enormous crater on one side, the result of an impact that nearly split the moon apart. We have computed the initial guesses for the differential correction process provided in Table 2. The initial guess for the halo orbit computation about L1 and L2 of Saturn-Mimas system is subjected to differential correction process and then the equations of motion are numerically integrated with Adams-Bashforth- Moulton multistep method with relative tolerance of 2.5e−10 and absolute tolerance of 1.0e−14. Figure 9 and Figure 10 provide the variation of Saturn-Mimas L1 and L2 halo orbits with and without oblateness effect. We observe that the initial conditions change for different values of A1 and hence the orbits about the collinear points L1 and L2 shift. It is observed that the effect of Saturn’s oblateness on the halo orbits is significant
Table 1. Systems and their parameters.
Table 2. Initial conditions for Saturn-Mimas system.
Figure 9. Saturn-Mimas L1 halo orbit with and without oblateness.
and the L1 halo orbit shifts towards Saturn by 260 km and L2 halo orbit shifts by 11.6 km. We also find that the non-dimensional time period of the halo orbits increases at L1 and decreases at L2 of the Saturn-Mimas system.
4.2. Saturn-Enceladus
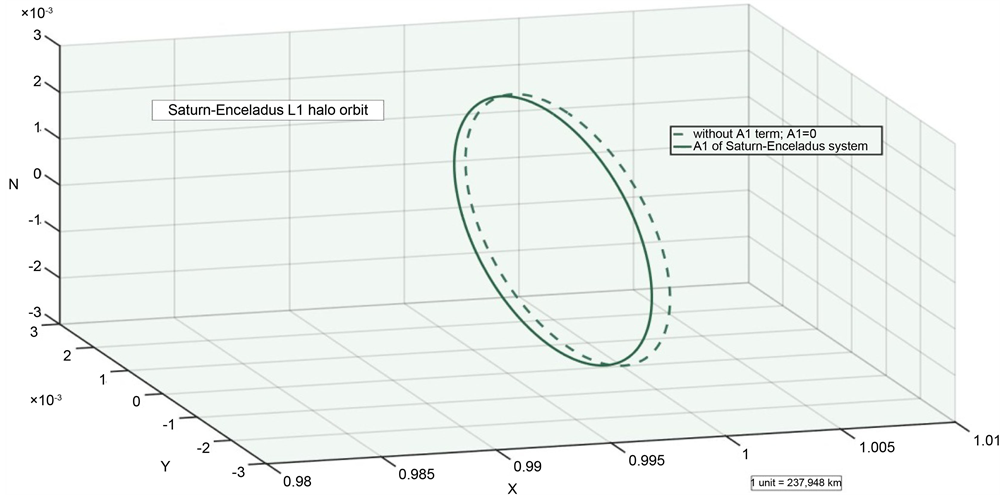
Enceladus is the second closest moon next to Mimas at a distance of 237,948 km from Saturn. It displays evidence of active ice volcanism. Cassini observed warm fractures where evaporating ice evidently escapes and forms a huge cloud of water vapour over the South Pole. Similar to Saturn-Mimas system, we compute the halo orbits about the L1 and L2 of Saturn-Enceladus system with the initial guesses provided in Table 3 and the parameters taken from Table 1. We refine these conditions with differential correction method and compute halo orbits numerically. The oblateness effect on this system is lesser than on Saturn-Mimas system. Figure 11 and Figure 12 provide the L1 and L2 halo orbits with and without oblateness for Saturn-Enceladus system.
We observe that the halo orbits about L1 and L2 shift towards Saturn with oblateness by 153 km and 25 km, respectively. Similar to Saturn-Mimas system, the non-dimen- sional time period of the halo orbit increases at L1 and decreases at L2.
Figure 10. Saturn-Mimas L2 halo orbit with and without oblateness.
Table 3. Initial conditions for Saturn-Enceladus system.
Figure 11. Saturn-Enceladus L1 halo orbit with and without oblateness.
Figure 12. Saturn-Enceladus L2 halo orbit with and without oblateness.
4.3. Saturn-Tethys
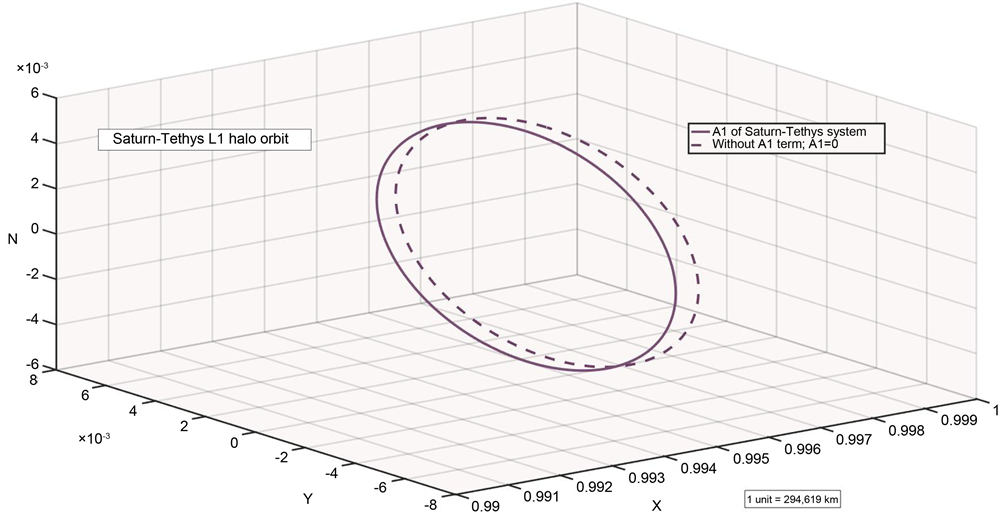
Tethys is the third closest and interesting satellite of Saturn at a distance of 294,619 km. Tethys has a huge rift zone called Ithaca Chasma that runs nearly three-quarters of the way around the moon. Telesto and Calypso are the two moons occupying the two Lagrangian points of Saturn-Tethys system. With the help of the initial guess, we compute the halo orbits about L1 and L2 of Saturn-Tethys system using the parameters of Table 1 and Table 4. Figure 13 and Figure 14 illustrate the L1 and L2 halo orbits. We observe that, the initial conditions change for different values of A1 and the halo orbits shift towards Saturn by 101 km at L1 and 3 km at L2.
4.4. Saturn-Dione
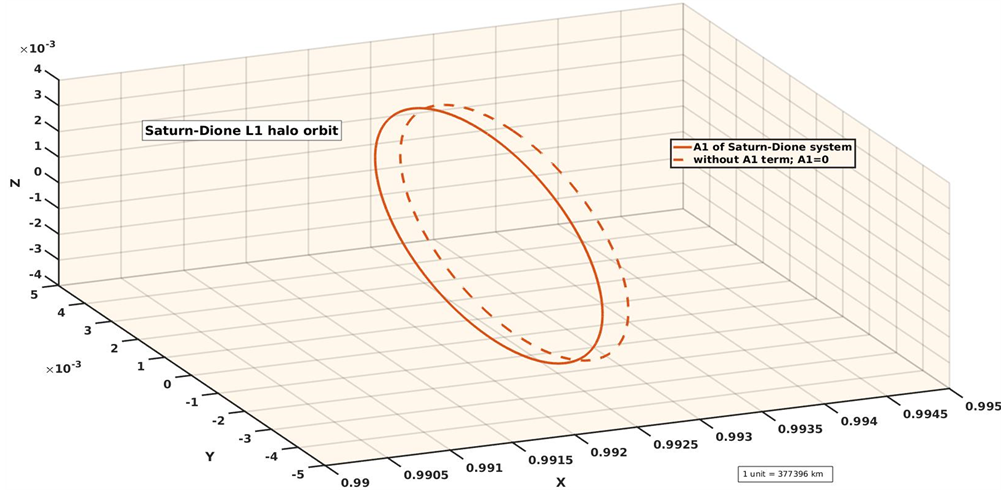
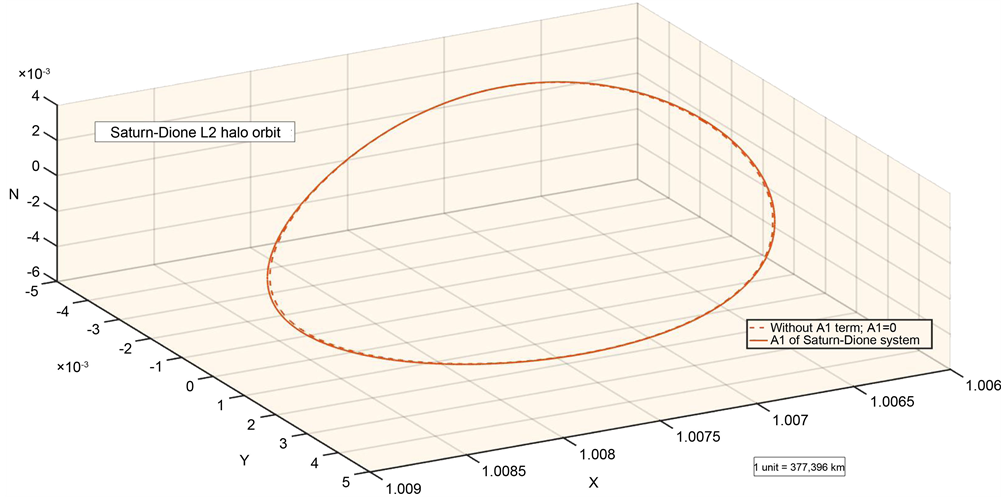
Dione is the fourth closest moon of Saturn with considerable higher mass than Tethys, and is 377,396 km from Saturn. Similar to Tethys, Helene and Poly deuces are the two other moons occupy the corresponding Lagrangian points of Dione in Saturn-Dione system. Using Table 1 and Table 5, we compute the L1 and L2 halo orbits of Saturn-Dione system. These are shown in Figure 15 and Figure 16, respectively. The L1 halo orbit moves towards Saturn by 77.15 km and L2 halo orbit moves towards it by 0.48 km with oblateness.
4.5. Saturn-Rhea
Rhea is the moon of Saturn orbiting about 527,108 km from Saturn. It experiences the oblateness effect of Saturn very less compared to the previous moons. Using Table 1
Table 4. Initial conditions for Saturn-Tethys system.
Figure 13. Saturn-Tethys L1 halo orbit with and without oblateness.
Figure 14. Saturn-Tethys L2 halo orbit with and without oblateness.
Figure 15. Saturn-Dione L1 halo orbit with and without oblateness.
Table 5. Initial conditions for Saturn-Dione system.
and Table 6, the L1 and L2 halo orbits of Saturn-Rhea system are computed and are plotted in Figure 17 and Figure 18 with and without oblateness. L1 halo orbit moves towards Saturn by 50.3 km and L2 halo orbit moves towards it by 0.3 km.
4.6. Saturn-Titan
Titan is the solar system’s second-largest moon with 5150 km diameter after Ganymede (5362 km) of Jupiter. Titan hides its surface beneath a thick, nitrogen-rich atmosphere. Cassini’s instruments have revealed that Titan possesses many parallels to Earth-clouds, dunes, mountains, lakes, and rivers. Titan’s atmosphere is approximately 95 percent nitrogen with traces of methane. While Earth’s atmosphere extends about 60 km into space, Titan’s extends nearly by 600 km (10 times that of Earth’s atmosphere) into space. Effect of oblateness of Saturn on Titan in the frame work of restricted three-body problem was previously studied by Beevi and Sharma [41] [42] . Here we compute L1 and L2 halo orbits about Saturn-Titan system under the effects of Saturn’s oblateness. Table 1 and Table 7 provide the initial conditions for numerical computation of these orbits. It is noticed that the effect of Saturn’s oblateness on the halo orbit is quite less.
Figure 16. Saturn-Dione L2 halo orbit with and without oblateness.
Table 6. Initial conditions for Saturn-Rhea system.
Figure 17. Saturn-Rhea L1 halo orbit with and without oblateness.
Figure 18. Saturn-Rhea L2 halo orbit with and without oblateness.
Table 7. Initial conditions for Saturn-Titan system.
Oblateness attracts L1 halo orbit towards Saturn by 2.88 km and L2 halo orbit by 0.1 km. Figure 19 and Figure 20 show Saturn-Titan L1 and L2 halo orbits. As is expected, the effect of oblateness on the halo orbits decreases as the distance between the satellites of Saturn and the planet (Saturn) increases.
4.7. Saturn-Iapetus
Iapetus has one side as bright as snow and other side as dark as black velvet, with a huge
Figure 19. Saturn-Titan L1 halo orbit with and without oblateness.
Figure 20. Saturn-Titan L2 halo orbit with and without oblateness.
ridge running around most of its dark-side equator. Iapetus is 3,560,820 km from Saturn and is smaller than Titan, Rhea and larger than Mimas, Enceladus. Initial conditions for computation of L1 and L2 halo orbits of Saturn-Iapetus system are given in Table 8. Figure 21 and Figure 22 show L1 and L2 halo orbits for this system. The effect of oblateness on the halo orbits of Saturn-Iapetus system is found to be negligible.
5. Results and Conclusion
Halo orbits in the vicinity of L1 and L2 collinear points in Saturn-Satellites systems in the frame work of circular restricted three-body problem with more massive primary Saturn as an oblate spheroid with its equatorial plane coincident with the plane of motion of the primaries are considered. The halo orbits with oblateness effect of Saturn for seven largest satellites of Saturn are computed through the differential correction method of Mireles [32] . It is found that oblateness effect on halo orbits of the satellites closer to Saturn has significant effect compared to the satellites away from it. The halo orbits L1 and L2 are found to move towards Saturn with oblateness effect and the results are tabulated in Table 9.
Table 8. Initial conditions for Saturn-Iapetus system.
Figure 21. Saturn-Iapetus L1 halo orbit with and without oblateness.
Figure 22. Saturn-Iapetus L2 halo orbit with and without oblateness.
Table 9. Variation in location and time period of halo orbit with oblateness effect.
Acknowledgements
Cite this paper
Pushparaj, N. and Sharma, R.K. (2016) Oblateness Effect of Saturn on Halo Orbits of L1 and L2 in Saturn-Satellites Restricted Three-Body Problem. International Journal of Astronomy and Astrophysics, 6, 347-377. http://dx.doi.org/10.4236/ijaa.2016.64029
References
- 1. Plummer, H. (1903) On Oscillating Satellites—1. Monthly Notices of the Royal Astronomical Society, 63, 436-443.
http://dx.doi.org/10.1093/mnras/63.8.436 - 2. Farquhar, R.W. and Kamel, A.A. (1973) Quasi-Periodic Orbits about the Translunar Libration Point. Celestial Mechanics, 7, 458-473.
http://dx.doi.org/10.1007/BF01227511 - 3. Richardson, D.L. and Cary, N.D. (1975) A Uniformly Valid Solution for Motion about the InteriorLibration Point of the Perturbed Elliptic-Restricted Problem. AIAA/AAS Astrodynamics Specialists Conference, Nassau, 28-30 July 1975, AAS PAPER 75-021.
- 4. Farquhar, R.W., Muhonen, D.P. and Richardson, D.L. (1977) Mission Design for a Halo Orbiter of the Earth. Journal of Spacecraft and Rockets, 14, 170-177.
- 5. Richardson, D.L. (1980) Analytic Construction of Periodic Orbits about the Collinear Points. Celestial Mechanics, 22, 241-253.
http://dx.doi.org/10.1007/BF01229511 - 6. Huber, M., Bonnet, R., Dale, D., Arduini, M., Fröhlich, C., Domingo, V. and Whitcomb, G. (1996) The History of the SOHO Mission. ESA Bulletin, 86, 25-35.
- 7. Gómez, G., Jorba, A., Simó, C. and Masdemont, J. (2001) Dynamics and Mission Design near Libration Points. In: Vol. III: Advanced Method for Collinear Points, World Scientific, New Jersey, 204 p.
- 8. Gómez, G., Llibre, J., Marti ′nez, R. and Simó, C. (2001) Dynamics and Mission Design near Libration Points. In: Vol. I: Fundamentals: The Case of Collinear Libration Points, World Scientific, New Jersey, 464 p.
- 9. Rausch, R.R. (2005) Earth to Halo Orbits Transfer Trajectory. Purdue University.
https://engineering.purdue.edu/people/kathleen.howell.1/.../2005_Rausch.pdf - 10. Nakamiya, M., Scheeres, D.J., Yamakawa, H. and Yoshikawa, M. (2008) Analysis of Capture Trajectories into Periodic Orbits about Liberation Points. Journal of Guidance, Control and Dynamics, 31, 5.
http://dx.doi.org/10.2514/1.33796 - 11. Koon, W.S., Lo, M.W., Marsden, J.E. and Ross, S.D. (2011) Dynamical Systems: The Three Body Problem and Space Mission Design. Springer, New York, 335 p.
http://www.cds.caltech.edu/~koon/research/3body/Equadiff_mission_2-8-00.pdf - 12. Nath, P. and Ramanan, R.V. (2016) Precise Halo Orbit Design and Optimal Transfer to Halo Orbits from Earth Using Differential Evolution. Advances in Space Research, 57, 202-217.
http://dx.doi.org/10.1016/j.asr.2015.10.033 - 13. Breakwell, J.V. and Brown, J.V. (1979) The Halo Family of 3-Dimensional Periodic Orbits in the Earth-Moon Restricted Three Body Problem. Celestial Mechanics, 20, 389-404.
http://dx.doi.org/10.1007/BF01230405 - 14. Howell, K.C. (1983) Three-Dimensional, Periodic “Halo” Orbits in the Restricted Three-Body Problem. Ph.D. Dissertation, Department of Aeronautics and Astronautics, Stanford University, Stanford, California.
- 15. Howell, K.C. (1984) Three-Dimensional, Periodic “Halo” Orbits. Celestial Mechanics, 32, 53-71.
http://dx.doi.org/10.1007/BF01358403 - 16. Howell, K.C., Barden, B.T. and Lo, M.W. (1997) Application of Dynamical Systems Theory to Trajectory Design for a Libration Point Mission. Journal of the Astronautical Sciences, 45, 161-178.
- 17. Sharma, R.K. and Subba Rao, P.V. (1976) Stationary Solutions and Their Characteristic Exponents in the Restricted Three-Body Problem When the More Massive Primary Is an Oblate Spheroid. Celestial Mechanics, 13, 137-149.
http://dx.doi.org/10.1007/BF01232721 - 18. Sharma, R.K. and Subba Rao, P.V. (1986) On Finite Periodic Orbits around the Equilibrium Solutions of the Planar Restricted Three-Body Problem. In: Bhatnagar, K.B., Ed., Space Dynamics and Celestial Mechanics, D. Reidel Publishing Company, Dordrecht, 71-85.
http://dx.doi.org/10.1007/978-94-009-4732-0_8 - 19. Subba Rao, P.V. and Sharma, R.K. (1975) A Note on the Stability of the Triangular Points of Equilibrium in the Restricted Three-Body Problem. Astronomy & Astrophysics, 43, 381-381.
- 20. Subba Rao, P.V. and Sharma, R.K. (1988) Oblateness Effect on Finite Periodic Orbits at L4. 39th Congress of the International Astronautical Federation (IAF-88-300), Bangalore, India, 8-15 October, 6.
- 21. Subba Rao, P.V. and Sharma, R.K. (1997) Effect of Oblateness on the Non-Linear Stability of L4 in the Restricted Three-Body Problem. Celestial Mechanics and Dynamical Astronomy, 65, 291-312.
http://dx.doi.org/10.1007/BF00053510 - 22. Sharma, R.K. (1981) Periodic Orbits of Second Kind in the Restricted Three-Body Problem When the More Massive Primary Is an Oblate Spheroid. Astrophysics and Space Sciences, 76, 255-258.
http://dx.doi.org/10.1007/BF00651258 - 23. Sharma, R.K. (1987) The Linear Stability of Libration Points of the Photogravitational Restricted Three-Body Problem When the Smaller Primary Is an Oblate Spheroid. Astrophysics and Space Science, 135, 271-281.
http://dx.doi.org/10.1007/BF00641562 - 24. Sharma, R.K. (1989) The Periodic Orbits of the Second Kind in Terms of Giacaglia’s Variables with Oblateness. Earth, Moon, and Planets, 45, 213-218.
http://dx.doi.org/10.1007/BF00057744 - 25. Sharma, R.K. (1990) Periodic Orbits of Third Kind in the Restricted Three-Body Problem with Oblateness. Astrophysics and Space Science, 166, 211-218.
http://dx.doi.org/10.1007/BF01094894 - 26. Danby, J.M.A. (1965) Inclusion of Extra Forces in the Problem of Three Bodies. Astronomical Journal, 70, 181-189.
http://dx.doi.org/10.1086/109712 - 27. Papadakis, K.E. (2004) The Planar Hill Problem with Oblate Primary. Astrophysics and Space Science, 293, 271-289.
http://dx.doi.org/10.1023/B:ASTR.0000044300.66267.1d - 28. Kalantonis, V.S., Douskos, C.N. and Perdios, E.A. (2006) Numerical Determination of Homoclinic and Heteroclinic Orbits as Collinear Equilibria in the Restricted Three-Body Problem with Oblateness. Celestial Mechanics and Dynamical Astronomy, 94, 135-153.
http://dx.doi.org/10.1007/s10569-005-4441-x - 29. Raheem, A., et al. (2006) Combined Effects of Perturbations, Radiation, and Oblateness on the Stability of Equilibrium Points in the Restricted Three-Body Problem. Astronomical Journal, 131, 1880-1885. http://dx.doi.org/10.1086/499300
- 30. Stuchi, T.J., et al. (2008) Dynamics of a Spacecraft and Normalization around Lagrangian Points in the Neptune-Triton system. Advances in Space Research, 42, 1715-1722.
http://dx.doi.org/10.1016/j.asr.2007.04.007 - 31. Oberti, P. and Vienne, A. (2003) An Upgraded Theory for Helene, Telesto, and Calypso. Astronomy and Astrophysics, 397, 353-359.
http://dx.doi.org/10.1051/0004-6361:20021518 - 32. Mireles, J.D. (2006) The State Transition Matrix and Method of Differential Corrections. Rutgers University.
http://cosweb1.fau.edu/~jmirelesjames/celestHw2Notes.pdf - 33. Eapen, R.T. and Sharma, R.K. (2014) A Study of Halo Orbits at the Sun-Mars L1 Lagrangian Point in the Photo-Gravitational Restricted Three-Body Problem. Astrophysics and Space Science, 353, 65-71. http://dx.doi.org/10.1007/s10509-014-2012-x
- 34. Nishanth, P. and Sharma, R.K. (2016) Halo Orbits at Sun-Mars L1, L2 in the Photogravitational Restricted Three-Body Problem with Oblateness. Advances in Astrophysics, 3, 18 p.
- 35. Szebehely, V. (1967) Theory of Orbits. The Restricted Problem of Three Bodies. Academic press, New York.
- 36. Bhatnagar, K.B. and Chawla, J.M. (1979) A Study of the Lagrangian Points in the Photogravitational Restricted Three-Body Problem. Indian Journal of Pure and Applied Mathematics, 10, 1443-1451.
http://www.insa.nic.in/writereaddata/UpLoadedFiles/IJPAM/20005a66_1443.pdf - 37. Thurman, R. and Worfolk, P.A. (1996) The Geometry of Halo Orbits in the Circular Restricted Three-Body Problem. Technical report, University of Minnesota, Minneapolis.
- 38. Tiwary, R.D. and Kushvah, B.S. (2015) Computation of Halo Orbits in the Photogravitational Sun-Earth System with Oblateness. Astrophysics and Space Science, 357, 1-16.
http://dx.doi.org/10.1007/s10509-015-2243-5 - 39. Prithiviraj, C. and Sharma, R.K. (2016) Halo Orbits around Sun-Earth L1 in Photogravitational Restricted Three-Body Problem with Oblateness of Smaller Primary. International Journal of Astronomy and Astrophysics, 6, 293-311.
http://dx.doi.org/10.4236/ijaa.2016.63025 - 40. McInnes, A. (2009) An Introduction to Liberation Point Orbits.
http://coweb.elec.canterbury.ac.nz/cda/uploads/mcinnes-intro_to_libration_point_orbits.pdf - 41. Beevi, A.S. and Sharma, R.K. (2011) Analysis of Periodic Orbits in the Saturn-Titan System Using the Method of Poincare Section Surfaces. Astrophysics and Space Science, 333, 37-48.
http://dx.doi.org/10.1007/s10509-011-0630-0 - 42. Beevi, A.S. and Sharma, R.K. (2012) Oblateness Effect of Saturn on Periodic Orbits in the Saturn-Titan Restricted Three-Body Problem. Astrophysics and Space Science, 340, 245-261.
http://dx.doi.org/10.1007/s10509-012-1052-3
Appendix
Coefficients for the second and third-order equations and solution:
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ijaa@scirp.org