International Journal of Astronomy and Astrophysics
Vol.05 No.04(2015), Article ID:60226,4 pages
10.4236/ijaa.2015.54027
If Quantum “Wave” of the Universe Then Quantum “Particle” of the Universe: A Resolution of the Dark Energy Question and the Black Hole Information Paradox
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 September 2015; accepted 9 October 2015; published 12 October 2015
ABSTRACT
We start from a minimal number of generally accepted premises, in particular Hartle-Hawking quantum wave of the universe and von Neumann-Connes’ pointless and self referential spacetime geometry. We then proceed from there to show, using Dvoretzky’s theorem of measure concentra- tion, that the total energy of the universe is divided into two parts, an ordinary energy very small part which we can measure while most of the energy is concentrated as the second part at the boundary of the holographic boundary which we cannot measure in a direct way. Finally the results are shown to imply a resolution of the black hole information paradox without violating the fundamental laws of physics. In this way the main thrust of the two opposing arguments and views, namely that of Hawking on the one side and Susskind as well as tHooft on the other side, is brought to a consistent and compatible coherent unit.
Keywords:
Dvoretzky Theory, Wave-Particle Duality, Von Neumann Pointless and Self Referential Geometry, Cantorian Spacetime, Hartle-Hawking Quantum Wave of the Universe, Dark Energy, Black Hole Information Paradox, Connes Noncommutative Geometry

1. Introduction
Within the framework of Einstein’s general relativity and the work of Hawking, Hartle, Penrose, Wheeler, Susskind and tHooft to mention only a few [1] - [20] , the present work is mainly concerned with the problem of dark energy [8] [12] [15] and what turned out to be related to it, namely the famous information paradox of black holes [14] - [19] .
We start from Hartle-Hawking quantum wave of the universe [1] - [5] . Using the wave-particle duality we reason that such a wave implies, by this well known duality, the existence of a corresponding quantum particle of the universe. Assuming the embedding spacetime of particle and wave to be akin to that of von Neumann-Con- nes’ pointless geometrical-topological quasi manifold [9] [11] , then it is a surprisingly simple task to calculate the entire energy density of the universe which is then shown by virtue of the celebrated theorem of Dvoretzky to split into two parts [12] [15] [16] . The first part is a measurable ordinary energy of about 4% to 4.5% of the total energy density and the second part is dark energy of about 95.5% to 96% of the total, which manifests its existence indirectly but cannot be measured directly [15] [16] . Noting the relation between energy and information via entropy we carry the aforementioned results over to the black hole information paradox and to our own great surprise resolves it without violating any fundamental laws of relativity or quantum theory [17] - [20] .
2. If Quantum Wave Then a Colossal Quantum Particle as the Quantum Universe
We emphasize once more what we said earlier on, namely that there is a definite quantum wave-particle duality in quantum physics, but this by no means implies that there can be wave without particle or vice versa [1] - [7] . The duality says only that we can observe the one or the other and nothing more. This is in fact the most important result of our previous quantum set foundation of orthodox or historical quantum mechanics, namely that the quantum wave is simply the cobordism of the quantum particle. More accurately since the quantum pre-particle is the zero set of von Neumann-Connes’ dimensional function [9] [15]
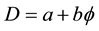 (1)
(1)
where 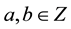 and
and 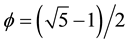 then it follows that the empty set is the cobordism of the zero set [15] . In more intuitive mundane terminology, the particle is the zero set with
then it follows that the empty set is the cobordism of the zero set [15] . In more intuitive mundane terminology, the particle is the zero set with  and its surface is the empty set with
and its surface is the empty set with . Here zero and
. Here zero and 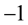 are Menger-Urysohn inductive topological dimensions and
are Menger-Urysohn inductive topological dimensions and 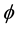 and
and 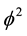
are the corresponding Hausdorff dimensions [21] . Now it is Hartle and Hawking who show that the Wheeler-de Witt equation [1] - [5] which is in essence a Schrödinger equation for the entire universe [1] can be solved to yield a wave function for the universe and consequently by the same fundamental duality, there must be a corresponding quantum particle also for the entire universe or we would not be here writing papers about dark energy and black hole information paradox [17] - [19] . That is why we gave this section the title we gave it and now we can proceed without further ado to the energy subdivisions [15] .
3. Dvoretzky’s Measure Concentration Theorem Applied to Cosmology of Dark Energy
In sufficiently high dimensional spaces, in particular a convex Banach space, Dvoretzky’s theorem [12] states that the volume of a sphere will be concentrated at the surface [12] . More accurately the theorem implies that 96% of the volume would be at the surface while in the so called “false” bulk we will have only 4% [22] [23] . For our quantum particle of the universe surrounded by its quantum wave of the universe, the set up can be envisaged as embedded in an at least five dimensional spacetime akin to that of Klein-Kaluza unification theory [12] . Consequently from the 100 percent energy density we will have 96% concentrated on the surface, i.e. in the quantum wave of the universe where 4% are inside the “particle” which constitutes the quantum particle of the entire universe [1] [12] . This division and the corresponding energy densities agree in every respect with the essential measurements and observations of COBE, WMAP, Hubble and Planck [8] [12] [16] . In the next section we see how to make this estimate almost exact.
4. The Ordinary Energy of the Quantum Particle and the Dark Energy of the Quantum Wave
Let us reformulate our basic model of a zero set 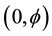 pre-particle [12] [15] [16] surrounded by its cobordism, i.e. its empty set
pre-particle [12] [15] [16] surrounded by its cobordism, i.e. its empty set 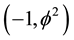 pre-wave surface, this time in a five dimensional space [15] [16] . The multiplicative volume of the zero set would be a “Hausdorff” information or a Hausdorff five dimensional volume equal [12] [15] [16]
pre-wave surface, this time in a five dimensional space [15] [16] . The multiplicative volume of the zero set would be a “Hausdorff” information or a Hausdorff five dimensional volume equal [12] [15] [16]
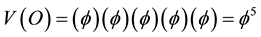 (2)
(2)
while the corresponding additive Hausdorff volume of its dual empty set surface would be [12] [15] [16]
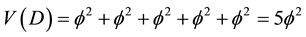 (3)
(3)
From the above it follows that the corresponding energy density would therefore obviously be [12] [15] [16] [20]
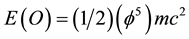 (4)
(4)
and
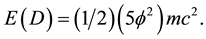 (5)
(5)
where E(O) could be likened with the stationary potential energy while E(D) could be likened with the kinetic energy of propagation in classical mechanics. Adding both energies together we found immediately the correct famous formula for the total energy of Einstein [15] [16] [20]
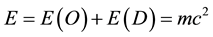 (6)
(6)
where E(O) is exactly equal 4.508497197 percent of the total energy and agrees in an astounding degree with cosmic measurements and observations while E(D) is equal to exactly 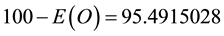 percent and equally in full agreement with measurements [8] [12] [16] . Needless to say this is also almost the same result obtained from applying the celebrated theorem of Dvoretzky [12] [23] . Now we are in a position to move on to considering the black hole information paradox [17] - [19] but we could mention on passing that equations 4 - 6 imply already a momentous conclusion, namely that dark energy is the global manifestation of the Casimir local effect [22] [23] .
percent and equally in full agreement with measurements [8] [12] [16] . Needless to say this is also almost the same result obtained from applying the celebrated theorem of Dvoretzky [12] [23] . Now we are in a position to move on to considering the black hole information paradox [17] - [19] but we could mention on passing that equations 4 - 6 imply already a momentous conclusion, namely that dark energy is the global manifestation of the Casimir local effect [22] [23] .
5. A Pointless and Self Referential Spacetime Resolution of the Black Hole Information Paradox
Let us examine the implicit assumptions in our previous exposition leading to the realization that dark energy is the energy of the quantum wave concentrated at the surface of the quantum particle universe. This was obtained using a model which de facto assumes that spacetime is a pointless and self referential fractal Cantorian ultimate L-like topological manifold where each point upon magnification reveals itself as an entire Cantor set, ergo an entire universe [12] [15] [16] . Thus our complete universe is a gigantic black hole in which we are peacefully living. Each point in this universe could be regarded as a quasi black hole seen from our end and there are of course “medium” sized black holes seen again from our view point as observer but self similarity or more accurately self affinity implies that these are again complete universes inside our universe seen again from our position as observer living in the gigantic black hole and so on ad infinitum [15] [21] . In short, the complexity of the situation uses the in-built self referentiality of Cantorian fractals [25] . That way infinity and zero are used and eliminated at the same time without getting entangled in computational or logical inconsistency. Finally invoking the well known relation between energy and information via entropy we see that the result obtained in our ordinary and dark energy investigation is applicable in duality to information. From our position the 96 percent information on the surface of the black hole could not be regarded in any way as lost, nor does it matter how small the black hole shrinks. Only the 4 percent information inside will not be directly accessible to us but it is not lost either. This is the perfect coincidentia oppositorium Hegelian resolution of the paradox while preserving a substantial part of the arguments of L. Susskind and Gerard tHooft [17] - [19] as well as some parts of Hawking’s thesis [13] and most importantly, all that is obtained without violating the fundamental laws of physics thanks to the idea of a self affine pointless Cantorian fractal universe [17] [18] [24] .
6. Conclusion
There is indeed a quantum particle universe corresponding to the Hartle-Hawking quantum wave of the universe. Using the self referentiality [25] of our pointless Cantorian fractal spacetime and applying Dvoretzky’s theorem to the compelling logic of this gigantic quantum particle universe, we can reason that E = mc2 can be split into a quantum wave energy density 

Cite this paper
Mohamed S.El Naschie,Mohamed S.El Naschie, (2015) If Quantum “Wave” of the Universe Then Quantum “Particle” of the Universe: A Resolution of the Dark Energy Question and the Black Hole Information Paradox. International Journal of Astronomy and Astrophysics,05,243-247. doi: 10.4236/ijaa.2015.54027
References
- 1. Hartle, J.B. and Hawking, S.W. (1983) Wave Function of the Universe. Physics Review D, 28, 2960-2975.
http://dx.doi.org/10.1103/PhysRevD.28.2960 - 2. Hawking, S. and Penrose, R. (1996) The Nature of Space and Time. Princeton University Press, Princeton, New Jersey.
- 3. Misner, C., Thorne, K. and Wheeler, J. (1973) Gravitation. Freeman, New York.
- 4. Hawking, S. (1993) Hawking on the Big Bang and Black Holes. World Scientific, Singapore.
- 5. Gibbons, G.W. and Hawking, S.W. (1993) Euclidean Quantum Gravity. World Scientific, Singapore.
http://dx.doi.org/10.1142/1301 - 6. Hawking, S. and Israel, W. (1990) 300 Years of Gravitation. Cambridge University Press, Cambridge, UK.
- 7. Tayler, E.F. and Wheeler, J.A. (1966) Spacetime Physics. W.H. Freeman Company, New York, USA.
- 8. Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observation. Cambridge University Press, Cambridge, UK.
http://dx.doi.org/10.1017/CBO9780511750823 - 9. Connes, A. (1994) Noncommutative Geometry. Academic Press, San Diego, USA.
- 10. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.
http://dx.doi.org/10.1007/s10773-014-2123-8 - 11. El Naschie, M.S. (1998) Von Neumann Geometry and E-Infinity Quantum Spacetime. Chaos, Solitons & Fractals, 9, 2023-2030.
- 12. El Naschie, M.S. (2014) The Measure Concentration of Convex Geometry in a Quasi Banach Spacetime behind the Supposedly Missing Dark Energy of the Cosmos. American Journal of Astronomy & Astrophysics, 2, 72-77.
http://dx.doi.org/10.11648/j.ajaa.20140206.13 - 13. Moskowitz, C. (2015) Stephen Hawking Hasn’t Solved the Black Hole Paradox Just Yet. Scientific American, 27 August 2015.
- 14. El Naschie, M.S. (2006) Fractal Black Holes and Information. Chaos, Solitons & Fractals, 29, 23-35.
http://dx.doi.org/10.1016/j.chaos.2005.11.079 - 15. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 16. El Naschie, M.S. (2013) What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy and Astrophysics, 3, 205-211.
http://dx.doi.org/10.4236/ijaa.2013.33024 - 17. Susskind, L. and Lindesay, J. (2005) Black Holes, Information and the String Theory Revolution. World Scientific, Singapore.
- 18. Susskind, L. (2008) The Black Hole War. Back Bay Books, New York.
- 19. ‘t Hooft, G. (1985) On the Quantum Structure of a Black Hole. Nuclear Physics B, 256, 727-745.
http://dx.doi.org/10.1016/0550-3213(85)90418-3 - 20. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entangled Origin. Journal of Quantum Information Science, 4, 284-291.
http://dx.doi.org/10.4236/jqis.2014.44023 - 21. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 22. El Naschie, M.S. (2015) Banach Spacetime-Like Dvoretzky Volume Concentration as Cosmic Holographic Dark Energy. International Journal of High Energy Physics, 2, 13-21.
http://dx.doi.org/10.11648/j.ijhep.20150201.12 - 23. Ball, K. (1997) An Elementary Introduction to Modern Convex Geometry. In: Levy, S., Ed., Flavors of Geometry, Cambridge University Press, Cambridge, 1-58.
- 24. Baryshev, Y. and Teerikorpe, P. (2002) Discovery of Cosmic Fractals. World Scientific, Hackensack.
- 25. Kauffman, L.H. (1987) Self-Reference and Recursive Form. Journal of Social and Biological Structures, 10, 53-72.
http://dx.doi.org/10.1016/0140-1750(87)90034-0 - 26. Hartle, J.B. and Hawking, S.W. (1983) Wave Function of the Universe. Physics Review D, 28, 2960-2975.
http://dx.doi.org/10.1103/PhysRevD.28.2960 - 27. Hawking, S. and Penrose, R. (1996) The Nature of Space and Time. Princeton University Press, Princeton, New Jersey.
- 28. Misner, C., Thorne, K. and Wheeler, J. (1973) Gravitation. Freeman, New York.
- 29. Hawking, S. (1993) Hawking on the Big Bang and Black Holes. World Scientific, Singapore.
- 30. Gibbons, G.W. and Hawking, S.W. (1993) Euclidean Quantum Gravity. World Scientific, Singapore.
http://dx.doi.org/10.1142/1301 - 31. Hawking, S. and Israel, W. (1990) 300 Years of Gravitation. Cambridge University Press, Cambridge, UK.
- 32. Tayler, E.F. and Wheeler, J.A. (1966) Spacetime Physics. W.H. Freeman Company, New York, USA.
- 33. Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observation. Cambridge University Press, Cambridge, UK.
http://dx.doi.org/10.1017/CBO9780511750823 - 34. Connes, A. (1994) Noncommutative Geometry. Academic Press, San Diego, USA.
- 35. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.
http://dx.doi.org/10.1007/s10773-014-2123-8 - 36. El Naschie, M.S. (1998) Von Neumann Geometry and E-Infinity Quantum Spacetime. Chaos, Solitons & Fractals, 9, 2023-2030.
- 37. El Naschie, M.S. (2014) The Measure Concentration of Convex Geometry in a Quasi Banach Spacetime behind the Supposedly Missing Dark Energy of the Cosmos. American Journal of Astronomy & Astrophysics, 2, 72-77.
http://dx.doi.org/10.11648/j.ajaa.20140206.13 - 38. Moskowitz, C. (2015) Stephen Hawking Hasn’t Solved the Black Hole Paradox Just Yet. Scientific American, 27 August 2015.
- 39. El Naschie, M.S. (2006) Fractal Black Holes and Information. Chaos, Solitons & Fractals, 29, 23-35.
http://dx.doi.org/10.1016/j.chaos.2005.11.079 - 40. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 41. El Naschie, M.S. (2013) What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy and Astrophysics, 3, 205-211.
http://dx.doi.org/10.4236/ijaa.2013.33024 - 42. Susskind, L. and Lindesay, J. (2005) Black Holes, Information and the String Theory Revolution. World Scientific, Singapore.
- 43. Susskind, L. (2008) The Black Hole War. Back Bay Books, New York.
- 44. ‘t Hooft, G. (1985) On the Quantum Structure of a Black Hole. Nuclear Physics B, 256, 727-745.
http://dx.doi.org/10.1016/0550-3213(85)90418-3 - 45. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entangled Origin. Journal of Quantum Information Science, 4, 284-291.
http://dx.doi.org/10.4236/jqis.2014.44023 - 46. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 47. El Naschie, M.S. (2015) Banach Spacetime-Like Dvoretzky Volume Concentration as Cosmic Holographic Dark Energy. International Journal of High Energy Physics, 2, 13-21.
http://dx.doi.org/10.11648/j.ijhep.20150201.12 - 48. Ball, K. (1997) An Elementary Introduction to Modern Convex Geometry. In: Levy, S., Ed., Flavors of Geometry, Cambridge University Press, Cambridge, 1-58.
- 49. Baryshev, Y. and Teerikorpe, P. (2002) Discovery of Cosmic Fractals. World Scientific, Hackensack.
- 50. Kauffman, L.H. (1987) Self-Reference and Recursive Form. Journal of Social and Biological Structures, 10, 53-72.
http://dx.doi.org/10.1016/0140-1750(87)90034-0

