International Journal of Astronomy and Astrophysics
Vol.04 No.04(2014), Article ID:51478,8 pages
10.4236/ijaa.2014.44051
Theoretical Deduction of the Hubble Law Beginning with a MoND Theory in Context of the ΛFRW-Cosmology
Nelson Falcon, Andrés Aguirre
Laboratory of Physics of the Atmosphere and the Outer Space, University of Carabobo, Valencia, Venezuela
Email: nelsonfalconv@gmail.com, aaguirre3@uc.edu.ve
Academic Editor: Luigi Maxmilian Caligiuri, University of Calabria, Italy
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 September 2014; revised 8 October 2014; accepted 3 November 2014
ABSTRACT
We deduced the Hubble law and the age of the Universe, through the introduction of the Inverse Yukawa Field (IYF), as a non-local additive complement of the Newtonian gravitation (Modified Newtonian Dynamics). As a result, we connected the dynamics of astronomical objects at great scale with the Friedmann-Robertson-Walker ΛFRW) model. From the corresponding formalism, the Hubble law can be expressed as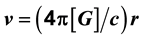 , which was derived by evaluating the IYF force at distances much greater than 50 Mpc, giving a maximum value for the expansion rate of the universe of
, which was derived by evaluating the IYF force at distances much greater than 50 Mpc, giving a maximum value for the expansion rate of the universe of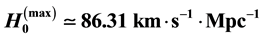 , consistent with the observational data of 392 astronomical objects from NASA/IPAC Extragalactic Database (NED). This additional field (IYF) provides a simple interpretation of dark energy as the action of baryonic matter at large scales. Additionally, we calculated the age of the universe as 11 Gyr, in agreement with recent measurements of the age of the white dwarfs in the solar neighborhood.
, consistent with the observational data of 392 astronomical objects from NASA/IPAC Extragalactic Database (NED). This additional field (IYF) provides a simple interpretation of dark energy as the action of baryonic matter at large scales. Additionally, we calculated the age of the universe as 11 Gyr, in agreement with recent measurements of the age of the white dwarfs in the solar neighborhood.
Keywords:
ΛFRW Cosmology, Hubble Law, MoND, Dark Energy

1. Introduction
The idea of a model for a universe in continuous and constant expansion emerged from the pioneering work of Hubble, Slipher and Humason [1] . This dynamic description of the universe began with early studies on relativistic cosmology [2] and is the foundation of the Big Bang theory, which explicitly uses the so-called Hubble law.
Hubble law was empirically proposed by Hubble [1] , who noted a roughly linear relation between velocities and distances among nebulae, and saw that the relation appears to dominate the distribution of velocities. The mathematical expression for this relation proposed by Hubble, so-called Hubblelaw, is usually written as
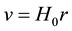 (1)
(1)
where 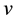 (in units of
(in units of ) is the recessional velocity of a given astronomical object, whose distance from the Earth, r, is measured in
) is the recessional velocity of a given astronomical object, whose distance from the Earth, r, is measured in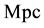 ,and
,and 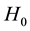 is the Hubble constant (in
is the Hubble constant (in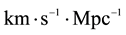 , that can be alternatively written as
, that can be alternatively written as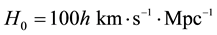 , where h is the dimensionless Hubble parameter and takes values between 0 and 1.
, where h is the dimensionless Hubble parameter and takes values between 0 and 1.
Since the discovery of the accelerating expansion of the universe through the study of high red shift supernovae [3] [4] , the current cosmological model uses the Hubble law together with Friedmann equations as the basis of the Standard Model of Big Bang cosmology. Friedmann equations constitute the solutions of the Einstein field equations of the General Theory of Relativity for the Friedmann-Robertson-Walker (FRW) metric under the additional assumption of the isotropic and homogeneous universe at large scales (Cosmological Principle).
Although Hubble law represents the first observational test of the expansion of the universe, and today supports the actual cosmological model [5] , it has not been theoretically deduced, so many hypotheses have arisen to this end, and even more new theories have emerged as alternative for the velocity-distance law. Among the alternatives is Browne [6] , who determined that Hubble law is a linear approximation of a more general exponential law, but it was conceived for a deSitter universe with no matter. Segal et al. [7] by studying IRAS data proposed asquare law, as given by Lundmark, however Strauss & Koranyi [8] reviewed Segal’s research and studied IRAS data too and determined that observations actually support Hubble law, the same result was obtained for galaxies from CfA and ESO/LV [9] . Pascual-Sánchez [10] determined a generalized Hubble law which introduces two additional terms to the usual Hubble law produced by the angular expansion, but this conception implies an anisotropic universe in conflicts with the Cosmological Principle. At this point, Hubble law has remained unalterable, and therefore the latest theories seem to look for deriving the velocity-distance law as was proposed by Hubble, namely, they look for a theoretical deduction of the Hubble law. Liu [11] derived the Hubble law under a hypothesis that eliminates the need for dark energy, nevertheless he used a non-conventional form of the FRW metric with the time defined as relative to some hypothetical time where the line element was or will be the Minkowskian, which has not been found by observations. Sorrell [12] proposed that Hubble law, as result of an expanding universe, is really a working hypothesis, instead he considered the hypothesis proposed by Zwicky of the tired-light, but nowadays it is well known that this theory is not supported by observations, in fact it does not explain theanisotropies in the CMB. Recently, Sanejouand [13] opted for a non-standard form of the Hubble law, assuming a new definition of the red shift based infrequencies rather than wavelength, establishing a new paradigm for the spectroscopy.
One of the biggest problems in the Big Bang cosmology, closely linked to the expansion of the Universe and the Hubble law, is the evidence of the accelerated expansion of the Universe, commonly referred as dark energy, whose understanding is still far from complete. Also, the inconsistency between the observed average density of matter and the density required for flatness of the universe, a problem known as the missing mass, has become the paradigm of the hypothetical non-baryonic dark matter. This discrepancy between the astronomical observations of the density of matter and expected in ΛFRW model in the Big Bang theory, has prevailed in the last years. An alternative to the paradigm of non-baryonic dark matter is the theory of Modified Newtonian Dynamics (MoND), which involve changes in the Newton’s law of gravitation (inverse square law).
In this sense, one possibility to solve both problems: dark matter and dark energy, is the non-local gravitation recently proposed by Falcón [14] , which basically is a MoND theory. According to which the force of gravitation would be the result of two fields generated by the ordinary baryonic matter, a first term as Newton law of the inverse square and an additional long-range term.
The inclusion of this second term in the force of gravity, consistent with Eötvös-like experiments, can reconcile the ΛFRW model with observables of the Big Bang, without the paradigm of non-baryonic dark matter. Additionally, gives an explanation for dark energy, and allows us to theoretically deduce the Hubble law.
In this paper, we will show that the Hubble law can be derived from the MoND theory proposed by Falcón in a natural way through the corresponding condition of cosmological scales. To this end, in Section 2 we will review the paper of Falcón emphasizing the repulsive behavior of the non-local gravitational field at large scales, giving a starting point for deducting the Hubble law. The theoretical deduction of the Hubble law and even an analytical determination of the Hubble constant will be given in Section 3. In Section 4, we will contrast the determined Hubble constant with the observational data of 392 objects selected from the NASA/IPAC Extragalactic Database (NED), also a brief discussion about the cosmic age problem is given. Finally, the conclusions are given in Section 5.
2. MoND with Non-Local Gravitational Term
Current Big Bang cosmology assumes Newtonian gravitation as the only fundamental force at astronomical scales, giving a complete determination of the dynamics of the universe. However, from this idea we face serious difficulties to describe the behavior of the Universe: 1) galaxy rotation curves are not explained without the inclusion of non-baryonic dark matter, whose fundamental nature and properties are completely unknown; 2) into the rich galaxy clusters, the observed mass of stars and the gas mass inferred from the X-ray diffuse emission is significantly less than that required to hold these systems gravitationally stable; and 3) the accelerated expansion of the universe violates our understanding about how gravity works at cosmological scales (see [14] for details).
The simplest way for modeling the accelerated cosmic expansion is by introducing a cosmological constant into the Einstein’s field equations so it can represent a hypothetical negative pressure of the vacuum of space, also called dark energy. However this is given as a disconnected idea from the dynamics of the astronomical objects, which is limited to the Newton’s law of gravitation.
While Newtonian gravitation (inverse square law) has been highly supported by laboratory experiments and satellites, there is no experimental evidence to confirm its validity beyond the Solar System [15] . That is why it has raised the Modified Newtonian Dynamics (MoND) theories such as proposed by Milgrow [16] that solves the galaxy rotation problem originating from non-baryonic dark matter. Following this line, Falcón [14] [17] proposed a modification of the Newtonian gravitation by adding a non-local term that contains Milgrow’s theory as a particular case and establishes a possible connection for the dynamics at large scale and FRW formalism. This additional term was constructed by the specular reflection of the potential of Yukawa, so that we decided to named it: Inverse Yukawa Field (IYF). This interaction is given by the baryonic matter (as the Newtonian gravity), and shows a null contribution at scale of the Solar System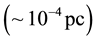 , in agreement with measurements on Earth, weakly attractive at interstellar distances
, in agreement with measurements on Earth, weakly attractive at interstellar distances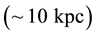 , consistent with MoND theory (as a solution of the galaxy rotation problem), strongly attractive at scales of galaxy clusters
, consistent with MoND theory (as a solution of the galaxy rotation problem), strongly attractive at scales of galaxy clusters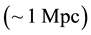 , in accordance with Abell radius, and repulsive at cosmological scales
, in accordance with Abell radius, and repulsive at cosmological scales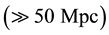 , in agreement with the expansion of the universe (see Figure 1). This interaction has a potential per unit of mass of the form
, in agreement with the expansion of the universe (see Figure 1). This interaction has a potential per unit of mass of the form
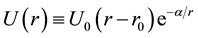 (2)
(2)
where 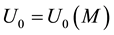 is the magnitude of the potential (in units of
is the magnitude of the potential (in units of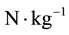 ) as a function of the baryonic matter,
) as a function of the baryonic matter, 

Then, the proposed modification considers the contribution of both the Newtonian and the non-local gravitational field, so that the dynamics at all scales is determined by the force per unit of mass as
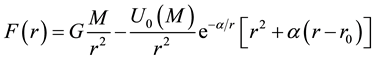
where it is important to note that there is a dependence on the baryonic matter only.
In particular, a zero contribution of the non-local term can be verified at distances below


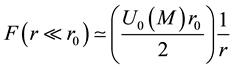
solving the galaxy rotation problem. Also, the non-local IYF, evaluated in the Abell radius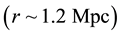
From Figure 1, it is clear that IYF potential gives a constant repulsive force at cosmological scales 
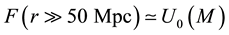
providing an asymptotic cosmic acceleration, consistent with the observations. This opens the possibility to describe the behavior of the cosmological constant by setting it as a dynamical term with the form 

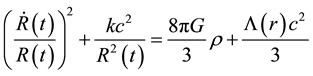

where the dot denotes the time derivate of the scale factor
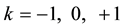
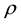
The introduction of the non-zero contribution of the cosmological constant brings a modification to the usual form of the matter density parameter, 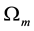

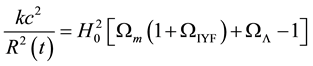
where the dark energy density parameter (or cosmological density parameter), 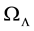
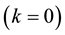
For a complete interpretation of the behavior of the IYF potential and details about the cosmological consequences by adding the IYF to Newtonian dynamics and to FRW cosmology see [14] . Finally, the repulsive behavior of this non-local term provides an starting point for studying the dynamics at large scale, and therefore for deducting theoretically the Hubble law.
3. Theoretical Deduction of Hubble Law
A numerical value for 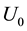
Figure 1. IYF potential per unit of mass as function of the distance between objects gravitationally bounded (see [14] for details).
Usually, the Poisson equation is written for the Newtonian gravitational case as
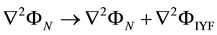
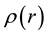

with 

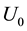



and the same for the matter density
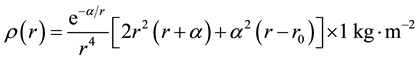
taking into account that this equality works for
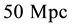
Here, we note that the obtained magnitude, 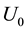
On the other hand, in Section 2 we saw that the IYF, as anon-local term, shows a repulsive behavior at cosmological scales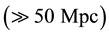
Consider a particle (galaxy, galaxy cluster, nebulae, etc.) with nonzero rest mass under the influence of the IYF force. The contribution of the Newtonian gravitational force is not important at cosmological scales (i.e. at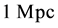


where 

Then, it is possible to obtain an expression of the velocity by integrating Equation (12) as follow


of the particle. Therefore,

With 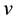

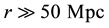
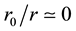


where without loss of generality we assumed the initial condition 


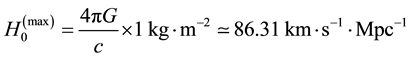
so that the Hubble law can be written as

Note that Equation (16) basically is equal to Equation (1), establishing a linear relation between recessional velocities and distances for a given particle (galaxy, cluster of galaxy, nebulae, etc.), just under the assumption of cosmological scales, in agreement with the current cosmological model. Additionally, the limit value of the linearly constant gives the maximum expansion rate of the universe, again as product ofstudy distances much greater than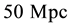
In the next section, we will test the 
4. Observational Test and Discussions
Although the first determination of the Hubble constant was 

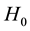
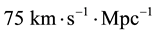

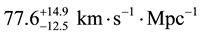

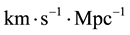
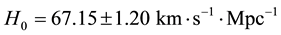
In this section, we will contrast our value for the Hubble constant, of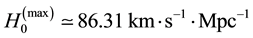
In order to verify the Hubble law and our value for the Hubble constant, we will use the primitive technique used by Hubble, which consists in plotting the observational measurements of the velocity (via red shift) and the distance of a set of objects such as galaxies, quasars, radio sources, X-ray sources, infrared sources, etc. For this end, we considered the Master List of Redshift-Independent Extragalactic Distances of 15339 galaxies provided by NED (Version 9.2.0). The observational measurements were filtered by: 1) recent measurements (year of publication from 2009); 2) distantobjects

A Hubble diagram for the 392 galaxies, in a range of 50 - 1400 Mpc, is shown in Figure 2. Through a linear fit we found that 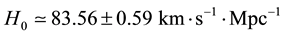

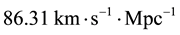
In Figure 2, we additionally note that the data suggest a lower slope for distances lower than 500 Mpc. Actually, a linear fit at that scales gives a Hubble constant of 
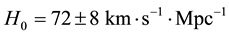

On the other hand, an additional result can be obtained through the determined Hubble constant: the age of the universe, 
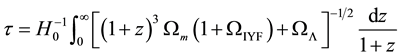
[14] , where 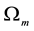
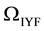

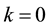
Figure 2. Hubble diagram for objects at 50 - 1400 Mpc (data from NED).
when the IYF is zero.
Numerical integration of Equation (17), for
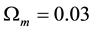
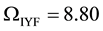
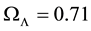
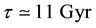
5. Conclusions
The inclusion of a long-range component in the law of gravitation allows linking the Hubble law with the dynamics of the large-scale Universe. Particularly, if the non-locality of gravitation is included through apotential as shown here, Yukawa Inverse type, we can connect the dark energy with cosmological constant and derive from there the Hubble law, consistent with the formalism of the Big Bang, and astronomical observations, without resorting to the paradigm of non-baryonic dark matter, or an “exoticphysics”.
The inclusion of a long-range component in the law of gravitation, through an inverse potential Yukawa-like, represents the collective contribution of the gravitational effects of large-scale, on the order of tens of megaparsec caused by ordinary baryonic matter. In this sense, the IYF explicitly includes the Mach principle in the formalism of FRW cosmology, as Einstein pretended with the Theory of General Relativity.
The prescription of the Hubble constant in terms of the fundamental constants, as in Equation (15), appears to correspond to the observational data for distant objects, whose distance and red shift are independently known; as we can see in Figure 2. Note that the Hubble constant is not measured directly by the WMAP and Planck sa- tellites, but rather its value is inferred from the power spectrum of the cosmic background radiation (CMB) to- gether with other cosmological variables through multiple statistics correlation, or maximum likelihood.
For the nearest objects, with distances less than a hundred megaparsec, the Hubble constant would seem less than true value, because in these ranges, the contribution of the IYF field is less, as was shown in Figure 1.
A current Hubble constant 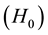

Acknowledgements
This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Cite this paper
NelsonFalcon,AndrésAguirre, (2014) Theoretical Deduction of the Hubble Law Beginning with a MoND Theory in Context of the ΛFRW-Cosmology. International Journal of Astronomy and Astrophysics,04,551-559. doi: 10.4236/ijaa.2014.44051
References
- 1. Hubble, E. (1929) A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae. Proceedings of the National Academy of Sciences, 15, 168-173.
http://dx.doi.org/10.1073/pnas.15.3.168 - 2. Lemaitre, G. (1927) A Homogeneous Universe of Constant Mass and Increasing Radius Accounting for the Radial Velocity of Extra-Galactic Nebulae. Annales de la Société Scientifique de Bruxelles, 47, 49-59.
- 3. Riess, A. G., et al.(1998) Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal, 116, 1009-1038.
http://dx.doi.org/10.1086/300499 - 4. Perlmutter, S., et al. (1999) Measurements of Ω and Λ from 42 High-Redshift Supernovae. The Astrophysical Journal, 517, 565-586. http://dx.doi.org/10.1086/307221
- 5. Freedman, W. and Madore, B. (2010) The Hubble Constant. Annual Review of Astronomy and Astrophysics, 48, 673-710. http://dx.doi.org/10.1146/annurev-astro-082708-101829
- 6. Browne, P.F. (1962) The Case for an Exponential Redshift Law. Nature, 193, 1019-1021.
http://dx.doi.org/10.1038/1931019a0 - 7. Segal, I.E., Nicoll, J.F., Wu, P. and Zhou, Z. (1993) Statistically Efficient Testing of the Hubble and Lundmark Laws on IRAS Galaxy Samples. The Astrophysical Journal, 411, 465-484.
http://dx.doi.org/10.1086/172849 - 8. Strauss, M. and Koranyi, D. (1993) Tests of the Hubble Law from the Luminosity Function of IRAS Galaxies. arXiv:astro-ph/9308028
- 9. Choloniewski, J. (1995) New Test for the Hubblelaw. arXiv:astro-ph/9504035
- 10. Pascual-Sánchez, J.-F. (2000) A Generalized Linear Hubble Law for an Inhomogeneous Barotropic Universe. arXiv:gr-qc/0010076
- 11. Liu, J.M. (2005) Modified Hubble Law, the Time-Varying Hubble Parameter and the Problem of Dark Energy. arXiv:physics/0507018 [physics.gen-ph]
- 12. Sorrell, W.H. (2009) Misconceptions about the Hubble Recession Law. Astrophysics and Space Science, 323, 205-211. http://dx.doi.org/10.1007/s10509-009-0057-z
- 13. Sanejouand, Y.H. (2014) A Simple Hubble-Like Lawin Lieu of Dark Energy. arXiv:1401.2919 [astro-ph.CO]
- 14. Falcón, N. (2013) Modification of the Newtonian Dynamics in ΛFRW-Cosmology an Alternative Approach to Dark Matter and Dark Energy. Journal of Modern Physics, 4, 10-18.
http://dx.doi.org/10.4236/jmp.2013.48A003 - 15. Gundlach, J.H. (2005) Laboratory Tests of Gravity. New Journal of Physics, 7, 205.
http://dx.doi.org/10.1088/1367-2630/7/1/205 - 16. Milgrom, M. (1983) A Modification of the Newtonian Dynamics: Implications for Galaxies. The Astrophysical Journal, 270, 371-389. http://dx.doi.org/10.1086/161131
- 17. Falcón, N. (2011) MoND with Einstein’s Cosmological Term as Alternative to Dark Matter. Revista Mexicana de Astronomía y Astrofísica (Serie de Conferencias), 40, 11-12.
- 18. Turyshev, S.G. and Toth, V.T. (2010) The Pioneer Anomaly. Living Reviews in Relativity, 13, 4. http://dx.doi.org/10.12942/lrr-2010-4
- 19. Sandage, A. (1958) Currents Problems in the Extragalactic Distance Scale. The Astrophysical Journal, 127, 513-526. http://dx.doi.org/10.1086/146483
- 20. Freedman, W., Madore, B.F., Gibson, B.K., Ferrarese, L., Kelson, D.D., Sakai, S., et al. (2001) Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. The Astrophysical Journal, 553, 47-72. http://dx.doi.org/10.1086/320638
- 21. Bonamente, M., Joy, M.K., LaRoque, S.J., Carlstrom, J.E., Reese, E.D. and Dawson, K.S. (2006) Determination of the Cosmic Distance Scale from Sunyaev-Zel’dovich Effect and Chandra X-Ray Measurements of High-Redshift Galaxy Clusters. The Astrophysical Journal, 647, 25-54.
http://dx.doi.org/10.1086/505291 - 22. Bennett, C., Larson, D., Weiland, J.L., Jarosik, N., Hinshaw, G., Odegard, N., et al. (2012) Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. The Astrophysical Journal Supplement Series, 208, 20. http://dx.doi.org/10.1088/0067-0049/208/2/20
- 23. Ade, P.A.R., Aghanim, N., Alves, M.I.R., Armitage-Caplan, C., Arnaud, M., Ashdown, M., et al. (2013) Planck 2013 Results. I. Overview of Products and Scientific Results. arXiv:1303.5062 [astro-ph.CO]
- 24. Blakeslee, J., Lucey, J., Barris, B., Hudson, M. and Tonry, J. (2001) A Synthesis of Data from Fundamental Plane and Surface Brightness Fluctuation Surveys. Monthly Notices of the Royal Astronomical Society, 327, 1004-1020. http://dx.doi.org/10.1046/j.1365-8711.2001.04800.x
- 25. Freedman, W. and Turner, M. (2003) Colloquium: Measuring and Understanding the Universe. Review of Modern Physics, 75, 1433-1447. http://dx.doi.org/10.1103/RevModPhys.75.1433
- 26. Tremblay, P.E., Kalirai, J.S., Soderblom, D.R., Cignoni, M. and Cummings, J. (2014) White Dwarf Cosmochronology in the Solar Neighborhood. arXiv:1406.5173 [astro-ph.SR]
- 27. Wang, S., Li, X. and Li, M. (2010) Revisit of Cosmic Age Problem. Physical Review D, 82, 103006. http://dx.doi.org/10.1103/PhysRevD.82.103006



