International Journal of Astronomy and Astrophysics
Vol.4 No.2(2014), Article ID:45068,13 pages DOI:10.4236/ijaa.2014.42026
Stability of Accretion Discs around Magnetised Stars
Solomon Belay Tessema1,2
1Department of Physics, Kotebe University College, Addis Ababa, Ethiopia
2Astronomy and Astrophysics Research Division, Entoto Observatory and Research Center, Addis Ababa, Ethiopia
Email: tessemabelay@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 5 February 2014; revised 1 March 2014; accepted 9 March 2014
ABSTRACT
We study the stability of accretion disc around magnetised stars. Starting from the equations of magnetohydrodynamics we derive equations for linearized perturbation of geometrically thin, optically thick axisymmetric accretion disc with an internal dynamo around magnetized stars. The structure and evolution of such discs are governed by an evolution equation for matter surface density ∑(R, t). Using the time-dependent equations for an accretion disc we do a linear stability analysis of our steady disc solutions in the presence of the magnetic field generated due to an internal dynamo.
Keywords:Accretion, Accretion Discs, Instabilities, Stability, Magnetic Fields, MHD, Stars, Neutron, X-Rays, Binaries

1. Introduction
After the establishment of the standard thin accretion disc model by [1] , its stability has become an important area in the accretion disc theory. Since instabilities of accretion discs permit to explain the observed phenomena of variability and luminosity of various astronomical objects, such as X-ray binaries, black holes, active galactic nuclei, etc., many authors have carried out studies on the instabilities of accretion discs using standard model. [2] found that in the innermost regions of accretion discs around stellar mass neutron stars or black holes, where electron scattering is the dominant source of opacity and radiation pressure is much greater than gas pressure, the disk flow would be viscously unstable if radiation pressure was to determine the magnitude of viscosity in the 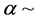 prescription. Subsequently, numerous authors generalized this stability analysis and showed that these inner regions of the disc may also be thermally unstable (e.g. [3] and [4] ). However, these analyses dealt primarily with the evolution of small perturbations of the disc’s central temperature
prescription. Subsequently, numerous authors generalized this stability analysis and showed that these inner regions of the disc may also be thermally unstable (e.g. [3] and [4] ). However, these analyses dealt primarily with the evolution of small perturbations of the disc’s central temperature 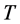 and surface density
and surface density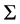 . [5] undertook a more general stability analysis by considering the evolution of infinitesimal perturbations of all three components of the fluid velocity as well as temperature,
. [5] undertook a more general stability analysis by considering the evolution of infinitesimal perturbations of all three components of the fluid velocity as well as temperature, 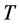 and surface density
and surface density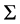 , and he found that the disc also exhibited pulsational instability besides the viscous and thermal instability. [6] generalized Kato’s analysis by considering the pulsation stability criterion for a thin disk model with different ratios of gas to radiation pressure, arbitrary values of
, and he found that the disc also exhibited pulsational instability besides the viscous and thermal instability. [6] generalized Kato’s analysis by considering the pulsation stability criterion for a thin disk model with different ratios of gas to radiation pressure, arbitrary values of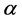 , a general functional form for the viscosity. Chem and Tamm (1993) performed a numerical study on the structure and stability of accretion discs, taking into consideration radial velocity. They showed that the radial velocity has a stabilizing influence on the viscous mode. Wu Xuebing et al. (1994) and Yu Wenfei et al. (1994) considered the influence of radial velocity on the stability of a polytropic and an isothermal magnetised accretion disc, respectively. Thermal instability results from the inability of local heating and cooling mechanisms to efficiently maintain a thermal balance, while the viscous instability results from a negative diffusion coefficient which amplifies density contrasts. In the former case the inner region of the disc tends to break up into concentric rings. In circumstances where the disc is unstable to both thermal and surface density perturbations, thermal stability determines the evolution of the disc since its corresponding growth time is shorter.
, a general functional form for the viscosity. Chem and Tamm (1993) performed a numerical study on the structure and stability of accretion discs, taking into consideration radial velocity. They showed that the radial velocity has a stabilizing influence on the viscous mode. Wu Xuebing et al. (1994) and Yu Wenfei et al. (1994) considered the influence of radial velocity on the stability of a polytropic and an isothermal magnetised accretion disc, respectively. Thermal instability results from the inability of local heating and cooling mechanisms to efficiently maintain a thermal balance, while the viscous instability results from a negative diffusion coefficient which amplifies density contrasts. In the former case the inner region of the disc tends to break up into concentric rings. In circumstances where the disc is unstable to both thermal and surface density perturbations, thermal stability determines the evolution of the disc since its corresponding growth time is shorter.
The Balbus-Hawley (magnetorotational) instability of weak magnetic fields in accretion discs drives MHD turbulence which transports angular momentum radially outwards ([7] [8] ), and is thought to play an important role in the evolution and dynamics of astrophysical accretion discs. The instability has also been invoked as a component of a disc dynamo model, in which the instability creates radial field from vertical field, the shear in the disc creates azimuthal field from the radial component, and the Parker instability creates vertical from azimuthal field and expels flux from the disc [9] .
[10] hereafter Paper I, have investigated the interaction between magnetic neutron star and its surrounding accretion disc in the case where the accretion disc is supporting an internal dynamo. They introduced a new solution for an accretion disc around a magnetic star. [11] , hereafter Paper II, have also studied the thin accretion disc around millisecond X-ray pulsars, which is the extension of Paper I. In both Papers they have developed a model for steady-state disc and found that the torque generated by the internal dynamo is stronger than the torque generated due to the shear.
The purpose of the present work is to study the time dependent behavior of thin, axisymmetric accretion disc with an internal dynamo around magnetised stars. This will be used to determine the stability properties of our disc model which has been developed in Paper I & II. We work in the spirit of [1] & [4] and Paper I & II and assume that the disc is geometrically thin and optically thick. In Section 2 we start from the equation of magnetohydrodynamics and derive basic time dependent equations. We then present the modified diffusion equation and its analysis in Section 3 and discuss the stability properties of our disc model in Section 4. Finally we summarize our conclusion in Section 5.
2. Basic Time-Dependent Equations of Accretion Disc
In order to study the temporal behavior of the disc we derive basic time-dependent equations for a thin axisymmetric Keplerian disc around a magnetized star with a magnetic dipole field. The basic equations describing the time-dependent accretion disc can be derived from the equations of magnetohydrodynamics. The dynamical equations for steady state axisymmetric accretion flows we consider here are usual in (paper I & II). Our approach is an extension of the standard model for a thin accretion disc [1] , and it follows closely the method that we introduced in Paper I & II, though we will now consider general time-dependent equations around magnetised stars.
2.1. Equation of Continuity
We start with the conservation of mass, which we have already introduced in the steady-state case
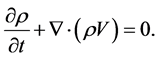 (1)
(1)
where ![]() is the density and
is the density and 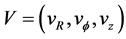 is the fluid velocity with radial, azimuthal and vertical components, respectively.
is the fluid velocity with radial, azimuthal and vertical components, respectively.
For a thin axisymmetric disc integrating (1) vertically and neglecting a vertical outflow from the disc we get
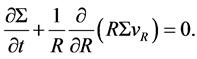 (2)
(2)
where 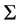 is the surface density.
is the surface density.
 (3)
(3)
where 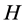 is the half-thickness of the disc at any given radius, while
is the half-thickness of the disc at any given radius, while ![]() is the volume density. The variation in the surface density at radius R conforms to the equation of continuity and gives
is the volume density. The variation in the surface density at radius R conforms to the equation of continuity and gives
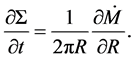 (4)
(4)
where 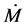 represents the mass transfer rate at each radius given by
represents the mass transfer rate at each radius given by
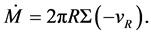 (5)
(5)
2.2. Equation of Momentum Transfer
The time-dependent version of the angular momentum transferred per unit mass of a fluid can be derived from the Navier-Stoke’s equation and rewritten in general as
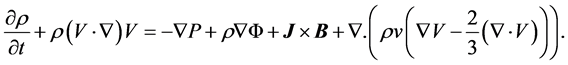 (6)
(6)
where 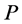 pressure,
pressure,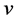 kinetic viscosity,
kinetic viscosity, 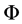 the gravitational potential
the gravitational potential  the current density and
the current density and 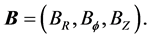 the magnetic field. The viscosity in general is small, and we will only retain it where it plays a crucial role. The radial component of Navier-Stoke’s equation is
the magnetic field. The viscosity in general is small, and we will only retain it where it plays a crucial role. The radial component of Navier-Stoke’s equation is
 (7)
(7)
For a thin accretion disc  as shown below and the dominant terms of the equation give us that
as shown below and the dominant terms of the equation give us that
 (8)
(8)
this shows that the disc rotates in a Keplerian fashion. That is the matter in the disc approximately flows along circular Keplerian orbits with this velocity.
The vertical component of the time dependent momentum transfer equation is
 (9)
(9)
Neglecting vertical outflows since the motion in the disc along the z-direction are subsonic and assuming the magnetic field to be weak the equation reduces to the equation of hydrostatic equilibrium
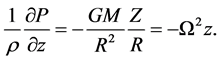 (10)
(10)
Using the above equation the pressure is
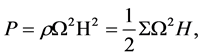 (11)
(11)
but the hydrostatic equilibrium can also be expressed as
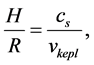 (12)
(12)
which shows that the Keplerian velocity is highly supersonic in a thin accretion disc assumed above, where
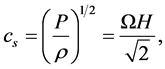 (13)
(13)
is the isothermal speed of sound. For a thin disc 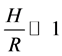 this can only be true if
this can only be true if 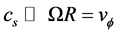 that is the radial derivative of pressure is small compared with gravitational and centrifugal forces.
that is the radial derivative of pressure is small compared with gravitational and centrifugal forces.
The angular momentum transport can be found from the azimuthal component of Navier-Stoke’s equation (see Paper I & II) for detail derivations:
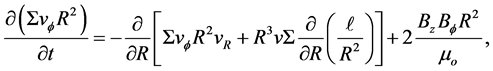 (14)
(14)
We neglect  because the large-scale poloidal magnetic field is the stellar dipole field, which has only a vertical component in the stellar equatorial plane. Using continuity equation and assuming that
because the large-scale poloidal magnetic field is the stellar dipole field, which has only a vertical component in the stellar equatorial plane. Using continuity equation and assuming that
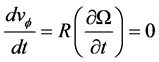 . Then the conservational angular momentum given by Equation (14) leads to the following height-integrated equation
. Then the conservational angular momentum given by Equation (14) leads to the following height-integrated equation
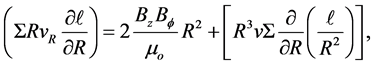 (15)
(15)
where the right-hand side of Equation (15) accounts for the radial advection of angular momentum owing to the viscous and the magnetic torques. The magnetic term describes the exchange of angular momentum between the disc and the star via magnetosphere.
We assume that the vertical magnetic field is due to the dipolar field of the neutron star, so that its value in the equatorial plane is
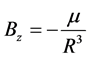 (16)
(16)
where ![]() is the magnetic dipole moment of the star.
is the magnetic dipole moment of the star.
This term vanishes if  is an even function of
is an even function of , but the shear between the disc and the stellar magnetosphere generates an odd
, but the shear between the disc and the stellar magnetosphere generates an odd 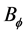 whose value in the upper half of the disc is
whose value in the upper half of the disc is
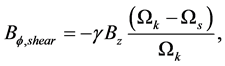 (17)
(17)
where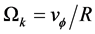 ,
, 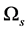 is the angular velocity of the star,
is the angular velocity of the star, ![]() is a dimensionless parameter of the order of a few [12] [13] . We now add an extra large-scale toroidal field, which is generated by an internal dynamo in the accretion disc.
is a dimensionless parameter of the order of a few [12] [13] . We now add an extra large-scale toroidal field, which is generated by an internal dynamo in the accretion disc.
Such a dynamo is a natural consequence of the magnetohydrodynamic turbulence in the accretion disc [14] . In order to estimate the size of 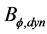 we will for the moment assume that the viscous stress in the accretion disc is due to the internal magnetic stress
we will for the moment assume that the viscous stress in the accretion disc is due to the internal magnetic stress
 (18)
(18)
where we use the [1] prescription for the viscosity in the last equality. Based on the results of numerical simulations of magnetohydrodynamic turbulence in the accretion discs (e.g. [15] [16] ) argued that
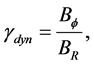 (19)
(19)
where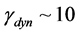 . However this
. However this  is the sum of the large-scale field and small-scale turbulent field, which is also contributing to stress
is the sum of the large-scale field and small-scale turbulent field, which is also contributing to stress 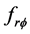 through its correlation with a turbulent
through its correlation with a turbulent 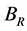 -field. Since the large-scale field might be a small fraction of the total field we multiply
-field. Since the large-scale field might be a small fraction of the total field we multiply  with a factor ϵ to get an estimate for
with a factor ϵ to get an estimate for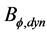 :
:
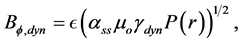 (20)
(20)
where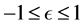 , and a negative value describes a magnetic field which is pointing in the negative
, and a negative value describes a magnetic field which is pointing in the negative  -direction at the upper disc surface. We now replace the
-direction at the upper disc surface. We now replace the  in Equation (15) with the sum of the toroidal fields that are generated by the shear, Equation (17), and the internal dynamo, Equation (20) gives
in Equation (15) with the sum of the toroidal fields that are generated by the shear, Equation (17), and the internal dynamo, Equation (20) gives
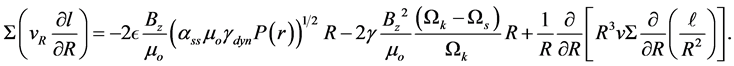 (21)
(21)
Solving Equation (15) for radial velocity yields
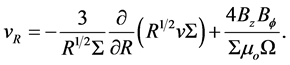 (22)
(22)
Inserting Equation (22) into continuity equation, then the equation for the evolution of the surface density 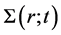 of the accretion disc for the disc around the magnetised star can be found as
of the accretion disc for the disc around the magnetised star can be found as
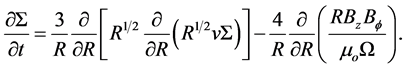 (23)
(23)
Equation (23) is an integral of the mass and angular momentum equations which is more general, and relies on the assumptions: conservation of mass, conservation of angular momentum, and that the potential is Keplerian. Since the time dependence enters only through Equation (23), it is essential to try to express the other quantities in terms of  as far as possible, as they depend on t only through
as far as possible, as they depend on t only through 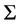 and not explicitly.
and not explicitly.
2.3. Dissipation of Energy in the Disc
The Navier-Stoke’s equation for the conservation of internal energy can be written as:
 (24)
(24)
Here the second term on the left describes the variations in the internal energy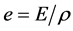 , while the first and third terms in the right-hand-side describes viscous heating and radiative cooling respectively and the second and fourth terms are respectively ohmic heating and heat conduction. Neglecting very small terms and retaining the dominant terms, then the energy equation gives
, while the first and third terms in the right-hand-side describes viscous heating and radiative cooling respectively and the second and fourth terms are respectively ohmic heating and heat conduction. Neglecting very small terms and retaining the dominant terms, then the energy equation gives
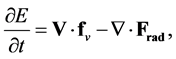 (25)
(25)
Integrating Equation (25) vertically over the disc we have
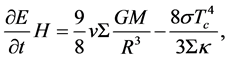 (26)
(26)
This is the conservation of energy.
The optical depth of the disc is given by :
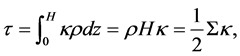 (27)
(27)
where κ is the general opacity given by
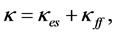 (28)
(28)
where 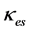 is electron scattering opacity equal to
is electron scattering opacity equal to
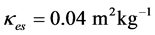 (29)
(29)
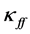 is free-free absorption given by Kramer’s law
is free-free absorption given by Kramer’s law
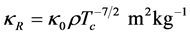 (30)
(30)
with
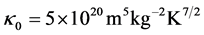 .
.
2.4. Equation of State
The total pressure is the sum of gas pressure and radiation pressure and then given by the equation of state:
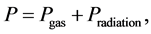 (31)
(31)
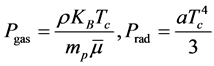 (32)
(32)
In Equation (32), 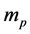 ,
, 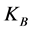 ,
,  , and
, and 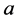 are the mass of a proton, Boltzmann constant, the mean molecular weight for ionized gas, and familiar radiation constant, respectively. We can write Equation (31) as
are the mass of a proton, Boltzmann constant, the mean molecular weight for ionized gas, and familiar radiation constant, respectively. We can write Equation (31) as
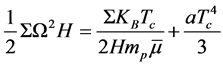 (33)
(33)
2.5. Viscous Stress
In our model the viscous stress tensor is related according to
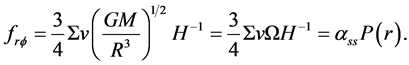 (34)
(34)
The conventional  model assumes that
model assumes that
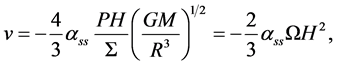 (35)
(35)
where 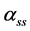 is a viscous parameter which describes the strength of the viscous stress.
is a viscous parameter which describes the strength of the viscous stress.
From Equation (35) the internal pressure becomes
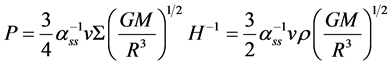 (36)
(36)
Which we solve for the density of the gas
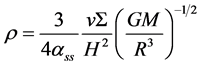 (37)
(37)
3. Viscous Stability
Viscous stability of geometrically thin, optically thick, Keplerian accretion disc is described by the evolution of the discs surface density which is obtained by combining the conditions of conservation of mass and angular momentum. In our model this is the equation for the evolution of the surface density Σ of an accretion disc around a magnetized star as shown in Equation (23) where  is the sum of the magnetic field generated by the internal dynamo and due to shear. Equation (38) is a diffusion equation in the presence of magnetic field which gives the evolution of the surface density function, due to the spreading of material controlled by viscous and magnetic stresses.
is the sum of the magnetic field generated by the internal dynamo and due to shear. Equation (38) is a diffusion equation in the presence of magnetic field which gives the evolution of the surface density function, due to the spreading of material controlled by viscous and magnetic stresses.
It is clear that in order to solve non-linear Equation (23) and subsequently find all the other disc variables is in general a formidable task which must be solved numerically which will not be considered in this paper for the moment. However, we can draw important conclusions relating different equations and the form of Equation (23) alone. Suppose the viscous  varies as given power of radius the equation can be solved analytically. Assuming that the viscosity at a given radius depend on local parameters in the disc. In its simplest form we may write
varies as given power of radius the equation can be solved analytically. Assuming that the viscosity at a given radius depend on local parameters in the disc. In its simplest form we may write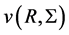 . For convenience we write
. For convenience we write
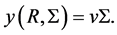 (38)
(38)
We further assume that the surface density in a steady disc is perturbed axisymmetrically at each radius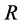 , so that
, so that
 (39)
(39)
where 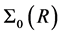 is the steady-state distribution and let the corresponding perturbation for
is the steady-state distribution and let the corresponding perturbation for ![]() be
be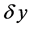 , then
, then
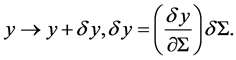 (40)
(40)
Taking similar perturbations in the toroidal magnetic field generated by the internal dynamo  and substituting in diffusion equation yields the linear equation
and substituting in diffusion equation yields the linear equation
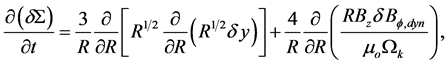 (41)
(41)
where,
 (42)
(42)
Here the shear component of the magnetic field is very small and dropped. Thus a small perturbation δy satisfies the linear equation
 (43)
(43)
where,
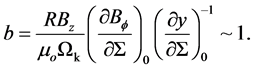 (44)
(44)
Equation (43) is a linear modified diffusion equation for , which describes the evolution of a perturbation in
, which describes the evolution of a perturbation in ![]() and well behaved if and only if the modified diffusion coefficient is positive. When the coefficient
and well behaved if and only if the modified diffusion coefficient is positive. When the coefficient 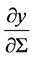
is positive we have the evolution equation of the type of diffusion equation behavior including magnetic stress.
However, if  is negative, more material will be fed into those regions of the disc that are denser than their surroundings and material will be removed from those regions that are less dense so that the disc will tend to break up into rings and this breakup of on viscous time scale constitutes the viscous instability; steady disc flow is only possible provided that
is negative, more material will be fed into those regions of the disc that are denser than their surroundings and material will be removed from those regions that are less dense so that the disc will tend to break up into rings and this breakup of on viscous time scale constitutes the viscous instability; steady disc flow is only possible provided that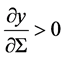 .
.
If a disc is viscously unstable, a region that is locally under dense (over dense) evolves faster (slower) than its surroundings and thus becomes even more under dense (over dense). Thus Equation (43) is the fundamental equation of non-stationary disc accretion. Stability analysis can be made based on these equations. We shall look for solutions to Equations (41) and (43) of the form which represents the perturbations considering short wavelength modes of the form,
 (45)
(45)
where 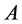 is a constant,
is a constant, 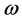 the angular frequency and k the wave number and
the angular frequency and k the wave number and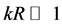 . For such modes, variations in disc quantities can be ignored over a wavelength and
. For such modes, variations in disc quantities can be ignored over a wavelength and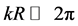 . Viscous instability then follows when
. Viscous instability then follows when 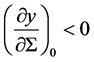 with y being influenced by the magnetic field. Since the magnetic diffusivity is fixed then we drop subscribe zero and the shear part of the magnetic stress from Equation (44) and we obtain the same as Equation (43)
with y being influenced by the magnetic field. Since the magnetic diffusivity is fixed then we drop subscribe zero and the shear part of the magnetic stress from Equation (44) and we obtain the same as Equation (43)
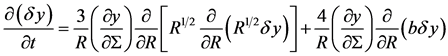 (46)
(46)
Substitution of Equation (45) into (46) gives an expression for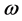 . The viscous diffusion term dominates the magnetic term in Equation (46) in determining
. The viscous diffusion term dominates the magnetic term in Equation (46) in determining , since it contains a term in
, since it contains a term in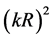 , while the magnetic term is only linear in
, while the magnetic term is only linear in . It follows that the sign of
. It follows that the sign of  determines the sign of
determines the sign of 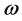 and hence the stability of the perturbation. The magnetic field affects the viscous stability by influencing the form of
and hence the stability of the perturbation. The magnetic field affects the viscous stability by influencing the form of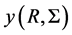 . The increase in
. The increase in ![]() due to the effect of the magnetic field. The magnetic field generated due to internal dynamo is dominant in our model (Paper I & II) as a result the disc is stable in the presence of strong magnetic field in the gas pressure dominated disc. Because the magnetic field due to the internal dynamo may maintain sufficient angular momentum transport throughout in such type of disc. But in the radiation pressure dominated disc the toroidal magnetic field generated by an internal dynamo is independent of dynamical viscosity as well as the magnetic field is weak compared to the gas pressure dominated disc (Paper II), then the innermost disc region is unstable.
due to the effect of the magnetic field. The magnetic field generated due to internal dynamo is dominant in our model (Paper I & II) as a result the disc is stable in the presence of strong magnetic field in the gas pressure dominated disc. Because the magnetic field due to the internal dynamo may maintain sufficient angular momentum transport throughout in such type of disc. But in the radiation pressure dominated disc the toroidal magnetic field generated by an internal dynamo is independent of dynamical viscosity as well as the magnetic field is weak compared to the gas pressure dominated disc (Paper II), then the innermost disc region is unstable.
From the perturbation equations we can find a dispersion relation, which will give solutions that are stable and unstable in addition to the stability condition which have already used above. Substituting Equation (45) into (4) we have
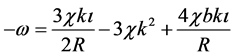 (47)
(47)
where,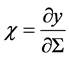 .
.
Equation (47) is the general dispersion relation and will help us to investigate the stability of our disc model. From the right hand side equation the first and the second term in Equation (47) is due to viscous stress, which is the first and the second orders of k the leading term in k is the quadratic term, the third terms are due to magnetic field generated by the internal dynamo. For the short wavelength limit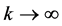 , Equation (47) gives,
, Equation (47) gives,
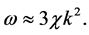 (48)
(48)
When real part of the solution![]() , then it satisfies the stability condition and from the real part
, then it satisfies the stability condition and from the real part ![]() then the disc is unstable (Figure 1). Weakly magnetised accretion discs are subject to a powerful axisymmetric instability. Strongly magnetized accretion discs are subjected to stability conditions.
then the disc is unstable (Figure 1). Weakly magnetised accretion discs are subject to a powerful axisymmetric instability. Strongly magnetized accretion discs are subjected to stability conditions.
The dispersion relation (48) indicates that the most rapidly growing wave numbers in a thin disc have growing rates. The growing rate is dependent on the strength of the magnetic field. For imaginary of 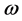 the instability criterion is most easily satisfied than the real part of it but the azimuthal component of the strong magnetic field (dynamo field) tends to stabilize. Generally the dispersion relation is used to investigate the stability properties of the accretion disc by considering the local perturbation of the disc as shown in Figure 1.
the instability criterion is most easily satisfied than the real part of it but the azimuthal component of the strong magnetic field (dynamo field) tends to stabilize. Generally the dispersion relation is used to investigate the stability properties of the accretion disc by considering the local perturbation of the disc as shown in Figure 1.
4. Discussions
4.1. Timescales and Stability
The time-dependent accretion discs with a-parameter viscosity were constructed by [2] and its flow is controlled by the size of the viscosity. Hence observations of time-dependent disc behaviour offer one of the few sources of quantitative information, it is important to consider the relative magnitudes of the various timescales over which accretion discs form and evolve and the effect of magnetic field is observed on timescales. We begin by identifying the typical timescales on which the disc structure may vary.
The dynamical time scale 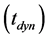 is simply related as:
is simply related as:
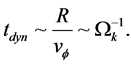 (49)
(49)
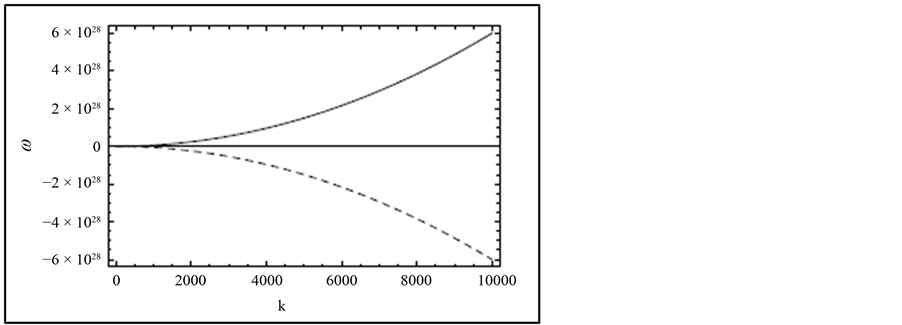
Figure 1. The graph of dispersion relation for ω in radian/s versus wave number k in m−1 which shows stability and instability of the disc. Solid line indicates positive value of ω for large values of k (stable region) and dashed line indicates negative value of ω for large values of k (unstable region).
This is the shortest time scale present in the disc, which is the Keplerian period, that ranges very small in the inner region and increases to outer disc and also the typical growth time of some important instabilities, such as the magneto-rotational instability. Using steady state equation we can write this as
![]() s(50)
s(50)
![]() (51)
(51)
We see that the dynamical timescale depends on mass of the accretor, accretion rate, magnetic moment and radius and also measures the speed with which hydrostatic equilibrium in the vertical direction is established. From Equations (50) and (51) the dynamical time scale increases when the magnetic field is strong.
Thermal time scale 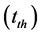 which is responsible for readjustment to thermal equilibrium and mathematically given by
which is responsible for readjustment to thermal equilibrium and mathematically given by
 (52)
(52)
We thus see that 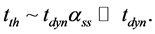
Viscous time scale (tvisc): a time in which angular momentum distribution changes due to torque caused by dissipative stresses. The viscous timescale sets the scale for the evolution of the surface density. From the analysis of time dependent models above, we have seen that this timescale is given by the viscous time scale
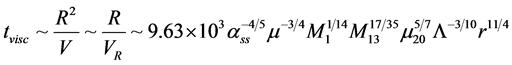 (53)
(53)
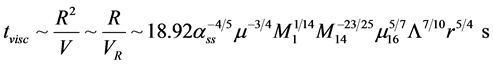 (54)
(54)
which gives the timescale on which matter diffuses through the disc under the effect of viscous torques. The viscosity has the effect of spreading the original ring in radius on a typical time scale, assuming that the typical length scale for surface density gradients in the disc is . This is an order of magnitude longer than other time scales. Using the
. This is an order of magnitude longer than other time scales. Using the 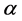 -parameterization we can also write
-parameterization we can also write
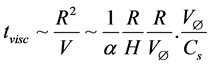
The viscous and the dynamical time scales can be related as
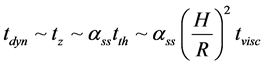 (55)
(55)
Then from Equation (55) the thermal time scale is
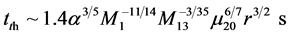 (56)
(56)
 (57)
(57)
The thermal time scale is large in the region of weak magnetic field or inner region of the disc (see Equations (56) and (57)) which leads to instability of the disc. Since α < 1 then the three time scales can be related by a well-defined hierarchy of timescales
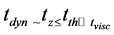
As long as the disc is thin, we thus see that the various timescales are ordered in the following way:
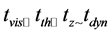 (58)
(58)
which then shows that the centrifugal balance in the radial direction and hydrostatic balance in the vertical direction are very rapidly achieved, while the disc temperature generally evolves on a longer timescale, and finally, on an even longer timescale, one can see some evolution in the surface density profile.
Finally, note that all of the above timescales are a function of radius. In particular, if H/R are constant which is not our case (which is not generally true), then they all scale in the same way, and for a Keplerian disc, they increase with radius as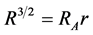 . Thus the evolution of the inner disc is generally much more rapid than the evolution of the outer disc. Suppose now that a small perturbation is made to a generally considered equilibrium solution and that this perturbation continues to grow rather than being damped. Then the supposed steady solution is said to be unstable and cannot occur in reality. The sharp difference we have found in the various timescales means we can distinguish different types of instability. If for example the energy balance is distributed in the disc, any instability will grow on a timescale tth, which is much less than tvisc. Since tvisc is the timescale for different changes in the surface density
. Thus the evolution of the inner disc is generally much more rapid than the evolution of the outer disc. Suppose now that a small perturbation is made to a generally considered equilibrium solution and that this perturbation continues to grow rather than being damped. Then the supposed steady solution is said to be unstable and cannot occur in reality. The sharp difference we have found in the various timescales means we can distinguish different types of instability. If for example the energy balance is distributed in the disc, any instability will grow on a timescale tth, which is much less than tvisc. Since tvisc is the timescale for different changes in the surface density  to occur, we can assume that
to occur, we can assume that 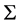 is fixed during the growth time tth. We refer to this as a thermal instability. For α < 1 we also have tth >
is fixed during the growth time tth. We refer to this as a thermal instability. For α < 1 we also have tth > ![]() − tz, so the vertical structure of the disc can respond rapidly, on a timescale tz, to changes due to the thermal instability, and keep the vertical structure close to hydrostatic equilibrium.
− tz, so the vertical structure of the disc can respond rapidly, on a timescale tz, to changes due to the thermal instability, and keep the vertical structure close to hydrostatic equilibrium.
4.2. Stability Analysis
In Paper I & II we calculated the solution of 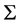 numerically by writing the relations in the form
numerically by writing the relations in the form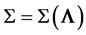 . To investigate the viscous stability of the solution we calculate the derivatives of
. To investigate the viscous stability of the solution we calculate the derivatives of 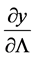 using the results of the Paper I & II for a slightly perturbed value of
using the results of the Paper I & II for a slightly perturbed value of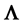 . When this derivative is positive the solution is viscously stable, otherwise it is viscously unstable.
. When this derivative is positive the solution is viscously stable, otherwise it is viscously unstable.
Equation (39) gives the viscosity integral 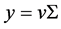 for given
for given ,
, ![]() and other parameters as a function of r. In more general situation when the system is time-dependent, there is no fixed
and other parameters as a function of r. In more general situation when the system is time-dependent, there is no fixed 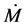 but in our work we use accretion rate in steady state, and time-independent equation has to be replaced by an explicitly time-dependent diffusion type equation for
but in our work we use accretion rate in steady state, and time-independent equation has to be replaced by an explicitly time-dependent diffusion type equation for . In any case, in order to close the system of equations we need another equation that relates 𝚲 with
. In any case, in order to close the system of equations we need another equation that relates 𝚲 with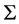 . In the time-dependent case the sign of
. In the time-dependent case the sign of 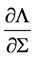 determines whether the solution is viscously stable (positive sign) or unstable (negative sign). In paper I Equations (39) and (40) we have the relations
determines whether the solution is viscously stable (positive sign) or unstable (negative sign). In paper I Equations (39) and (40) we have the relations , R = rRA, use of these relations in Equation (44) and dropping the subscript zero and the shear component of the magnetic stress with similar reason given in Section 5.4 we obtain
, R = rRA, use of these relations in Equation (44) and dropping the subscript zero and the shear component of the magnetic stress with similar reason given in Section 5.4 we obtain
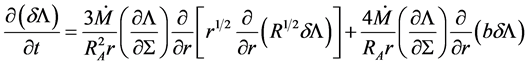 (59)
(59)
In the gas pressure dominated disc when the accretion rate increases the magnetic field due to dynamo increases (strong field is generated) as result sufficient angular momentum is transported which lead to stability of the disc properties. But in the radiation pressure dominated disc the inner edge of accretion disc close to the surface of the neutron star and the magnetic field due to dynamo decrease which cannot shut off the instability. From paper I Equation (47) 𝚲 and 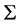 were related by Equation (60).
were related by Equation (60).
From the dispersion relation Equation (60) gives information for stability and instability of disc with positive and negative slope. Figure 2 shows that positive and negative slope indicate stability and instability of the disc. This is basically comes from the time-dependent equation of accretion disc around magnetized stars.
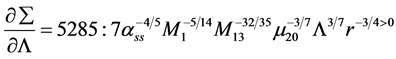 (60)
(60)
this is the case for steady-disc which shows the disc is stable.
For the time-dependent disc we have
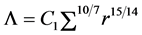 (61)
(61)
where

and hence
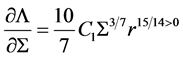 (62)
(62)
which gives that

In this case steady disc flow is possible and which satisfies stability condition. Therefore, steady state model is stables against small perturbation in the gas pressure and free-free absorption dominated disc (that is positive slope). Since in the gas pressure dominated disc the magnetic field is strong than the radiation pressure dominated disc, the strong magnetic field generated by internal dynamo helps the disc to be stable. We can also show stability of the disc using the derivatives of temperature with respect to the surface density as shown in Figure 3
 (63)
(63)
the disc is stable. When , and a viscous instability, this time known as the Lightman-Eardley instability. The time-dependent discs give us information to explain the torque reversal of X-ray pulsars by reversing the
, and a viscous instability, this time known as the Lightman-Eardley instability. The time-dependent discs give us information to explain the torque reversal of X-ray pulsars by reversing the
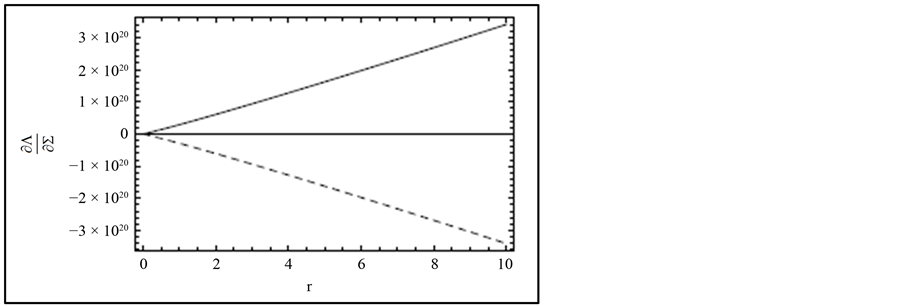
Figure 2. 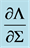 (dimensionless) as a function of r = R/RA = radius ratio for the gas pressure dominated region. The solid and dashed lines show stability and instability of the disc, respectively.
(dimensionless) as a function of r = R/RA = radius ratio for the gas pressure dominated region. The solid and dashed lines show stability and instability of the disc, respectively.
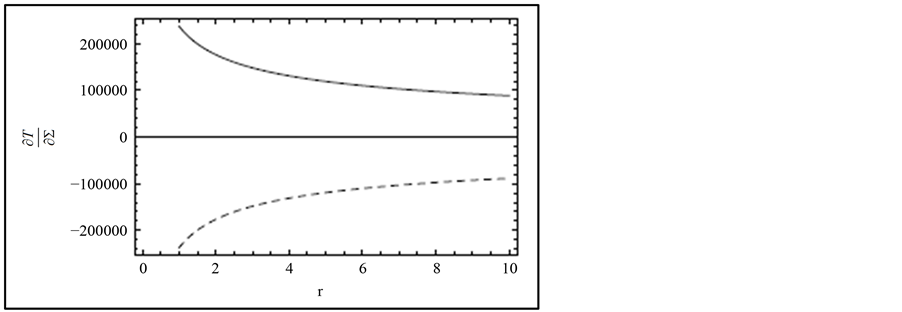
Figure 3. 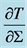 (in K) as a function of r = R/RA, radius ratio for the gas pressure dominated region. The solid and dashed lines show stability and instability of the disc, respectively.
(in K) as a function of r = R/RA, radius ratio for the gas pressure dominated region. The solid and dashed lines show stability and instability of the disc, respectively.
magnetic field in the disc with similar magnitude of spin-up and spin down torques which depends on the inner and corotation radii. In linearly stable disc we can observe the stable torques, and it is non-linearly unstable because otherwise no torque reversal would occur. Since in the star disc interacting system presence of a disc dynamo produces a significant enhancement of the torque between the magnetic field of the neutron star and the accretion disc.
In this case steady disc flow is possible and which satisfies stability condition. Therefore, steady state model is stable against small perturbation in the gas pressure and free-free absorption dominated disc.
In the inner regions of the disc where the radiation pressure and an electron scattering opacity is dominant, then 𝚲 (dimensionless) and 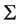 (in kg∙m−2) are related as (see Paper II Equation (52))
(in kg∙m−2) are related as (see Paper II Equation (52))
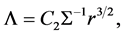 (64)
(64)
where,
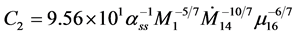 .
.
Thus
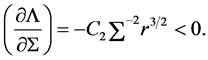
which is the condition for viscous instability (negative slope).
5. Conclusions
We have studied the stability of thin, axisymmetric accretion disc with an internal dynamo around magnetised stars in order to do a linear stability analysis of our steady disc solutions supported by an internal dynamo using time-dependent equations. This gives us the tool to start exploring the stability properties of the disc. Perturbation of the surface density and dynamo-component of the magnetic field and the general dispersion relation tell us stability properties of our disc. The disc is unstable to the surface density and thermal perturbation in the local approximation when the radiation pressure becomes dominant as seen in Equation (64). Our finding shows that the time scale varies within the magnetic field, in the inner regions of the disc the thermal time scale is large compared to outer regions of the disc because the magnetic field is weak. Thus the inner most disc region is unstable (see Figure 4) and the outer and the middle regions are stable.
In the presence of strong magnetic field the disc is stable, while for weak magnetic field the instability develops. In our model the presence of magnetic field generated due to internal dynamo plays a great role for the stability of the disc. As we have seen from Figure 1 to Figure 4 the stability and instability of the disc depend on the wavelength (dispersion relation), the nature of the magnetic field and the regions of the disc that is gas pressure and radiation pressure dominant part.
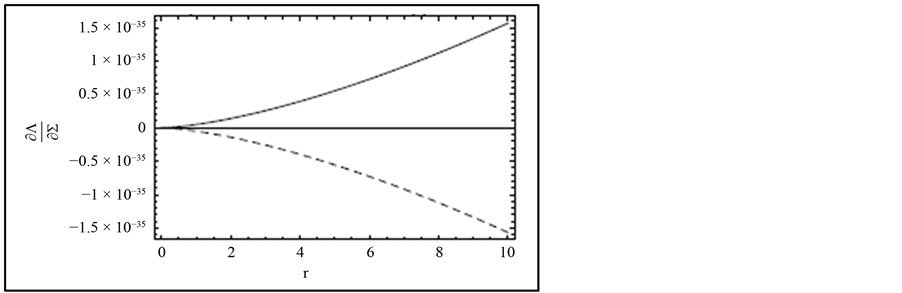
Figure 4. 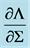 (dimensionless) as a function of r = R/RA= radius ratio for the inner region (radiation pressure dominated) disc. The solid and dashed lines show stability and instability of the disc, respectively.
(dimensionless) as a function of r = R/RA= radius ratio for the inner region (radiation pressure dominated) disc. The solid and dashed lines show stability and instability of the disc, respectively.
Acknowledgements
This research has made use of NASA’s Astrophysics Data System.
References
- Shakura, N.I. and Sunyaev, R.A. (1973) Black Holes in Binary Systems. Observational Appearance, 24, 337-355.
- Lightman, A.P. and Eardley, D.M. (1974) Black Holes in Binary Systems: Instability of Disc Accretion. Astrophysical Journal, 187, L1-L3. http://dx.doi.org/10.1086/181377
- Pringle, J.E., Rees, M.J. and Pacholczyk, A.G. (1973) Accretion onto Massive Black Holes. Astronomy & Astrophysics (A&A), 29, 179-184.
- Shakura, N.I. and Sunyaev, R.A. (1976) Theory of the Instability of Disc Accretion onto Black Holes and the Variability of Binary X-Ray Sources, Galactic Nuclei and Quasars. MNRAS, 175, 613-632.
- Kato, S. (1978) Pulsational Instability of Accretion Disks to Axially Symmtric Oscillations. MNRAS, 185, 629-642.
- Bluenthal, G.R., Lin, D.N.C. and Yang, L.T. (1984) Astrophysical Journal, 287, 7743.
- Balbus, S.A. and Hawley, J.F. (1991) A Powerful Local Shear Instability in Weakly Magnetized Discs. I. Linear Analysis. Astrophysical Journal, 376, 214-222. http://dx.doi.org/10.1086/170270
- Stone, et al. (1996) MNRAS, 175, 613.
- Tout, C.A. and Pringle, J.E. (1992) Accretion Disc Viscosity: A Simple Model for a Magnetic Dynamo. MNRAS, 259, 604-612.
- Tessema, S.B. and Torkelsson, U. (2010) The Structure of Thin Accretion Discs around Magnetised Stars. Astronomy & Astrophysics (A&A), 509.
- Tessema, S.B. and Torkelsson, U. (2011) Thin Accretion Discs around Millisecond Pulsars. MNRAS, 412, 1650-1658. http://dx.doi.org/10.1111/j.1365-2966.2010.18002.x
- Ghosh, P. and Lamb, F.K. (1979) Accretion by Rotating Magnetic Neutron Stars. II Radial and Vertical Structure of the Transition Zone in Disc Accretion. Astrophysical Journal, 232, 259-276. http://dx.doi.org/10.1086/157285
- Ghosh, P. and Lamb, F.K. (1979) Accretion by Rotating Magnetic Neutron Stars. III. Accretion Torques and Period Changes in Pulsating X-Ray Sources. Astrophysical Journal, 234, 296-316. http://dx.doi.org/10.1086/157498
- Hawley, J.F., Gammie, C.F. and Balbus, S.A. (1995) Local Three-Dimensional MHD Simulation of Accretion Discs. Astrophysical Journal, 440, 742. http://dx.doi.org/10.1086/175311
- Brandenburg, A., Nordlund, A.A., Stein, R.F. and Torkelsson, U. (1995) Dynamo-Generated Turbulence and Large Scale Magnetic Fields in a Keplerian-Shear Flow. Astrophysical Journal, 446, 741-754. http://dx.doi.org/10.1086/175831
- Torkelsson, U. (1998) Astrophysical Journal, 463, 656.

