International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36180,7 pages DOI:10.4236/ijaa.2013.33024
What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2013 Mohamed S. El Naschie. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 1, 2013; revised July 5, 2013; accepted July 13, 2013
Keywords: Kaluza-Klein Dark Energy; Quantum Particle as Zero Set; Quantum Wave as an Empty Set; Quantum Gravity Experiments; Hawking-Hartle Wave; Dark Energy of the Quantum Wave; Scaling the Planck Scale; Equivalence of Einstein-Rosen Bridges; Spooky Action at Distance
ABSTRACT
We reason that in quantum cosmology there are two kinds of energy. The first is the ordinary energy of the quantum particle which we can measure. The second is the dark energy of the quantum wave by quantum duality. Because measurement collapses the Hawking-Hartle quantum wave of the cosmos, dark energy cannot be detected or measured in any conventional manner. The quantitative results are confirmed using some exact solutions for the hydrogen atom. In particular the ordinary energy of the quantum particle is given by  where
where 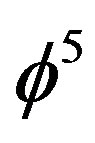 is Hardy’s probability of quantum entanglement,
is Hardy’s probability of quantum entanglement, 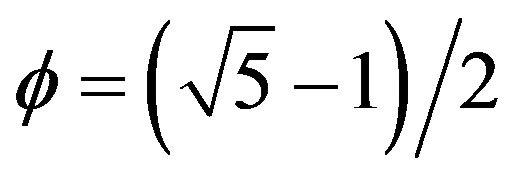 is the Hausdorff dimension of the zero measure thin Cantor set modeling the quantum particle, while the dark energy of the quantum wave is given by E(D) = (5
is the Hausdorff dimension of the zero measure thin Cantor set modeling the quantum particle, while the dark energy of the quantum wave is given by E(D) = (5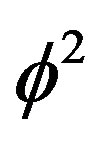 /2)(mc2) where
/2)(mc2) where 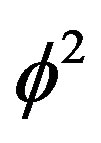 is the Hausdorff dimension of the positive measure thick empty Cantor set modeling the quantum wave and the factor five (5) is the Kaluza-Klein spacetime dimension to which the measure zero thin Cantor set
is the Hausdorff dimension of the positive measure thick empty Cantor set modeling the quantum wave and the factor five (5) is the Kaluza-Klein spacetime dimension to which the measure zero thin Cantor set  and the thick empty set
and the thick empty set  must be lifted to give the five dimensional analogue sets namely
must be lifted to give the five dimensional analogue sets namely  and
and 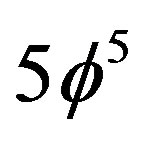 needed for calculating the energy density
needed for calculating the energy density 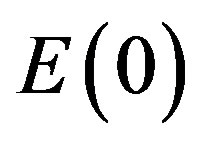 and
and 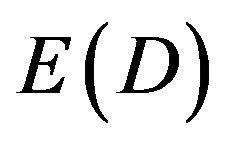 which together add to Einstein’s maximal total energy density
which together add to Einstein’s maximal total energy density 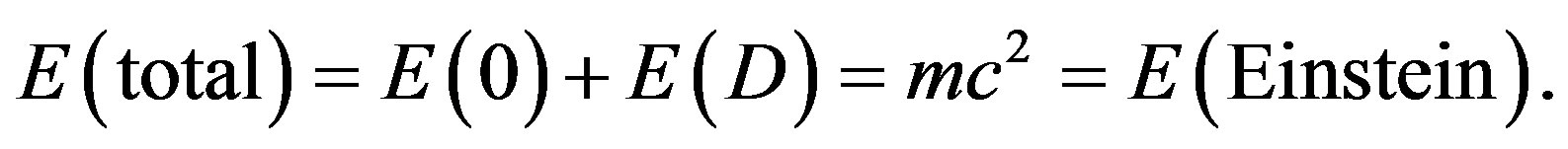 These results seem to be in complete agreement with the WMAP, supernova and recent Planck cosmic measurement as well as the 2005 quantum gravity experiments of V. V. Nesvizhersky and his associates. It also confirms the equivalence of wormhole solutions of Einstein’s equations and quantum entanglement by scaling the Planck scale.
These results seem to be in complete agreement with the WMAP, supernova and recent Planck cosmic measurement as well as the 2005 quantum gravity experiments of V. V. Nesvizhersky and his associates. It also confirms the equivalence of wormhole solutions of Einstein’s equations and quantum entanglement by scaling the Planck scale.
1. Introduction
We will not and cannot be as brief as Salvador Dali when he was asked to give a talk but to religiously mind the time. Dali went to the podium and said “I will be brief; in fact I have finished my talk” and returned to his seat. Nevertheless knowing how precious space in a scientific journal is, the author will be reasonably brief.
Dark energy is the energy of the Hawking-Hartle quantum wave of the universe. This wave is the solution of the Wheeler-DeWitt equation of the cosmos which is essentially a Schrödinger equation for the entire universe. Since measurement leads to a state vector reduction i.e. quantum wave collapse, dark energy could not possibly be detected at least not using the current measurement technologies and all what we can measure is the ordinary energy of the particle side of the wave-particle duality of the quantum world. Now that we have been really brief, we better start explaining things in a little bit more detail.
2. Background Information
Take a line segment representing a unit interval, which in turn represents a one dimensional “spacetime”. We start by randomly removing parts of this line except for the end points, in a manner reminiscent of what we do when we construct a deterministic middle third Cantor set but adding randomness to the iteration [1,2]. In the case of the classical Cantor set we end up, after infinitely many iterations, with a Hausdorff dimension amounting to 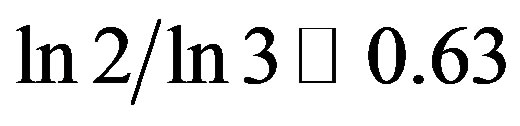 describing a measure zero set [1-4]. Noting that we have nothing left except uncountably many Cantorian points of topological dimension equal zero [1-4], a dimension equal 0.63 is relatively speaking quite substantial [2-4]. For the random Cantor set at hand, the situation is quite similar but instead of
describing a measure zero set [1-4]. Noting that we have nothing left except uncountably many Cantorian points of topological dimension equal zero [1-4], a dimension equal 0.63 is relatively speaking quite substantial [2-4]. For the random Cantor set at hand, the situation is quite similar but instead of  as a Hausdorff dimension we end up with the remarkable golden mean value
as a Hausdorff dimension we end up with the remarkable golden mean value 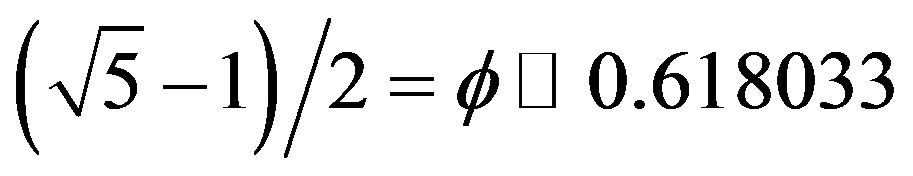 as was shown some time ago by American Mathematicians, Mauldin and Williams [5-7]. Considering now that for the original line segment both the topological and the Hausdorff dimensions coincide and are equal to
as was shown some time ago by American Mathematicians, Mauldin and Williams [5-7]. Considering now that for the original line segment both the topological and the Hausdorff dimensions coincide and are equal to 
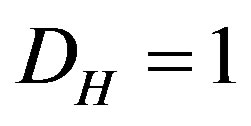 , then it follows that for the gaps left representing, by definition and construction, regions of no space and no time, we have a Hausdorff dimension equal to
, then it follows that for the gaps left representing, by definition and construction, regions of no space and no time, we have a Hausdorff dimension equal to 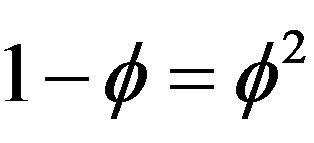 [3-6]. To summarize the above thus far we have two things (see Figures 1 and 2):
[3-6]. To summarize the above thus far we have two things (see Figures 1 and 2):
a) An uncountable infinite number of zero dimensional points with zero measure [2,7] i.e. zero length and a points set possessing a Hausdorff dimension equal to f [3-7]. In nonlinear dynamics such a set is called a thin Cantor set and is used in our theory to model the quantum particle;
b) An infinite but countable number of gaps with a

Figure 1. Transfinite set theoretical formulation of particle-wave duality of quantum physics.

Figure 2. Quantum entanglement, measurement and the energy of the quantum wave.
complementary Hausdorff dimension equal to 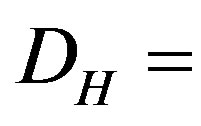
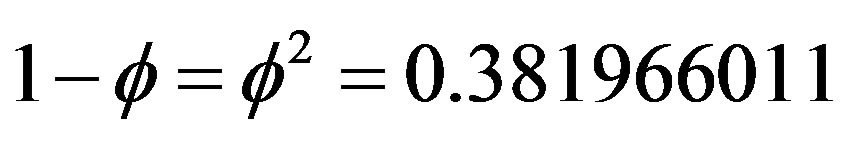 [8-11]. By contrast the measure i.e. the length of the complementary set is still equal to 1 – 0 = 1. Unlike (a) this set is called a fat or “thick” Cantor set which is relevant to KAM theorem [6] and is used in our theory to model the quantum wave or even spacetime itself which could be one and the same thing.
[8-11]. By contrast the measure i.e. the length of the complementary set is still equal to 1 – 0 = 1. Unlike (a) this set is called a fat or “thick” Cantor set which is relevant to KAM theorem [6] and is used in our theory to model the quantum wave or even spacetime itself which could be one and the same thing.
3. Analysis
Our next step is to lift both the 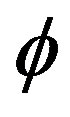 points representing thin Cantor set and the
points representing thin Cantor set and the  collection of gaps representing a fat “fractal” Cantor set to Kaluza-Klein five dimensional spacetime [12,13]. Proceeding in this way we encounter again two distinct situations (see Figures 1 and 2):
collection of gaps representing a fat “fractal” Cantor set to Kaluza-Klein five dimensional spacetime [12,13]. Proceeding in this way we encounter again two distinct situations (see Figures 1 and 2):
i) For 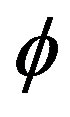 we calculate a quasi-Hausdorff hyper area [8-11] by extending our familiar multiplicative area and volume definition to formally five dimensions. That means
we calculate a quasi-Hausdorff hyper area [8-11] by extending our familiar multiplicative area and volume definition to formally five dimensions. That means 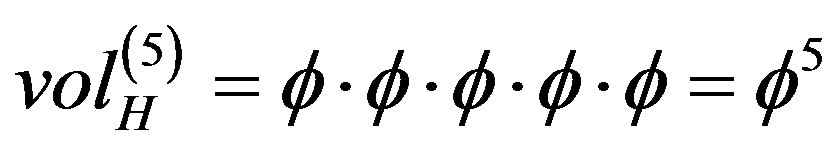 for a Kaluza-Klein
for a Kaluza-Klein  spacetime [12,13]. We note parenthetically that
spacetime [12,13]. We note parenthetically that 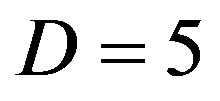 in our case is not motivated by D = 4 Einstein spacetime plus D = 1 for electromagnetism-gravity unification. It is motivated rather by the fact that we have five fundamental interactions, namely magnetic, electric, strongweak force and gravity [8]. Since the topological probability of finding a “Cantor point” in our set is
in our case is not motivated by D = 4 Einstein spacetime plus D = 1 for electromagnetism-gravity unification. It is motivated rather by the fact that we have five fundamental interactions, namely magnetic, electric, strongweak force and gravity [8]. Since the topological probability of finding a “Cantor point” in our set is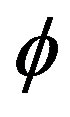 , then
, then 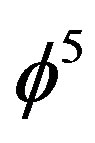 can be understood as an application of the intersection rule of sets or alternatively as the multiplication theorem of probabilistic events [2,6-8]. The so obtained set is essentially a five dimensional zero set or quantum particle;
can be understood as an application of the intersection rule of sets or alternatively as the multiplication theorem of probabilistic events [2,6-8]. The so obtained set is essentially a five dimensional zero set or quantum particle;
ii) For 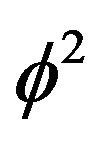 on the other hand, we have a hyper circumference of the area and thus a dual additive quasiHausdorff measure representing the total length of the circumference of a pentagon with the length of each side being equal to
on the other hand, we have a hyper circumference of the area and thus a dual additive quasiHausdorff measure representing the total length of the circumference of a pentagon with the length of each side being equal to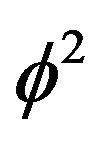 . In other words lifting additively the Hausdorff dimension of the complementary set i.e.
. In other words lifting additively the Hausdorff dimension of the complementary set i.e. 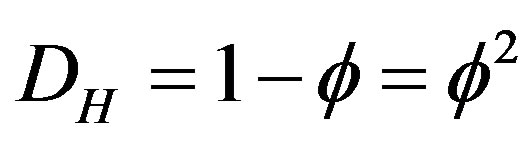 to D = 5 would give us a quasi-hyper surface
to D = 5 would give us a quasi-hyper surface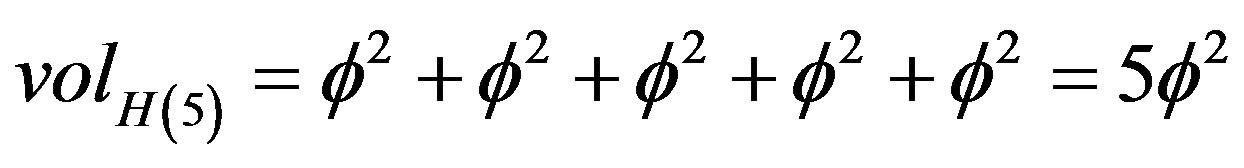 . Similar to
. Similar to , the result may be interpreted as the application of the addition rule of events of probability theory or equivalently as the union rule of sets [2,6-8]. The so obtained set is a five dimensional empty set or a quantum wave. In fact it could be regarded as a D = 5 quantum spacetime.
, the result may be interpreted as the application of the addition rule of events of probability theory or equivalently as the union rule of sets [2,6-8]. The so obtained set is a five dimensional empty set or a quantum wave. In fact it could be regarded as a D = 5 quantum spacetime.
Next we look at the magnitude of Newtonian kinetic energy 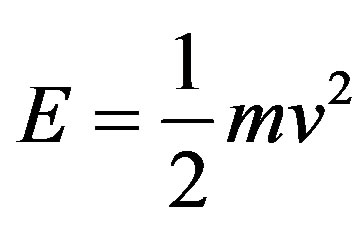 stored inside
stored inside 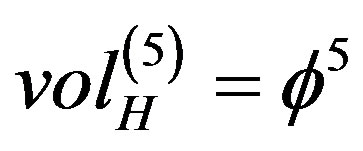 and
and
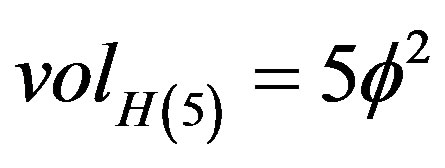 when
when 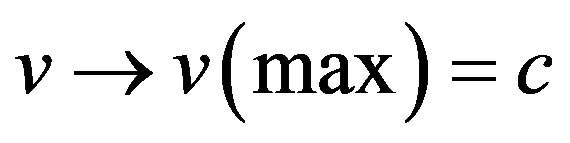 where m is mass, v is velocity and c is the multi-fractal expectation value of the speed of light [8,14]. In a similar manner to the above, we find two different types of energies (as summarized in Figures 1 and 2):
where m is mass, v is velocity and c is the multi-fractal expectation value of the speed of light [8,14]. In a similar manner to the above, we find two different types of energies (as summarized in Figures 1 and 2):
1) The energy associated with the density 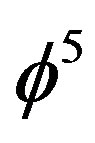 is obviously
is obviously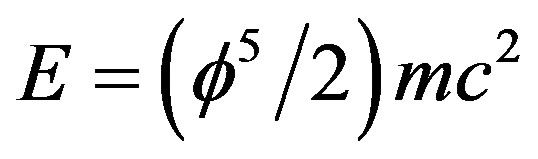 . Noting that
. Noting that 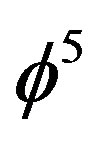 is equal to the celebrated Hardy probability for quantum entanglement [8,15] where
is equal to the celebrated Hardy probability for quantum entanglement [8,15] where 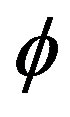 is the Hausdorff dimension for the zero set fractal (i.e. a set of only zero in it) modeling the quantum particle given by
is the Hausdorff dimension for the zero set fractal (i.e. a set of only zero in it) modeling the quantum particle given by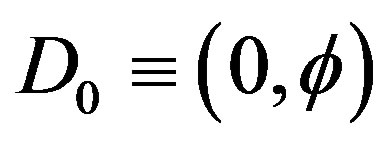 , then we see that this is the ordinary energy of a quantum particle or the quantum position or potential energy which will be denoted by
, then we see that this is the ordinary energy of a quantum particle or the quantum position or potential energy which will be denoted by  [14]. This energy density is only 4.5% of what Einstein’s relativity theory predicts classically and is thus equal to the energy density found from the WMAP and Planck measurement and that concluded from supernova cosmological data analysis of the accelerated rate of expansion of the universe [14,16-19]. In fact this is a quantum gravity formula which is indirectly confirmed experimentally in the work of V.V. Nesvizhevsky et al. [20]. This excellent work casts the darkest shadow on the equivalence principle;
[14]. This energy density is only 4.5% of what Einstein’s relativity theory predicts classically and is thus equal to the energy density found from the WMAP and Planck measurement and that concluded from supernova cosmological data analysis of the accelerated rate of expansion of the universe [14,16-19]. In fact this is a quantum gravity formula which is indirectly confirmed experimentally in the work of V.V. Nesvizhevsky et al. [20]. This excellent work casts the darkest shadow on the equivalence principle;
2) By contrast for the energy due to the density 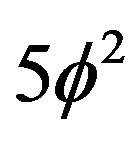 associated with pentagonal surface or halo of the D = 5 particle connected to a set with nothing in it, i.e. the empty set
associated with pentagonal surface or halo of the D = 5 particle connected to a set with nothing in it, i.e. the empty set 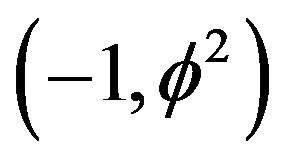 by which classical set theory starts, or the quantum wave in D = 5, we have
by which classical set theory starts, or the quantum wave in D = 5, we have  [5]. Relative to the potential energy of the particle and remembering that a quantum particle has no classical path, the energy represents something resembling the quantum kinetic energy of the ‘ghost’ wave propagation [8]. It is easily shown that this is the value of the supposedly missing dark energy of the cosmos [14,16,17] and will therefore be denoted by
[5]. Relative to the potential energy of the particle and remembering that a quantum particle has no classical path, the energy represents something resembling the quantum kinetic energy of the ‘ghost’ wave propagation [8]. It is easily shown that this is the value of the supposedly missing dark energy of the cosmos [14,16,17] and will therefore be denoted by
 .
.
This energy obviously has a different sign to  and produces therefore a form of negative pressure or antigravity force [17] which explains the increased rate of cosmic expansion observed in relatively recent accurate cosmological measurements [17] and we attribute it to the negative Cartan-Cosserat type of torsional anticlastic curvature [19,21] of the compactified 22 bosonic dimensions of spacetime as distinct from the normal 4 large dimensions [8], (i.e. 3 space and one time dimension fused together relativistically). It is similar to Hawking’s negative vacuum fluctuation at a black hole horizon [8].
and produces therefore a form of negative pressure or antigravity force [17] which explains the increased rate of cosmic expansion observed in relatively recent accurate cosmological measurements [17] and we attribute it to the negative Cartan-Cosserat type of torsional anticlastic curvature [19,21] of the compactified 22 bosonic dimensions of spacetime as distinct from the normal 4 large dimensions [8], (i.e. 3 space and one time dimension fused together relativistically). It is similar to Hawking’s negative vacuum fluctuation at a black hole horizon [8].
4. Einstein Total Energy and Quantum Wave-Particle Duality
From the above we must conclude that when summing up  and
and 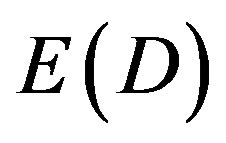 we must obtain E(Einstein) total potential energy density which is easily verified using elementary arithmetic based on the fact that
we must obtain E(Einstein) total potential energy density which is easily verified using elementary arithmetic based on the fact that 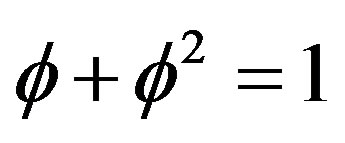 and
and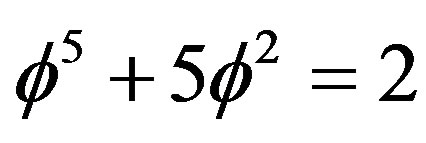 . Thus we have the wonder which is no wonder namely that
. Thus we have the wonder which is no wonder namely that
 (1)
(1)
One of our most important final conclusions is thus the following:
Dark energy is the absolute value of the negative energy of the quantum surface or the outside of the quantum particle i.e. the quantum wave which we cannot detect because of state vector reduction while ordinary energy is the energy of the inside core of the quantum wave which is the quantum particle and which we can measure. In set theoretical terminology [5], ordinary energy is the energy of the zero set while dark energy is the complementary energy of the empty set [18,19]. An equivalent string theoretical explanation leading to the same conclusion is to consider dark energy to be due to the anticlastic curvature caused by the 22 compactified dimensions of the 26 dimensions of bosonic strings’ spacetime theory as just mentioned earlier on.
Einstein’s energy is consequently blind to any distinction between dark energy and ordinary energy density. However our measurement apparatus which collapses the wave feels the difference and can register only ordinary energy and that is the explanation for the result of the cosmological measurement, be it that only 4.5% of the energy predicted by the Theory of Relativity [17] is present as far as our measurement instruments are concerned or that the universe is pushed apart rather than being pulled together as we previously presumed and which new accurate measurements have now contradicted [14,16,17].
5. Mathematical Consistency and Theoretical Physics
We note that because the axiomatic structure of set theory and mathematical consistency could not be guaranteed without the introduction of the empty set as well as the zero set, then by the same token it follows that fundamental quantum physics and quantum gravity could not be consistent nor deeply understood except by embracing the vital role of the particle-wave duality and its connection to the zero set-empty set duality. In a nutshell traditional physics does not recognize the empty set and equate it to an absolute nothingness. It is imperative to recognize that physics depends upon logical structure and it should never confuse the zero set with the empty set. It is equally imperative not to confuse either the zero set or the empty set with insubstantial total nothingness [5,19]. We may also note here that as there is an infinite hierarchy of infinites, there is a corresponding infinite hierarchy of empty sets [19] which forms the quantum wave and for cosmic scales forms quantum spacetime itself [8,21].
6. The Hawking-Hartle Quantum Wave of the Universe
In our opinion, our by far most important conclusion is with regard to what we have already hinted to above namely the fact that our measurement instruments cannot detect any dark energy. The reason is surprisingly obvious and straight forward. The entire universe is described by the Wheeler-DeWitt version of the Schrödinger equation [8]. Therefore the solution of this equation namely the Hawking-Hartle quantum wave function of the universe [8] must collapse on cosmic measurement. Consequently dark energy cannot be measured unless we can develop highly sophisticated nondemolition quantum collapse free measurement instruments [16,17]. However, we may have here an extremely subtle point, namely that the Hawking-Hartle wave is not simply a quantum wave but it is the entire quantum spacetime of our existence. This could mean that we do not have three things, namely particle, wave and spacetime background but possibly only two things, namely either particle and wave without background or particle and wavy fractal spacetime.
7. Discussion, the Hydrogen Atom and Conclusion
One should not be entirely surprised that an empty set has a physical effect because a quantum wave is conventionally regarded as merely a probability wave, devoid of ordinary matter or energy, also has a physical effect. It is an elementary fact of quantum physics discovered long ago by Max Born that the square of the probability wave function gives the probability of finding the spatial location of a quantum particle [6]. In a way dark energy discloses the mystery of the quantum wave function and vice versa. That may be a circulatory explanation or worst still tautology. However logical understanding is partially achieved by reducing the number of concepts. At a minimum this is what we have done here. To prove this point even more force fully we just need to mention how our 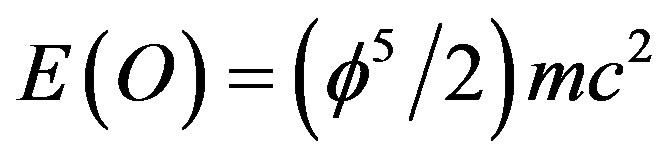 may be obtained from “running” the exact solution of the hydrogen atom energy ground state
may be obtained from “running” the exact solution of the hydrogen atom energy ground state 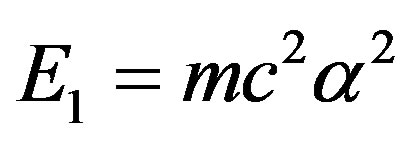 as a function of the energy by varying the electromagnetic fine structure constant and transforming
as a function of the energy by varying the electromagnetic fine structure constant and transforming 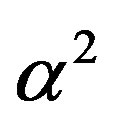 to
to 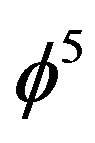 as explained in detail in Chart 1 [22]. Thus the missing 95.5% dark energy of the cosmos is nothing but the kinetic quantum energy of the Hawking-Hartle quantum wave of the universe which collapses upon measurement preventing the direct detection of this negative energy is behind the negative pressure causing the increased acceleration of the measured rate of cosmic expansion at the edges of the universe. We stress that the partial revision of E = mc2 to E(0) = mc2/22 and E(D)
as explained in detail in Chart 1 [22]. Thus the missing 95.5% dark energy of the cosmos is nothing but the kinetic quantum energy of the Hawking-Hartle quantum wave of the universe which collapses upon measurement preventing the direct detection of this negative energy is behind the negative pressure causing the increased acceleration of the measured rate of cosmic expansion at the edges of the universe. We stress that the partial revision of E = mc2 to E(0) = mc2/22 and E(D) 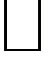 mc2(21/22) does not contradict any experiment nor of course cosmic measurements [16,17]. In fact the semi classical COW experiments as well as the recent first experimental observations of gravitational quanta [20] indirectly confirm our theoretical results and cast the strongest doubt on the equivalence principle [23] as merely an excellent semi-classical approximation which is incompatible with quantum mechanics [21]. In order to be able to obtain the same results consistent with the cosmic observations from the equations of relativity we must at least use a more sophisticated geometry than Einstein’s 4D flat or Rieman nian geometry [8]. We could, for instance, start from Witten-Duff maximally symmetric manifold with 528 states and realize that these 528 states in eleven
mc2(21/22) does not contradict any experiment nor of course cosmic measurements [16,17]. In fact the semi classical COW experiments as well as the recent first experimental observations of gravitational quanta [20] indirectly confirm our theoretical results and cast the strongest doubt on the equivalence principle [23] as merely an excellent semi-classical approximation which is incompatible with quantum mechanics [21]. In order to be able to obtain the same results consistent with the cosmic observations from the equations of relativity we must at least use a more sophisticated geometry than Einstein’s 4D flat or Rieman nian geometry [8]. We could, for instance, start from Witten-Duff maximally symmetric manifold with 528 states and realize that these 528 states in eleven

Chart 1. Cosmic quantum relativity energy of the quantum particle E(O) = (ϕ5/2)(mc2) from the exactly solvable classical model of the hydrogen atom.
dimensions include the 504 states of Heterotic superstrings in ten dimensions [8]. This leads to a division into 528 − 504 = 24 isometries related to curvature and ordinary energy and 504 related to anticlastic curvature, anti-gravity and dark energy [21]. Consequently we have two parameters  for ordinary energy and
for ordinary energy and  for dark energy in full agreement with our present theory and results as well as our previous calculations [18,19,21]. In fact by regarding Hardy’s quantum entanglement P(H) =
for dark energy in full agreement with our present theory and results as well as our previous calculations [18,19,21]. In fact by regarding Hardy’s quantum entanglement P(H) = 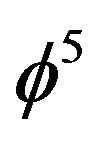 as the topological Planck energy it follows that 1/
as the topological Planck energy it follows that 1/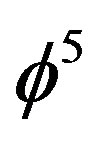 = 11 +
= 11 + 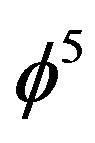 is the topological Planck length and thus by scaling the Planck scale in this manner, we demonstrated the equivalence among wormholes, i.e. Einstein-Rosen bridges and quantum entanglement as well as dark energy and Hawking’s negative vacuum fluctuation at the edge of black hole horizon and the negative dark energy at the edge of the universe.
is the topological Planck length and thus by scaling the Planck scale in this manner, we demonstrated the equivalence among wormholes, i.e. Einstein-Rosen bridges and quantum entanglement as well as dark energy and Hawking’s negative vacuum fluctuation at the edge of black hole horizon and the negative dark energy at the edge of the universe.
REFERENCES
- B. Mandelbrot, “The Fractal Geometry of Nature,” Freeman, New York, 1983.
- F. Morgan, “Geometric Measure Theory,” Elsevier, Amsterdam, 2009.
- A. Stakhov, “The Mathematics of Harmony,” World Scientific, New Jersey, 2009.
- M. S. El Naschie, O. E. Rossler and I. Prigogine, “Quantum Mechanics, Diffusion and Chaotic Fractals,” Pergamon Press, Elsevier, Oxford, 1995.
- J. Huan-He and M. S. El Naschie, “On the Monadic Nature of Quantum Gravity as Highly Structured Golden Ring Spaces and Spectra,” Fractal Spacetime & NonCommutative Geometry in Quantum & High Energy Physics, Vol. 2, No. 2, 2012, pp. 94-98.
- M. S. El Naschie, “A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 19, No. 1, 2004, pp. 209-236. doi:10.1016/S0960-0779(03)00278-9
- M. S. El Naschie, “The Theory of Cantorian Spacetime and High Energy Particle Physics. (An Informal Review),” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2635-2646. doi:10.1016/j.chaos.2008.09.059
- R. Penrose, “The Road to Reality,” Jonathan Cape, London, 2004.
- H. Coxeter, “The Beauty of Geometry,” Dover Publications, New York, 1999.
- H. Coxeter, “Regular Polytops,” Dover Publication, New York, 1973.
- I. Bengtsson and K. Zyczkowski, “Geometry of Quantum States,” Cambridge University Press, Cambridge, 2006. doi:10.1017/CBO9780511535048
- P. Halpern, “The Great Beyond, Higher Dimensions, Parallel Universes and the Extraordinary Search for a Theory of Everything,” John Wiley, New Jersey, 2004.
- M. S. El Naschie, “Kaluza-Klein Unification—Some Possible Extensions,” Chaos, Solitons & Fractals, Vol. 37, No. 1, 2008, pp. 16-22. doi:10.1016/j.chaos.2007.09.079
- M. S. El Naschie and L. Marek-Crnjac, “Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity,” International Journal of Modern Nonlinear Theory and Application, Vol. 1, No. 4, 2012, pp. 118-124. doi:10.4236/ijmnta.2012.14018
- M. S. El Naschie, “Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry,” Journal of Quantum Information Science, Vol. 1, No. 2, 2011, pp. 50-53. doi:10.4236/jqis.2011.12007
- L. Amendola and S. Tsujikawa, “Dark Energy Theory and Observations,” Cambridge University Press, Cambridge, 2010.
- E. J. Copeland, M. Sami and S. Tsujikawa, “Dynamics of Dark Energy,” arxiv:hep-th/0603057V3, 2006.
- M. S. El Naschie, “A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory,” Journal of Quantum Information Science, Vol. 3, No. 1, 2013, pp. 23-26. doi:10.4236/jqis.2013.31006
- L. Marek-Crnjac, M. S. El Naschie and J.-H. He, “Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 1A, 2013, pp. 78-88. doi:10.4236/ijmnta.2013.21A010
- V. V. Nesvizhevsky, “Study of Neutron Quantum States in Gravity Field,” The European Physical Journal, Vol. C40, 2005, p. 479. doi:10.1140/epjc/s2005-02135-y
- M. S. El Naschie, “Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave,” Journal of Modern Physics, Vol. 4, No. 5, 2013, pp. 591-596. doi:10.4236/jmp.2013.45084
- M. R. Pahlavani, “Relativistic Schrödinger Wave Equation for Hydrogen Atom Using Factorization Method,” Open Journal of Microphysics, Vol. 3, No. 1, 2013, pp. 1-7. doi:10.4236/ojm.2013.31001
- S. Clark, “Differently Equal,” New Scientist, Vol. 219, No. 2925, 2013, pp. 33-36. doi:10.1016/S0262-4079(13)61751-0

