International Journal of Astronomy and Astrophysics
Vol. 3 No. 2 (2013) , Article ID: 32345 , 6 pages DOI:10.4236/ijaa.2013.32008
Distances Scale Determination for a Planetary Nebula in Galactic Bulge
1Department of Astronomy and Space, Baghdad University, Baghdad, Iraq
2Department of Physics, Baghdad University, Baghdad, Iraq
3Minstery of Electricity, Baghdad, Iraq
Email: Sundusalbakri70@yahoo.com
Copyright © 2013 Sundus A. Abdullah et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 5, 2013; revised February 6, 2013; accepted February 15, 2013
Keywords: Planetary Nebulae; Masses; Distances Planetary Nebulae
ABSTRACT
Planetary Nebulae (PN) distances represent the fundamental parameter for the determination the physical properties of the central star of PN. In this paper the distances scale to Planetary Nebulae in the Galactic bulge were calculated related to previous distances scales. The proposed distance scale was done by recalibrated the previous distance scale technique CKS/D82. This scale limited for nearby PN (D ≤ 3.5 kpc), so the surface fluxes less than other distance scales. With these criteria the results showed that the proposed distance scale is more accurate than other scales related to the observations for adopted sample of PN distances, also the limit of ionized radius (Rio) for all both optically thick and optically thin in the rang of sizes (0.45 > Rio (pc) > 0.03).
1. Introduction
There are several methods available to determine individual distances, independent of any assumptions concerning the information on the properties of the Nebula. These distances give independent information on the properties, of the nebula, especially mass and density for the nebulae [1,2].
By making certain assumptions on the nebular structure, distances can be calculated by measurement of fluxes, angular sizes, and electron densities. These methods called statistical distances [3]. As well determined distance scale for Planetary Nebulae (PN) is necessary for the investigation of the space density, galactic distribution, total number of PN, and the birth rate of PN in the galaxy [2,4].
2. Previous Distances Scales
The previous statistical distances rely on Planetary Nebulae sharing certain common physical properties and the previous distances are derived from the measurement of two or more nebular parameters [1]. A number of theoretical mass-radius relationships have been constructed based on the H-burning tracks of Schonberner and Blocker (BS90) and various models of nebular expansion as Zhang and Kwok (1993) and Mellema (1994) [5,6].
During the last decade several such distance scales have been proposed, notably Cahn et al. (1992) (here after CKS), Van de Steen and Zijlstra (1995) (VdSZ), Zhang (1995) (Z95), Schneides and Buckley (SB96), and Stanghelline and Shaw with Villaver (2008) (SSV). The previous scales which will be indicated in this work as the following:
Daub in 1982 used an empirically relation between the ionized masses of Planetary Nebulae and a particular function of observational quantities was used to calculate the distances to the samples of Planetary Nebulae. These distances are used to investigate the scale height of the galactic distribution of Planetary Nebulae (125 pc), the rate of formation of Planetary Nebulae (5 ± 2 × 10–3 PN kpc–3·yr–1). The effective ionized mass (µ) define as [4]
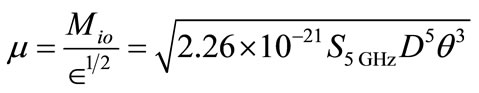 (1)
(1)
where Mio: is the ionized mass of PN in Sun mass unit (solar mass);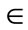 : is the filling factor used to allow for the non spherical geometry of the nebula
: is the filling factor used to allow for the non spherical geometry of the nebula
θ: is the angular diameter in arcs unit
S5 GHz: is the radio flux at 5 GHz in W·m–2·Hz–1 unit, or called Janskys (Jy) unit where Jy = 10–26 W·m–2·Hz–1;
D: is the distance in parsec unit (pc).
The optical thickness parameter, T is given by [2]
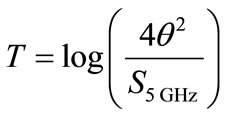 (2)
(2)
Daub plotted the quantity of Equation (1) (logµ) against the quantity of Equation (2) optical thickness (log T) as shown in Figure 1, from the relations obtained by a least-squares analysis, the equations of the two mean lines, the effective ionized mass and optical thickness are given by the following relations [2,4]:
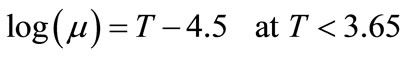 (3)
(3)
 (4)
(4)
1) For optically thick PN
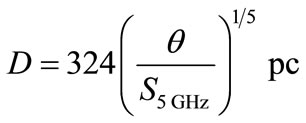 (5)
(5)
2) For optically thin PN
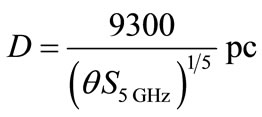 (6)
(6)
Cahn recalibrated the Daub’s distance scale by using samples of 19 Planetary Nebulae with well observed distances [2], as shown in Figure 2. The fit to the distance scale
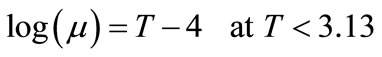 (7)
(7)
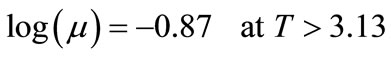 (8)
(8)
The calculated distances by CKS scale were split in two types [2,6].
1) For optically thick PN
 (9)
(9)
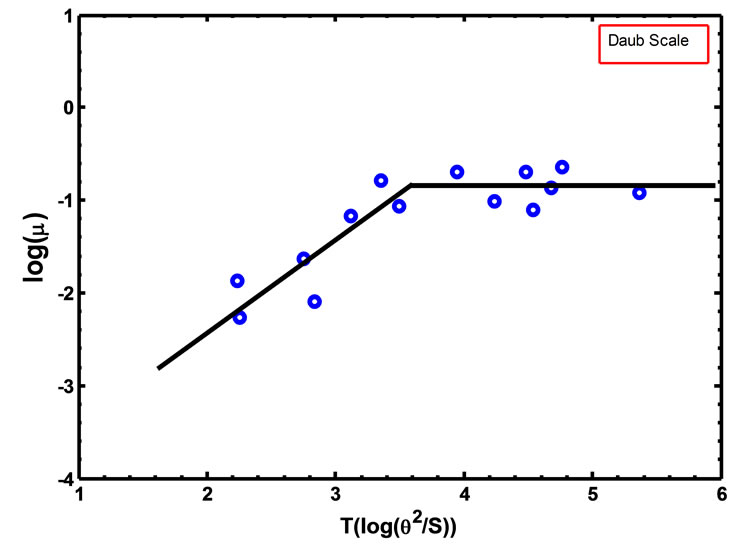
Figure 1. The relation between ionized mass and the optical thickness according to Daub scale (D82).
2) For optically thin PN
 (10)
(10)
For the distance determination CKS used radio fluxes and optical diameters except for nebulae with very small angular sizes, where radio diameters obtained with Vela Large Array (VLA) were used [6]. Stanghellini et al. calculated the distances for PN by re-calibrated the distance scale of CKS using the nebular parameters relative to the LMC and SMC PN observed by Hubble Space Telescope (HST), as shown in Figure 3 [7].
The fit lines of distances scale which were found by SSV scale based on the Magellanic Clouds PN are
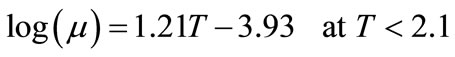 (11)
(11)
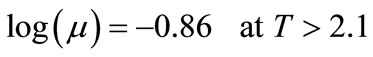 (12)
(12)
This method based on transformation between 5 GHz and Hβ flux [8]. SSV scale calculated the distances for the samples of PN, by using the following equations [2]:
1) For optically thick PN
 (13)
(13)
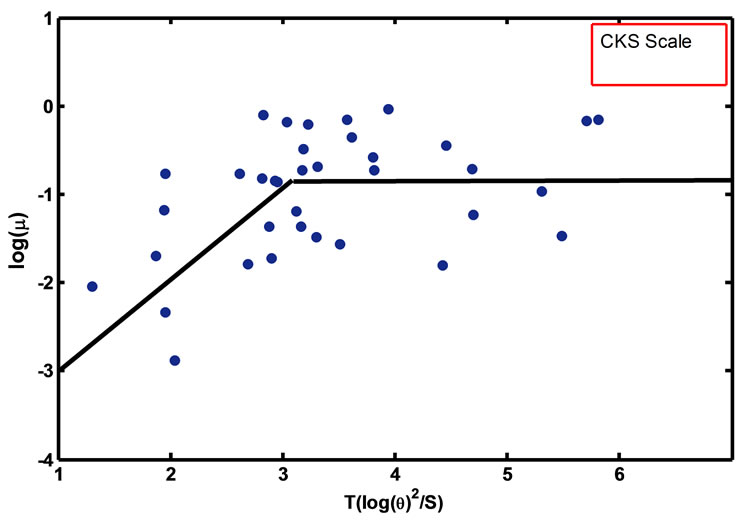
Figure 2. The relation between ionized mass and the optical thickness according to CKS scale.
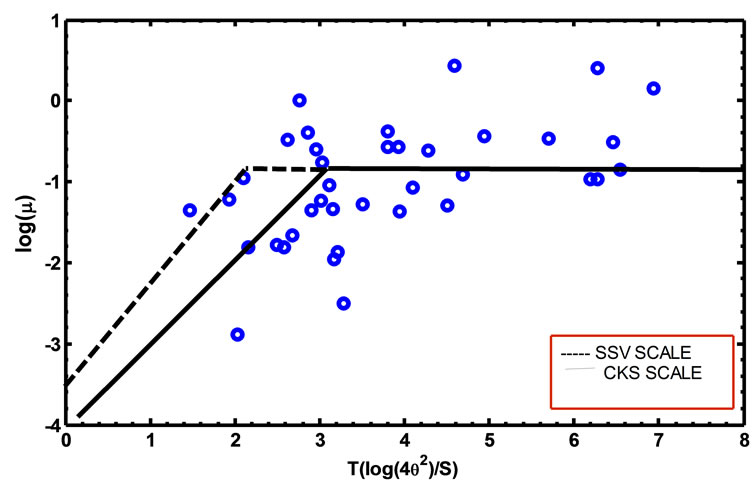
Figure 3. The relation between ionized mass and the optical thickness, SSV distance comparing with CKS distance.
2) For optically thin PN
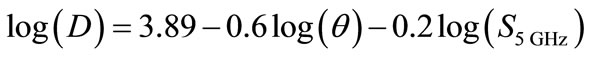 (14)
(14)
Using the similar technique we recalibrate the Cahn and Kaller(CK)/Daub distance for the sample of planetary nebulae using the resolved companion central star to determined their distances, a new scale have been found to determine the distance for the a sample of PN in Galactic Bulge as tabulated in Table 1.
3. Proposed Distance Scale (Syth10)
This method based on the results of Hubble Space Telescope (HST) survey of Galactic Planetary Nebulae (GPN), designed to detect and measure resolved binary PN companions.
The sample of PN in our Scale was chosen using criteria designed to maximize our chances of finding resolved companion stars. First among these criteria was that objects in our choosing had to be nearby. Nearly all of our selections have statistical distances from Cahn, Kaller (1990) (CKS); Zhang (1995) (Z95); Stanghellini and Shaw and Villaver (2008) (SSV) that are less than ~3.5 kpc.
Second criteria that the Galactic latitude for PN were chosen to have |b| > 10˚. A third selection criteria was known of the binarity of the central stars.
Computational Method for the Proposed Scale (Syth10)
The proposed scale in this work were done by recalibrated CKS/D82 scale and used the Equation (1) to find the effective ionized mass and then plot versus optical thickness as shown in Figure 4, the fit to the ionized masses as the following equations:
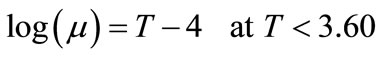 (15)
(15)
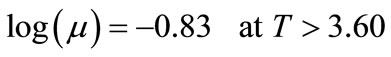 (16)
(16)
The programming results and figures were performed by using Matlab package.
Distances obtained by proposed scale performed by plot the observed distances values versus optical thickness which were given by Table 1, then fit to the distance scale by the following equations:
1) For optically thick PN
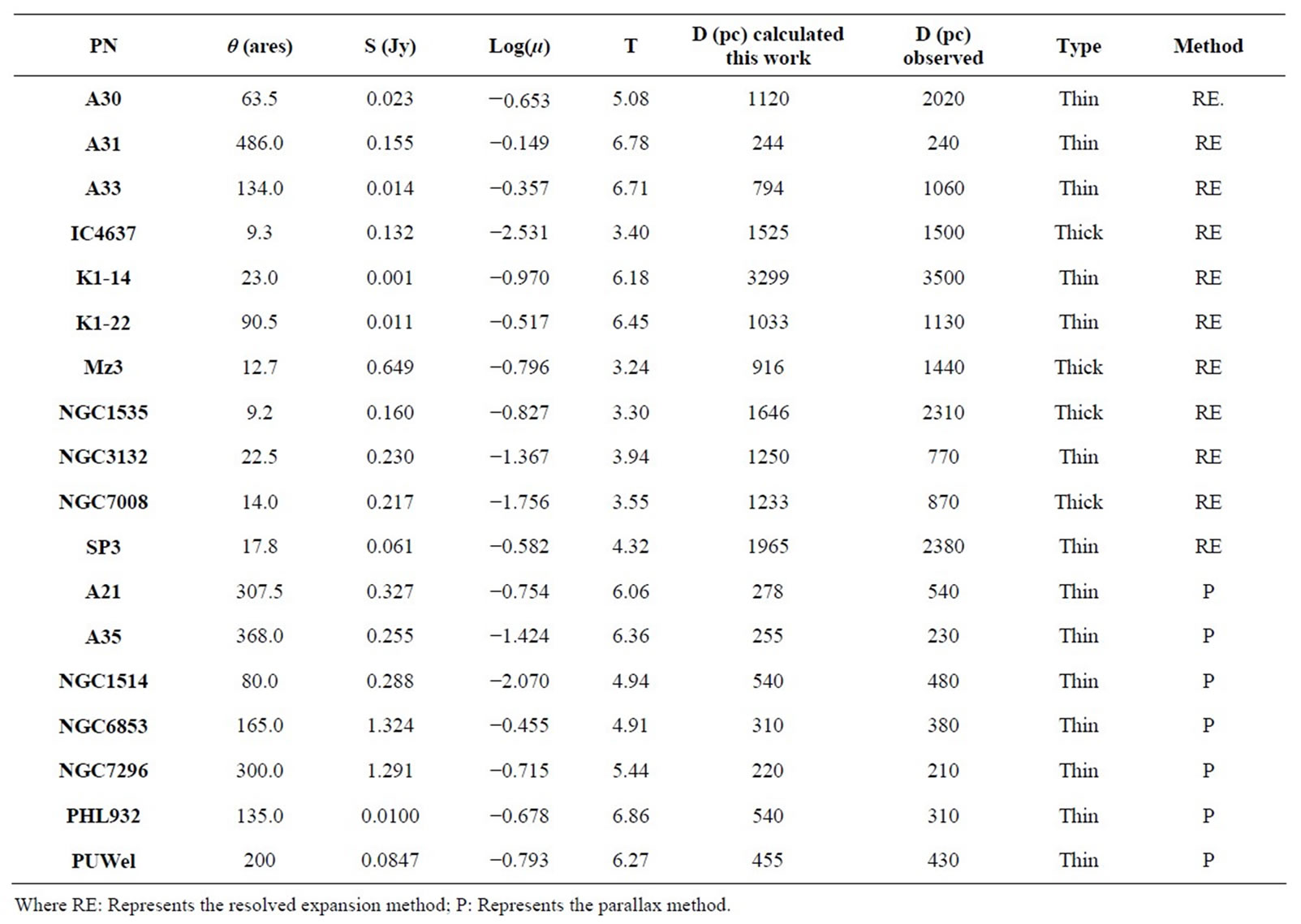
Table 1. Represent the values of angular sizes with the optical thicknesses for the samples of PN. The observed and calculated distances are estimated.

Figure 4. The relation between ionized mass and the optical thickness, the individual nebulae listed in Table 1. This work distance scale.
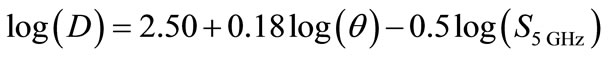 (17)
(17)
Planetary Nebulae (PN) display a positive correlation between the ionized mass and the size. On very general ground that Planetary Nebulae during the first evolutionary stages is optically thick to Lyman continuum radiation, and its ionized mass is considerably smaller than the total mass. As the objects expand and become optically thin the ionized mass also increases, approaching value of the total mass. The whole process suggests that the ionized mass increases proportionally to the radius of the Planetary Nebulae. The simplest form of such a relation is a linear one, which we have established using our data for closing PN. The least squares straight line is
 (18)
(18)
where a = 1.225 and b = –0.0123. This equation can be considered a first order approximation to the masses of the Planetary Nebulae, as compared to the zeroth—order constant mass of Shklovisky’s method [9,10]. Our limit of Rio for all both optically thick and optically thin in a rang of sizes is given by
 (19)
(19)
These limits are comparing with the previous limits in Pottasch (1992), which is given by [10]
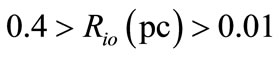 (20)
(20)
and with the limits of the resents observations which is given by [2]
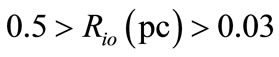 (21)
(21)
4. Discussions and Conclusions
The distance was derived by Daub for the optically thin nebulae (log4θ2/S5 GHZ > 3.65) if an available flux is at 5 GHz, an adjustments of that to frequency = 5 GHz. For optically thick the distance derived (logθ2/S5 GHZ < 3.65), it is possible that some of the most expanded PN become optically thick for a second time as their central stars contract to near White Dwarf (WD).
From Figure 1, it is apparent that most PN are likely to have ionized masses smaller than optically thin PN. This scale (D82) depends on the calibration of few samples PN in Galactic Bulge.
CKS improved D82’s calibration with the use large number of calibrator’s, and he calculated the distances to 778 galactic PN [2]. The scale’s distance of calibration was shown in Figure 2.
As a result, the previous distance scales that seem to work well with samples, for example those in Galactic Bulge or External Galaxies, may not be applicable to more divers population of local Planetary Nebulae. The values of (θ) and surface brightness were given in the catalogues of CKS and SSV for the samples which were adopted [2,8].
From these scales we estimated the number of nebulae that are optically thick and optically thin according to the previous scales which were indicated, as shown in Figures 5 to 8. Specifically adopted sample tend to have lower surface brightness than the traditional calibration objects. This difference may arise from a selection effect:
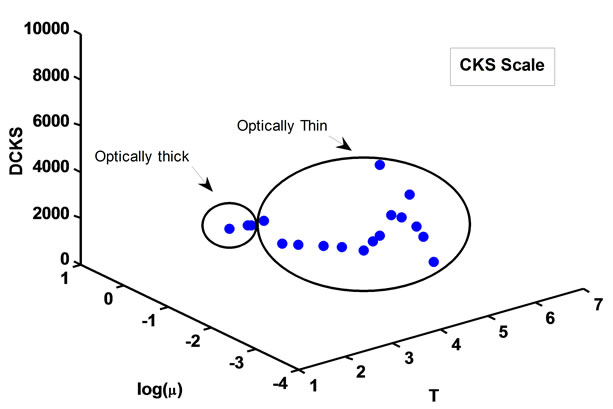
Figure 5. The relation between distance (DCKS) and optical thickness with the ionized mass, three nebulas represent optically thick.
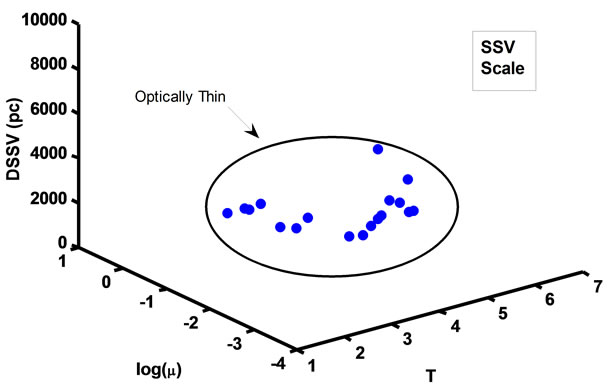
Figure 6. The relation between distance (DSSV) and optical thickness with the ionized mass, all nebulas represent optically thick.
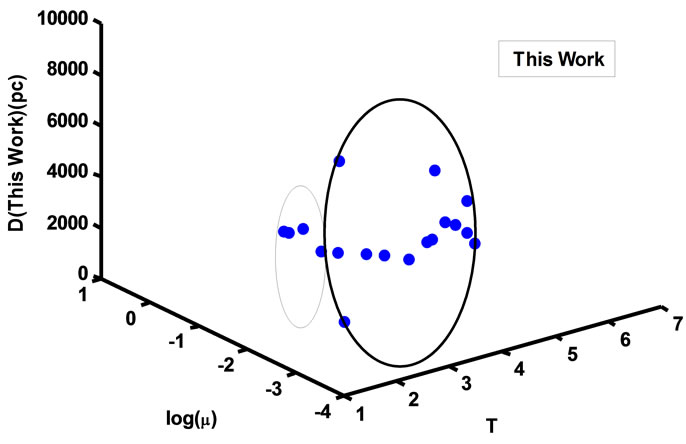
Figure 7. The relation between distance (this work) and optical thickness with the ionized mass, four nebulae represent optically thick.
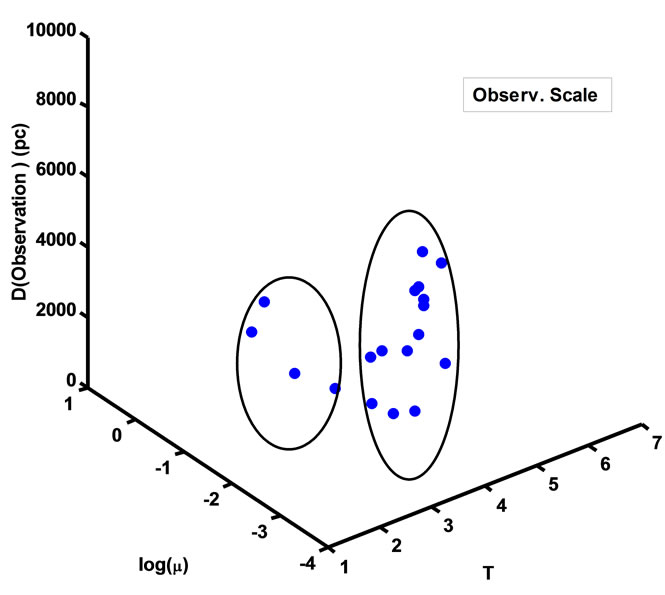
Figure 8. The relation between distance and optical thickness with the ionized mass, four nebulae represent optically thick.
PN in our survey are typically nearby, old nebulae, whereas most of the objects that calibrate statistical techniques are low-latitude, high surface brightness, and more distant nebulae.
Comparison of our proposed distances with those obtained from most various distances scales shows that all of the latter have systematically overestimated the distances by factors ranging up to factor of 2. The various distances were plotted versus angular expansion; the best fitting equations were obtained as
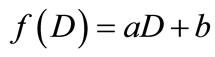 (22)
(22)
where a and b represent the coefficients of fitting equations. The comparison of our scales with the different previous scales was illustrated by plotting the distances with versus best fitting equations (f(D)) as shown in Figures 9 and 10. The results estimated the accurate scale and demonstrated the fitting lines for the CKS and SSV with the scale of this work in compare with the observation distance. We show these errors most likely due to

Figure 9. Comparison the proposed scales distance with the different previous distances, all lines represents fitting lines.
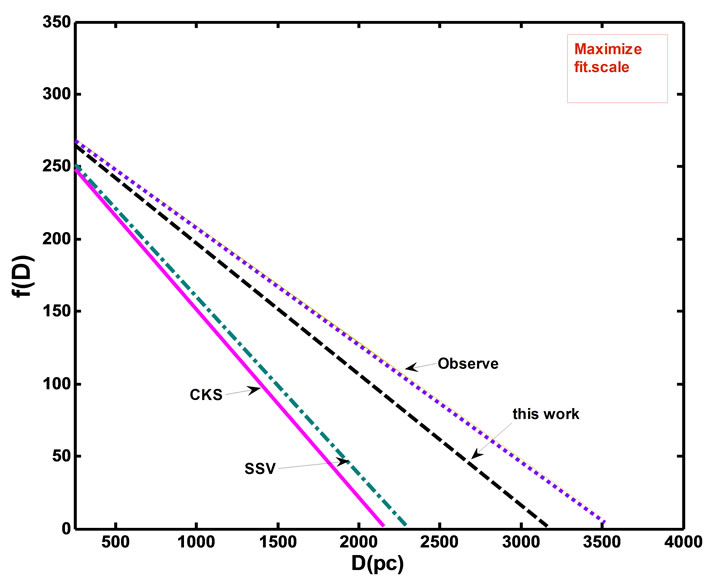
Figure 10. Represents maximized for fitting lines distance scale according to four distances scale. Our scale appear more approaching to the observing distance than other scales.
the fact that the properties of our Planetary Nebulae with binary nuclei are systematically different from those of PN used to calibrate statistical methods.
5. Acknowledgements
It is pleasure to thank Dr. S. Kwok in Hong Kong University, China, for his many critical comments on earlier drafts of his manuscript, and for Dr. B.T. Chiad in Baghdad University, whose comments have also led to improvements of the paper.
REFERENCES
- G. Lizett, G. Yolanda and L. Loinard, “Distance Estimated Based on Angular Expansion for the Planetary Nebulae NGC6881,” Astronomy Journal, Vol. 2, 2011, pp. 1-5.
- S. Lizia, S. Richard and V. Eva, “The Magellanic Cloud Calibration of the Galactic Planetary Nebulae Distance Scale,” Astrophysical Journal, Vol. 80, 2008, pp. 1129- 1150.
- S. Kwok, “The Origin and Evolution of Planetary Nebulae,” 2nd Edition, Cambridge University Press, New York, 2001.
- G. Daub, “Statistical Surveys of Local Planetary Nebulae,” Astrophysical Journal, Vol. 260, 1982, pp. 612-624.
- J. Kaller and J. Lutiz, “Dust-distances to Planetary Nebulae ,” Publication of the Astronomical Society of the Pacific (PASP), Vol. 97, 1985, pp. 700-706. doi:10.1086/131593
- T. Bensby and L. Lunstrom, “The Distance Scale of Planetary Nebulae,” Astronomy and Astrophysics Journal, Vol. 374, No. 2, 2001, pp. 599-614. doi:10.1051/0004-6361:20010705
- R. Shaw and L. Stanghellini, “Hubble Space Telescope Images of the Magellanic Cloud Planetary Nebulae,” Astrophysical Journal, Vol. 167, 2006, p. 201.
- J. Cahn and J. Kaller, “A Catalogues of Absolute Fluxes and Distances of Planetary Nebulae,” Astronomy and Astrophysics Journal, Vol. 94, 1992, pp. 399-410.
- S. Pottasch, “Local Space Density and Formation Rate of Planetary Nebulae,” Astronomy and Astrophysics Journal, Vol. 307, 1996, pp. 561-573.
- S. Pottasch, “Shklovsky Distance to Galactic Bulge Planetary Nebulae,” Astronomy and Astrophysics Journal, Vol. 256, 1992, pp. 251-257.

