International Journal of Astronomy and Astrophysics
Vol.1 No.3(2011), Article ID:7358,8 pages DOI:10.4236/ijaa.2011.13016
The Precise Inner Solutions of Gravity Field Equations of Hollow and Solid Spheres and the Theorem of Singularity
Institute of Innovative Physics in Fuzhou, Department of Physics, Fuzhou University, Fuzhou, China
E-mail: ycwlyjs@yeah.net
Received May 26, 2011; revised June 28, 2011; accepted July 12, 2011
Keywords: General Relativity, Inner Solutions of Hollow and Solid Spheres, Black Hole, Theorem of Singularity
Abstract
The precise inner solutions of gravity field equations of hollow and solid spheres are calculated in this paper. To avoid space curvature infinite at the center of solid sphere, we set an integral constant to be zero directly at present. However, according to the theory of differential equation, the integral constant should be determined by the known boundary conditions of spherical surface, in stead of the metric at the spherical center. By considering that fact that the volumes of three dimensional hollow and solid spheres in curved space are different from that in flat space, the integral constants are proved to be nonzero. The results indicate that no matter what the masses and densities of hollow sphere and solid sphere are, there exist space-time singularities at the centers of hollow sphere and solid spheres. Meanwhile, the intensity of pressure at the center point of solid sphere can not be infinite. That is to say, the material can not collapse towards the center of so-called black hole. At the center and its neighboring region of solid sphere, pressure intensities become negative values. There may be a region for hollow sphere in which pressure intensities may become negative values too. The common hollow and solid spheres in daily live can not have such impenetrable characteristics. The results only indicate that the singularity black holes predicated by general relativity are caused by the descriptive method of curved space-time actually. If black holes exist really in the universe, they can only be the Newtonian black holes, not the Einstein’s black holes. The results revealed in the paper are consistent with the Hawking theorem of singularity actually. They can be considered as the practical examples of the theorem.
1. Introduction
We know that the static solutions of the Einstein’s equation of gravity field with spherical symmetry are the Schwarzschild solutions which include inner and external ones. We consider a static and uniform sphere with radius 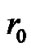 and constant density
and constant density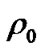 , inner pressure intensity
, inner pressure intensity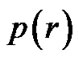 is related to coordinate but does not depends on time. By considering static energy momentum tensor of idea fluid, the Schwarzschild inner solution is [1,2].
is related to coordinate but does not depends on time. By considering static energy momentum tensor of idea fluid, the Schwarzschild inner solution is [1,2].
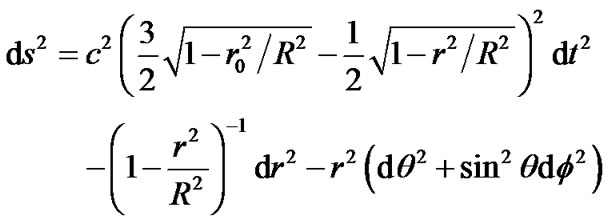 (1)
(1)
here . The metric is finite at the center point of sphere. However, it should be pointed out that in the process of solving the Einstein’s equation of gravity field, what we obtain is actually
. The metric is finite at the center point of sphere. However, it should be pointed out that in the process of solving the Einstein’s equation of gravity field, what we obtain is actually
 (2)
(2)
It can be proved based on (2) that the space curvature is infinite at point . In order to avoid the infinity, we let integral constant
. In order to avoid the infinity, we let integral constant 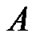 to be zero directly in the current theory. However, according to the theory of differential equation, integral constant should be determined by the known boundary conditions on spherical surface, in stead of the metric at the spherical center which is unknown. By considering the fact that the volume of sphere in curved space is different from that in flat space, we can prove
to be zero directly in the current theory. However, according to the theory of differential equation, integral constant should be determined by the known boundary conditions on spherical surface, in stead of the metric at the spherical center which is unknown. By considering the fact that the volume of sphere in curved space is different from that in flat space, we can prove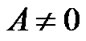 . Therefore, no matter what the mass and density of solid sphere are, the curvature infinity at the center of sphere is inevitable.
. Therefore, no matter what the mass and density of solid sphere are, the curvature infinity at the center of sphere is inevitable.
On the other hand, according to the current theory, the inner pressure intensity of sphere is [3].
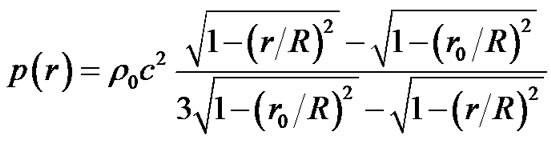 (3)
(3)
On the spherical surface  we have
we have . To make pressure intensity to be finite at the center of sphere, we have to introduce a constraint condition for spherical radius with
. To make pressure intensity to be finite at the center of sphere, we have to introduce a constraint condition for spherical radius with
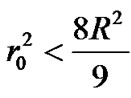 or
or  (4)
(4)
here 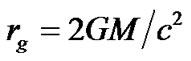 is the Schwarzschild radius. If
is the Schwarzschild radius. If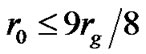 , pressure intensity will become infinite. In this case, stable solution is impossible and material would collapse towards the center of sphere so that singularity black holes appear. However, if integral constant
, pressure intensity will become infinite. In this case, stable solution is impossible and material would collapse towards the center of sphere so that singularity black holes appear. However, if integral constant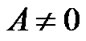 , pressure intensity (3) and constraint condition (4) will be changed. All calculations based on (3) and (4) about high density celestial bodies in the current astrophysics should be reconsidered.
, pressure intensity (3) and constraint condition (4) will be changed. All calculations based on (3) and (4) about high density celestial bodies in the current astrophysics should be reconsidered.
Let’s first strictly calculate the solutions of gravity field equations of hollow and solid spheres, and then discuss the problems of singularities below.
2. The Strict Inner Solution of Gravity Field of Hollow Sphere
Suppose that the inner radius of hollow sphere is  and the external radius is
and the external radius is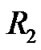 , the gravity mass is
, the gravity mass is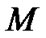 . The region
. The region 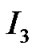 with
with  and the region
and the region  with
with 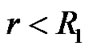 are vacuum. The region
are vacuum. The region  inside two spherical shells with
inside two spherical shells with  is composed of complete liquid with constant density
is composed of complete liquid with constant density  and pressure intensity
and pressure intensity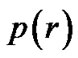 . Because material is distributed with spherical symmetry, the metric can be written as
. Because material is distributed with spherical symmetry, the metric can be written as
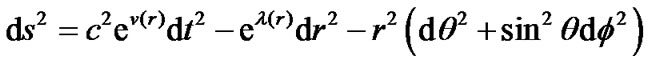 (5)
(5)
The solution of the Einstein’s equation of gravity in the region 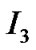 is the well-known Schwarzschild metric with
is the well-known Schwarzschild metric with

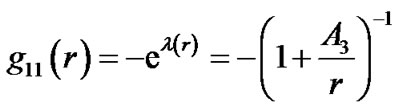 (6)
(6)
In order to determine integral constant , we compare (6) with the Newtonian theory under the asymptotic condition with
, we compare (6) with the Newtonian theory under the asymptotic condition with 
 ,
, 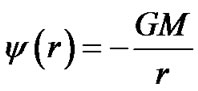 (7)
(7)
Here  is the static gravity mass of hollow sphere in the Newtonian theory. By comparing (6) with (7), we obtain
is the static gravity mass of hollow sphere in the Newtonian theory. By comparing (6) with (7), we obtain . So we have the same result for hollow sphere
. So we have the same result for hollow sphere
 ,
,  (8)
(8)
To calculate the metric in the region 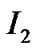 beneath two spherical shells, the mixing energy momentum tensor of complete fluid is used [1]
beneath two spherical shells, the mixing energy momentum tensor of complete fluid is used [1]
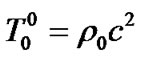 ,
,  ,
, (9)
(9)
The Einstein’s equation of gravity field is
 (10)
(10)
According to the standard procedure of calculation in general relativity, we obtain
 (11)
(11)
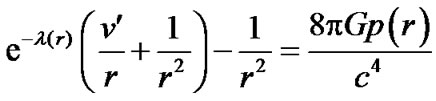 (12)
(12)
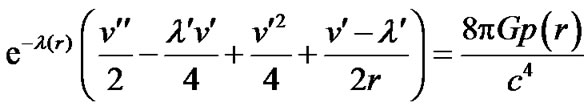 (13)
(13)
The integral of (11) is
 (14)
(14)
In which  and
and 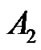 is an integral constant. We will prove
is an integral constant. We will prove  in the next section. (12) minus (13) then multiplied by
in the next section. (12) minus (13) then multiplied by 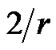 and considering (11), we obtain
and considering (11), we obtain
 (15)
(15)
The integral of (15) is
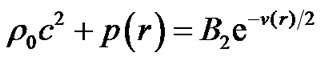 (16)
(16)
here  is an integral constant. By considering (11), (12) and (16), we obtain
is an integral constant. By considering (11), (12) and (16), we obtain
 (17)
(17)
On the other hand, by taking the differential of (14) with respect to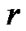 , we get
, we get
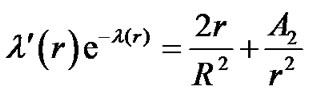 (18)
(18)
Substituting (14) and (18) in (17), we get
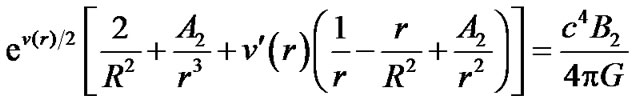 (19)
(19)
By considering the relation , (19) can be written as
, (19) can be written as
 (20)
(20)
here

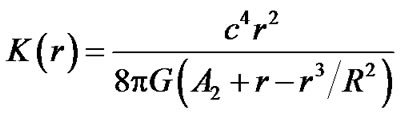 (21)
(21)
The integral of (20) is
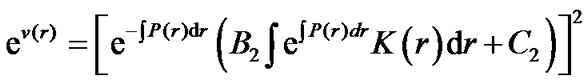 (22)
(22)
here  is an integral constant. If let
is an integral constant. If let  in (14) and (21), we reach the result of current theory [1]
in (14) and (21), we reach the result of current theory [1]
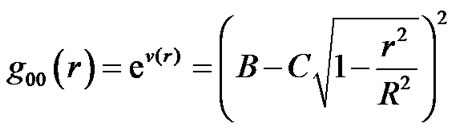
 (23)
(23)
In which constants ,
, . If
. If , we have
, we have
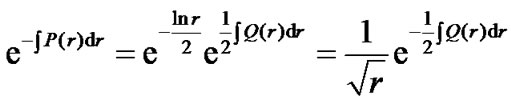 (24)
(24)
here
 (25)
(25)
let
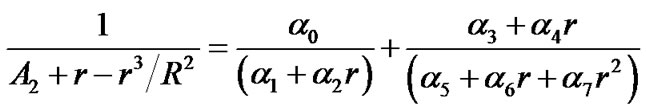 (26)
(26)
The forms of constants 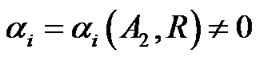 are complex, but it is unnecessary for us to write them out. We have
are complex, but it is unnecessary for us to write them out. We have
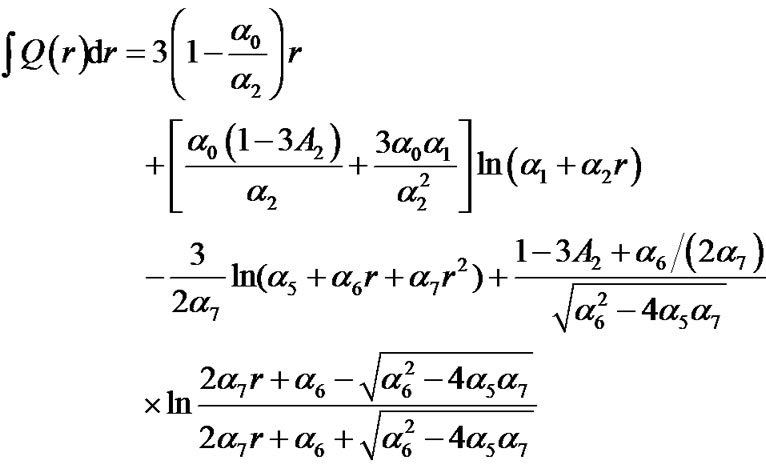
(27)
we write

(28)
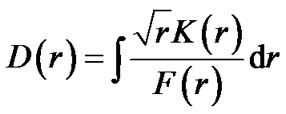 (29)
(29)
let  in (28), we get
in (28), we get
 (30)
(30)
Therefore, 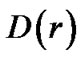 is finite at point
is finite at point . We can write (22) as
. We can write (22) as
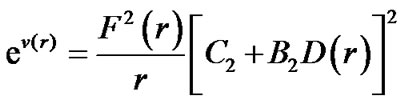 (31)
(31)
In the region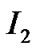 , the metric can be written as at last
, the metric can be written as at last
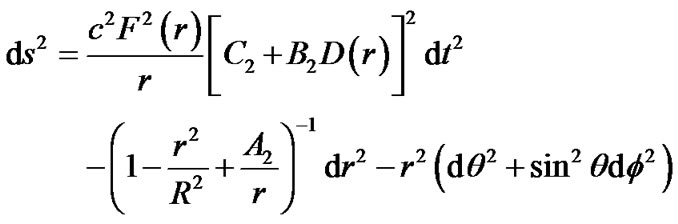
(32)
In the vacuum region 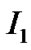 of hollow sphere cavity, the solution of the Einstein’s equation of gravity field is still the Schwarzschild solution
of hollow sphere cavity, the solution of the Einstein’s equation of gravity field is still the Schwarzschild solution
 ,
,  (33)
(33)
Let’s determine the integral constants ,
,  ,
,  and
and  below.
below.
3. The Calculations of Integral Constants for Hollow Sphere
By considering the continuity of metric tensors on the external spherical surface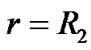 , according to (8), (14) and (32), we have
, according to (8), (14) and (32), we have
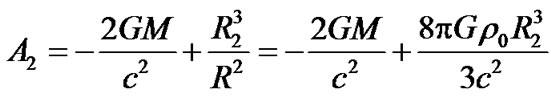 (34)
(34)
 (35)
(35)
Similarly, on the internal sphere surface with , according to (14), (33), (35) and (36), we have
, according to (14), (33), (35) and (36), we have
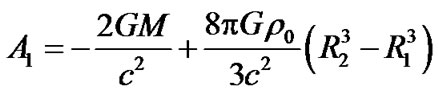 (36)
(36)
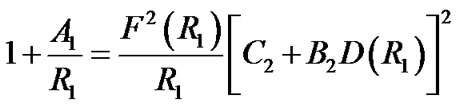 (37)
(37)
Let’s prove  in curved space now. If space is flat, the relation between mass
in curved space now. If space is flat, the relation between mass 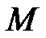 and volume
and volume 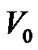 of hollow sphere is
of hollow sphere is  with
with
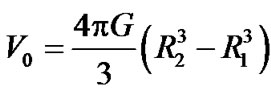 (38)
(38)
It should be emphasized that 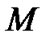 is the Newtonian gravity mass. We introduce it by considering the asymptotic relation (7) between the Einstein’s theory and the Newtonian theory of gravity. Substitute (38) in (37), we get
is the Newtonian gravity mass. We introduce it by considering the asymptotic relation (7) between the Einstein’s theory and the Newtonian theory of gravity. Substitute (38) in (37), we get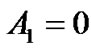 . This is just the current calculating result of general relativity.
. This is just the current calculating result of general relativity.
However, (38) can not hold in curved space. Because there is a length contraction along the direction of radiuswe should have 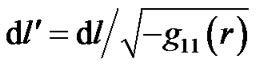 and
and , so
, so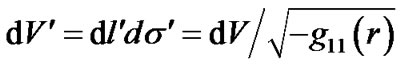 . In the curved space, the volume should be calculated by the following formula
. In the curved space, the volume should be calculated by the following formula
 (39)
(39)
The integral of (39) is difficult. If the third item in radical sign is neglected, we obtain [1].
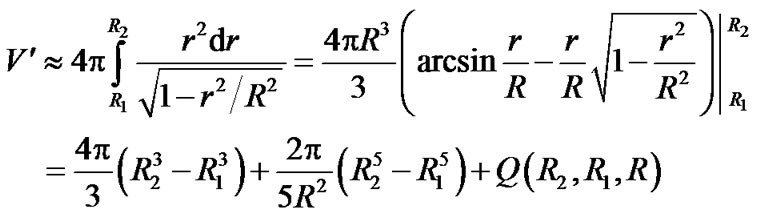
(40)
If we consider factor  in (39), the integral becomes more complex. So in curved space, we have:
in (39), the integral becomes more complex. So in curved space, we have:
 (41)
(41)
Substitute (41) in (37), we get
 (42)
(42)
Because ,
, 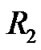 and
and  can be chosen arbitrarily, we have
can be chosen arbitrarily, we have  and
and  in general. Therefore, from (35) and (37), we obtain
in general. Therefore, from (35) and (37), we obtain
 (43)
(43)
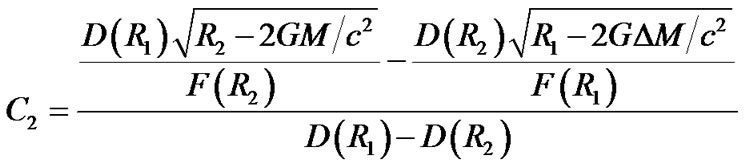
(44)
Similarly, because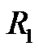 ,
, 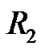 and
and 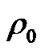 are arbitrary, we have
are arbitrary, we have 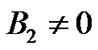 and
and  in general. In this way, all integral constants are determined. In the region
in general. In this way, all integral constants are determined. In the region  of spherical cavity, we can write (33) as
of spherical cavity, we can write (33) as
 ,
, 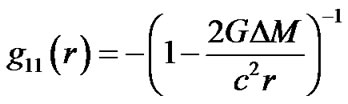 (45)
(45)
According to the Newtonian theory, the material distributed outside the spherical cavity with spherical symmetry does not affect the gravity field in the cavity. But according to (45), it will have some effect for the cavity.
4. The Singularity of the Inner Metric of Hollow Sphere
According to (45), the metric 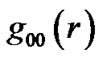 and curvature has singularity at the point
and curvature has singularity at the point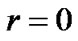 . This is inherent singularity which can not be eliminated by the coordinate transformation. The seriousness of problem is that for any hollow sphere composed of common material, no matter what are its mass and density, singularity always exists at its center. This does not agree with practical observation. It is impossible actually. On the other hand, we consider (14) and let
. This is inherent singularity which can not be eliminated by the coordinate transformation. The seriousness of problem is that for any hollow sphere composed of common material, no matter what are its mass and density, singularity always exists at its center. This does not agree with practical observation. It is impossible actually. On the other hand, we consider (14) and let
 or
or 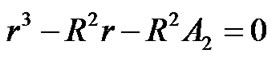 (46)
(46)
It seems that there is a singularity surface beneath two spherical shells. We now discuss this problem. The real number solution of (46) is
 (47)
(47)
However, if 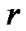 is really a real number, the following relation should be satisfied
is really a real number, the following relation should be satisfied
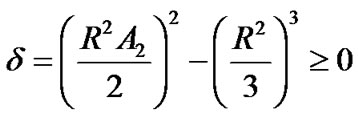 (48)
(48)
Let 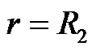 in (46) and considering (34), we have
in (46) and considering (34), we have
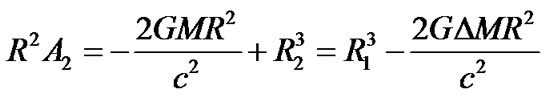 (49)
(49)
In the weak field, the item containing 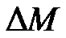 can be neglected. By considering (48) and (49), we get
can be neglected. By considering (48) and (49), we get
 (50)
(50)
We know that even for high density celestial body just as white dwarf, the difference is still very small when we do calculation based on both general relativity and the Newtonian theory. The material density of white dwarf is 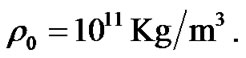 By using this value in (50), we get
By using this value in (50), we get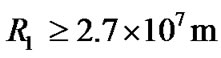 , similar to the size of white dwarf. For common galaxy, we have
, similar to the size of white dwarf. For common galaxy, we have  By using this value in (50), we have
By using this value in (50), we have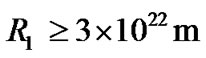 , which is just the size of galaxies. So (50) can be satisfied for common spheres and (47) becomes
, which is just the size of galaxies. So (50) can be satisfied for common spheres and (47) becomes
 (51)
(51)
By developing (51) into the Taylor series, if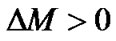 , we have
, we have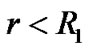 . That is to say, there is a singularity surface in the cavity. Because the metric of cavity is (33), in stead of (14), there is no singularity surface in the region
. That is to say, there is a singularity surface in the cavity. Because the metric of cavity is (33), in stead of (14), there is no singularity surface in the region 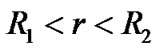 inside the hollow sphere. If
inside the hollow sphere. If , we have
, we have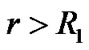 . In this case, there is a singularity surface in the region
. In this case, there is a singularity surface in the region .
.
According to (16), the pressure intensity in the hollow sphere is
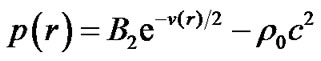

(52)
If there is a surface with radius 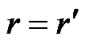 inside the hollow sphere on which we have
inside the hollow sphere on which we have
 (53)
(53)
The pressure intensity on the surface will become infinite. Therefore, if there exists black hole in hollow sphere, the black hole would be a spherical surface. Substitute (44) and (45) in (53), we get
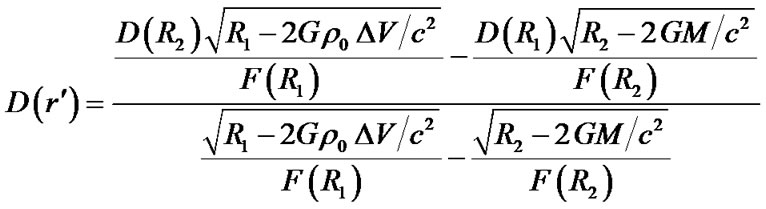
(54)
Because the radii  and
and  are arbitrary, from (54) that we may find a proper
are arbitrary, from (54) that we may find a proper 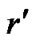 so that (68) can be satisfied. However, on this spherical surface composed of black holes, space-time has no singularity. That is to say, the surface of space-time singularity does not overlap with the surface on which material collapses. This is incomprehensible. It should be noted that up to now we have no any restriction on the mass and density of hollow sphere. This result indicates that common hollow spheres may be unstable. They may collapse into the black hole of spherical surface!
so that (68) can be satisfied. However, on this spherical surface composed of black holes, space-time has no singularity. That is to say, the surface of space-time singularity does not overlap with the surface on which material collapses. This is incomprehensible. It should be noted that up to now we have no any restriction on the mass and density of hollow sphere. This result indicates that common hollow spheres may be unstable. They may collapse into the black hole of spherical surface!
Similarly, because the internal and external radii are arbitrary, let 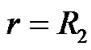 or
or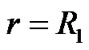 , we have
, we have 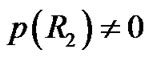 and
and 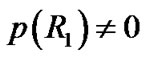 in general. Because the hollow sphere is placed in vacuum without material outside and inside its two surfaces, this result is also incomprehensible. The singularities of hollow sphere are shown in Figure 1. It is obvious that the results can not be true.
in general. Because the hollow sphere is placed in vacuum without material outside and inside its two surfaces, this result is also incomprehensible. The singularities of hollow sphere are shown in Figure 1. It is obvious that the results can not be true.
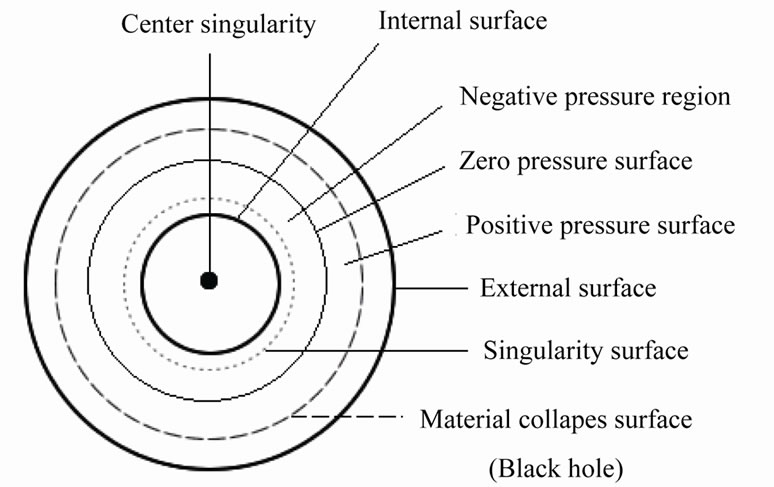
Figure 1. The singularity of hollow sphere.
5. The Singularities of Solid Sphere’s Metric and Black Holes
According to the present calculation of general relativity, the internal metric of a common solid sphere has no singularity when the radius of sphere is greater than the Schwarzschild radius. According to the strict calculation in this paper, the situation is completely different. The solid sphere is a special situation of hollow sphere when its internal radius becomes zero. The internal metric of solid sphere is still described by (30), but the conditions of boundary are different. On the spherical surface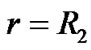 , we have
, we have
 (55)
(55)
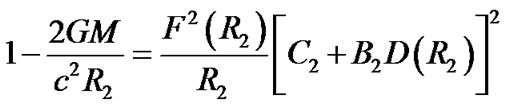 (56)
(56)
In order to determine 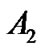 in (55), we have to know the relation between
in (55), we have to know the relation between  and
and . In curved space, we have
. In curved space, we have
 (57)
(57)
By substituting (57) in (55), we can decide  in principle. We have
in principle. We have 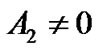 in general. If suppose
in general. If suppose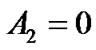 , we have
, we have
 (58)
(58)
Because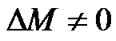 , the boundary condition (55) can not be satisfied. We estimate the magnitude of volume’s change in curved space based on (58). Let
, the boundary condition (55) can not be satisfied. We estimate the magnitude of volume’s change in curved space based on (58). Let  and omitting high order items, we have
and omitting high order items, we have
 (59)
(59)
For neutron stars, we have 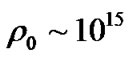 and
and , so
, so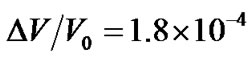 . If considering the universe as a uniform sphere, we have
. If considering the universe as a uniform sphere, we have 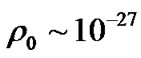 and
and , so
, so . For so-called black hole, we have
. For so-called black hole, we have  according to (4) and
according to (4) and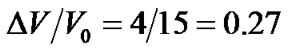 . For common spheres just as the sum and the earth,
. For common spheres just as the sum and the earth, 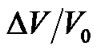 is a very small but non-zero quantity.
is a very small but non-zero quantity.
After  is determined, by substituting it into (28) and (29), we can determine
is determined, by substituting it into (28) and (29), we can determine 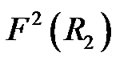 and
and . However, we can not yet determinate
. However, we can not yet determinate 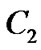 and
and 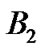 only based on (56). Another condition is needed. By considering the fact that the pressure intensity on the surface of sphere should be zero with
only based on (56). Another condition is needed. By considering the fact that the pressure intensity on the surface of sphere should be zero with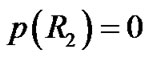 , from (16) and (31) we have
, from (16) and (31) we have
 (60)
(60)
From (56) and (60), we obtain
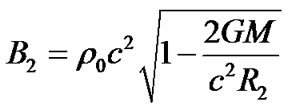
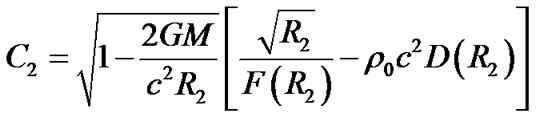 (62)
(62)
Now, all integral constants are determined. The internal metric of solid sphere is
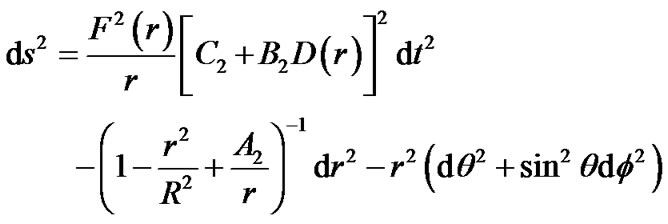 (63)
(63)
Because 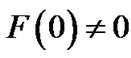 and
and 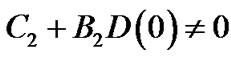 in general, we have
in general, we have  and
and  at point
at point so the infinite of space-time curvature also appears at the center of sphere.
so the infinite of space-time curvature also appears at the center of sphere.
The pressure intensity of solid sphere is also represented by (52), but the integral constants should be represented by (61). In general, we have  and
and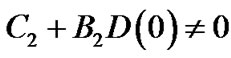 , so we have
, so we have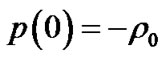 . That is to say, no mater what are the mass and density of sphere, the pressure intensity at the center of sphere can not be infinite. So-called the singularity black holes in which material collapses towards its center are impossible. Meanwhile, the pressure intensity may become negative value at the center of sphere and its nearby region too. On the other hand, if there is spherical surface with radius
. That is to say, no mater what are the mass and density of sphere, the pressure intensity at the center of sphere can not be infinite. So-called the singularity black holes in which material collapses towards its center are impossible. Meanwhile, the pressure intensity may become negative value at the center of sphere and its nearby region too. On the other hand, if there is spherical surface with radius 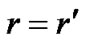 so that we have
so that we have
 (64)
(64)
the pressure intensity may become infinite on the surface. Substitute (61) in (63), we obtain
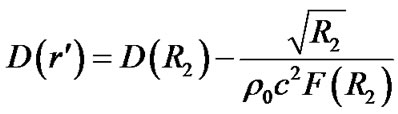 (65)
(65)
Therefore, if black hole exists in solid sphere, it can
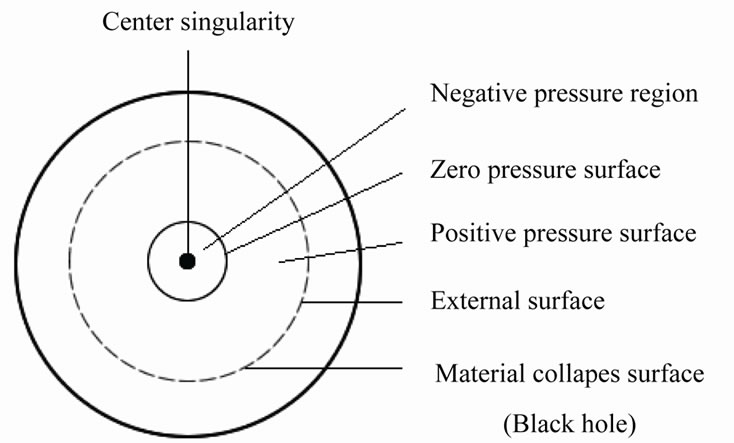
Figure 2. The singularity of solid sphere.
only take the form of a spherical surface. Such solid sphere is not stable for material will collapse to its spherical surface. But according to our common experiences there is no singularity of space-time curvature on the spherical surface. Such result is also uncanny.
The singularity of solid sphere is shown in Figure 2. Notice that we did not impose any restriction for mass and density, and there are so many strange characteristics for common solid spheres. The results are completely different from the current understanding in general relativity. The theory of singularity black hole in the current astrophysics and cosmology has to be reconsidered.
6. Discussions on the Theorem of Singularity and the Rationality of Current Singularity Black Hole Theory
S. W. Hawking etc. proved the theorem of singularity by means of the method of differential geometry [4]. The theorem was based on three prerequisite conditions. 1. General relativity was tenable. 2. The law of causality was tenable. 3. There were some points in space-time at which material densities were non-zero. The theorem claimed that if theses three conditions were satisfied, singularity inevitably existed in space-time. Hawking etc. considered singularities as the beginning and ending of time. The Big Bang theory was considered as the beginning of time and the black holes were regarded as the ending of time.
We note that the theorem had no restriction on material’s mass and density and did not demand that singularities were embodied in material. That is to say, according to the theorem, singularities may bare in vacuum. In order to avoid this embarrassing situation, Penrose proposed the so-called principle of the universe supervisor. The principle declares that there exists the universe supervisor who prohibit the appearance of bare singularities in vacuum. In other word, due to the existence of the universe supervisors, all singularities will be wrapped in the centers of black holes with great masses and high densities. According to the solutions of the Einstein’s equation of gravity, there exist Schwarzschild black holes with spherical symmetry and the Kerr black holes with axial symmetry and so on. The singularities were hidden in the centers of material. In this way, they can not be perceived directly, and physicists seem tolerate their existence.
The results revealed in the paper are consistent with the Hawking theorem of singularity actually. We can consider them as the practical examples of the theorem. By considering the fact that the volume of hollow and solid spheres in curved space are different from that in flat space, the strict calculation reveals that singularities can not be avoided at the centers of common hollow and solid spheres with small masses and low densities. On the other hand, because the pressure intensity can not be infinite at the center of sphere, material can not collapse towards the spherical center. Also the result shows that the pressure intensity may become negative values at the center and its nearby region.
Meanwhile, there may be curved surfaces inside the common hollow and solid spheres on which pressure intensities can become infinite so that material will collapse to them. But the space-time curvatures are still finite on the surfaces. The surfaces of space-time singularity do not always overlap with the surfaces with infinite pressure intensities. All these characters can not agree with our practical experiences of common hollow and solid spheres. They are incomprehensible in physics.
According to the current understanding, the black holes exist at the center of Quasars. However, according to the observations of Rudolf E. Schild and Darryl J. Leiter, the center of Quasar 0957 + 561 is a close object, called MECO (Massive Eternally Collapsing Object) [5]. It is not a singularity black hole, and is surrounded by a strong magnetic field. The observation of Rudolf E. Schild was consistent with the calculation and analyses in this paper. That is to say, if there are black holes in the universal space, they can only be the Newtonian black holes, not the Einstein’s singularity black holes!
More essentially, the true world excludes infinites. A correct theory of physics can not tolerate the existence of infinites, especially singularities in daily life’s hollow and solid spheres composed of common material. It is well known that the history of physics is one to overcome infinites. Modern physics grows up in the process to surmount infinites. As revealed in this paper, singularity in general relativity is actually caused by the description method of curved space-time. Physicists and cosmologists should take cautious and incredulous attitude toward the problems of singularity black holes. It is not a scientific attitude to consider singularity black holes as objective existence without any question to them. We should think in deep, whether or not our theory has something wrong. When we enjoy the beauty and symmetry of the Einstein’s theory of gravity, remember that we should not neglect its limitations and possible mistake.
7. References
[1] J. R. Oppenheimer and H. Snyder, “On Continued Gravitational Contraction,” Physical Review, Vol. 56, No. 5, 1939, pp. 455-459. doi:10.1103/PhysRev.56.455
[2] Y. L. Zhang, “Introduce to Relativity,” The Publishing Company of Yunnan People, Kunming, 1989, p. 388.
[3] L. B. Feng, X. C. Liu and M. C. Li, “Genarel Relativity,” Jilin Science Publishing Company, Jilin, 1995, p. 109.
[4] S. W. Hawking and G. F. R. Eills, “The Large Scale Structure of Space Time,” Cambridge University Press, New York, 1972.
[5] R. E. Schild, D. J. Leiter and S. L. Robertson, “Black Hole or Meco: Decided by a Thin Luminous Ring Structure Deep within Quasar Q0957 + 561,” Journal of Cosmology, Vol. 6, 2010, pp. 1400-1437.

