International Journal of Astronomy and Astrophysics
Vol.1 No.1(2011), Article ID:4372,5 pages DOI:10.4236/ijaa.2011.11001
Effect of Interplanetary Matteron the Spin Evolutions of Venus and Mercury
1College of Physics and Electronics, Shandong Normal University, Jinan, China
2Mullard Space Science Laboratory, University College London, Dorking, UK
3Department of Physics and Electronic Engineering, Zaozhuang University, Zaozhuang, China
E-mail: nieqx@126.com
Received February 20, 2011; revised March 2, 2011; accepted March 7, 2011
Keywords: Schrödinger Equation; Planets Rotation; Planets Revolution
Abstract
Differs from other planets in the Solar System, the Venus has a retrograde and long-period rotation. To explain the special spin of the Venus, mechanisms such as core mantle friction inside planet [1], atmospheric tide [2-7], or twain effects together [8-11], and impact with a giant object [12,13] have been suggested. These mechanisms, however, need specific initial conditions with a remote probability [3,5]. The slow spin of Mercury cannot be explained very well. One viewpoint is that the unusual spins of Venus and Mercury might be naturally evolved from similar initial states by interaction with interplanetary matter during longtime evolution. Based on the theory of planet formation and the orderliness of planetary distance, we discuss the possibility that the radial density distribution of interplanetary matter is undulated, and the wave function satisfies the formal Schrödinger equation. We calculate the evolution of planet spins under the effect of interplanetary matter during planets revolution and rotation. The results show that planets can naturally evolve to the current state (particularly the negative spin of the Venus) given the similar initial quick and positive spins.
1. Introduction
The regular distribution of planets in the Solar System implies that the density distribution of the original nebular disk undulated, which played important role on planets growth and spin. During the formation of the Solar System, nebular particles behave as random thermal motion and concurrent revolution around the Sun. It is impossible to trace each particle in microcosmic scope. However, nebular particles follow a probability orbit, the so-called Keplerian orbit. We attempt to describe the probability orbits of nebular particles in the Solar System by using the wave function 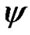 as we do to describe the probability orbits of electrons in the atom system, which satisfies the formal Schrödinger equation,
as we do to describe the probability orbits of electrons in the atom system, which satisfies the formal Schrödinger equation,
 (1)
(1)
where G is gravitational constant,  and M are masses of the nebular particle and the Sun, respectively, r is the distance between the particle and the Sun, K is the large-scale constant. If total energy
and M are masses of the nebular particle and the Sun, respectively, r is the distance between the particle and the Sun, K is the large-scale constant. If total energy , the normalized radial function is
, the normalized radial function is
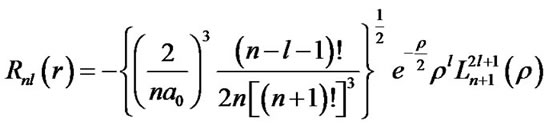 (2)
(2)
where
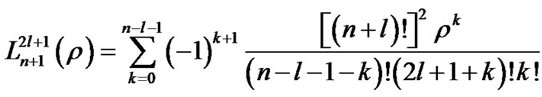 ,
,
 ,
, ,
, , and
, and .
.
 Based on the equiprobability principle, the radial probability density of the nebular particles is expressed as
Based on the equiprobability principle, the radial probability density of the nebular particles is expressed as
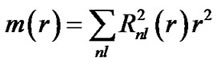 (3)
(3)
It has been found that the protosolar cloud is composed of ~0.71 hydrogen, ~0.27 helium, and ~0.02 heavy elements [14]. The interplanetary space is filled with atomic hydrogen [15], since H2 molecules are very vulnerable to photons with energies below the Lyman limit [16]. The distributions of H and He play crucial role on the formation and evolution of planets. From , we take
, we take  AU for H, and
AU for H, and 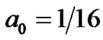 AU for He. The calculated
AU for He. The calculated 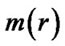 for H is shown in Figure 1(a). Significant facts were found by Nie[17,18] that the giant planets and the center of the Kuiper Belt are all at the wave crests, and their masses order is almost consistent with that of the amplitude of
for H is shown in Figure 1(a). Significant facts were found by Nie[17,18] that the giant planets and the center of the Kuiper Belt are all at the wave crests, and their masses order is almost consistent with that of the amplitude of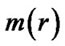 , the terrestrial planets including the Earth are all in the first wave, and their masses order is consistent with that of the intensity of
, the terrestrial planets including the Earth are all in the first wave, and their masses order is consistent with that of the intensity of . The calculated
. The calculated  for He is shown in the bottom wave line of Figure 1(b). It is found that each terrestrial planet is located in a separate wave of He from second to the fifth, and the Asteroid Belt is located in the sixth wave. The intensity of H is too small to form planet in the first wave of He.
for He is shown in the bottom wave line of Figure 1(b). It is found that each terrestrial planet is located in a separate wave of He from second to the fifth, and the Asteroid Belt is located in the sixth wave. The intensity of H is too small to form planet in the first wave of He.
Here 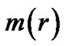 is the non-normalized probability density of interplanetary matter. To calculate planets rotation, the mass density
is the non-normalized probability density of interplanetary matter. To calculate planets rotation, the mass density should be given by
should be given by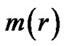 and the near-Earth mass density
and the near-Earth mass density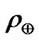 . Based on HST [19-22] observations of the nebular disks around the young stars, it is known that most of the interplanetary matter is distributed in the nebular disk. The thickness of the nebular disk is expressed as
. Based on HST [19-22] observations of the nebular disks around the young stars, it is known that most of the interplanetary matter is distributed in the nebular disk. The thickness of the nebular disk is expressed as
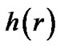 . For instance,
. For instance, 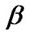 = 1.10-1.32 for HK Tau/c [20], 9/8 for Orion 114-426 [21], 1.29 for IRAS 04302+2247 [22], and 1.25 for HH 30 IRS [23]. Here we take
= 1.10-1.32 for HK Tau/c [20], 9/8 for Orion 114-426 [21], 1.29 for IRAS 04302+2247 [22], and 1.25 for HH 30 IRS [23]. Here we take  when
when  AU in the solar system. Taking
AU in the solar system. Taking 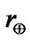 to be the distance of Earth from the Sun,
to be the distance of Earth from the Sun, 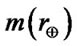 probability density in the near Earth space, and
probability density in the near Earth space, and 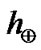 the scale height of the nebular disk at
the scale height of the nebular disk at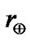 , due to
, due to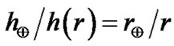 and
and 
 ,
, can be expressed as
can be expressed as
 (4)
(4)
2. Spin Evolution
To calculate the evolution of planets spin, two models for planets revolution and rotation should be established. Assuming the planet spin axis is perpendicular to the orbital plane and the spin is anticlockwise similar to its revolution. We take the radius of the planet Hill sphere as R. Drawing a thin ring with the width  on the surface of the Hill sphere which is perpendicular to the line connecting the Sun with the planet, and letting r and
on the surface of the Hill sphere which is perpendicular to the line connecting the Sun with the planet, and letting r and 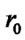 are the heliocentric distances of the ring center and the planet center, the spin angular momentum obtained during the period of revolution by the ring in collision with
are the heliocentric distances of the ring center and the planet center, the spin angular momentum obtained during the period of revolution by the ring in collision with
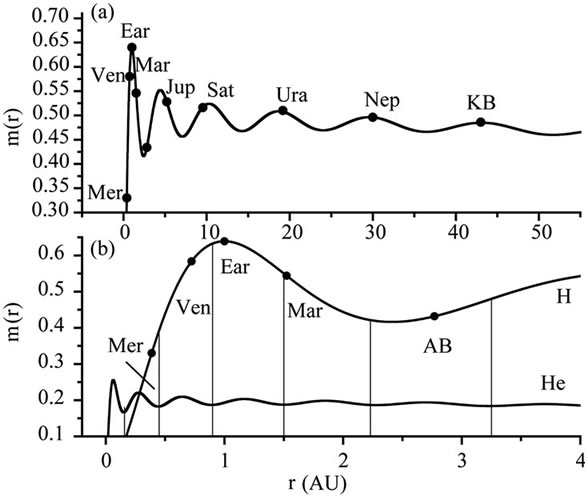
Figure 1. Radial probability density distribution of interplanetary matter. Upper panel a) is the distribution of H with 3/4 of the nebular mass. Giant planets and the center of Kuiper Belt are all at the wave crests. Terrestrial planets are all at the first wave. Bottom panel b) is the distribution of He with 1/4 of the nebular mass and the first wave of H. Each terrestrial planet lies at a separate wave of He. It is interesting that the Kuiper Belt and Asteroid Belt lie in the sixth wave of H and He, and the widths of belts are consistent with wavelengths, respectively.
interplanetary matter is
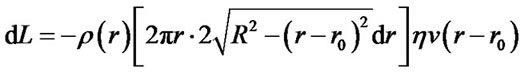 (5)
(5)
where  is the revolution velocity of a planet,
is the revolution velocity of a planet, 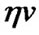 is the relative velocity of planets to interplanetary gas. Theory of the origin of the solar system suggests that solids and gas do not have the same angular velocities in solar nebula, and angular velocity of the gas is smaller than that of a large body [24], so
is the relative velocity of planets to interplanetary gas. Theory of the origin of the solar system suggests that solids and gas do not have the same angular velocities in solar nebula, and angular velocity of the gas is smaller than that of a large body [24], so . Assuming
. Assuming 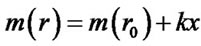 in the scale of the planet, where
in the scale of the planet, where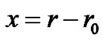 ,and taking the angular velocity of revolution to be
,and taking the angular velocity of revolution to be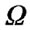 , the integral of Equation (5) is
, the integral of Equation (5) is
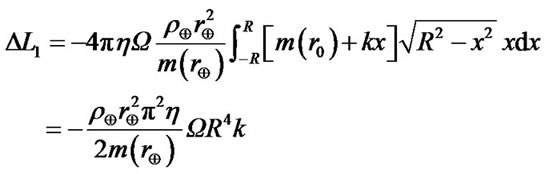 (6)
(6)
This is the angular momentum obtained by the planet during the period of revolution. If the curvilinear slope or derivative of ,
,  , the spin angular momentum is decreasing, this is the case of the Venus and Mercury.
, the spin angular momentum is decreasing, this is the case of the Venus and Mercury.
Assuming the planet as a sphere with uniform density, the moment of inertia is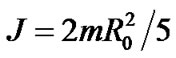 , where m is the planet mass,
, where m is the planet mass,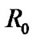 planetary object radius. Using
planetary object radius. Using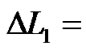 ,
, 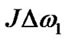 the increment of angular velocity is
the increment of angular velocity is
 (7)
(7)
The resistance of interplanetary matter during the planet rotation could also slow down its spin velocity. During a period of revolution, the mass of interplanetary matter interacting with the planet Hill sphere is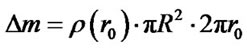 . Based on the conservation of angular momentum
. Based on the conservation of angular momentum ignore the second order, then
ignore the second order, then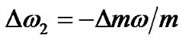 ,where
,where  is spin angular velocity. Using
is spin angular velocity. Using
 ,the increment of angular velocity is
,the increment of angular velocity is
 (8)
(8)
During a period of revolution, the increment of the spin angular velocity is ,and the planet spin angular acceleration can be expressed as
,and the planet spin angular acceleration can be expressed as
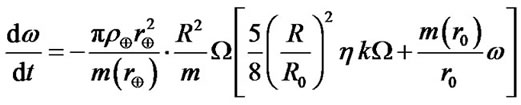 (9)
(9)
Assuming the revolution angular velocity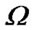 ,the planet mass m, and the Hill sphere radius R are constants, so the mass density
,the planet mass m, and the Hill sphere radius R are constants, so the mass density 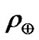 is the only variable in Equation (9). Referring to the method for studying the nebular disks around sun-like stars [25], the mass of the disk decreases as
is the only variable in Equation (9). Referring to the method for studying the nebular disks around sun-like stars [25], the mass of the disk decreases as . Due to the effect of solar wind, the evolution of
. Due to the effect of solar wind, the evolution of 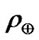 can be worked out by solving equation
can be worked out by solving equation  to give
to give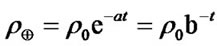 , where
, where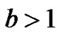 . The planet spin angular velocity is derived by integral of equation (9) as
. The planet spin angular velocity is derived by integral of equation (9) as
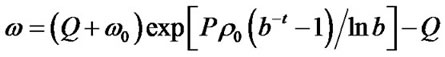 (10)
(10)
where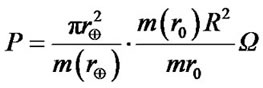 ,and
,and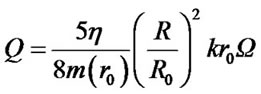 .
.
Taking current time , then
, then  and
and 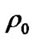 are the current spin angular velocity and mass density in near-Earth space, respectively. Here
are the current spin angular velocity and mass density in near-Earth space, respectively. Here 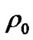 and b should be clarified. The mass density of interplanetary dust have been estimated to be
and b should be clarified. The mass density of interplanetary dust have been estimated to be  kg/m3 [26], the ratio of dust to nebula is about 2%, then the density of interplanetary matter is about
kg/m3 [26], the ratio of dust to nebula is about 2%, then the density of interplanetary matter is about  kg/m3 . The hydrogen number density is ~104 cm–3 (the mass density is ~
kg/m3 . The hydrogen number density is ~104 cm–3 (the mass density is ~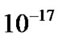 kg/m3) [27]. Here we take
kg/m3) [27]. Here we take  =
= kg/m3 =
kg/m3 = kg/AU3. Taking
kg/AU3. Taking  as the mass density at 4.5 Gyr (the Earth age) ago, then
as the mass density at 4.5 Gyr (the Earth age) ago, then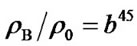 . We estimate b by Equation (10). It is found that the effects of mass density change (
. We estimate b by Equation (10). It is found that the effects of mass density change (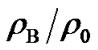 ) on the planetary rotation periods are different for different planet, it is obvious for Venus and Mercury, but unobvious for other planets. For
) on the planetary rotation periods are different for different planet, it is obvious for Venus and Mercury, but unobvious for other planets. For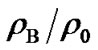 ~ 109, according to b = 1.585, the periods of the terrestrial planets are all close to one day, which are typical and expected values. Taking Hill sphere radius
~ 109, according to b = 1.585, the periods of the terrestrial planets are all close to one day, which are typical and expected values. Taking Hill sphere radius ,
, 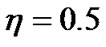 and
and 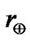 = 1 AU,
= 1 AU, 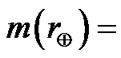 0.64, and
0.64, and 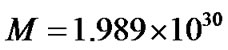 kg, the other parameters are derived and shown in Table 1.
kg, the other parameters are derived and shown in Table 1.
Furthermore, the evolution of spin periods of the Venus and Mercury are shown in Figure 2. It is found that the spin of the Venus changes naturally from positive to retrograde around 3.5 Gyr ago, the period is from the initial about 3 day to the current – 243 day; the spin of the Mercury changes from quick to slow, the period is from the initial about 1 day to the current 58.6 day. Another fact should be noticed that the spins of the two planets remain almost steady from about 3 Gyr ago until the foreseeable future.
Appling Equation (10) to other planets, their spins change slightly. In detail, the period of the Earth decreases 0.01 days, the Mars increases 1.3 days, the Jupiter decreases 0.02 days, the changes of Saturn and Neptune are much smaller. However, Equation (10) cannot be applied to the Uranus due to the particularity of its spin axis.

Figure 2. Evolution of the rotation periods of the Venus and Mercury in 4.5 billion years. From the initial spin period of 3.5 day to the current -243 day, the spin of the Venus experienced a reverse around 3.5 billion years ago and remained almost stable since then. From the initial spin period of 1 day to the current 58.7 day, the spin of the Mercury experienced a rapid slowing down around 3 billion years ago and then remained stable to present.
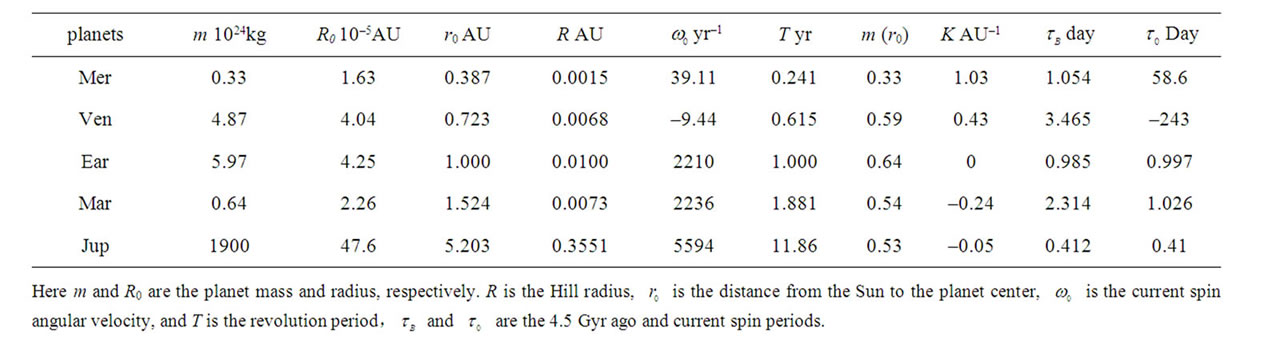
Table 1. The data for computing.
3. Conclusions
In summary, the probability orbits of nebular particles in the Solar System can be described by the wave function in large scale, which satisfies the formal Schrödinger equation. The radial density distribution of interplanetary matter is undulated as a wave line, and the curvilinear slopes of the wave line at the positions of the Venus and Mercury slow down their spins. The results show that the planets spins can evolve from the initial positive spins to the current state if the original interplanetary matter density is 109 times to the current one and has an exponential decrease with time. Especially, the retrograde of the Venus is a natural result of the asymmetric effect of interplanetary matter.
4. Acknowledgements
We would like to thank Prof. Chuanfu Cheng, Prof. Qingtian Meng, and Graduate student Chu Zhe for helpful discussions.
5. References
[1] A. C. M. Correia, “The Core Mantle Friction Effect on the Secular Spin Evolution of Terrestrial Planets,” Earth and Planetary Science Letters, Vol. 252, No. 3-4, 2006, pp. 398-412. doi:10.1016/j.epsl.2006.10.007
[2] W. Kundt, “Spin and atmospheric Tides of Venus,” Astronomy & Astrophysics, Vol. 60, No. 1, 1977, pp. 85-91.
[3] A. R. Dobrovolskis, “Atmospheric Tides and the Rotation of Venus. II-Spin Evolution,” Icarus, Vol. 41, 1980, pp. 18-35. doi:10.1016/0019-1035(80)90157-8
[4] J. McCue, J. R. Dormand and A. M. Gadian, “Estimates of Venusian Atmospheric Torque,” Engineering Management & Planning, Vol. 57, 1992, pp. 1-11.
[5] J. McCue and J. R. Dormand, “Evolution of the Spin of Venus,” Engineering Management & Planning, Vol. 63, 1993, pp. 209-225.
J. Laskar and P. Robutel, “The Chaotic Obliquity of the Planets,” Nature, Vol. 361, No. 6413, 1993, pp. 608-612. doi:10.1038/361608a0
[6] A. C. M. Correia, et al., “Long-Term Evolution of the Spin of VenusI. Theory,” Icarus, Vol. 163, 2003, pp. 1-23. doi:10.1016/S0019-1035(03)00042-3
[7] A. C. M. Correia and J. Laskar, “The Four Final Rotation States of Venus,” Nature, Vol. 411, No. 6839, 2001, pp. 767-770. doi:10.1038/35081000
[8] P. Goldreich and S. J. Peale, “The Obliquity of Venus,” The Astronomical Journal, Vol. 75, 1970, pp. 273-285. doi:10.1086/110975
[9] B. Lago and A. Cazenave, “Possible Dynamical Evolution of the Rotation of Venus since Formation,” M&P, Vol. 21, 1979, pp. 127-154.
[10] M. Shen and C. Z. Zhang, “Dynamical Evolution of the Rotation of Venus,” Engineering Management & Planning, Vol. 43, 1988, pp. 275-287.
[11] S. F. Singer, “How Did Venus Lose Its Angular Momentum,” Science, Vol. 170, No. 69, 1970, pp. 1196-1198. doi:10.1126/science.170.3963.1196
[12] S. Tremaine and L. Dones, “On the Statistical Distribution of Massive Impactors,” Icarus, Vol. 106, 1993, pp. 335-341. doi:10.1006/icar.1993.1175
[13] K. Lodders, “Solar System Abundances and Condensation Temperatures of the Elements,” The Astrophysical Journal, Vol. 591, No. 2, 2003, pp. 1220-1247. doi:10.1086/375492
[14] P. W. Blum and H. J. Fahr, “Interaction between Interstellar Hydrogen and the Solar Wind,” Astronomy & Astrophysics, Vol. 4, 1970, pp. 280-290.
[15] V. Bromm, A. Ferrara, P. S. Coppi and R. B. Larson, “The Fragmentation of Pre-Enriched Primordial Objects,” Monthly Notices of the Royal Astronomical Society, Vol. 328, No. 3, 2001, pp. 969-976. doi:10.1046/j.1365-8711.2001.04915.x
[16] Q. X. Nie, “Simulated Quantum Theory for Seeking the Mystery of Regularity of Planetary Distances,” Acta astronomy Sin., Vol. 34, 1993, pp. 333-340.
[17] Q. X. Nie, “The Characteristics of Orbital Distribution of Kuiper Belt objects,” Chin. J. Astron. Astrophys, Vol. 27, 2003, pp. 94-98.
[18] D. L. Padgett, et al., “Hubble Space Telescope/Nicmos Imaging of Disks and Envelopes around Very Young Stars,” The Astronomical Journal, Vol. 117, No.3, 1999, pp. 1490-1504. doi:10.1086/300781
[19] K. R. Stapelfeldt, et al., “An Edge-On Circumstellar Disk in the Young Binary System HK Tauri,” American Politics Journal, Vol. 502, 1998, pp. L65-L69.
[20] M. J. McCaughrean, et al., “High-Resolution Near-Infrared Imaging of the Orion 114-426 Silhouette Disk,” American Politics Journal, Vol. 492, 1998, L157-L161.
[21] S. Wolf, D. L. Padgett and K. R. Stapelfeldt, “The Circumstellar Disk of the Butterfly Star in Taurus,” American Politics Journal, Vol. 588, 2003, pp. 373-386.
[22] K. W. Wood, J. Michael, J. E. Bjorkman and B. Whitney, “The Spectral Energy Distribution of HH 30 IRS: Constraining the Circumstellar Dust Size Distribution,” American Politics Journal, Vol. 564, 2002, pp. 887-895.
[23] A. G. W. Cameron, “Origin of the Solar System,” Annual Review of Astronomy and Astrophysics, Vol. 26, 1988, pp. 441-472. doi:10.1146/annurev.aa.26.090188.002301
[24] M. C. Wyatt, R. Smith, J. S. Greaves, C. A. Beichman, G. Bryden and C.M. Lisse, “Transience of Hot Dust around Sun-Like Stars,” American Politics Journal, Vol. 658, 2007, pp. 569-583.
[25] P. R. Weissman, L. A. McFadden and T. V. Johnson, “Encyclopedia of the Solar System,” Academic Press, San Diego, 2006.
[26] E. Dwek, R. G. Arendt and F. Krennrich, “The Near-Infrared Background: Interplanetary Dust or Primordial Stars,” American Politics Journal, Vol. 635, 2005, pp. 784-794.

