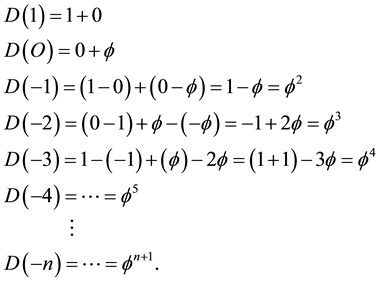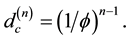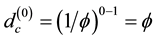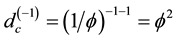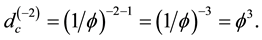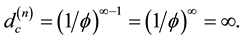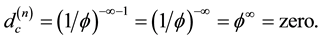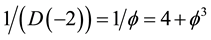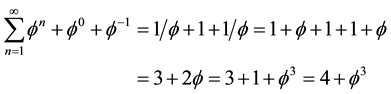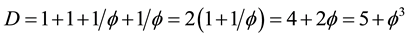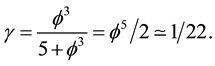World Journal of Nano Science and Engineering
Vol.05 No.03(2015), Article ID:58120,10 pages
10.4236/wjnse.2015.53008
Hubble Scale Dark Energy Meets Nano Scale Casimir Energy and the Rational of Their T-Duality and Mirror Symmetry Equivalence*
M. S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 June 2015; accepted 17 July 2015; published 20 July 2015
ABSTRACT
We establish that ordinary energy, Casimir energy and dark energy are not only interlinked but are basically the same thing separated merely by scale and topology. Casimir energy is essentially a nano scale spacetime phenomenon produced by the boundary condition of the two Casimir plates constituting the Casimir experimental set up for measuring the Casimir force. By contrast dark energy is the result of the cosmic boundary condition, i.e. the boundary of the universe. This one sided Möbius-like boundary located at vast cosmic distance and was comparable only to the Hubble radius scales of the universe. All the Casimir energy spreads out until the majority of it reaches the vicinity of the edge of the cosmos. According to a famous theorem due to the Ukrainian-Israeli scientist I. Dvoretzky, almost 96% of the total energy will be concentrated at the boundary of the universe, too far away to be measured directly. The rest of the accumulated Casimir energy density is consequently the nearly 4% to 4.5%, the existence of which is confirmed by various sophisticated cosmic measurements and observations. When all is said and done, the work is essentially yet another confirmation of Witten’s T-duality and mirror symmetry bringing nano scale and Hubble scale together in an unexpected magical yet mathematically rigorous way.
Keywords:
Mirror Symmetry, Casimir Energy, Dark Energy, Zero Point Vacuum Energy, T-Duality, Nano Scale-Hubble Scale, Möbius Holographic Boundary, Dvoretzky’s Theorem, Banach-Tarski Theorem

1. Introduction
The present paper is concerned with a wide range of problems connecting high energy quantum physics with relativity, quantum gravity and cosmology [1] - [96] .
One of the many memorable words of wisdom that Prof. Sir Herman Bondi was known for is to the effect that once a great truth about nature is uncovered, it becomes so obvious and self evident that we are bound to wonder how we did not notice it for such a long time and how it could have eluded us all despite its compelling simple logic [1] . Sir Herman used to cite Einstein’ relativity as his favourite parade example [1] - [10] .
Referring to the present work the author would like to think that the thesis that we are about to reveal belongs in the same category which Prof. Bondi would have liked [1] - [10] . We are pointing here at our discovery that we perceived a few months ago as tantalizing because it implies the realization that the Casimir energy involved in the famous Casimir effect as well as dark and ordinary energy density of the cosmos are nothing but different forms of the same physical reality by virtue of some mathematical theorem which goes by the name of mirror symmetry and T-duality [93] - [95] . With that we do not only mean that they are different manifestations of the zero point energy of vacuum fluctuation only [11] - [31] . It is far more than that. How much more is the subject of the present paper and we will, without much ado, turn our attention now to the present main task of explaining it in as simple a manor as possible with the only provision which Einstein would have said, “put not more”.
2. An Exact Analytical-Topological Picture of Spacetime
Before reading a single word or equation of the present paper, our advise to the prospective reader is to first have a long contemplative look at Figure 1 and Figure 2 of the present work. The first figure is actually an artist impression of quantum or fractal-Cantorian spacetime (Figure 1). The second is an exact mathematical- topological picture in the sense of the scientific philosophy of people like Wittgenstein (Figure 2). Such a scientific picture is not the product of wild imagination but of stringent application of the dimensional function of von Neumann-Connes’ continuous and noncommutative geometry, namely [71]
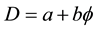 ; and.
; and.
In particular it can be shown that D(O) is the dimensionality of the zero set which models the pre-quantum particle while 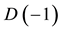 is the dimensionality of the empty set which models the quantum wave. More specifically the pre-quantum particle is accurately represented by the bidimension [64] [71]
is the dimensionality of the empty set which models the quantum wave. More specifically the pre-quantum particle is accurately represented by the bidimension [64] [71]

where D = O is the Menger-Urysohn deductive topological dimension and 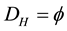 is the corresponding Hausdorff dimension which happens to be the same dimension as that of a triadic Cantor set that is constructed randomly using a uniform distribution. In other words, we could use the follow shorthand notation [64] [71]
is the corresponding Hausdorff dimension which happens to be the same dimension as that of a triadic Cantor set that is constructed randomly using a uniform distribution. In other words, we could use the follow shorthand notation [64] [71]

for the pre-quantum particle and

for the pre-quantum wave. Now using Fibonacci’s growth law and starting with D(O) using (a, b) = (0, 1) and D(1) (a, b) = (1, 0) as said, one obtains for positive dimension the following series
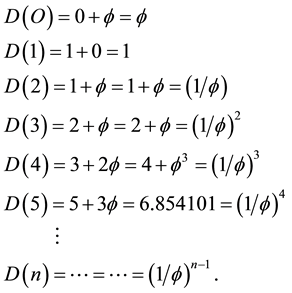
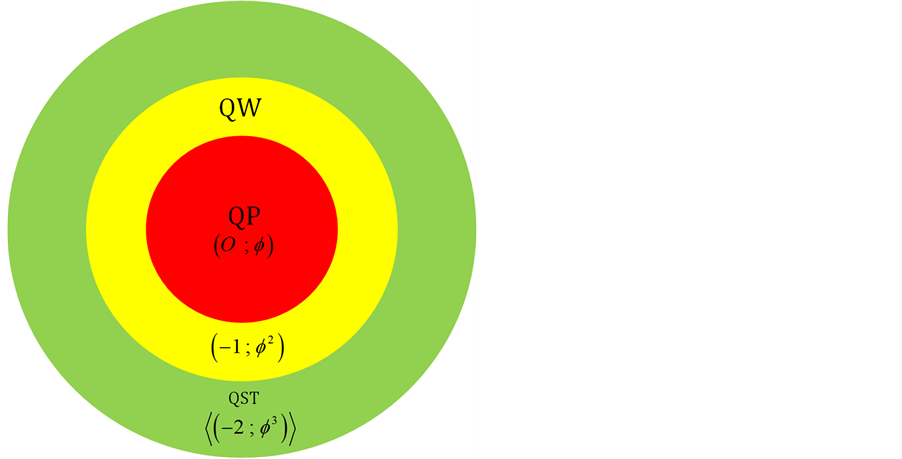
Figure 1. T-duality and Banach-Tarski sphere decomposition Cantorian spacetime of E-infinity theory that is considered here to model our actual spacetime may be envisaged advantageously as in this artist impression. This is basically a two dimensional projection in which each of the larger balls (circles) are a zero set 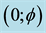 representing the quantum particle while the surface (circumference) represents the empty set
representing the quantum particle while the surface (circumference) represents the empty set 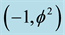 which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set
which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set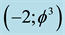 , i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value equal
, i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value equal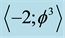 . In other words
. In other words  is our quantum spacetime, which is the cobordism of the quantum wave, which in turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that
is our quantum spacetime, which is the cobordism of the quantum wave, which in turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that 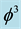 is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime [96] . Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to find first the topological energy density by adding Kaluza-Klein D = 5 to
is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime [96] . Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to find first the topological energy density by adding Kaluza-Klein D = 5 to 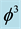 of the spacetime vacuum and find the fractal Kaluza-Klein dimension
of the spacetime vacuum and find the fractal Kaluza-Klein dimension 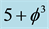 then multiply this with the average Cantorian interval speed of light c =
then multiply this with the average Cantorian interval speed of light c = 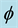
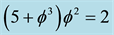
Figure 2. The quantum spacetime E-infinity hierarchy [12] [13] .
Remarkably our Fibonacci-like dimension series could be extended into the negative side using the same logic as follows [64] [71]
Although the preceding computation is mechanistic and essentially elementary, it is quite tedious because of the heavy and slightly confusing notation for negative dimensions. It is at this point that one discovers the advantage of the equivalent notation used in E-infinity theory [69] . The equivalent formula to that of the dimensional function is simply the bijection formula [33] [65] [69]
Here n is the Menger-Urysohn topological dimension while 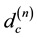
and
correspondingly. For the core Hausdorff dimension of E-infinity we just need to set n = 4 and find [69] - [71]
We note for later use that for n = 2, which means the surface of the pre-quantum wave we find
Now we ask an important question, namely what happens when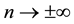
By contrast for 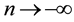
This is clearly the end of our and any universe. Said in a mundane way, we basically have a Cantorian onion in the two dimensional projection as shown in Figure 2. First we have the zero set quantum pre-particle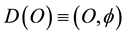


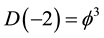
while the average dimension of the entire spacetime is given by
which is precisely the same value as that of the inversion of the cobordism of the empty set quantum wave. Thus we conclude that the picture of Figure 2 is accurate in the most stringent mathematical and transfinite topological sense and we just have to be put 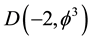
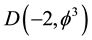
3. The Geometry and Topology of the Casimir Effect [89] [91]
Consider the classical Casimir set up and the hydromechanical analogy that goes with it. Bringing the two Casimir plates as near as a few nano units, we can consider the space between the plates practically totally empty of any “waves” or “particles” pushing them apart. Outside the plates spacetime resembles a stormy sea, which pushes the plates towards each other. Now the inside of the plates has the 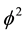
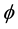
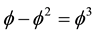
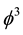
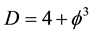
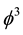
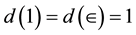
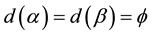
The Casimir energy density is therefore given by the following ratio [35] -[51]
This is nothing but the familiar ordinary energy density of the universe that agrees with all previous analysis of the problem as well as accurate observations and measurements. Now this is only about 4.5 percent of the expected energy, so where is the rest is a natural question. However this question was answered some time ago. The bulk of the energy density is due to the quantum wave and is given by [33] - [51]
This is about 95.5 percent of the energy and is stored in the integer part of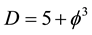
The result is in complete agreement with that obtained using various methods. The fact that this 95.5 percent is located at the edge of the universe is explained within our five dimensional spacetime theory via Dvoretzky’s theorem [59] [63] . On reflection the result is obvious. To see how obvious let us imagine that the two Casimir plates of the famous experiment are taken apart in two opposite directions until each one reaches the cosmological boundary. Thus instead of having 
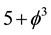
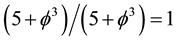
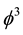

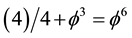
4. The Mirror Symmetry and T-Duality Connecting Casimir Energy with Dark Energy
There is a fascinating history behind the subject of this section testifying to the unity of science and showing that at the end, physicists and mathematicians of all moulds must think and work together on the most fundamental level to be able to push the borders of science forward [95] . The most word economical way to explain mirror symmetry for someone―like the author―living between physics and mathematics, is to say mirror symmetry means that two Calabi-Yau manifolds with different topologies give the same conformal quantum field theory [95] . A more general and probably stronger statement of the same fact can be formulate as a duality which in our particular mirror symmetry case is Witten’s T-duality [93] - [95] .
Let me be more specific even at the risk of appearing elementary or even trivial. Let us start with Hardy’s quantum entanglement. The exact solution for two quantum particles entanglement is given by the well known accurate result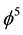
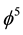

This is an implicit application of T-duality which is clear cut and in view of the experimental verification of Hardy’s entanglement and the theoretical success of M-theory points clearly to being a physical reality [9] [12] [15] [30] [94] . It is really hard to believe that all these results, pertinent to the dark energy density of the cosmos 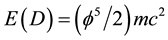
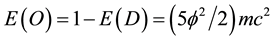
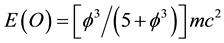
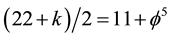
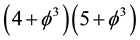
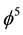
5. Conclusions
To put things into perspective we should not forget that we always referred to the Casimir effect and dark energy as different forms of quantum vacuum zero point fluctuation. Nevertheless the fact that 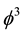
It consists of three main layers [41] -[45] . We have first an infinite number of zero and empty sets with an average bi-dimension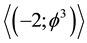
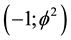
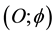
Acknowledgements
For a young man who said more than half a century ago “never trust anyone above thirty”, to become himself over seventy it is a time to pause and thank all those who really fundamentally influenced him and helped him in so many ways that he feels today grateful to them. On the top of the list his father, Major General Salah El Naschie (Alnashaee), then his teacher and friends, Prof. Dr. Alf Pflüger, Prof. T. Lehmann, Prof. E. Stein, Prof. R. Deboer, Prof. J.M.T. Thompson, Prof. T. Barta, Prof. Sir Herman Bondi, Prof. W. Martienssen, Prof. W. Greiner and Prof. IlyaPigogine. Last but not least, working with His Excellency Prof. Salah Al Athel of Saudi Arabia was one of the most important scientific experiences in the author’s life. There are of course many other names which the fading memory of an old man is not helping to remember but to all of them, I am truly indebted.
Cite this paper
M. S.El Naschie, (2015) Hubble Scale Dark Energy Meets Nano Scale Casimir Energy and the Rational of Their T-Duality and Mirror Symmetry Equivalence. World Journal of Nano Science and Engineering,05,57-67. doi: 10.4236/wjnse.2015.53008
References
- 1. Bondi, S.H. (1964) Relativity and the Commonsense. A New Approach to Einstein. Heinemann, London.
- 2. Rindler, W. (2004) Relativity (Special, General and Cosmological). Oxford University Press, Oxford.
- 3. Okun, L.B. (2009) Energy and Mass in Relativity Theory. World Scientific, Singapore.
- 4. Rindler, W. (1991) Introduction to Special Relativity. Oxford Science Publications, Oxford.
- 5. El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic ‘t Hooft-Veltman-Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221.
http://dx.doi.org/10.4236/wjnst.2014.44027 - 6. Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145.
http://dx.doi.org/10.4236/ojm.2013.34020 - 7. Marek-Crnjac, L. and He, J.-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471.
http://dx.doi.org/10.4236/ijaa.2013.34053 - 8. Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436.
http://dx.doi.org/10.4236/jmp.2014.515144 - 9. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
http://dx.doi.org/10.4236/jqis.2011.12007 - 10. El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26.
http://dx.doi.org/10.4236/jqis.2013.31006 - 11. El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54.
http://dx.doi.org/10.4236/ijmnta.2013.21005 - 12. El Naschie, M.S. (2013) Quantum Entanglement: Where Dark Energy and Negative Gravity plus Accelerated Expansion of the Universe Comes From. Journal of Quantum Information Science, 3, 57-77.
http://dx.doi.org/10.4236/jqis.2013.32011 - 13. El Naschie, M.S. (2013) A Fractal Menger Sponge Space-Time Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy. International Journal of Modern Nonlinear Theory and Application, 2, 107-121.
http://dx.doi.org/10.4236/ijmnta.2013.22014 - 14. El Naschie, M.S. (2013) The Hydrogen Atom Fractal Spectra, the Missing Dark Energy of the Cosmos and Their Hardy Quantum Entanglement. International Journal of Modern Nonlinear Theory and Application, 2, 167-169.
http://dx.doi.org/10.4236/ijmnta.2013.23023 - 15. El Naschie, M.S. (2013) A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy. International Journal of Astronomy and Astrophysics, 3, 483-493.
http://dx.doi.org/10.4236/ijaa.2013.34056 - 16. El Naschie, M.S. (2013) What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy and Astrophysics, 3, 205-211.
http://dx.doi.org/10.4236/ijaa.2013.33024 - 17. El Naschie, M.S. (2013) The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling of the Planck Scale. Open Journal of Microphysics, 3, 64-70.
http://dx.doi.org/10.4236/ojm.2013.33012 - 18. El Naschie, M.S. (2013) From Yang-Mills Photon in Curved Spacetime to Dark Energy Density. Journal of Quantum Information Science, 3, 121-126.
http://dx.doi.org/10.4236/jqis.2013.34016 - 19. El Naschie, M.S. (2014) Calculating the Exact Experimental Density of the Dark Energy in the Cosmos Assuming a Fractal Speed of Light. International Journal of Modern Nonlinear Theory and Application, 3, 1-5.
http://dx.doi.org/10.4236/ijmnta.2014.31001 - 20. El Naschie, M.S. (2014) Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity. World Journal of Mechanics, 4, 153-156.
http://dx.doi.org/10.4236/wjm.2014.46017 - 21. El Naschie, M.S. (2014) Capillary Surface Energy Elucidation of the Cosmic Dark Energy—Ordinary Energy Duality. Open Journal of Fluid Dynamics, 4, 15-17.
http://dx.doi.org/10.4236/ojfd.2014.41002 - 22. El Naschie, M.S. (2014) Einstein’s General Relativity and Pure Gravity in a Cosserat and De Sitter-Witten Spacetime Setting as the Explanation of Dark Energy and Cosmic Accelerated Expansion. International Journal of Astronomy and Astrophysics, 4, 332-339.
http://dx.doi.org/10.4236/ijaa.2014.42027 - 23. El Naschie, M.S. (2014) Electromagnetic—Pure Gravity Connection via Hardy’s Quantum Entanglement. Journal of Electromagnetic Analysis and Applications, 6, 233-237.
http://dx.doi.org/10.4236/jemaa.2014.69023 - 24. El Naschie, M.S. (2014) Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91.
http://dx.doi.org/10.4236/jqis.2014.42008 - 25. El Naschie, M.S. (2014) Entanglement of E8E8 Exceptional Lie Symmetry Group Dark Energy, Einstein’s Maximal Total Energy and the Hartle-Hawking No Boundary Proposal as the Explanation for Dark Energy. World Journal of Condensed Matter Physics, 4, 74-77.
http://dx.doi.org/10.4236/wjcmp.2014.42011 - 26. El Naschie, M.S. (2014) The Meta Energy of Dark Energy. Open Journal of Philosophy, 4, 157-159.
http://dx.doi.org/10.4236/ojpp.2014.42022 - 27. El Naschie, M.S. (2014) Pinched Material Einstein Space-Time Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90.
http://dx.doi.org/10.4236/ijaa.2014.41009 - 28. El Naschie, M.S. (2014) From Chern-Simon, Holography and Scale Relativity to Dark Energy. Journal of Applied Mathematics and Physics, 2, 634-638.
http://dx.doi.org/10.4236/jamp.2014.27069 - 29. El Naschie, M.S. (2014) Why E Is Not Equal to mc2. Journal of Modern Physics, 5, 743-750.
http://dx.doi.org/10.4236/jmp.2014.59084 - 30. El Naschie, M.S. (2013) Nash Embedding of Witten’s M-Theory and the Hawking-Hartle Quantum Wave of Dark Energy. Journal of Modern Physics, 4, 1417-1428.
http://dx.doi.org/10.4236/jmp.2013.410170 - 31. El Naschie, M.S. (2013) Dark Energy from Kaluza-Klein Spacetime and Noether’s Theorem via Lagrangian Multiplier Method. Journal of Modern Physics, 4, 757-760.
http://dx.doi.org/10.4236/jmp.2013.46103 - 32. El Naschie, M.S. (2013) The hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy. Journal of Modern Physics, 4, 354-356.
http://dx.doi.org/10.4236/jmp.2013.43049 - 33. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 34. El Naschie, M.S. (2014) From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
http://dx.doi.org/10.4236/jamp.2014.28088 - 35. He, J.H. and Marek-Crnjac, L. (2013) Mohamed El Naschie’s Revision of Albert Einstein’s E = m0c2: A Definite Resolution of the Mystery of the Missing Dark Energy of the Cosmos. International Journal of Modern Nonlinear Theory and Application, 2, 55-59.
http://dx.doi.org/10.4236/ijmnta.2013.21006 - 36. El Naschie, M.S. and Marek-Crnjac, L. (2012) Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity. International Journal of Modern Nonlinear Theory and Application, 1, 118-124.
http://dx.doi.org/10.4236/ijmnta.2012.14018 - 37. El Naschie, M.S. and Helal, A. (2013) Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343.
http://dx.doi.org/10.4236/ijaa.2013.33037 - 38. Marek-Crnjac, L. and El Naschie, M.S. (2013) Chaotic Fractal Tiling for the Missing Dark Energy and Veneziano Model. Applied Mathematics, 4, 22-29.
http://dx.doi.org/10.4236/am.2013.411A2005 - 39. Marek-Crnjac, L. and El Naschie, M.S. (2013) Quantum Gravity and Dark Energy Using Fractal Planck Scaling. Journal of Modern Physics, 4, 31-38.
http://dx.doi.org/10.4236/jmp.2013.411A1005 - 40. Auffray, J.P. (2015) E Infinity, the Zero Set, Absolute Space and Photon Spin. Journal of Modern Physics, 6, 536-545.
http://dx.doi.org/10.4236/jmp.2015.65058 - 41. El Naschie, M.S., Olsen, S., He, J.H., Nada, S., Marek-Crnjac, L. and Helal, A. (2012) On the Need for Fractal Logic in High Energy Quantum Physics. International Journal of Modern Nonlinear Theory and Application, 1, 84-92.
http://dx.doi.org/10.4236/ijmnta.2012.13012 - 42. El Naschie, M.S., Marek-Crnjac, L., Helal, A.M. and He, J.-H. (2014) A Topological Magueijo-Smolin Varying Speed of Light Theory, the Accelerated Cosmic Expansion and the Dark Energy of Pure Gravity. Applied Mathematics, 5, 1780-1790.
http://dx.doi.org/10.4236/am.2014.512171 - 43. El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and “tHooft”s 4-e Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37.
http://dx.doi.org/10.11648/j.ajaa.20140203.12 - 44. El Naschie, M.S. (2014) Hardy’s Entanglement as the Ultimate Explanation for the Observed Cosmic Dark Energy and Accelerated Expansion. International Journal of High Energy Physics, 1, 13-17.
http://dx.doi.org/10.11648/j.ijhep.20140102.11 - 45. El Naschie, M.S. (2014) Deriving E = mc2/22 of Einstein’s Ordinary Quantum Relativity Energy Density from the Lie Symmetry Group SO (10) of Grand Unification of All Fundamental Forces and without Quantum Mechanics. American Journal of Mechanics & Applications, 2, 6-9.
http://dx.doi.org/10.11648/j.ajma.20140202.11 - 46. El Naschie, M.S. (2014) Cosserat-Cartan Modification of Einstein-Riemann Relativity and Cosmic Dark Energy Density. American Journal of Modern Physics, 3, 82-87.
http://dx.doi.org/10.11648/j.ajmp.20140302.17 - 47. El Naschie, M.S. (2014) Asymptotically Safe Pure Gravity as the Source of Dark Energy of the Vacuum. International Journal of Astrophysics & Space Science, 2, 12-15.
http://dx.doi.org/10.11648/j.ijass.20140201.13 - 48. El Naschie, M.S. (2014) Logarithmic Running of ‘t Hooft-Polyakov Monopole to Dark Energy. International Journal of High Energy Physics, 1, 1-5.
http://dx.doi.org/10.11648/j.ijhep.20140101.11 - 49. El Naschie, M.S. (2013) Experimentally Based Theoretical Arguments That Unruh’s Temperature, Hawking’s Vacuum Fluctuation and Rindler’s Wedge Are Physically Real. American Journal of Modern Physics, 2, 357-361.
http://dx.doi.org/10.11648/j.ajmp.20130206.23 - 50. Marek-Crnjac, L. (2013) Modification of Einstein’s E = mc2 to E = 1/22 mc2. American Journal of Modern Physics, 2, 255-263.
http://dx.doi.org/10.11648/j.ajmp.20130205.14 - 51. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.
http://dx.doi.org/10.1134/S0202289313030031 - 52. El Naschie, M.S. (2013) Determining the Missing Dark Energy Density of the Cosmos from a Light Cone Exact Relativistic Analysis. Journal of Physics, 2, 19-25.
- 53. El Naschie, M.S. (2013) The Quantum Entanglement behind the Missing Dark Energy. Journal of Modern Physics and Applications, 2, 88-96.
- 54. El Naschie, M.S. (2014) Dark Energy via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
- 55. El Naschie, M.S. (2014) Rindler Space Derivation of Dark Energy. Journal of Modern Physics and Applications, 6, 1-10.
- 56. Tang, W., et al. (2014) From Nonlocal Elasticity to Nonlocal Spacetime and Nano Science. Bubbfil Nanotechnology, 1, 3-12.
- 57. El Naschie, M.S. (2014) To Dark Energy Theory from a Cosserat-Like Model of Spacetime. Problems of Nonlinear Analysis in Engineering Systems, 20, 79-98.
- 58. El Naschie, M.S. (2012) Revising Einstein’s E = mc2. A Theoretical Resolution of the Mystery of Dark Energy. Proceedings of the 4th Arab International Conference in Physics and Material Science, Egypt, 1-30 October 2012, 1.
- 59. Ball, K.M. (1991) Volume Ratios and a Reverse Isoperimetric Inequality. Journal of London Mathematical Society, 44, 351-359.
http://dx.doi.org/10.1112/jlms/s2-44.2.351 - 60. Pisier, G. (1989) The Volume of Convex Bodies and Banach Space Geometry. Tracts in Math 94, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511662454 - 61. Kasin, B.S. (1977) The Width of Certain Finite-Dimensional Sets and Classes of Smooth Functions. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 41, 334-351. (In Russian)
- 62. Guedon, O. (2013) Concentration Phenomena in High Dimensional Geometry. arXiv:1310.1204V1 [math.FA].
- 63. He, J.-H. (Guest Editor) (2013) Special Issue on Recent Developments on Dark Energy and Dark Matter. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 3, 1-62.
- 64. He, J.-H. and El Naschie, M.S. (2012) On the Monadic Nature of Quantum Gravity as a Highly Structured Golden Ring, Spaces and Spectra. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 94-98.
- 65. El Naschie, M.S. (2012) Towards a General Transfinite Set Theory for Quantum Mechanics. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 135-142.
- 66. El Naschie, M.S., He, J.-H., Nada, S., Marek-Crnjac, L. and Helal, M. (2012) Golden Mean Computer for High Energy Physics. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 80-92.
- 67. El Naschie, M.S. (2012) The Minus One Connection of Relativity, Quantum Mechanics and Set Theory. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 131-134.
- 68. El Naschie, M.S. Dark Energy and Its Cosmic Density from Einstein’s Relativity and Gauge Fields Renormalization Leading to the Possibility of a New ‘tHooft Quasi Particle. The Open Journal of Astronomy, in Press.
- 69. El Naschie, M.S. (2004) A Review of E Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 70. El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646.
http://dx.doi.org/10.1016/j.chaos.2008.09.059 - 71. Connes, A. (1994) Noncommutative Geometry. Academic Press, San Diego.
- 72. Krantz, S.G. and Parks, H.R. (2008) Geometric Integration Theory. Birkhauser, Boston.
http://dx.doi.org/10.1007/978-0-8176-4679-0 - 73. El Naschie, M.S. (1997) Remarks on Super Strings, Fractal Gravity, Nagasawa’s Diffusion and Cantorian Spacetime. Chaos, Solitons & Fractals, 8, 1873-1886.
http://dx.doi.org/10.1016/S0960-0779(97)00124-0 - 74. El Naschie, M.S. (1997) Introduction to Nonlinear Dynamics, General Relativity and the Quantum—The Uneven Flow of Fractal Time. Chaos, Solitons & Fractals, 8, vii-x.
http://dx.doi.org/10.1016/S0960-0779(97)88695-X - 75. El Naschie, M.S. (1999) Hyper-Dimensional Geometry and the Nature of Physical Spacetime. Chaos, Solitons & Fractals, 10, 155-158.
http://dx.doi.org/10.1016/S0960-0779(98)00235-5 - 76. El Naschie, M.S. E Infinity—High Energy Communications Nos. 1 to 90. April 2010 to December 2012.
- 77. Chen, N.X. (2010) Mobius Inversion in Physics. World Scientific, Singapore.
- 78. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.
http://dx.doi.org/10.1007/s10773-014-2123-8 - 79. El Naschie, M.S. (2001) On Twistors in Cantorian E Infinity Space. Chaos, Solitons & Fractals, 12, 741-746.
http://dx.doi.org/10.1016/S0960-0779(00)00193-4 - 80. Rossler, O.E. (1998) Endophysics. World Scientific, Singapore.
http://dx.doi.org/10.1142/3183 - 81. El Naschie, M.S. (2001) On a General Theory for Quantum Gravity. In: Diebner, H., Druckrey, T. and Weibel, P., Eds., Science of the Interface, Genista Verlag, Tübingen.
- 82. Li, M. (2004) A Model of Holographic Dark Energy. Physics Letters B, 603, 1-5.
http://dx.doi.org/10.1016/j.physletb.2004.10.014 - 83. El Naschie, M.S. (2006) Holographic Dimensional Reduction. Center Manifold Theorem and E Infinity. Chaos, Solitons & Fractals, 29, 816-822.
http://dx.doi.org/10.1016/j.chaos.2006.01.013 - 84. Balachandran, A.P., Kürkcüoglu, S. and Vaidya, S. (2007) Lectures on Fuzzy and Fuzzy Susy Physics. World Scientific, Singapore.
- 85. Bahcall, J., Piran, T. and Weinberg, S. (2004) Dark Matter in the Universe. World Scientific, Singapore.
- 86. Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observations. Cambridge University Press, Cambridge.
- 87. Ruiz-Lapuente, P. (2010) Dark Energy, Observational and Theoretical Approaches. Cambridge University Press, Cam- bridge.
- 88. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entangled Origin. Journal of Quantum Information Science, 4, 284-291.
http://dx.doi.org/10.4236/jqis.2014.44023 - 89. El Naschie, M.S. (2014) Casimir-Like Energy as a Double Eigenvalue of Quantumly Entangled System Leading to the Missing Dark Energy Density of the Cosmos. International Journal of High Energy Physics, 1, 55-63.
http://dx.doi.org/10.11648/j.ijhep.20140105.11 - 90. Perlmutter, S., et al. (1999) Supernova Cosmology Project Collaboration: Measurements of Ω and Λ from 42 High Redshift Supernova. Astrophysics Journal, 517, 565-585.
http://dx.doi.org/10.1086/307221 - 91. El Naschie, M.S. (2015) On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nano- tech Reactor Proposal. Open Journal of Applied Science, in Press.
- 92. Kodiyalam, V. and Sunder, V.S. (2001) Topological Quantum Field Theories from Subfactors. Chapman & Hall/CRC, London.
- 93. El Naschie, M.S. (2005) A Few Hints and Some Theorem about Witten’s M Theory and T-Duality. Chaos, Solitons & Fractals, 25, 545-548.
http://dx.doi.org/10.1016/j.chaos.2005.01.009 - 94. Marek-Crnjac, L., El Naschie, M.S. and He, J.-H. (2013) Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology. International Journal of Modern Nonlinear Theory and Application, 2, 78-88.
http://dx.doi.org/10.4236/ijmnta.2013.21A010 - 95. Yau, S.T. and Nadis, S. (2010) The Shape of Inner Space. Basic Book, Persens Group, New York.
- 96. Bell, J.S. (1991) Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge.
- 97. Penrose, R. (2004) The Road to Reality. A Complete Guide to the Laws of the Universe. Jonathan Cape, London.
NOTES
*Dedicated to the memory of Sir Herman Bondi and Prof. Thomas Barta―two very memorable teachers and fatherly friends.