Journal of Sensor Technology
Vol.05 No.04(2015), Article ID:62241,8 pages
10.4236/jst.2015.54008
Nondestructive Determination of Moisture Content in Dry Fruits by Impedance and Phase Angle Measurements
Chari V. Kandala1, Ron Holser2, Jaya Sundaram3, Naveen Puppala4
1National Peanut Research Laboratory, USDA, Dawson, GA, USA
2Russell Research Center, USDA, Athens, GA, USA
3Faculty of Engineering, University of Georgia, Athens, GA, USA
4Clovis Center, New Mexico State University, Clovis, NM, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 December 2015; accepted 21 December 2015; published 25 December 2015
ABSTRACT
An electronic method to estimate the moisture content (MC) of dry fruits by measuring the impedance (Z) and phase angle (θ) of a cylindrical parallel-plate capacitor with dry fruit sample between the plates, using a CI meter (Chari’s Impedance meter) at 1 and 9 MHz is described. Capacitance C was derived from Z and θ, and using the C, θ, and Z values of a set of dried cherries, whose MC values were later determined by the vacuum hot air-oven method, a calibration equation was developed. Using this equation, and their measured C, θ, and Z values, the MC of a group of cherries, not used in the calibration, was predicted. The predicted values were compared with their air-oven values. Similar predictions were done using the same method on dried blueberries. The method worked well with a good R2 value, and showed a low standard error of prediction (SEP) in the measured MC range between 5% and 30% for cherries, and 9% and 22% for blueberries.
Keywords:
Cherries, Blueberries, CI Meter, Moisture Content, Capacitance, Impedance, Dry Fruits

1. Introduction
Dry fruit is fruit from which the majority of the original moisture content (MC) has been removed either naturally, or through the use of hot air dryers or dehydrators. Dried fruit has a long tradition of use dating back to the fourth millennium BC [1] , and is prized because of its sweet taste, nutritive values, and long shelf life [2] . Drying the fruits, to MC values below 10% from the incoming produce originally having about 40% moisture, facilitates extending their shelf life considerably. United States is the second largest producer of cherries in the world, and has a thriving export market for dry fruits such as cherries and blueberries. Dried fruits retain most of the nutritional values of fresh fruit. Dried fruits and nuts are antioxidants. Dried fruits occupy less storage space than the fresh ones, and it is easy to take them along for consumption. Dried fruits are a great snack, being convenient and easy to pack no matter what the season or activity. Dried fruits can also be added to granola or hot cereals, salads, pilafs, meat dishes and much more. Cherries, strawberries and blueberries are infused with a sweetener such as sucrose syrup before drying. Drying of cherries is done by atmospheric forced-air dryers. During the drying process the MC has to be measured several times to make sure the required MC levels are achieved, and to stop the heating at the right time. Overheating increases the costs, and may affect the quality of the fruit. Drying with hot air at controlled humidity has minimal effect on the nutritional value. Presently used method for MC determination is, either by vacuum-oven method [3] , or by Karl Fisher titration [4] . Both methods are time consuming and destructive. An electronic method is described here for the rapid and nondestructive measurement of the MC of dry fruits from the measurement of impedance and phase angle of a parallel- plate capacitance, holding about 100 g of the fruit sample between the plates. This method is rapid and nondestructive. No sample preparation is needed as in the other two methods. The method worked successfully for cherries and blueberries, and can be extended to other types of fruits such as raspberries.
2. Materials and Methods
2.1. Basic Principles
The capacitance of a parallel-plate capacitor with plate area A and plate separation d, filled with a dielectric material, at a frequency f1 is given by:
 (1)
(1)
and at a frequency f2 is given by:
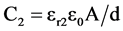 (2)
(2)
εr1 and εr2 are the dielectric constants of the dielectric material at the two frequencies and ε0 is the permittivity of free space (8.854 × 10−12 farad/m). Using these two equations we can write the difference in the dielectric constants as:
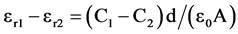 (3)
(3)
It was earlier found that (C1 − C2) was a good estimate of the moisture content, but it was highly influenced by the size and shape of the peanut kernels [5] . Two other electrical parameters, dissipation factor D, and phase angle θ were also measured at the two frequencies, 1 and 4.5 MHz, and the differences in the values of these two parameters at the two frequencies, (D1 − D2) and (θ1 − θ2) were incorporated into an empirical equation, along with (C1 − C2), from which the moisture content of single peanut kernels were calculated. Capacitance, phase angle and dissipation factor were measured on single kernels with each kernel between, and in contact with the two parallel plates at the two frequencies, 1 and 4.5 MHz, and the differences in the values of C, θ, and D were used in an empirical equation, to calculate the MC of the peanut sample placed between the plates. This method was extended to dry fruits and tested on dry fruits with an instrument called the CI meter (Chari’s Impedance meter) designed at the USDA laboratories [6] . Dry cherries were placed between the parallel-plates as done with the peanuts, and the variation in impedance, (Z1 − Z2) and phase angle (θ1 − θ2) at 1 MHz and 5 MHz were measured. The capacitance value at each frequency was calculated from the equation:
 (4)
(4)
where  sin θ, the imaginary part of the impedance. The value of (C1 − C2) was computed and used along with (Z1 − Z2), and (θ1 − θ2) in an empirical equation to determine the MC of a single or a small quantity (five to seven) of cherry samples placed between the plates. The method worked satisfactorily. However, for the dry fruit industry it would be more useful to rapidly and nondestructively determine the MC of larger samples of dry fruits, say about 100 to 150 g. The sample holder was modified for this purpose and the signals were suitably enhanced to traverse the longer distance between the two parallel-plate electrodes that were embedded in a non-conducting cylinder holding the fruit samples. Using the CI meter, the values of impedance Z, and phase angle θ were measured at 1 and 9 MHz, and the corresponding capacitance values were computed from Equation (4) for each sample. The variation in capacitance, impedance and phase angle with moisture content for dry fruits was substantial at 1MHz and 9MHz, and thus measurements were made at these two frequencies. An empirical equation was developed that has terms (C1 − C2), (Z1 − Z2), and (θ1 − θ2) where, C1, Z1, θ1 and C2, Z2, θ2 are the measured values of capacitance, impedance and phase angle at 1 and 9 MHz. From the empirical equation, the MC of the dry fruit sample was obtained. The phase angle change, (θ1 − θ2) accounts for the loss factor. Dissipation factor is a measure of energy loss that results from subjecting a dielectric to an alternating current electric field. It is related to the Q factor of the material under test and is a measure of the energy stored in the electric field relative to energy dissipated in any one period. The power dissipated depends on the equivalent resistance of the complex circuit, and thus the variation in the impedance values, (Z1 − Z2) of the system at the two frequencies adequately represents the term (D1 − D2), and was used to replace (D1 − D2). Thus, from the values of (C1 − C2), (θ1 − θ2) and (Z1 − Z2), measured with a two parallel-plate system fitted inside a cylinder, the MC of the grain, nuts or any other aqueous sample could be estimated to an acceptable accuracy [7] . For a single parallel-plate system the semi-empirical equation used was:
sin θ, the imaginary part of the impedance. The value of (C1 − C2) was computed and used along with (Z1 − Z2), and (θ1 − θ2) in an empirical equation to determine the MC of a single or a small quantity (five to seven) of cherry samples placed between the plates. The method worked satisfactorily. However, for the dry fruit industry it would be more useful to rapidly and nondestructively determine the MC of larger samples of dry fruits, say about 100 to 150 g. The sample holder was modified for this purpose and the signals were suitably enhanced to traverse the longer distance between the two parallel-plate electrodes that were embedded in a non-conducting cylinder holding the fruit samples. Using the CI meter, the values of impedance Z, and phase angle θ were measured at 1 and 9 MHz, and the corresponding capacitance values were computed from Equation (4) for each sample. The variation in capacitance, impedance and phase angle with moisture content for dry fruits was substantial at 1MHz and 9MHz, and thus measurements were made at these two frequencies. An empirical equation was developed that has terms (C1 − C2), (Z1 − Z2), and (θ1 − θ2) where, C1, Z1, θ1 and C2, Z2, θ2 are the measured values of capacitance, impedance and phase angle at 1 and 9 MHz. From the empirical equation, the MC of the dry fruit sample was obtained. The phase angle change, (θ1 − θ2) accounts for the loss factor. Dissipation factor is a measure of energy loss that results from subjecting a dielectric to an alternating current electric field. It is related to the Q factor of the material under test and is a measure of the energy stored in the electric field relative to energy dissipated in any one period. The power dissipated depends on the equivalent resistance of the complex circuit, and thus the variation in the impedance values, (Z1 − Z2) of the system at the two frequencies adequately represents the term (D1 − D2), and was used to replace (D1 − D2). Thus, from the values of (C1 − C2), (θ1 − θ2) and (Z1 − Z2), measured with a two parallel-plate system fitted inside a cylinder, the MC of the grain, nuts or any other aqueous sample could be estimated to an acceptable accuracy [7] . For a single parallel-plate system the semi-empirical equation used was:
 (5)
(5)
 are the calibration constants obtained by regression analysis done on the measured values of C, θ, and Z of several samples of known MC values (determined by the standard-oven method).
are the calibration constants obtained by regression analysis done on the measured values of C, θ, and Z of several samples of known MC values (determined by the standard-oven method).
2.2. Moisture Meter and Electrode System
The electronic circuit of the CI meter developed by the first author was well described earlier [8] . Three frequencies, 1, 5, and 9 MHz were generated using crystal oscillators. These signals were applied alternately to the fruit samples held between two parallel-plate electrodes fixed in a cylinder (Figure 1), made of a non-conduct- ing material. The original signal and the signal coming out of the sample were measured as er and em at each frequency, and the impedance Z, proportional to the ratio of these two values, was calculated at each frequency. Feeding these two signals into a phase detector, the phase angle θ between them was determined at the three frequencies.
The capacitance of the system at each frequency was computed as:
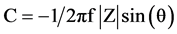 (6)
(6)
Figure 1. CI meter set up for MC measurement of dry fruits. 1 Cylinder holding dry Cherries; 2 Box with shelf for collecting samples; 3 Chari’s Meter; 4 Analog to Digital Interface; 5 Lap top for data acquisition.
Two rectangular aluminum plates 40 mm wide and 60 mm long constitute the electrode system. The electrodes were embedded in the walls of a cylinder with an outer diameter of 60 mm and a length of 80 mm, made of an acrylic material. Thus, the electrodes cover the entire length of the cylinder except for 10 mm at the top and the bottom. The sample when placed in the cylinder occupies the space between the two electrodes. The parallel-plate system is connected to the CI meter as shown in Figure 1. The cylinder sits on an acrylic box fitted with a drawer. With the drawer pushed inside, the sample stays in the cylinder and when the drawer is pulled out the sample drops into the box. A lap-top computer was used to control and collect data from the CI meter.
2.3. Dry Fruit Samples
Cherries dried to seven moisture levels, ranging between 8% and 30% were obtained from Oceana Foods1, Shelby, Michigan. They were put in seven air-tight containers and allowed to equilibrate in a cold storage at 4˚C for several days, rotating the samples periodically. The MC value2 the cherries in each container was determined by the vacuum-oven method. Three replicates were used for each MC level. The samples from each level were divided into two groups, and measurements were made on seven calibration and seven validation sets. The validation set have the same MC values of 8.23%, 10.12%, 14.22%, 18.32%, 22.23%, 26.33% and 30% as the calibration set but were not the same that were used in the calibration.
Blueberries dried to four different moisture levels were also obtained from Oceana Foods, and were placed in four air-tight containers and allowed to equilibrate in a cold storage at 4˚C for several days, rotating the samples periodically, as done for the cherries. Three replicate samples from each bottle were then used to determine their MC by the standard vacuum-oven method for dry fruits [3] . In this method, the three replicates at each moisture level were weighed and their wet weights were recorded. The samples were then placed in a vacuum- oven at 70˚C ± 1˚C for 6 h under a pressure of 100 mm Hg. After drying, the samples were removed from the oven, allowed to reach room temperature, and their dry weights were taken. The % MC of the samples was determined as: (wet weight-dry weight) × 100/(wet weight). Thus four MC levels of 9.82%, 10.11%, 14.07% and 21.53% of blueberries were obtained for calibration and validation. The samples from each of these four moisture levels were split into two groups, and stored separately. The first group of samples was used for calibration, and the second group for validation. Thus, though both the calibration and validation groups are of the same MC values, the samples used for validation are not the same as used for the calibration.
2.4. Measurements
Measurements were first made on the cherry samples. All cherry samples were brought to room temperature before the CI meter measurements were made on them. With the drawer of the sample collection box pushed inside, cherries from the 8.23% calibration group were dropped into the cylindrical electrode system filling it up to the top. The cylinder accommodates about 100 g of cherries. Three measurements of impedance Z, and phase angle θ were made on this sample using the CI meter, and the values were recorded on the lap-top. The drawer is pulled out and the samples were removed from the cylinder. Measurements were repeated on another nine samples from the 8.23% moisture group. Similar measurements were done on 10 samples from the six other moisture levels in the calibration group, and 10 samples each from the seven moisture levels from the validation group. Similarly, measurements were repeated on 10 samples each from the four moisture levels of the calibration, and four moisture levels of the validation groups of blueberries.
2.5. Data Analysis
The measured values of Z and θ and the derived values of C, at 1 and 9 MHz only, were used for calibration and prediction of MC of both cherries and blueberries. For cherries, the data on the seven calibration lots along with their vacuum-oven MC values was analyzed using multi linear regression analysis software package, Unscrambler [9] . A calibration equation was developed using terms (C1 − C2), (θ1 − θ2), and (Z1 − Z2) and their square terms. Using this equation the MC values of the validation group were predicted, and compared with their vacuum-oven values. The fitness of the calibration equation was assessed from the associated statistical parameters.
In the case of blueberries as the data available was limited to four moisture levels each for calibration and prediction, the statistical package SAS [10] was used to obtain the regression equation using similar terms as used for cherries. From this equation, the MC values of the samples from the validation group were predicted, and compared with their vacuum-oven values.
3. Results and Discussion
Shown in Table 1 are the MC values obtained from the Unsrambler analysis on the seven calibration lots using the C, θ, and Z values measured by the CI meter. Also given are the MC values obtained with the vacuum-oven method, the standard deviation and the difference between the vacuum-oven value and the CI meter predicted value. Shown in Table 2 are the fitness measures for the calibration model developed with the measured parameters Z and θ, and the computed parameter C of the seven moisture levels of the calibration group of cherries. An R2 (squared correlation coefficient) of 0.98, and a standard error of calibration (SEC)3 of 0.99, and a low RMSEC (root mean square error of calibration) show that the model is quite suitable for prediction of MC of cherries by this method. Shown in Table 3 below are the predicted values using the calibration model of the seven validation groups of cherries. As indicated before, these cherry samples are not the same ones used in the calibration, though they have the same MC values. Also given are their standard vacuum-oven values, the difference between the predicted and standard values, and the standard deviations for each moisture level.
Shown in Table 4 are the fitness measures for the validation model developed with the measured parameters Z and θ, and the computed parameter C of the seven moisture levels of the validation group of cherries. The differences between the CI meter and the oven values are less than 1% at all the moisture levels except the 14.22%, where it is 1.12%. Even in the calibration group the difference at this moisture level was 0.95%. This probably could be the result of non-homogeneity of the samples in this level. The fitness measures of the validation group are shown in Table 4. Given are the R2, RMSEP (root mean square error of prediction) and SEP4 (standard error of prediction). An R2 value of 0.97 and a SEP of 1.10 are quite compatible with the R2 and SEC values of the calibration group indicating the suitability of the model for the prediction of MC of dry cherries in the range of 8% to 30% by the CI meter. Shown in Figure 2 are the CI meter values plotted against the vacuum-oven values for all the 70 samples measured from the validation groups. A good correlation, within the permissible limits, in the prediction of MC with the CI meter could be seen, taking into consideration of the measurements of all the seven moisture levels from 8% to 30%.
Similarly for blueberries, from the measured values of Z and θ, the capacitance values C were computed using Equation (7), for the four moisture levels each in the calibration and validation groups. The Z, θ, C values of each sample (10 samples in each moisture level and a total of 40 samples) from the calibration group, along with the corresponding oven determined MC value, were subjected to SAS procedures for regression analysis to determine the constants A0 to A6 in Equation (5). Substituting the values of the constants in Equation (5) we get the prediction equation for blueberries as:
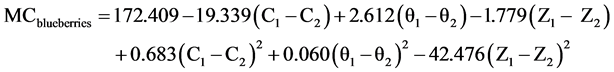 (7)
(7)
Substituting the measured values of C, θ and Z at the two frequencies in Equation (7) the calculated values of MC of the four moisture levels of the calibration group are shown in Table 5 below. Also shown are the standard deviations, and the difference between the oven and CI meter values. The regression had an R2 value of 0.98 and an SEC of 0.63. These parameters indicate that Equation (7) is suitable for prediction of MC by the CI meter. To confirm this, from the measurements on the four validation sets, the MC of each sample was determined
Table 1. Comparison of mean MC values determined by vacuum-oven and CI meter methods for the calibration group of cherries (Average of 10 samples in each moisture group).
Table 2. Fitness measures for the calibration group of cherries.
Table 3. Comparison of mean MC values determined by vacuum-oven and CI meter methods for the validation group of cherries (Average of 10 samples in each moisture group).
Table 4. Fitness measures for the validation group of cherries.
Table 5. Comparison of mean MC values determined by vacuum-oven and CI meter methods for the calibration group of blueberries (Average of 10 samples in each moisture group).
Table 6. Comparison of mean MC values determined by vacuum-oven and CI meter methods for the validation group of blueberries (Average of 10 samples in each moisture group).
Figure 2. CI meter values plotted against the standard vacuum-oven values for the validation group of cherries (All 70 samples).
Figure 3. CI meter values plotted against the standard vacuum-oven values for the validation group of blueberries (all 40 samples).
using Equation (7), averaged over the 10 samples in each moisture group, and compared with the corresponding vacuum-oven value. The results are shown in Table 6, along with the standard deviations and the difference between the oven and CI meter values. The validation results have an R2 value of 0.96 and an SEP of 0.76, indicating that the CI meter using Equation (7) can be used to predict the MC of blueberries with sufficient accuracies, useful for the industry. Either the Unscrambler or the SAS method of regression analysis could be used for developing the calibration model with similar performance. Shown in Figure 3 are the CI meter predicted values of the validation group plotted against their vacuum-oven values for all the 40 samples.
Acknowledgements
The authors are grateful to the Oceana Foods, Shelby, MI for supplying the dried cherries and blueberries and their collaboration in this work.
Cite this paper
Chari V.Kandala,RonHolser,JayaSundaram,NaveenPuppala, (2015) Nondestructive Determination of Moisture Content in Dry Fruits by Impedance and Phase Angle Measurements. Journal of Sensor Technology,05,73-80. doi: 10.4236/jst.2015.54008
References
- 1. Brothwell, D. and Brothwell, P. (1998) Food in Antiquity: A Survey of the Diet of Early People. John Hopkins University Press, Baltimore and London, 144-147.
- 2. Hui, YH. (2006) Handbook of Fruits and Fruit Processing. Blackwell Publishing, Oxford, 81.
http://dx.doi.org/10.1002/9780470277737 - 3. AOAC (1990) Official Method of Analysis of the Association of Official Analytical Chemists. No. 934.06, AOAC, Arlington.
- 4. Windham, W.R. (1989) Comparison between Liquid and Paste Karl Fischer Extraction for NIRS Water Calibrations. Journal of the Association of Official Analytical Chemists, 72, 255-258.
- 5. Kandala, C.V.K. and Nelson, S.O. (1990) Measurement of Moisture Content in Single Kernels of Peanuts: A Nondestructive Electrical Method. Transactions of the ASAE, 33, 567-572.
http://dx.doi.org/10.13031/2013.31367 - 6. Kandala, C.V.K., Avula, R., Settaluri, V., Reddy, R.S. and Puppala, N. (2013) Sensing the Moisture Content of Dry Cherries—A Rapid and Nondestructive Method. Food and Nutrition Sciences, 4, 38-42.
http://dx.doi.org/10.4236/fns.2013.49A2006. - 7. Kandala, C.V.K. and Sundaram, J. (2010) Nondestructive Measurement of Moisture Content Using a Parallel-Plate Capacitance Sensor for Grain and Nuts. IEEE Sensors Journal, 10, 1282-1287.
http://dx.doi.org/10.1109/JSEN.2010.2041446 - 8. Kandala, C.V.K., Butts, C.L. and Lamb, M.C. (2008) Moisture Content Determination for In-Shell Peanuts With a Low-Cost Impedance Analyzer and Capacitance Sensor. Transactions of the ASAE, 51, 1377-1381. http://dx.doi.org/10.13031/2013.25221
- 9. Unscrambler, Version 9.7. CAMO Software Inc., Woodbridge.
- 10. SAS Institute (2000) Statistical Analysis Software for Windows, Version 8.1, SAS Institute, Cary.
NOTES
1Mention of company or trade names is for the purpose of description only, and does not imply endorsement by the US Department of Agriculture.
2Moisture contents are expressed on wet weight basis throughout this paper.
3SEC = 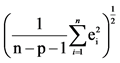 where n is the number of observations, p is the number of variables in the regression equation with which the calibration is performed, and ei is the difference between the observed and reference value for the ith observation.
where n is the number of observations, p is the number of variables in the regression equation with which the calibration is performed, and ei is the difference between the observed and reference value for the ith observation.
4SEP = 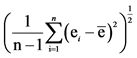 where n is the number of observations, ei is the difference in the moisture content predicted and that determined by the reference method for the ith sample, and
where n is the number of observations, ei is the difference in the moisture content predicted and that determined by the reference method for the ith sample, and 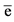 is the mean of ei for all of the samples.
is the mean of ei for all of the samples.





