Journal of Sensor Technology
Vol.1 No.2(2011), Article ID:5569,5 pages DOI:10.4236/jst.2011.12003
Mathematical Modeling of the Amperometric Response to Glucose of Glucose Oxidase Films Deposited by AC-Electrophoresis
Department of Metallurgy and Materials Engineering, MTM, Leuven, Belgium
E-mail: m78ammam@yahoo.fr
Received February 11, 2011; revised March 20, 2011; accepted March 29, 2011
Keywords: Alternating current electrophoretic deposition, glucose oxidase, modeling
Abstract
Previous work illustrated that glucose oxidase (GOx) could be deposited on conducting substrates using asymmetrical alternating current electrophoretic deposition (AC-EPD) to form thick enzyme layers suitable for the manufacturing of highly active biosensors. Here, we modeled the amperometric response of GOx layers to glucose as a function of the thickness of the enzyme layer. The model is based on reaction-diffusion equations with irreversible first-order catalytic reactions. The numerical results displayed qualitative and reasonable quantitative agreement with the experimental data obtained for oxidation currents due to glucose, which increase with the enzyme layer thickness.
1. Introduction
Immobilization of enzymes is used in biosensors to detect the concentration of a specific analyte as a result of the biological recognition between the analyte and the immobilized enzyme [1-6]. Thick enzyme layers have been fabricated via cross linking with glutaraldehyde [7-9], entrapment in polymers or gels and carbon paste mixing [10-12] and, by electrochemical deposition [13, 14]. The purpose of these approaches is to immobilize enzymes in their active state. Recently, we reported that enzymes such as glucose oxidase, glutamate oxidase and b-galactosidase can be deposited using AC-EPD to yield thick, active enzyme layers which were used for the development of highly sensitive biosensors [15-18]. In this regard, it is worth noting that among the advantages of the AC-EPD technique over the existing deposition methodologies we quote the ease of the manufacturing process as well as the high reproducibility due to the automated deposition procedure.
Mathematical models and solutions of enzyme electrodes prepared by various processes such as immobilization in dispersed carbon nanotubes, electropolymerization and encapsulation in membranes have been reported [19-22]. In this note, the steady state amperometric currents of glucose oxidase layers deposited by AC-EPD is modeled as a function of the layer thickness and compared to experimental values.
2. Theoretical Model
A schematic representation of the enzyme modified electrode on which a uniform GOx layer is deposited is illustrated in Figure 1.
The amperometric response to glucose is due to the enzymatic conversion of glucose to hydrogen peroxide and D-glucono-1,5-lactone:

This reaction model shows that for every molecule of glucose that reacts, one molecule of hydrogen peroxide is formed.
As the transport of glucose inside the enzyme film occurs by diffusion, we assume that the concentration c1 of glucose inside the film is governed by the one-dimensional reaction-diffusion equation:
 (1)
(1)
where 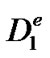 is the effective diffusion coefficient of glucose ([m2·s−1]), k is the forward reaction rate constant
is the effective diffusion coefficient of glucose ([m2·s−1]), k is the forward reaction rate constant
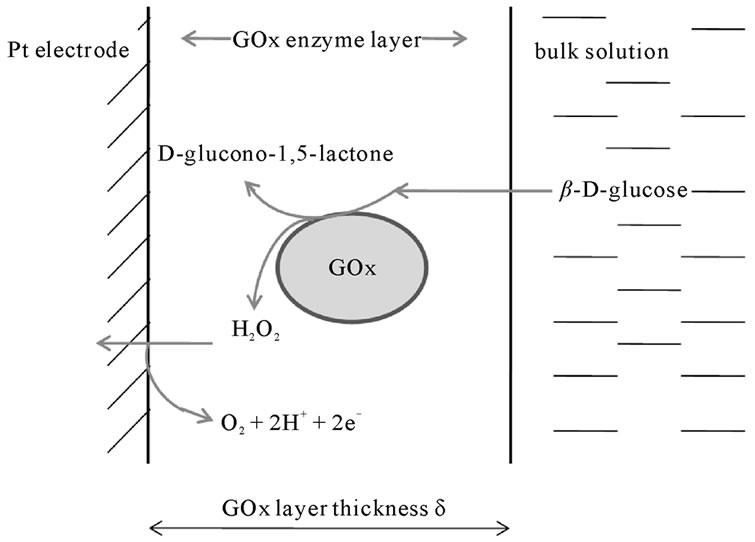
Figure 1. Schematic representation of the electrocatalytic oxidation of glucose inside the GOx enzyme layer deposited by AC-EPD on a platinum electrode.
([s−1]) of the reaction between glucose and oxygen, x is the normal distance to the electrode and δ is the thickness of the enzyme film ([m]). In equation (1), we assume that the reaction rate of glucose is first order in the glucose concentration (kc1). Based on the experimental evidence of Figure 5 of reference [23], this is a valid assumption for the glucose concentrations used in this work. Equation (1) also assumes that the reaction is irreversible or that the backward reaction proceeds at a much smaller rate and that the oxygen concentration is high enough as experimentally observed for the enzyme electrode [16]. Equation (1) is subject to the following boundary conditions:
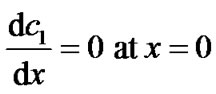 (2)
(2)
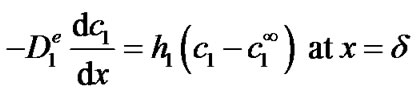 (3)
(3)
where 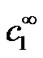 is the glucose concentration in the bulk (in this work 5 mol·m–3). The first boundary condition states that glucose itself is not electrochemically active and hence does not oxidize or reduce on the surface of the electrode (x = 0). This is indeed the case at the applied potential of +0.6 V vs. AgCl/Ag. The second boundary condition states that, at the enzyme film-electrolyte interface, the mass transport by diffusion in the film equals the convective transport in the electrolyte, with h1 the convection coefficient of glucose (m·s−1).
is the glucose concentration in the bulk (in this work 5 mol·m–3). The first boundary condition states that glucose itself is not electrochemically active and hence does not oxidize or reduce on the surface of the electrode (x = 0). This is indeed the case at the applied potential of +0.6 V vs. AgCl/Ag. The second boundary condition states that, at the enzyme film-electrolyte interface, the mass transport by diffusion in the film equals the convective transport in the electrolyte, with h1 the convection coefficient of glucose (m·s−1).
The enzymatically generated hydrogen peroxide is subsequently electrochemically oxidized on the surface of the platinum electrode:
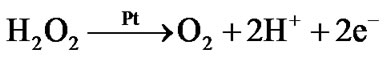
Hence, the concentration c2 of H2O2 inside the enzyme film is governed by the following one-dimensional reaction-diffusion equation:
 (4)
(4)
with 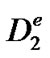 the effective diffusion coefficient of H2O2. This equation is subject to the following boundary conditions:
the effective diffusion coefficient of H2O2. This equation is subject to the following boundary conditions:
 (5)
(5)
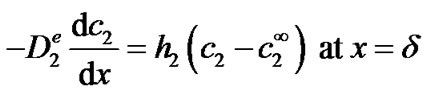 (6)
(6)
where 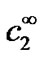 is the concentration of H2O2 in the bulk (in this work 0 mol·m−3). The first boundary condition states that at the applied potential (+0.6 V vs. Ag/AgCl), hydrogen peroxide is mass transport limited inside the enzyme film and its concentration becomes zero on the surface of the electrode. The second boundary condition is identical to equation (3). Equations (1) through (6) can be solved analytically for c2 (see Appendix). The current density i2 (Am−2) due to the oxidation of hydrogen peroxide is proportional to the concentration gradient of hydrogen peroxide on the surface of the electrode according to:
is the concentration of H2O2 in the bulk (in this work 0 mol·m−3). The first boundary condition states that at the applied potential (+0.6 V vs. Ag/AgCl), hydrogen peroxide is mass transport limited inside the enzyme film and its concentration becomes zero on the surface of the electrode. The second boundary condition is identical to equation (3). Equations (1) through (6) can be solved analytically for c2 (see Appendix). The current density i2 (Am−2) due to the oxidation of hydrogen peroxide is proportional to the concentration gradient of hydrogen peroxide on the surface of the electrode according to:
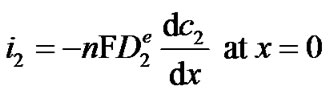 (7)
(7)
where n is the number of the electrons exchanged in the oxidation of one molecule of H2O2 (2 in this case) and F is Faraday’s constant. This results in the following closed-form expression for the current density:
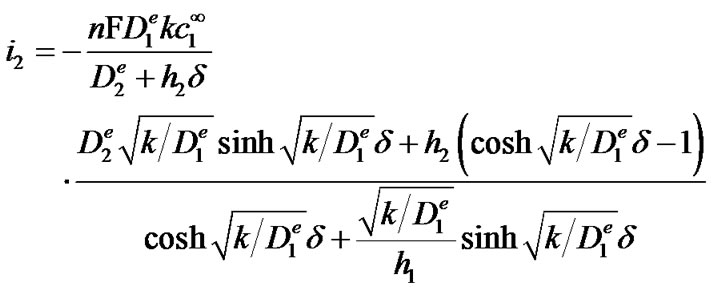 (8)
(8)
3. Results and Discussion
The amperometric response of the GOx film was calculated using equation (8) based on values for the diffusion coefficients found in literature and listed in Table 1. In accordance with reference [24] on the diffusion of organic solutes in biofilms (which we believe to be similar to the enzyme films of this work), we assumed that the ratio of the effective diffusion coefficient inside the enzyme film to the diffusion coefficient in water equals 0.25. The convection coefficients for glucose and hydrogen peroxide were estimated assuming:
 (9)
(9)

Table 1. Diffusion coefficients in water at 25˚C.
where t represents the diffusion layer thickness in the unstirred glucose solution, which is assumed to be 100 μm.
The amperometric response of the GOx film on a Pt disk electrode with a diameter of 1 mm (surface area ≈ 0.78 mm2) to a glucose concentration of 5 mM is plotted in Figure 2 as a function of the thickness of the enzyme layer for various values of the reaction rate constant k. As can be seen, the current due to glucose strongly increases as the thickness of the enzyme layer increases, in accordance with our experiments [15-16]. Figure 2 also displays that when the film reaches a certain thickness (value depending on the rate constant), the current levels off and reaches a maximum. This behavior can be understood as follows: when the film is very thin, almost no glucose is converted to hydrogen peroxide and the current is small. As the film thickness increases, more and more glucose reacts to hydrogen peroxide and the current increases. At a certain thickness, all of the glucose that enters the film is converted to hydrogen peroxide and the current reaches a maximum. When the film becomes thicker, the current drops as part of the hydrogen peroxide that is formed in the film diffuses out before it reacts at the electrode. In our previous experimental study, it was found that the thickness of the enzyme layers after 10, 20 and 30 minutes deposition time are respectively 3, 7 and 11 µm and the corresponding amperometric responses to 5 mM glucose are 665, 1254 and 1804 nA [15], shown as triangles in Figure 2. Figure 2 reveals that the absolute values of the simulated currents are in reasonable agreement with the experimental values assuming a value of order 1 for the enzymatic conversion rate k. When the enzymatic reaction rate k takes on a value of 1 s−1, the model deviates from the experimental values by −10, +13 and +33% for films of resp. 3, 7 mm and 11 mm thickness.
4. Conclusions
The amperometric current response of glucose oxidase layers deposited by AC-EPD to glucose was modeled as a function of the thickness of the enzyme layer. The model is based on reaction-diffusion equations with irreversible first-order reactions. The numerical results are qualitatively and quantitatively in reasonable agreement with the experimental data.
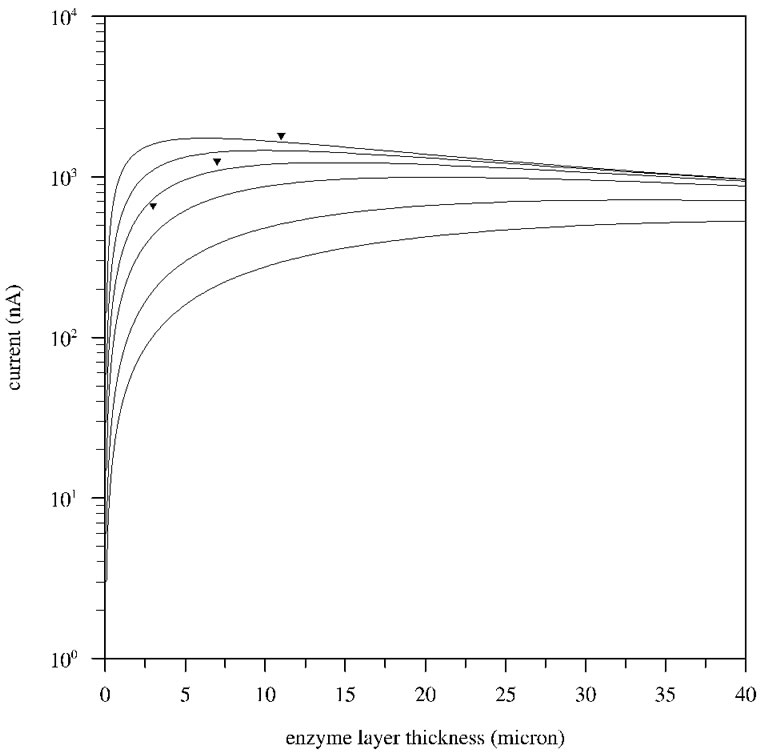
Figure 2. Simulated currents due to 5 mM glucose on a Pt disk electrode with a diameter of 1 mm (≈ 0.78 mm2 surface area) as a function of the enzyme thickness for various values of the reaction rate constant k. From bottom to top, the rate constant k equals 0.1, 0.2, 0.5, 1, 2 and 5 s−1. The experimental data points are shown as triangles.
5. Acknowledgements
The authors acknowledge the support of the Research Fund KU Leuven (GOA/08/007) and the Belgian Federal Science Policy Office (BELSPO) through the IUAP project INANOMAT (contract P6/17).
6. References
[1] A. P. Turner, “Biosensors-Sense and Sensitivity,” Science, Vol. 290, No. 5495, November 2000, pp. 1315-1317. doi:10.1126/science.290.5495.1315
[2] G. Davis, “Electrochemical Techniques for the Development of Amperometric Biosensors,” Biosensors, Vol. 1, No. 2, 1985, pp. 161-178.
[3] U. J. Krull, R. S. Brown, E. T. Vandenberg and B. D. Hougham, “Engineering in Medicine and Biology Society,” The International Conference on Rehabilitation Robotics, Zurich, 29 June-1 July 2011, pp. 793-794.
[4] D. R. Thévenot, K. Toth and G. S. Wilson, “Electrochemical Biosensors: Recommended Definitions and Classification,” Pure and Applied Chemistry, Vol. 71, No. 12, July 1999, pp. 2333-2348.
[5] W. Schuhmann, “Non-Leaking Amperometric Biosensors Based on High-Molecular Ferrocene Derivatives,” Biosensors & Bioelectronics, Vol. 8, No. 3-4, 1993, pp. 191- 196. doi:10.1016/0956-5663(93)85032-J
[6] G. S. Wilson and M. Ammam, “In Vivo Biosensors,” FEBS Journal, Vol. 274, No. 21, November 2007, pp. 5452-5461. doi:10.1111/j.1742-4658.2007.06077.x
[7] F. López-Gallego, L. Betancor, C. Mateo, A. Hidalgo, N. Alonso-Morales, G. Dellamora-Ortiz, J. M. Guisán and R. Fernández-Lafuente, “Enzyme Stabilization by Glutaraldehyde Crosslinking of Adsorbed Proteins on Aminated Supports,” Journal of Biotechnology, Vol. 119, No. 1, September 2005, pp. 70-75.
[8] J. F. Kennedy, B. Kalogerakis, J. M. S. Cabral, “Surface Immobilization and Entrapping of Enzymes on Glutaraldehyde Crosslinked Gelatin Particles,” Enzyme and Microbial Technology, Vol. 6, No. 3, March 1984, pp. 127- 131. doi:10.1016/0141-0229(84)90119-4
[9] R. J. Geise, J. M. Adame, N. J. Barone and A. M. Yacynych, “Electropolymerized Films to Prevent Interferences and Electrode Fouling in Biosensors,” Biosensors and Bioelectronics, Vol. 6, No. 2, 1991, pp. 151-160. doi:10.1016/0956-5663(91)87039-E
[10] M. Campás and J.-L. Marty, “Methods in Biotechnology: Encapsulation of Enzymes Using Polymers and Sol-Gel Techniques,” 2nd Edition, Vol. 22, Humana Press, Totowa, 2008.
[11] X. Chen, Y. Hu and G. S. Wilson, “Glucose Microbiosensor Based on Alumina Sol–Gel Matrix/Electropolymerized Composite Membrane,” Biosensors and Bioelectronics, Vol. 17, No. 11-12, December 2002, pp. 1005- 1013. doi:10.1016/S0956-5663(02)00093-3
[12] M. Kumakura, “Effect of Heat Treatment on Enzymes Entrapped into Polymer Gels,” Journal of Molecular Catalysis B: Enzymatic, Vol. 1, No. 1, December 1995, pp. L1-L6. doi:10.1016/1381-1177(95)00007-0
[13] X. Chen, N. Matsumoto, H. Hu and G. S. Wilson, “Electrochemically Mediated Electrodeposition/Electropolymerization to Yield a Glucose Microbiosensor with Improved Characteristics,” Analytical Chemistry, Vol. 74, No. 2, 2002, pp. 368-372. doi:10.1021/ac015628m
[14] M. Ammam and J. Fransaer, “Micro-Biofuel Cell Powered by Glucose/O2 Based on Electro-Deposition of Enzyme, Conducting Polymer and Redox Mediators: Preparation, Characterization and Performance in Human Serum,” Biosensors and Bioelectronics, Vol. 25, No. 6, February 2010, pp. 1474-1480. doi:10.1016/j.bios.2009.11.001
[15] M. Ammam and J. Fransaer, “AC-Electrophoretic Deposition of Glucose Oxidase,” Biosensors and Bioelectronics, Vol. 25, No. 1, September 2009, pp. 191-197.
[16] M. Ammam and J. Fransaer, “Glucose Microbiosensor Based on Glucose Oxidase Immobilized by AC-EPD: Characteristics and Performance in Human Serum and in Blood of Critically Ill Rabbits,” Sensors and Actuators B: Chemical, Vol. 145, No. 1, March 2010, pp. 46-53. doi:10.1016/j.snb.2009.11.015
[17] M. Ammam and J. Fransaer, “Highly Sensitive and Selective Glutamate Microbiosensor Based on Cast Polyurethane/AC-Electrophoresis Deposited Multiwalled Carbon Nanotubes and then Glutamate Oxidase/Electrosynthesized Polypyrrole/Pt Electrode,” Biosensors and Bioelectronics, Vol. 25, No. 7, March 2009, pp. 1597- 1602.
[18] M. Ammam and J. Fransaer, “Two-Enzyme Lactose Biosensor Based on b-Galactosidase and Glucose Oxidase Deposited by AC-Electrophoresis: Characteristics and Performance for Lactose Determination in Milk,” Sensors and Actuators B: Chemical, Vol. 148, No. 2, July 2010, pp. 583-589. doi:10.1016/j.snb.2010.05.027
[19] M. E. G. Lyons, “Transport and Kinetics at Carbon Nanotube-Redox Enzyme Composite Modified Electrodes Biosensors,” International Journal of Electrochemical Science, Vol. 4, No. 1, 2009, pp. 77-103.
[20] P. N. Bartlett and R. G. Whitaker, “Electrochemical Immobilization of Enzymes: Part I. Theory,” Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, Vol. 224, No. 1-2, June 1987, pp. 27-35. doi:10.1016/0022-0728(87)85081-7
[21] P. N. Bartlett and K. F. E. Pratt, “Modeling of Process in Enzyme Electrodes,” Biosensors and Bioelectronics, Vol. 8, No. 9-10, 1993, pp. 451-462. doi:10.1016/0956-5663(93)80030-S
[22] J. J. Kulys, V. V. Sorochinskii and R. A. Vidziunaite, “Transient Response of Bienzyme Electrodes,” Biosensors, Vol. 2, No. 3, 1986, pp. 135-146. doi:10.1016/0265-928X(86)80001-3
[23] K. Karmali, A. Karmali, A. Teixeira and M. J. Marcelo Curto, “Assay for Glucose Oxidase from Aspergillus Niger and Penicillium Amagasakiense by Fourier Transform Infrared Spectroscopy,” Analytical Biochemistry, Vol. 333, No. 2, October 2004, pp. 320-327. doi:10.1016/j.ab.2004.06.025
[24] P. S. Stewart, “Diffusion in Biofilms,” Journal of Bacteriology, Vol. 185, No. 5, March 2003, pp. 1485-1491. doi:10.1128/JB.185.5.1485-1491.2003
[25] L. G. Longsworth, “Diffusion in Liquids and the Stokes- -Einstein Relation,” In: T. Shedlovsky, Ed., Electrochemistry in Biology and Medicine, John Wiley & Sons, New York, 1955, pp. 225-247.
[26] R. J. Meyer, “System-Nr. 3. Sauerstoff-Lieferung 7. Wasserstoffperoxid. 1966 IV, XXVII, 430 Seiten, 82 Figuren. Ganzleinen DM 398,-,” Berichte der Bunsengesellschaft für physikalische Chemie, Vol. 71, No. 5, 1967, p.537.
Appendix: Derivation of Equation (8)
Equation (1) is a second order differential equation with constant coefficients for which the general solution is given by:
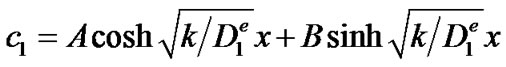
with A and B two integration constants, whose value can be determined from the boundary conditions (2) and (3). Equation (2) yields B = 0 while equation (3) yields:
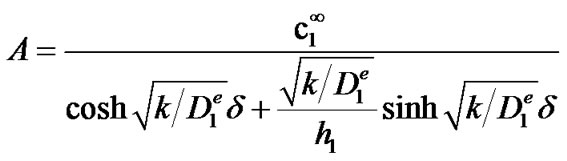
yielding the following solution for c1:
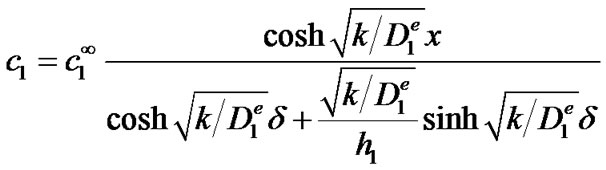
With the solution of c1, the general solution of Equation (4) can be found:
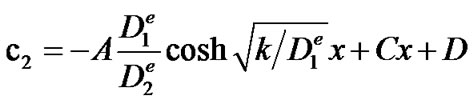
The two integration constants C and D which can be found from the boundary conditions (5) and (6), result in the following solution for c2:

from which equation (8) can be derived by differentiation according to equation (7).

