Advances in Molecular Imaging
Vol.07 No.02(2017), Article ID:78168,35 pages
10.4236/ami.2017.72002
An Alternative Model to Radon Transform for Gamma Ray Emission Tomography
Christian Jeanguillaume1, Richard Simonnet2, Christine Cavaro-Menard1, Abdelha Douiri3, Ines Bouali1, Jean Jacques Loeb4
1LARIS Laboratoire Angevin de Recherche en Ingenierie des Systemes, Universite d’Angers, Angers, France
2Direction Generale de l’Armement Techniques Terrestres, Bourges, France
3King College London, London, United Kingdom
4LAREMA Laboratoire Angevin de Recherche en Mathematiques, Universite d’Angers, Angers, France

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC 4.0).
http://creativecommons.org/licenses/by-nc/4.0/



Received: April 1, 2017; Accepted: April 27, 2017; Published: April 30, 2017
ABSTRACT
The Radon transform fits badly Single Photon Emission Tomography (SPECT). However, Thin Holes Collimator (THC) and Radon model are widely used. The CACAO project has been proposed to enhance the quality of SPECT images. CACAO is a short hand notation for computer aided collimation tomography. The main idea of this project is to use collimators with much larger holes to increase the sensitivity, and slightly longer holes to increase the spatial resolution. The acquisition sequence includes a translation. The Radon projection is replaced by a 2D sum. A dedicated reconstruction algorithm has been developed. If the physical advantage of the project in terms of sensitivity and spatial resolution is generally admitted, a question remains unanswered: Would the ill-posedness of the inverse problem ruin the quality of the reconstructed images? In this article, a representation of the 2D direct problem matrix is derived. This allows us to compare the two inverse problems (CACAO versus THC). The condition number was used for this comparison. We studied the variation of these condition numbers with several parameters. For a proper set of parameters, the CACAO inverse problem may appear easier to solve and more accurately than the THC one.
Keywords:
Radon Transform, Tomography, SPECT, Large and Long Hole Collimators, Inverse Problems

1. Introduction
Since its invention by H. A. Anger [1] , the gamma camera has been used extensively in medical practice, mostly with a thin-parallel-hole-collimator (THC). It should be noted that, in gamma ray imaging, tomography has taken some time to be widely used in clinical practice. In contrast in X ray imaging, computer tomography (CT) was a breakthrough, due to the sudden and huge improvement in image quality that it brought. The mathematical model currently used in THC-SPECT is based on the Radon transform [2] . However, if this model is well suited to Xray imaging (CT), we think, it is not well adapted for THC-SPECT. In effect, to perfectly fit the Radon transform the collimator would need to have infinitely long and infinitely narrow holes. Such an “ideal” collimator would not allow any photons to reach the detector, and therefore no image could be reconstructed. Needless to say these are the photons which carry the information from the patient to the detector. In practice engineers have made a trade off. They have tried to deviate slightly from this “ideal” collimator but not too excessively. The results is a poor sensitivity: 10,000 photons lost for each 1 which reaches the detector and a poor spatial resolution of 8 to 10 mm (compared to the detector intrinsic resolution ≈ 3 mm). Furthermore, this poor spatial resolution worsens with the source to collimator distance (15 mm in the center of a patient). This compromise is the bottleneck of the conventional THC-SPECT. To visualize the problem Figure 1 shows the motion followed by a gamma camera in a standard THC-SPECT acquisition. Figure 2 shows an example of an acquisition made with this system for an object composed of 2 point sources.
Several authors have tried to increase the sensitivity of the gamma camera. Two-headed cameras or multi-pinholes [3] can increase this sensitivity with the number of heads or pinholes. Zhang et al. [4] , in their interesting study posited the hypothesis that high resolution (very-thin-hole) collimators may not be optimal for SPECT. Furthermore, they demonstrated that the tomographic
Figure 1. Scheme of a THC-SPECT acquisition motion in a 2D reduction plane. The object is composed of only 2 point sources (one in blue, one in red). The gamma camera makes a complete rotation around the object. The 2 point sources (blue and red) are common to the first 4 figures.
Figure 2. Representation of a conventional THC-SPECT acquisition data of an object composed of 2 point sources one in blue, one in red. The signal emitted by each source has been colored accordingly in blue and red to fit the colors of the point sources of Figure 1. These colors are purely fictitious, for the sake of pedagogy. In the real life 2 sources of the same isotope emit photons of the same energy. Horizontal abcissa linked to the detector, vertical axis angle of acquisition f.
reconstruction could help in restoring part of the “lost” resolution due to the use of slightly larger holed collimators. Lodge [5] proposed a further increase in sensitivity through the use of very large holes in one dimension but still thin in the other. To acquire sufficient information, a double rotation motion is applied to the collimator-detector head during the acquisition. The reconstruction program needs to use 2 inversions of the radon transform.
We stopped the introduction here temporarily to depict the plan of the article. A complete understanding of the problem cannot be attained without some knowledge of the alternative model. This is described in Chapter 2. This section presents the definition of the project (2.1) followed by the mathematical analytical model (2.2) and then the physical advantages of the project are briefly described (2.3). After this description, the problem discussed in this article can be described in Chapter 3. This chapter completes this long but necessary intro- duction. The method used for the comparison of the classical THC-Radon inverse problem versus the alternative CACAO project is detailed in Chapter 4. The results are described in Chapter 5. The results are followed by a discussion 6 and a conclusion 7. The methods, Chapter 4 are divided as follow: Subchapter (4.1) gives a reminder of the condition number definition. Then we derive the impulse response function of the CACAO project (4.2) in a total and a partially attenuating collimator model (4.3). Section (4.4) explains the calculation of the transfert matrix. The THC model used is described in Section (4.5). The results begin with a study of the condition number in relation to the geometry of the collimator (5.1). This study is first presented with very small matrix dimensions in order to get a better grasp of the intervening parameters (5.2, 5.3). The following 2 chapters of the results (5.4 to 5.6) show a comparison of the condition number for the two problems. This comparison is studied with more realistic matrix sizes (up to 64 × 64). Finally noiseless and noisy image simulations are depicted (5.7, 5.8).
2. Purpose, the CACAO Project
To improve the quality of SPECT images, and avoid the drawbacks of the Radon modelling, we proposed the CACAO project. Subchapters 2.1 to 2.3 give the necessary background to understand the problem described in Subchapters 2.1.
2.1. Definition
The CACAO project [6] was proposed to avoid the bottleneck caused by conventional thin-hole-collimators. For the sake of simplicity, the CACAO project is presented here in a 2D reduction. This project shares with THC-SPECT a gamma ray detector position and energy sensitive. It differs by having a collimator with larger and longer holes, an added linear motion in the acquisition sequence, and a mathematical model which takes full account of the geometry of the collimator. It must be understood that larger holes means dramatically larger holes. Figure 3 may help to provide an understanding of the CACAO project. The hole has been chosen as large as 2/3rds the length of the object.
The exact response of the system will be calculated in the following section with the help of Figure 5. An initial examination of this Figure, may allow a better understanding of the subject.
During the linear scan the set collimator + detector travels from the left to the right of Figure 5. This Figure is divided vertically into 3 rows and horizontally into 5 columns. The 5 sectors or columns (from 1 to 5) are limited by 4 special positions of the set that have been labeled with the letters a, b, c, d. The bottom part of the figure shows a point source (S) and the set collimator + detector in the 4 special position limits (detector is shaded blue, collimator is pinstriped). The upper part of the figure is a drawing representing the acquired data after the linear scan. And the text between the upper and the lower parts represents the algebra which will be explained later. Let us start with the left part of the figure,
Figure 3. Scheme of a CACAO acquisition sequence in a 2D reduction plane, the object is composed of only 2 point sources (one in blue, one in red). The gamma camera with a very-large-hole collimator begins the acquisition with a linear motion from left to right, then the camera turns counterclockwise by 90 and goes from bottom to top. for a second linear scan. In this example the acquisition is finally composed of 4 linear scans.
when the detector is further left than position a, no photons (emitted by S) can reach the detector. At the right of position a and before position b the left part of the detector is illuminated. It is important to remember that the hole is a lot larger than the detector’s spatial resolution. In this example we have chosen a collimator hole with a width of 21 pixels. So if we represent the position of the set detector + collimator in the horizontal axis and the signal recorded by the 21 pixels in the vertical axis, (left part up, right part down) the progressive illumination of the detector during the scan can be represented by a triangle (zone 2). Between positions b and c the detector is completely illuminated. The drawing of the set detector + collimator at position c has been represented behind position b and in a lighter shade of gray. In this area 3 the illumination can be represented by a rectangle. Using symetry we have a triangle in area 4. And nothing in area 5. Finally the data resembles a parallelogram. Due to geometrical considerations the greater the distance between the source and the collimator, the larger and the more slanted the parallelogram. Figure 4 shows a 2D example of the 2 point sources CACAO acquisition from Figure 3. The response of each point source has been colored accordingly in blue and red. One can observe that when the source is near the entrance to the collimator the parallelogram is in an upright position. The center of the parallelogram evolves along sinusoids similar to Figure 2 but limited to only 4 different angles.
2.2. Analytical Description
The analytical description of the CACAO transform is described here in a 2D reduction. With the Radon transform the integration is made on a line (the projection line). With CACAO the integration is made over a trapezoidal surface.
Figure 4. Representation of CACAO acquisition data of an object composed of 2 point sources. The signal of each source has been colored accordingly in blue and red to fit Figure 3. Horizontal abcissa: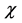 , vertical axis: product
, vertical axis: product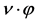 . For reasons which will become clear in the next chapter, each point source gives a signal shaped like parallelograms. The 4 subfigures, correspond to the 4 linear scans previously described in Figure 3.
. For reasons which will become clear in the next chapter, each point source gives a signal shaped like parallelograms. The 4 subfigures, correspond to the 4 linear scans previously described in Figure 3.
Figure 5. Schema representing the CACAO response function to one source in a linear scan.
Figure 6 depicts the variables used.
Figure 6. Scheme of the notations used to describe the 2D direct problem.
A transverse section of the patient is represented by the density of radio-active sources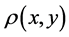 . The collimator has been simplified to a unique hole (width D, depth P). This hole can rotate around the patient and can also perform a linear motion along the u axis. The coordinate system x, y is considered at rest while the rotating coordinates u, w follow the rotation of the collimator-detector, measured by
. The collimator has been simplified to a unique hole (width D, depth P). This hole can rotate around the patient and can also perform a linear motion along the u axis. The coordinate system x, y is considered at rest while the rotating coordinates u, w follow the rotation of the collimator-detector, measured by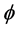 .
.
Photons entering the detector are localized by their position in the hole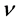 , the position of the hole in the u coordinate measured by
, the position of the hole in the u coordinate measured by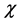 , and the angle of rotation
, and the angle of rotation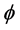 . Therefore, the description of the direct problem aims to define the acquisition function
. Therefore, the description of the direct problem aims to define the acquisition function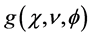 , knowing the distribution of the radioactive sources
, knowing the distribution of the radioactive sources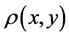 . Elementary geometry considering only photons traveling in the air (no attenuation in the patient), leads to an integral equation for the direct problem. This equation gives
. Elementary geometry considering only photons traveling in the air (no attenuation in the patient), leads to an integral equation for the direct problem. This equation gives 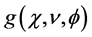 in terms of
in terms of 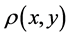 or equivalently
or equivalently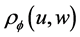 . It is obtained by considering the surface integration in a polygon bounded by the 2 extreme rays touching the 2 corners of the collimator entrance hole. This polygon is also limited by the largest camera orbit (
. It is obtained by considering the surface integration in a polygon bounded by the 2 extreme rays touching the 2 corners of the collimator entrance hole. This polygon is also limited by the largest camera orbit (


where
- 




- 

- 
- 
- 
- 

- 
2.3. A Brief Reminder of the Physical Advantages of the CACAO Project
These potential advantages have already been published [6] [7] , and are com- mented here for the sake of clarity.
2.3.1. Sensitivity
The sensitivity of a thin parallel hole collimator can be estimated by the following formula (valid in 3D). The sensitivy 

where D is the diameter of the collimator hole, P is the length of the collimator hole, K is a coefficient depending on the shape of the holes (rectangular, hexagonal…) and t is the thickness of the septa. This formula is valid for conventional thin-hole-collimators (THC), and it would stand for the CACAO project for a multiholes collimator. Compared to THC, the CACAO sensitivity
could be superior, by a factor of 100 or more by increasing 

some order of magnitude, conventional THCs work with geometrical sensitivities
of 


system by 625 times in 3D. For the sake of simplicity, the description in this paper involves only one hole. But a real implementation of the system will have many holes arranged in a compact pattern. This multi-hole realization will justify the formula (2), and will reduce the extent of the linear scanning motion required during the acquisition, at the price of a larger detector. It is to be noted that the third term of the formula (2) represents the ratio of free surface of the detector to the hidden surface (commonly covered by lead). It will be discussed later.
2.3.2. Spatial Resolution
In the conventional THC case, increasing the hole diameter deteriorates the spatial resolution. In contrast, in the CACAO project this fact is no longer true. This point may be difficult to understand due to the commonly held belief that:
To better understand why this fact is only true for THC, let us draw a parallel with Computerized Tomography. In this system, the signal emanating from a line of voxels is recorded in an acquisition element. The volume corresponding to this line of voxels is thin but quite long (generally 20 cm at the level of the patient’s head and 70 cm at the belly). However a huge number of acquisitions combined with the reconstruction process allow to achieve a milimetre resolution in this long volume.
The following figure examines the physical and geometrical factor governing the spatial resolution of both systems.
The left part of Figure 7 represents a THC collimator with a detector of intrinsic spatial resolution




This formula is based on a gaussian model, where the FWHM: Full width at Half Maximum of the convolution of 2 gaussians, is given by a mean square of the corresponding FWHM’s.
The right part of Figure 7 represents a CACAO collimator with the same detector intrinsic spatial resolution 

Figure 7. Scheme showing how the physical dimensions of the collimators influence the spatial resolution in THC (left) and in CACAO (right). The dimensions have been exaggerated for the sake of pedagogy. The upper part of the figure describes the geometry of both collimators, each one is associated with a detector pixel, and the extreme rays emanating from this detector pixel. The lower part of the figure shows the signal recorded by these detector pixels (THC left, CACAO right) when a point source is scanned along the bottom line of the upper subfigure. See text for a detailed description.

where P is the depth of the collimator hole (CACAO) and 



2.3.3. Quality of Collimation
Another advantage of the CACAO project is the possibility to use larger septa (the walls between the holes of the collimator). The width of the septa has already appeared in the formula (2). Currently THCs use very thin septa (t = 0.015 mm for example) which let 5% of the photons to go through the septa and be detected. Due to the huge number of holes (40,000), a tiny increase of the thickness of the septa will dramatically reduce the sensitivity of conventional systems. On the contrary, for CACAO with only 10 holes or so, in the 600 mm field of view of the camera, a thickness of 2 mm or more will have a very limited effect in the sensitity. By the same token, it can greatly reduces the septal penetration.
2.3.4. Pixelated Detectors
Finally, it has been published that a conjoint use of the CACAO project with pixelated detectors presents a synergistic improvement [8] . These semiconductor detectors can greatly improve the spatial resolution of the currently used detector. For a NaI detector the intrinsic resolution (

3. The Problem
The physical advantages of the CACAO project in term of increased sensitivity are clear and have possibly been accepted by many readers. With larger holes, one can collect more photons. It is also clear that the information is carried by these photons. However two arguments can be raised against this project.
The first is the following: Do the photons collected with CACAO carry the same information quality as the photons collected with THC SPECT in terms of location?
The second question is: Would the gain obtained by the increased number of collected photons be hampered by the difficulty of solving the inverse problem? In other words: which factor will be the greatest: 1) the noise amplification inherent in the mathematical calculation of the reconstructed image or 2) the improvement of the signal to noise ratio of the acquisition brought about by the increased number of photons?
Both these questions are addressed in this article. In fact a positive answer to these questions based on information theory argument has already been published [9] . In this article we studied the multiplex volume (the volume of the object sending photons to a single detector pixel), and we showed that: one can obtain better reconstructed image with a large multiplex volume with precise boundaries (CACAO), than with a small multiplex volume with blurred boundaries (THC).
But we offer here another mathematical argument, based on linear algebra theory. This article studies the difficulty in solving the CACAO problem and compares it to the conventional THC-SPECT problem. To derive this comparison we first calculated the direct matrix of both the CACAO project and the THC-SPECT. The physical considerations for both systems were chosen so as to be equivalent. Then we calculated the condition number of these matrices. The condition number of a matrix measures the accuracy of the solution of the linear equation system and its noise sensitivity. Therefore, with equivalent noise in the data (second member of the equation), a better (lower) condition number of the transfer matrix will give a better solution, e.g. better images.
4. Methods
4.1. Condition Number, Inverse Problem
The condition number [10] , here noted 
Considering the linear system

If 

For practical reasons the tomographic reconstruction is nowadays calculated by computer and the reconstructed image has a finite number of pixels:









In SPECT the main source of noise is due to photon counting (shot noise) and is well modelled by a Poisson distribution. For a large number of collected
photons, 
photons.
Here is an illustration of the meaning of the condition number. Let us take two extreme cases. We will begin by the easiest problem to inverse. For example, a problem whose direct matrix is identity. In this case, whatever the matrix dimension, the condition number will be one. One is the smallest condition number possible. In this simple case, the inverse problem is obviously very easy because no calculations are needed. The data measured is the results, without any further calculations.
To show an example fo a difficult (badly conditioned) problem: Imagine a matrix full of 1 with 



4.2. Impulse Response Function in the Total Attenuation Model (Perfect Collimator)
To shorten the notation, all the distances are expressed as a ratio with the width of the pixel of the image, and of the detector (for the sake of simplicity we consider the image pixel having the same width of the detector pixel). All the dimensions are then given by a pure number without units.
We will develop in this chapter an analytical calculation of the response function 



The response function for other values of 


First, the extreme lateral zones (① and ⑤ on Figure 5). They are defined for:


receive any photon (full attenuation model), so
For the central zone (③ on Figure 5) 
light up and the illumination will follow the Lambert’s cosine law and inverse
square law.: 

depends on the brightness of the source; d is the distance from the source to the detector, and 


The angle 

illumination law:

This law of illumination is also valid for the two remaining domains (② and ④ on Figure 5).
However, in these domains, the detector is not completely lit up. Notice, for example, the 2nd domain (Figure 8) the detector is lit up under the abcissa 

Figure 8. Schema depicting the geometry of the calculation of

The upper part of Figure 5 shows the parallelogram representing the support of the impulse function in the plane 
this parallelogram are: 

edges and 

4.3. Septal Penetration
To extend the previous calculation in a more realistic model, we study the shadow areas (for example above

Figure 9. Septal penetration notations.
By considering the similar triangles made by the w axis and the ray’s path, elementary geometry leads to the length of the path in the attenuating medium: (

where 



Figure 10. Example of the impulse response function with septal penetration calculation (red dashed line) and without (blue continuous line). y axis: intensity recorded, x axis: part of the 

consequence, we did not further extend the model to hold the width of the septa. (see section 5.2). We did not pay attention to rays crossing the edge of the collimator close to the detector. With a single hole collimator this event will be irrelevant because the detector and the collimator can be fitted to the same size.
4.4. Direct Matrix Calculation
This section describes the calculation of the direct matrix, in a discrete-discrete form [11] . As we derived a continuous impulse function in the preceding chapter, we have to make it discrete. The emitting source is considered composed of point sources situated in the center of the pixels. This choice is guided by the possibility of high spatial resolution study. At the detector level, we integrate the response function over the width of the detector pixel (model well adapted to semiconductor detectors). This approach is used for both cases.
A program (written in Python) calculates the impulse function

As a simple example, for a 4 × 4 image matrix only 12 pixels are considered (Figure 11). The matrix of the direct problem, will be composed by 12 columns. The columns are sorted as in Figure 11. Let 








Figure 11. Schema exhibiting for a 4 × 4 reconstruction image, the numbering of the pixels in the disc of interest.
We further calculated the extent 


Figure 12. Schema exhibiting the geometry of the calculation of the field width (
We introduce 





Due to the possible septal penetration, we use a 

Figure 13. Small extract of a CACAO direct problem matrix 
in gray scale, with











4.5. The THC Direct Problem Matrix
Several possibilities have been proposed to derive the THC-SPECT transform in a discrete form. To be comparable with the previous calculation, we needed a model which took into account the septal penetration and the variation of the collimator response with the source to collimator distance. A Gaussian model was chosen to fulfill a compromise between simplicity and accuracy. We used the experiment driven measurements of Youngho Seo et al. [12] . These authors proposed the following parameters for the Gaussian FWHM for a VPC-45 LEHR collimator and for a Tc99m source without scatter or attenuation correction in the sources:

where all the measurements are expressed in centimeters, and where w is the source to collimator distance. As described earlier, the calculation is limited to the points located in a circular area (Figure 11). To match the former description, we evaluate the coordinates of each pixel center in this circular area. The corresponding Gaussian functions are integrated through the boundaries of the detector pixels (fixed to 3 mm). We then obtain a matrix (



An example of matrix 





Figure 14. Small extract of a matrix 
4.6. Simulation and Reconstruction by the Least Square Method
4.6.1. SNR, SNRG, ppp
To illustrate the effect of the condition number, we have simulated some acquisitions of a resolution pattern (64 × 64). The noise free acquisition was calculated for both systems (THC and CACAO) by a simple product with both direct matrices. A gaussian noise was drawn in both acquisitions. Let 



where 

and 



This formulae can be applied either to the acquisition or the reconstructed image. For a reconstructed image obtained from a noise free simulated acquisition the degraded image comes from the roundoff errors, and the ideal image is the initial simulated object.
For noise free acquisition-reconstruction this SNR is expressed in decibels (db) 






For the noisy data, a snrg is calculated by the ratio of the SNR of the reconstructed image (




4.6.2. Resolution Pinstripe Pattern
For the whole simulation we have chosen a resolution pinstripe pattern define as follow: If 


The square image formerly described is then chopped according to 

4.6.3. Acquisition Simulation
The pinstripe pattern is then simply multiplied by both direct matrix to give the noise free acquisitions.

For noisy simulation, a Gaussian noise is added to each non-zero pixel of the acquisition. However to vary the SNR, the data are scaled by a simple multi- plication. The numbers of non zero pixels (


But the SNR’s were nearly the same at acquisition level (depending only on the draw). To illustrate that point, the following Figure 15 and Figure 16 show both acquisitions for a pseudo-Poisson expectancy of 10 photons per pixels.
For each simulated acquisition sample we reconstructed an image by the least square method. This method is easily done by the calculation of a pseudoInverse 

Figure 15. Classical THC acquisition 


Figure 16. CACAO acquisition 





In the last equation, 



5. Results
Three parts can be differentiated in the results: in the first we study the condition number with the parameters of the model, with calculation on small matrix size, subchapters: 5.1 to 5.3.
In the second part we make the condition number comparison: THC versus CACAO, with more realistic matrix sizes (up to 64 × 64), subchapters: 5.4 to 5.6.
The final part is devoted to the simulations and reconstructions of noise free and noisy images. 5.7 to 5.8.
5.1. Variation of the CACAO Condition Number with the Collimator Dimensions
Figure 17 shows an example of the variations of the condition number of the CACAO direct problem with the value of D ranging from 2 to 55 for 2 different P values






In the following chapters, we will study the variations of the condition numbers for both systems (THC and CACAO) with the common parameters of the problem. We will first focus on the parameters that are important to understand the validity of this paper.
Figure 17. CACAO condition number versus D for two P values: 21 (blue curve) and 30 pixels (red curve).
5.2. Variation of the Condition Numbers with the Cut-Off Value
As we have used a Gaussian model for the THC system and an exponential attenuation for the CACAO system, these two functions extend to infinity. These functions were integrated numerically (Python with Scipy and Numpy package). Obviously, very small values (under 
Table 1 shows the condition numbers calculated for the two systems for various cutoff. The condition number levels off in a wide range of cut-offs. For higher values of cut-offs the condition number began to decrease (

Table 1. Variation of the condition number with the cut-off value.
5.3. Variation of the Condition Numbers with the Number of Acquisition Angles
The variations of the condition numbers of the system matrices, versus the number of acquisition angles, exhibit a rather similar behaviour for both systems. As the number of angles increases, the condition number decreases until it reaches a plateau (Figure 18).
Figure 18. Comparison of the condition number with the number of acquisition angles. THC: Blue curve, CACAO: Red curve.
Values for this figure: Pixel width = 3 mm, THC: VPC-45 LEHR, CACAO:








5.4. Variation of the Condition Numbers with the Orbital Radius
The orbital radius Rg determines the source to detector distance. For both acquisitions (THC or CACAO) increasing Rg increases the condition number as shown in Figure 19.
Pixel width = 3 mm, 








Figure 19. Condition number versus orbital radius
5.5. Variation of the Condition Numbers with the Size of the Reconstructed Image
The size of the reconstructed image matrix is obviously a very important factor. The caculations performed so far have been made with a dramatically small image size, for the sake of simplicity. For real applications, however, enormous matrix size becomes compulsory. Figure 20 exhibits the influence of the image size, while ranging from 

image matrix size with the formula:
Figure 20. Condition number versus size of the image. THC: Blue curve, CACAO: Red curve.
Rg follows the formula:
The number of acquisition angles for the THC configuration was chosen high:

Pixel width = 3 mm, 









With a 64 × 64 matrix size the number of columns of the matrix was 3196 (number of pixels in the circular cache).
Table 2 gives the values corresponding to Figure 20.
Table 2. Condition number versus image size.
5.6. Study of the Spectrum of the Singular Value Decomposition
Figure 21 was calculated from the complete spectrum of the singular values for the classical THC approach and the CACAO project. This figure does not represent the singular values themselves but rather the ratio of the greatest
singular value over the ith.
very large we have used a logarithmic scale. The singular values are sorted in descending order. Therefore the greatest is the first (
Figure 21. Log of the ratio of the largest singular value to the ith singular value for the transfer matices of an image 64 × 64

Figure 22 shows the position of the cross point which is where the two curves on Figure 21 meet. Figure 22 shows the cross point position variation depending image size. The position is measured as a percentage of the matrix rank (number of singular values). The curve begins by a small climb, due to the limited number of singular values. For example the point of the curve

Figure 22. Cross point position measured in percentage of SVD for image 4 × 4, 8 × 8, 16 × 16, 32 × 32 and 64 × 64 and others parameters identical to the former figure.
5.7. Reconstruction Results from Noise Free Acquisitions
In the following two sections the parameters of the collimation and of the acqui- sition will remain fixed. These parameters are given in the following Table 3.
Table 3. Parameters chosen for the two systems in the last two chapters.
The same digital pinstripe resolution pattern (64 × 64) (24) is first multiplied by both direct matrices (THC and CACAO), to give the 2 (noise free) acquisitions. The two estimates are calculated by a simple matrix multiplication with both pseudo Inverses (18). Due to the relatively small size of the image and the absence of noise, both results are excellent. These two estimates are not depicted here, because the human eye cannot detect difference from the original image (24). However, the computer can: both SNR in decibels are given in the last row of the previous Table 3.
5.8. Noisy Simulations Results
For the two chosen systems, (whose parameters are given in Table 3) and for 5 choices of signal to noise ratio at the acquisition level, we simulated noisy acquisitions then we reconstructed the corresponding least square estimates. By the same token, for both systems, the acquisition is different and simulated noises are different. To average these necessary differences, 10 simulations of noise were drawn at each noise level. for both systems. Two very noisy acquisitions are depicted in Figure 15 and Figure 16. For each of these 100 simulations (5 × 10 × 2) we calculated the gain in SNR by formula 14. The different values of snrg are depicted in Figure 23.
Figure 23. Signal to noise gain (snrg) for the 2 problems (THC and CACAO). The gain is obtained by the ratio of the signal to noise of the reconstructed image divided by the signal to noise of the acquisition. In abcissa the random realization samples. Successively with an increasing snr of the acquisition from 102 to 1010 photon per non zero acquisition pixel (ppp).
Even though some fluctuations are clearly visible in the different simulations, there is a clear gap between the two systems. The following Table 4 gives the
Table 4. Average signal to noise ratio gain for THC and CACAO.
mean of all the snrg for both systems.
Figure 24 depicts 10 reconstructed images next to the original pinstripe pattern.
Figure 24. Reconstructed image of a resolution pinstripe pattern by the pseudoinverse method, for the 2 matrices (THC and CACAO) for various number of photons per non zero acquisition pixel (ppp).
6. Discussion
6.1. Condition Number in the Literature
The value of the condition is well described in the inverse problem literature and linear algebra textbooks [10] [13] . The SPECT and PET literature has also recognized and used this tool [14] - [20] . Our results, for example, agree with the work of [19] which shows that a sufficient number of acquisitions angles in THC are necessary to reduce the condition number. These authors showed that the system even becomes rank deficient if the number of projection angles (
6.2. Why Have Not We Used another Performance Index?
The medical imaging literature is full of papers intended to measure the performance or the quality of a tomographic image. Some papers even try to evaluate the usefulness of the images related to a specific task [24] . Some of these performance indices apply to the reconstructed images: we can cite the Standard Deviation [25] or the Contrast Recovery Coefficient (CRC) [26] or the SNR gain [27] . But all these performance measurements do not apply to the same thing. The condition number applies solely to the geometry of the system, meaning, the system direct matrix. With the exception of the last 2 subchapters we did not mention images. The condition number applies whatever the image studied, and in addition applies whatever the reconstruction algorithm used. It is simply an intrinsic property of the transfer matrix. In the last two subchapters we needed to choose an image (pinstripe resolution pattern), a noise distribution and a reconstruction algorithm. In this chapter we use the snrg in a similar manner to [27] . With more hypothesis (the type of lesion to detect in the observer model) we can go further with the specialization, but with a narrower result. This was not the purpose of this article which tries to compare 2 geometries with a minimum of extra hypothesis.
6.3. So, What Does the Results Mean?
In chapter 3 we introduced 2 questions. The first was: Do the photons collected with CACAO carry the same information quality as the photons collected with THC SPECT in terms of location?
If the location were imprecise, the direct matrix would be rank deficient. The fact that the rank of the matrix equals the number of unknowns means that, in the absence of noise, the reconstructed image would be perfect. In linear algebra we say: the matrix has full rank. This result is the consequence of the added linear scan in the acquisition sequence. This ensures an overdetermined linear system. Hence the system is accurate in terms of location (comparable to the THC-SPECT).
We introduced the condition number to evaluate the difficulty of solving an inverse problem, which helped us respond to the second question. The graphs speak for themselves: when the dimension of the system increases and when rotation radius increases, the CACAO project presents a smaller condition number than the THC-SPECT.
6.4. Can the Geometry Explain These Results?
The limited performance of the THC SPECT is probably due to the gaussian shape of the response. In fact it is quite difficult to distinguish the difference between the sum of 2 Gaussians, shoulder to shoulder, from a sole gaussian slightly taller. And when we have to separate a large number of Gaussians of various widths the problem becomes worse. Moreover, these Gaussian responses differ only slightly with the source to collimator distance. On the contrary, the added scanning motion combined with the increased depth of the collimator hole produce responses which are easier to distinguish. This difference leads to the difference in condition number.
People familiar with the difficulty of solving deconvolution problems may find our results strange. Large kernel deconvolutions have a reputation for ill-posedness and large condition number. Several years ago we published a reconstruction algorithm for the CACAO problem with a deconvolution step [6] . A transformed matrix of the system led to a deconvolution problem. Condition number calculations of this transformed matrix led to us abandoning this method. Effectively, the use of the complete and direct response matrix (without a deconvolution step) leads to a better conditioned problem.
The difficulty of the conventional tomographic inverse problem is often underestimated. It is this difficulty which allows us to believe that the approach of the rotating slat [5] may be not optimal. Although this rotating slat can dramatically increase the acceptance angle of the collimator hole (at least in one direction), it needs a double application of the inverse radon transform. Considering the bad conditioning of the inversion of only 1 stage radon transform, we have some doubt as to the quality of the reconstruction. Another quite different approach is the one proposed by Zhang [4] . In this work, the increase of the acceptance angle (referred as cone angle in this article) is very weak: 6˚ for the largest collimator hole considered. In addition, these authors reported that “The blurring of this last collimator hole is too severe to be corrected…”. This may be related to the fact that this article uses a gaussian shaped response, which is hard to deconvolute.
6.5. What Are the Consequences for the Noise Amplification?
Not only, is the condition number related to the geometry of the tomographic model, it is a property of the response matrix of the model. The direct consequence is that for the same


6.6. What Can Be Said about the Simulated Images?
To illustrate this noise amplification, we conducted some simulations. These simulations raise a number of questions. First the choice of the pseudo inverse reconstruction method (unpenalized least square) may be criticized because, as already mentioned, it is not the best method for solving difficult inverse problems. It is known to amplify the noise. It was chosen here for several reasons. First it is a well known method, and intensively theoretically studied. Second it is quick, simple and has great efficacy in exact or near exact data. Everyone can judge it by looking at the simulations with a high number of ppp. Finally every regularized method which would have given better results at low SNR would have needed the choice of a frequency cut-off, a regularization parameter or a stopping criteria for an iterative method. The OSEM (which is the accepted method in emission tomography) not only needs the choice of the number of iterations and the number of subsets, but it has been developed for the THC-SPECT, meaning for a large number of acquisition angles. Such a big number does not hold for CACAO and a comparison based on this algorithm may have been unfair to CACAO. For all these reasons, reinforced by the fact that the condition number has been calculated in the L2 Norm, we chose a least square estimator. A Gaussian noise is then a choice consistent with the least square reconstruction. We are well aware that in emission tomography the noise is better modelled by a Poisson statistic. We chose a 

Figure 23 and Figure 24 show the power of the condition number, predicting a lower snrg for the THC SPECT than for the CACAO project for a large range of SNR at the acquisition level. Table 4 gives a ratio for the 2 snrg of 15.87 compared to 41.84 for the ratio of the condition numbers.
6.7. What Can We Say about Highly Regularized Reconstruction?
Our simple model allows us to go further in the comparison. We can effectively predict the performance of a regularized method. This performance is depicted in Figure 21. The condition number related to a TSVD truncated at the ith
element is given by the ratio:
rid of half the singular values, the THC is preferable. On the contrary, if one wants to collect the maximum amount of detail and precision in the images, and tries to work with more singular values, then the CACAO approach would be preferable. Keeping a large amount of singular values may seem foolish right now, due to the huge uncertainties caused by the use of the thin-hole-collimator. In fact, the CACAO approach implies more collected photons, meaning a better signal to noise ratio at the acquisition level. Moreover, as shown in Figure 22 the point where the curves cross tends to shifts to the left when the size of the image increases. In other words for big data (more realistic) the THC will perform better than CACAO, but only with dramatically strong regularization (e.g. very low spatial resolution).
6.8. And What about Real Systems?
This study was done analytically, with an approximated and simple hypothesis. The attenuation or the scattering of the gamma rays in the body of the patient, or the scattering in the collimator, were not taken into account in this simplified study. We are aware that nowadays advanced methods of reconstruction in SPECT use much more complex models [28] [29] . It should be remembered, however, that the most impairing phenomenon in SPECT is the photon counting noise (sensitivity of a conventional collimator
El Fakhri in [30] has shown that the second most important factor influencing the contrast and the spatial resolution of the images is the collimator response. It is to be noted that our work proposes improvements for both of these factors.
The feeling that scattering would impair the CACAO reconstruction more than the THC reconstruction was opposed to our previous works. Obviously, a bad condition number could magnify the noise more than the signal. Smith [31] has shown that attenuation and scattering degrade the condition number of the SPECT problem. But there is no reason why this phenomena would degrade the CACAO problem more than that of the THC. Faced with the improved condition number at the start, the opposite seems more likely. In fact, regarding our condition number results, all the noise sources (in the patient) impairing conventional THC are expected to be reduced in the CACAO project.
Another point that may be controversial in this study is the lack of a complete 3D calculation. We did not try it due to the time consuming burden of the calculation, added to the complexity of the programming. In addition, this simple 2D calculation allows for a better understanding of the involved phenomenon combined with a simpler calculation, and so is simpler to verify. It also allows a simple analysis of the whole spectrum of singular values. Even without a true 3D study, this article presents an interesting message because we can already project an application of this article in a real 2D experiment with a slit hole.
6.9. The Problem of DOI and High Count Rate
There are 2 physical phenomena which can be predicted as being worse for CACAO than THC. One is the depth of interaction in the detector. Obviously with an angle of 45˚ for the extreme rays 
The other physical limitation is the high count rate which comes directly from the dramatic increase in sensitivity provided by the new collimator. Obviously a lot of gamma ray detectors present a decrease in their performance with increasing count rates. Here again the semiconductor pixellated detector is less subject to deterioration than the large NaI scintillator which could only count one gamma at a time.
6.10. Can We Predict the Future?
This article is purely theoretical and it will not replace a fine Monte Carlo simulation or a real experiment. It is of course difficult to predict the future. Even the result of an experiment does not guarantee the future. We should remember that the first electronic microscope did not provide a better spatial resolution than the existing optical microscope. Today the spatial resolution of the electronic microscope is 104 times smaller. It is also worth mentioning that the neutron, the positron, the rounded shape of the earth and some stars had been theoretically predicted before they were discovered and universally accepted. So we can let the reader believe what they want and we just offer the following Table 5 to sum-up the pros and cons.
Table 5. Pro and cons of CACAO versus THC.
7. Conclusion
The mathematical inverse problem of SPECT with THC is hard to solve. The CACAO project may not only improve the signal to noise ratio at acquisition level, but it may also facilitate the calculation of a good reconstructed image and the use of a more complete set of data. To put it differently, this article seems to demonstrate that the photons recorded by the CACAO project carry better localisation information than that carried by the THC photons. For a low resolution image, with a small image size and a small gyration radius, the THC system is the best method.
Aknowledgements
This study was supported by the “Pays de Loire” MPIA Grant. The authors wishes to thank all the students who have worked on this subject and the colleagues of the UA who have helped us.
Disclosures
No disclosures.
Cite this paper
Jeanguillaume, C., Simonnet, R., Cavaro-Menard, C., Douiri, A., Bouali, I. and Loeb, J.J. (2017) An Alternative Model to Radon Transform for Gamma Ray Emission Tomography. Advances in Molecular Imaging, 7, 13-47. https://doi.org/10.4236/ami.2017.72002
References
- 1. Anger, H. (1957) A New Instrument for Mapping the Distribution of Radio-Active Isotopes. Biology and Medicine Quaterly Report UCRL 3653, 38.
- 2. Radon, J. (1917) Uber die bestimmung von funktionen durch ihre integralwerte langs gewisser mannigfaltigkeiten. Berichte uber die Verhandlungen Gesellshaft der Wissenschaften zu Leipzig. Journal of Mathematical Physics, 69, 262-277.
- 3. Meng, L.J. and Clinthorne, N.H. (2004) A Modified Uniform Cramer-Rao Bound for Multiple Pinhole Aperture Design. IEEE Transactions on Medical Imaging, 23, 896-902.
https://doi.org/10.1109/TMI.2004.828356 - 4. Zhang, B. and Zeng, G.L. (2007) High-Sensitivity Spect Imaging Using Large Collimator Holes and Geometric Blurring Compensation. IEEE Nuclear Science Symposium Conference Record, 6, 4279-4284.
- 5. Lodge, M.A., Webb, S., Flower, M.A., et al. (1996) A Prototype Rotating Slat Collimator for Spect. IEEE Transactions on Medical Imaging, 15, 500-511.
- 6. Jeanguillaume, C., Quartuccio, M., Begot, S., et al. (2002) Emission Tomography with a Large-Hole Collimator (Cacao): A Possible New Way to Improve the Radionuclide Imaging. Journal of Computer Assisted Tomography, 26, 1057-1062.
https://doi.org/10.1097/00004728-200211000-00036 - 7. Jeanguillaume, C., Quartuccio, M., Begot, S., et al. (1996) Gamma camera a collimation assistee par ordinateur (Cacao). Premiere partie: principes de base et methode de reconstruction. RBM, 18, 198-206.
https://doi.org/10.1016/S0222-0776(97)89224-3 - 8. Jeanguillaume, C., Douiri, A., Quartuccio, M., et al. (2001) Cacao a Collimation Means Well Suited for Pixellated Detectors. IEEE Nuclear Science Symposium Conference Record, 4, 2291-2294.
- 9. Jeanguillaume, C., Quartuccio, M., Begot, S., et al. (1996) Gamma camera a collimation assistee par ordinateur (Cacao). Deuxieme partie: une nouvelle approche dans l’etude des performances en tomographie d’emission. RBM, 18, 207-215.
https://doi.org/10.1016/S0222-0776(97)89225-5 - 10. Strang, G. (2009) Introduction to Linear Algebra. 4th Edition, Wellesley-Cambridge Press, Wellesley, MA.
- 11. Barrett, H. and Myers, K. (2003) Foundations of Image Science. John Wiley & Sons, Hoboken New Jersey.
- 12. Seo, Y., Wong, K.H., Sun, M., Franc, B.L., Hawkins, R.A. and Hasegawa, B.H. (2005) Correction of Photon Attenuation and Collimator Response for a Body-Contouring Spect/Ct Imaging System. The Journal of Nuclear Medicine, 46, 868-877.
- 13. Bertero, M. and Boccacci, P. (1998) Introduction to Inverse Problems in Imaging. IOP Publishing Ltd., Philadelphia, PA.
https://doi.org/10.1887/0750304359 - 14. Sun, X., Ma, T. and Jin, Y. (2004) Svd Reconstruction Algorithm in 3d Spect Imaging. Nuclear Science Symposium and Medical Imaging Conference IEEE Conference Record, 6, 3527-3530.
- 15. Usman, M., Hero, A.O., Fessler, J.A. and Rogers, W.L. (1993) Bias-Variance Tradeoffs Analysis Using Univorm Cr Bound for a Spect System. IEEE Nuclear Science Symposium and Medical Imaging Conference Report, 1, 1463-1038.
- 16. Fessler, J.A. and Booth, S.D. (1996) Conjugate-Gradient Preconditioning Methods for Shift-Variant Pet Image Reconstruction. IEEE Transactions on Image Processing, 8, 688-699.
https://doi.org/10.1109/83.760336 - 17. La, V. and Grangeat, P. (1998) Minimal Residual Cone-Beam Reconstruction with Attenuation Correction in Spect. Physics in Medicine & Biology, 43, 715-727.
https://doi.org/10.1088/0031-9155/43/4/002 - 18. Zeng, G.L. and Gagnon, D. (2004) Image Reconstruction Algorithm for a Spect System with a Convergent Rotating Slat Collimator. IEEE Transactions on Nuclear Science, 51, 142-148.
https://doi.org/10.1109/TNS.2003.823042 - 19. Borwein, J.M. and Sun, W. (1997) The Stability Analysis of Dynamic Spect Systems. Numerische Mathematik, 77, 283.
https://doi.org/10.1007/s002110050287 - 20. Jorgensen, A.N. and Zeng, G.L. (2008) Svd-Based Evaluation of Multiplexing in Multipinhole Spect Systems. International Journal of Biomedical Imaging, 2008, Article ID: 769195.
https://doi.org/10.1155/2008/769195 - 21. Tikhonov, A.N. (1963) Solution of Incorrectly Formulated Problems and the Regularization Method. Soviet Mathematics Doklady, 4, 1035-1038.
- 22. Phillips, D.L. (1962) A Technique for the Numerical Solution of Certain Integral Equations of the First Kind. ACM, 9, 84-97.
https://doi.org/10.1145/321105.321114 - 23. Hansen, C. (1987) The Truncated Svd as a Method for Regularization. BIT Numerical Mathematics, 27, 534-553.
https://doi.org/10.1007/BF01937276 - 24. Barrett, H.H., Yao, J., Rolland, P. and Myers, K.J. (1993) Model Observers for Assessment of Image Quality. Proceedings of the National Academy of Sciences of the United States of America, 90, 9758-9765.
https://doi.org/10.1073/pnas.90.21.9758 - 25. Fessler, J.A. (1996) Mean and Variance of Implicitly Defined Biased Estimators (such as Peanlized Maximum Likelihood): Applications to Tomography. IEEE Transactions on Image Processing, 5, 493-506.
https://doi.org/10.1109/83.491322 - 26. Qi, J. (2000) Resolution and Noise Properties of Map Reconstruction for Fully 3d Pet. IEEE Transactions on Medical Imaging, 19, 493-506.
https://doi.org/10.1109/42.870259 - 27. Cao, N., Huesman, R.H., Moses, W.W. and Qi, J. (2010) Detection Performance Analysis for Time-of-Flight Pet. Physics in Medicine and Biology, 55, 6931-6949.
https://doi.org/10.1088/0031-9155/55/22/021 - 28. Soares, E.J., Byrne, C.L., Glick, S.J., Appledorn, C.R. and King, M.A. (1991) Implementation and Evaluation of an Analytical Solution to the Photon Attenuation and Nonstationary Resolution Reconstruction Problem in Spect. IEEE Nuclear Science Symposium Conference Record, 2-9 November 1991, 1789-1796.
https://doi.org/10.1109/NSSMIC.1991.259222 - 29. Beekman, F.J., Eijkman, E.G.J., Viergever, M.A., Borm, G.F. and Slijpen, E.T.P. (1993) Object Shape Dependent Psf Model for Spect Imaging. IEEE Transactions on Nuclear Science, 40, 31-39.
- 30. Elfakhri, G., Buvat, I., Benali, H., Todd-Prokropek, A. and DiPaola, R. (2000) Relative Impact of Scatter, Collimator Response, Attenuation, and Finite Spatial Resolution Corrections in Cardiac Spect. The Journal of Nuclear Medicine, 41, 1400-1408.
- 31. Smith, M.F., Floyd, C.E. and Jaszczak, R.J. (1992) Reconstruction of Spect Images Using Generalized Matrix Inverses. IEEE Transactions on Medical Imaging, 11, 165-175.
https://doi.org/10.1109/42.141640 - 32. He, Z., Li, W., Knoll, G.F., Wehe, D.K. and Stahle, C.M. (2000) Measurement of Material Univormity Using 3-d Position Sensitive Cdznte Gamma-Ray Spectrometers. Nuclear Instruments and Methods in Physics Research A, 441, 459-467.
https://doi.org/10.1016/S0168-9002(99)00860-8 - 33. Salcin, E., Barrett, H.H., Barber, H.B., Takeda, S., Watanabe, S., Takahashi, T. and Furenlid, L.R. (2014) Fisher Information Analysis of Depth-of-Interaction Estimation in Double-Sided Strip Detectors. IEEE Transactions on Nuclear Science, 61, 1243-1251.
https://doi.org/10.1109/TNS.2014.2317454 - 34. Montemont, G., Lux, S., Monnet, O., Stanchina, S. and Verger, L. (2012) Evaluation of a Czt Gamma-Ray Detection Module Concept for Spect. IEEE Nuclear Science Symposium and Medical Imaging Congress Conference Report, 27 October-3 November 2012, 4091-4097.
https://doi.org/10.1109/NSSMIC.2012.6551935



























