Journal of Transportation Technologies
Vol.06 No.02(2016), Article ID:63424,15 pages
10.4236/jtts.2016.62006
Calibration of Car-Following Models Considering the Impacts of Warning Messages from Tablet/Smartphone Application
Qing Li, Fengxiang Qiao, Lei Yu
Innovative Transportation Research Institute, Texas Southern University, Houston, TX, USA
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 December 2015; accepted 13 February 2016; published 16 February 2016
ABSTRACT
The phenomenon of car-following is special in traffic operations. Traditional car-following models can well describe the reactions of the movements between two concessive vehicles in the same lane within a certain distance. With the invention of connected vehicle technologies, more and more advisory messages are in development and applied in our daily lives, some of which are related to the measures and warnings of speed and headway distance between the two concessive vehicles. Such warnings may change the conventional car-following mechanisms. This paper intends to consider the possible impacts of in-vehicle warning messages to improve the traditional car-following models, including the General Motor (GM) Model and the Linear (Helly) Model, by calibrating model parameters using field data from an arterial road in Houston, Texas, U.S.A. The safety messages were provided by a tablet/smartphone application. One exponent was applied to the GM model, while another one applied to the Linear (Helly) model, both were on the stimuli term “difference in velocity between two concessive vehicles”. The calibration and validation were separately conducted for deceleration and acceleration conditions. Results showed that, the parameters of the traditional GM model failed to be properly calibrated with the interference of in-vehicle safety messages, and the parameters calibrated from the traditional Linear (Helly) Model with no in-vehicle messages could not be directly used in the case with such messages. However, both updated models can be well calibrated even if those messages were provided. The entire research process, as well as the calibrated models and parameters could be a reference in the on-going connected vehicle program and micro/macroscopic traffic simulations.
Keywords:
Car-Following Model, Smartphone, Tablet, Warning Messages, Connected Vehicles

1. Introduction
1.1. Background of Research
Car-following is a special process in traffic operation where a following vehicle adjusts its accelerations based on the performance of the leading vehicle(s) and current status of the following vehicle. Car-following behaviors have been carefully studied with the first generation of models initiated in earlier 1950s [1] [2] . Since then, many types of car-following models have been proposed, most of which were based on the assumption that each driver reacts to a stimulus from the vehicle(s) ahead (called the leading vehicle(s)) [3] . Some car-following models regard vehicles as moving particles [4] [5] .
Car-following models are one of the core processes of almost all microscopic traffic simulation models, including FRESIM, NETSIM, INTEGRATION, and CARSIM [6] . It is very important in traffic flow theory, and has been widely used in safety analyses and traffic operations [7] [8] , as well as in vehicle emission estimations [9] .
The headway distance is an important variable in car-following models, the inverse of which is density. With this and other linkages, the car-following models can be used to bridge macroscopic with microscopic traffic flow analyses as well to characterize not only the behaviors of individual vehicle, but also the overall relationships among traffic flow variables, such as volume, speed, and density [10] [11] .
Factors that may impact car-following behaviors include driver’s psychological and physical status, the level of service of the roadway, and vehicle’s performance [12] . Any change or influence of these factors could apparently alter the car-following process, resulting in revised parameters in car-following models or would even invalid them.
Recently, with the invention of many innovative technologies, The United States Department of Transportation (USDOT) initiated a Connected Vehicle (CV) program to develop a platform combining well-defined technologies, interfaces, and processes to minimize risks and enhance the overall performance of traffic operations. It includes the Connected Vehicle Human Factors Research focusing on “understanding, assessing, planning for, and counteracting the effects of signals or system-generated messages that take the driver’s eyes off the road (visual distraction), the driver’s mind off the driving task (cognitive distraction), and the driver’s hands off the steering wheel (manual distraction)” [13] .
Before drivers’ hands are “fully off”, the prompted messages from the CV system are actually additional stimuli to drivers, which would definitely affect driving behaviors as well as the resulted car-following behaviors. This creates a challenge on how to incorporate the impacts of such supplementary warning messages into traditional car-following models.
1.2. Research Objectives
The objective of this paper is to improve the traditional car-following models by considering the impacts of in- vehicle warning messages from tablet/smartphone applications within a CV system. The parameters of the improved models would be re-calibrated using field test data.
2. Warning Messages with Connected Vehicles
A CV system relies on wireless communications and/or other innovative technologies to detect/identify the presence of surrounding vehicles, pedestrians, bicycles, and other objects nearby, and provide drivers with corresponding messages to enhance the mobility, safety, and air quality [14] -[16] .
The effects of the corresponding messages on driving behaviors have been studied in different situations, such as smart warning messages at a work zone advance warning area [17] -[19] and activity area [20] , and the messages for pedestrian crossings [21] , STOP sign intersection [22] , and traffic signals at intersections [23] [24] . These messages could be provided by Dedicated Short Range Communication (DSRC) technologies using a dedicated device such as the Radio Frequency Identification (RFID) [25] , a tablet/smartphone application [26] , etc.
These in-vehicle warning messages are usually in either audio or visual forms to notify drivers on driving speed [27] , headway distance, headway time, careful notification, rear-front distance, or the speed of the front vehicle [28] . The car-following mechanism is illustrated in Figure 1(a), while the corresponding messages for different emergent situations are depicted in Figure 1(b). The specific definition of the timing messages, including

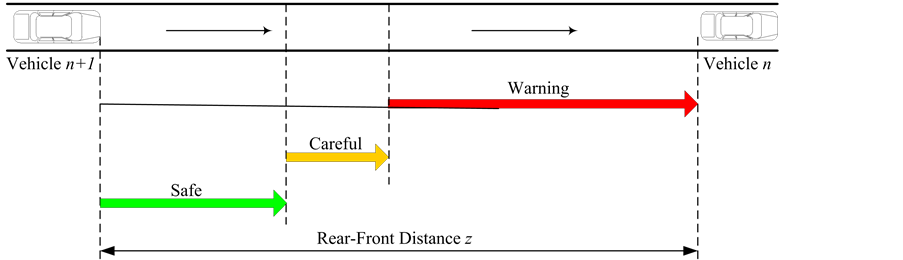
Figure 1. (a) Illustration of reactions between two adjacent vehicles during a car-following scheme; (b) Messages provided from a tablet/smartphone on the 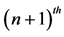 following vehicle.
following vehicle.
a safe message, a careful message, and a warning message in Figure 1(b) could vary, but there is a marginal distance for the timing to provide a warning message. Drivers are supposed to at least receive a warning message before they are able to stop on time without conflicting with the front vehicle.
3. Existing Car-Following Models and the Incorporation of In-Vehicle Messages
3.1. Interaction between Two Adjacent Vehicles and Types of Car-Following Models
In a car-following situation illustrated in Figure 1(a), the leading vehicle moves at a velocity of  or
or  and acceleration
and acceleration 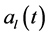 or
or , while the following vehicle moves at a velocity of
, while the following vehicle moves at a velocity of  or
or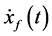 . The acceleration of the following vehicle at time
. The acceleration of the following vehicle at time  is
is  or
or , and the rear-front distance between the two vehicles is z. With the vehicle length notated as L, the headway distance Dx in Figure 1(a) is then calculated as:
, and the rear-front distance between the two vehicles is z. With the vehicle length notated as L, the headway distance Dx in Figure 1(a) is then calculated as: . Car-following models describe the relations among these and some other related variables.
. Car-following models describe the relations among these and some other related variables.
From the engineering view, there are basically five types of car-following models [3] [29] : 1) The Gazis- Herman-Rothery (GHR) models, or named as General Motors (GM) models, which examine the relationships between the following vehicle’s acceleration and other variables [30] [31] ; 2) The linear (Helly) models, which describe the following vehicle’s acceleration as a linear function of the difference in velocity between two concessive vehicles, and the difference in headway and desired following distance [32] [33] ; 3) the safety distance or collision avoidance (CA) models, which seek to specify a safe headway for collision avoidance, assuming that the leading vehicle would act “unexpectedly” [34] ; 4) the psychophysical or action point models (AP), which believe that the driver of the following vehicle would be able to sense the rear-front distance, primarily based on the apparent size change of the leading vehicle [35] [36] ; 5) fuzzy logic-based models, which create fuzzy rules to describe the relationships between acceleration and other related variables, some fuzzifying other types of models including the GM models [37] [38] .
From the view of statistical physics, vehicles can be regarded as a moving particle [5] . Such concepts were reflected in: 1) optimal velocity models [39] ; 2) intelligent driver models [40] ; and 3) cellular automata (CA) models [41] [42] .
Among the above mentioned models, the GM models and the linear (Helly) models are probably one of the most traditional models. In the rest of this paper, these two types of models are further updated by incorporating the impacts of advance warning messages from a tablet/smartphone application.
3.2. Revised GM Car-Following Models Considering Impacts of Warning Messages
GM models are perhaps the most famous class of car-following models with its first version dated more than 60 years ago. It is based on an intuitive hypothesis of “stimuli-reaction” philosophy that a driver receives a “stimulus” (the difference of velocity 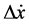 between the leading and following vehicle) at time (t) and react at
between the leading and following vehicle) at time (t) and react at 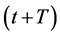 by accelerating at a rate of
by accelerating at a rate of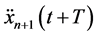
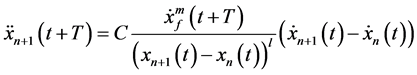
where 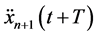
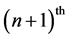
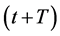

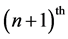
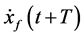

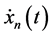
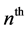
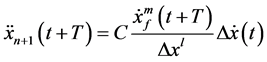
where 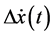
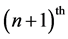
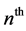
In Equation (2), the sensitivity factor is expressed as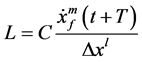
The prevalent use of in-vehicle messages could be additional “stimuli” to drivers, which possibly impacts drivers’ reaction and should be involved into the “stimuli” portion 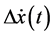
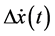

The additional parameter k as well as the coefficient c, could be calibrated using observed data in the case that safety messages are provided.
3.3. Revised Linear (Helly) Model Considering Impacts of Warning Messages
Traditionally, the so-called linear car-following model is referred to the Helly model [3] , the simplified version of which is in Equation (4).
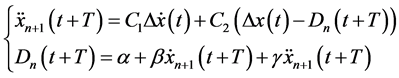
Here, 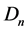
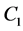
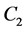
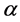
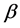

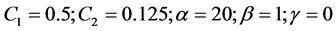
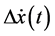
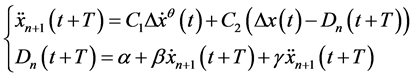
where, θ reflects the impacts of warning messages and should be re-calibrated together with the associated parameter 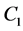
4. Data Collection and Processing
4.1. Test Route
In order to obtain the real data for parameter calibration of the aforementioned revised models, field tests were conducted along an arterial road in Houston, Texas, USA. in June, 2015 during the afternoon non-peak hours (12:00 pm to 4:00 pm). In the test route shown in Figure 1(a), test vehicles departed from intersection A (Bellaire Blvd. @ Gessner St.) towards intersection B (Bellaire Blvd. @ S. Rice St. B), and then made U-turn back to the starting point for a complete circle (i.e., the dashed route in Figure 2(a)). The length between intersections
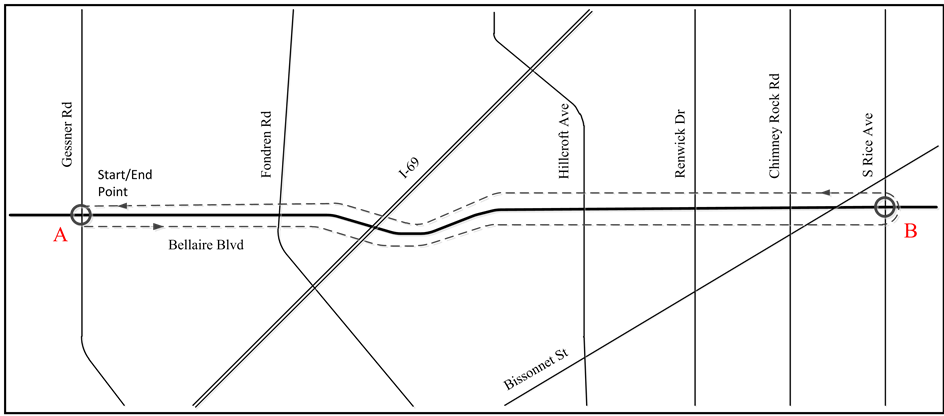

Figure 2. (a) The test route; (b) The tablet and camera placed inside the following vehicle.
A and B is 6.9 km (4.3 miles), namely 13.8 km (8.6 miles) long for each complete test round.
There are 10 traffic signals between intersections A and B in Figure 2(a), which induced frequent accelerations and decelerations. During the test, one vehicle (the following vehicle) was following a specific leading vehicle for a total of four rounds: the first two rounds with the tablet in-vehicle messages, and the rest without such messages.
4.2. Equipment and Devices
The leading vehicle was a 2014 Toyota Corolla and the following vehicle was a 2012 Toyota Camry. The same drivers were employed for the leading vehicle and following vehicle, respectively throughout the test. Dedicated test devices (see Figure 2(b)) included: 1) the Global Positioning System (GPS) on both of the leading vehicle and following vehicle; 2) an On-Board Diagnostics (OBD) II scanning device connected to an in-vehicle computer placed in the leading vehicle to record real time vehicle activity, such as velocity and acceleration rate; 3) a seven-inch screen tablet with an application providing safety messages as is illustrated in Figure 1(b), which was attached to the windshield of the following vehicle; and 4) a camera inside the following vehicle to record all reading displays on the tablet screen.
4.3. Tablet Messages
A tablet application, which can also function in any smartphones, was used to provide an audio and visual alarm for “Careful” and “Warning” distance as shown in Figure 1(b). The velocity of the following vehicle was displayed on the top left of the screen with colored readings representing different safety status. A green background of velocity signified a safe status, while a yellow and red indicated the message of “careful” and “warning”, respectively.
Next to the velocity display there was a reading of the rear-front distance z between the leading vehicle and the following vehicle, which was measured by the tablet application through the image from the back camera of the tablet. Such a distance was displayed with black text within a colored box on the screen. Still, the color represents relevant safety status.
Once the tablet application detects that the time to collision is within 4.0 seconds, the full screen of the tablet would become all yellow with a text message “Careful” for one second together with a short sound alarm. If the time to collision estimation is within 3.0 seconds, the tablet screen would become all red with a text “Warning” for one second also with a sound alarm prompted. The readings of velocity would change their corresponding colors after the full screen “Careful” or “Warning” messages disappeared, but the time to collision could still be within the mentioned margins above.
4.4. Data Collection and Post-Recording
There were three types of information recorded during the on-road test: 1) the velocity of leading vehicle from its OBD II scanner; 2) the GPS data recording both vehicles’ geo-locations at a sampling rate of 10 Hz (10 records per second); and 3) recorded video of tablet images from the camera inside the following vehicle. For the test rounds with no safety messages, the tablet kept silent and placed at a location where the driver could neither see nor hear any safety message. However, the following vehicle’s speed and rear-front distance displayed on tablet screen were still recorded by the camera.
After the field test, the collected raw information was post-processed in the lab. The speed of following vehicle, rear-front distance, and instant “Careful (Yellow)” and “Warning (Red)” messages were retrieved from the videos of tablet interface at a sampling rate of 1 Hz.
4.5. Data Processing
All types of recorded data for both the leading and following vehicles were synchronized based on the time from both GPSs. Data quality was controlled to eliminate the outlier in each data set. The velocity of the leading vehicle from OBD II scanner, which was collected at an uneven sampling rate of a little bit more than 1 second, was interpolated into the evenly distributed second-by-second data.
Each prepared data pair included: 1) acceleration rate of the following vehicle; 2) velocity of the following vehicle; 3) rear-front distance between the leading vehicle and the following vehicle; 4) velocity of the leading vehicle; and 5) time recorded in second.
The recorded data were sorted into four major groups: 1) deceleration period when approaching intersection without messages, 2) deceleration period when approaching intersection with safety messages, 3) acceleration period when leaving intersection without messages, and 4) acceleration period when leaving intersection with safety messages.
A total of 226 sets of data pairs were prepared from the field observations. For deceleration scenario, there were 40 data pairs for without and 68 pairs for with in-vehicle messages; while for acceleration scenario, there were 60 and 58 data pairs prepared for without and with messages, respectively.
5. Scan of Following Vehicle’s Acceleration Rates with and without Safety Messages
Figure 3 is the box plot of deceleration/acceleration rates with and without safety messages, which shows that with the safety messages, the vehicles decelerated much harder than without message (see Figure 3(a))
(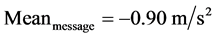
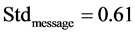
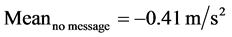
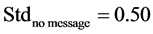
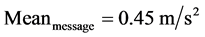
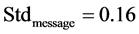
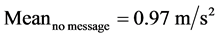
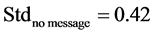
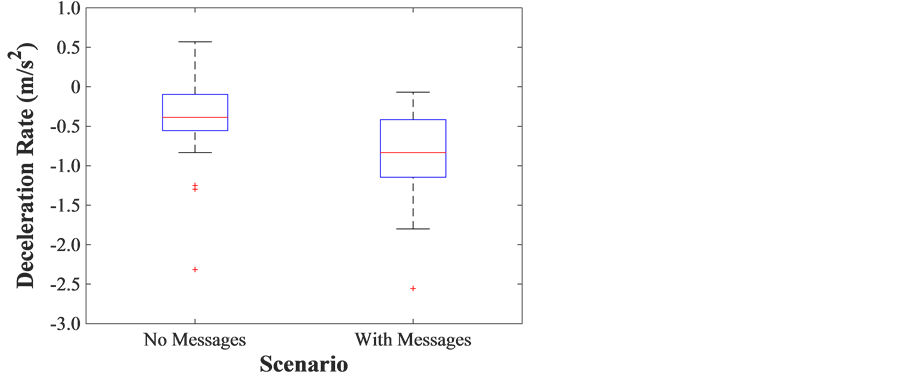

Figure 3. Comparison of (a) deceleration and (b) acceleration rates with and without safety messages.
The single factor ANOVA test indicated that, the difference in deceleration rates with and without safety messages were significant (F (1, 68) = 13.3, p = 5.2E−4), and the difference in acceleration rates with and without safety messages were significant as well (F (1, 30) = 21.2, p = 7.1E−5). The statistically significant differences are consistent with the mentioned assumption of the change in car-following behaviors.
6. Calibration of Parameters for Revised Car-Following Models
6.1. Calibration and Analytical Procedure
The revised GM model and Linear (Helly) model would be calibrated using the collected field data. The calibration and examination process is composed of the following steps.
Step 1. Applying parameters from literature. The collected field data, including both without message and with messages, were first used to calculate the acceleration of leading vehicles using parameters from literatures based on existing car-following models in Equations ((2) and (4)).
Step 2. Self-calibrating parameters using field data. The parameters in the existing car-following models Equations ((2) and (4)) were calibrated using the set of data for both with and without safety messages (i.e. calibrating parameters C, m, l in Equation (2), and parameters C1, C2, 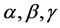
Step 3. Calibrating new parameters with message. The parameters k and C in the revised GM model in Equation (2), and the parameters θ and C1 in the revised Linear (Helly) model in Equation (4) were calibrated using the data set with safety messages. The other parameters in these two equations were from the calibration using data with no message in step 2.
Step 4. Validating revised models using additional data with messages. Additional set of field data with safety messages were used to validate the revised models with additional parameters from Step 3 and the rest parameters from Step 2.
Step 5. Examining modeling and validation errors from all above steps. The accelerations from all above steps were compared with the field observations. The Normalized Route Mean Square Error (NRMSE) and the Pearson correlation coefficients were used to compare the goodness of models.
The NRMSE in Step 5 is calculated based on Equation (6).

where, 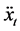
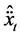
6.2. Calibration of Revised GM Model
At the first step, the parameters of the Ozaki’s GM car-following model [24] were used to calculate the deceleration/acceleration rates. This relatively newer model separates the situations of deceleration and acceleration. Its optimum parameter combinations are: c = 1.1, m = 0.9, and l = 1 for deceleration, and c = 1.1, m = −0.2, and l = 0.2 for acceleration.
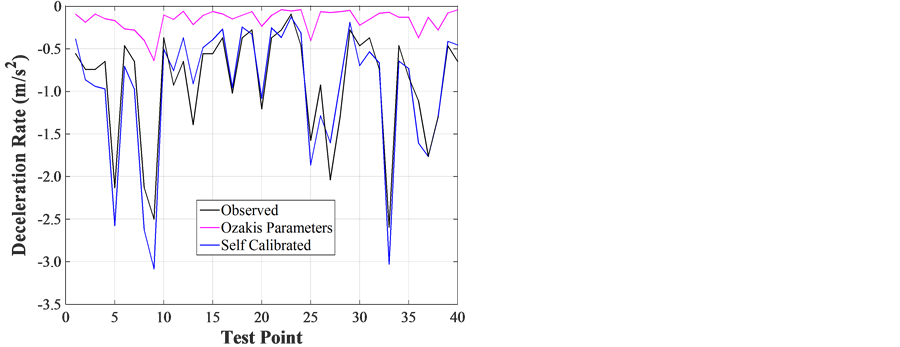
Table 1 lists the calibrated parameters of revised GM models for deceleration and acceleration cases. Using the Ozaki’s parameters, there is a higher NRMSE (38.2%) and a relatively lower correlation coefficient R (0.51) (column a) as is expected since the parameters were calibrated from a different test conducted in 1993. The self-calibrated parameters (m = −0.54 and l = 1.48) using the traditional GM model in Equation (2) from the collected field data with no safety messages, resulted in a better NRMSE (10.6%) and a highly correlation relationship (R = 0.95) (column b). The visual comparisons of the calibrated results are shown in Figure 4(a) and Figure 4(c).
In Figure 4(a), the estimated deceleration rates by the self-calibrated parameters using the traditional GM model (the blue line) fits much better to the observed values (the black line), whereas the ones based on Ozaki’s parameters (the magenta line) yield bigger differences even though it can basically catch the trend.
For the scenarios with warning messages, 28 of 60 data pairs were reserved for validation, while 40 data pairs were used for calibration. Table 1 also lists results on the direct use of Osaki’s parameters for the collected data
Table 1. Calibrated parameters for revised GM models.
a. Ozaki, 1993; b. The results that direct use Ozaki’s parameters; c. Calibrated parameters results from the scenarios with no message; d. Calibrated k results using revised Equation (3).
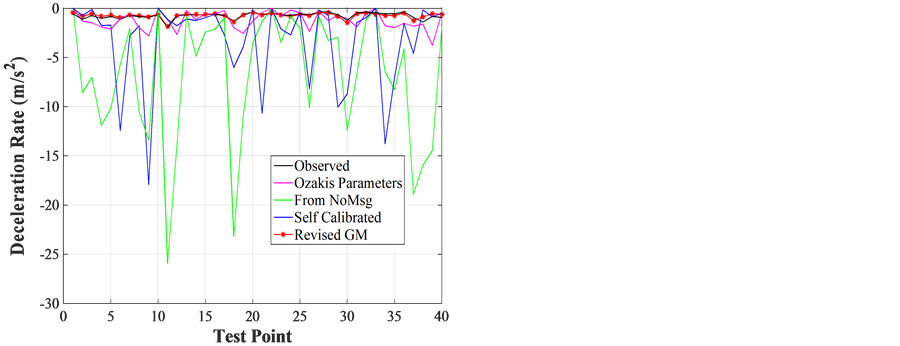
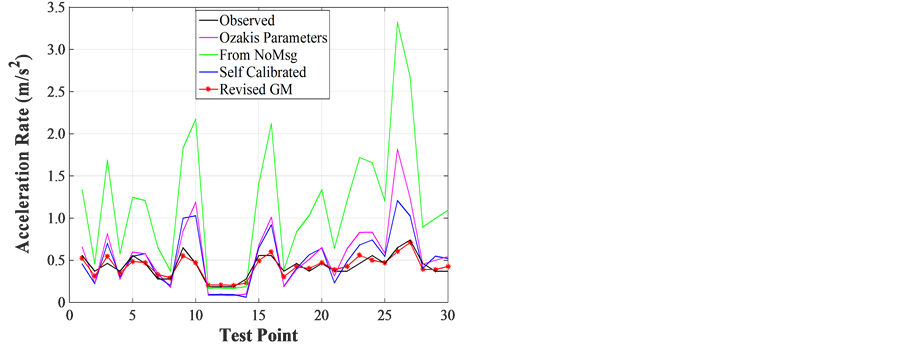
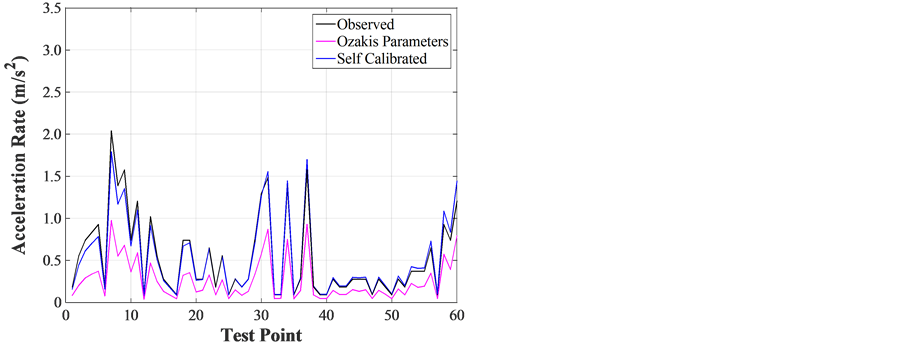
Figure 4. (a) Deceleration with no safety message; (b) Deceleration with safety messages; (c) Acceleration with no safety messages; (d) Acceleration with safety messages.
with safety messages. The resulted NRMSE (63.1%) and R (0.24) is not the indicator of a good fit to the observed data. The deceleration rates from this set of parameters are indicated as the magenta line in Figure 4(b). It is noticed that the predicted values by revised GM model (the red line) matches better to the observed data (the black line).
Column (d) in Table 1 is the results with self-calibrated parameters (m = 4.32 and l = 13.04) using Equation (2) based on the field data with messages, NRMSE (318.3%) and R (0.16) for deceleration. This implies that the traditional GM model in Equation (2) may not be able to fully fit to the real deceleration data, even after calibration. Column (e) in Table 1 (a) is the results still from Equation (2) but using the same parameters in column (b) (m = −0.54 and l = 1.48, which were calibrated from field data with no message for deceleration), and based on the field data with messages. The calculated deceleration rates under this situation are represented by the green line in Figure 4(b), which shows the biggest errors of the model estimations (NRMSE 554.3% and R = 0.76 in column (e) for deceleration). This denotes that, due to the impacts of safety messages, the parameters calibrated from no message data may not be optimum for the estimation.
The calibration results in column (f) are for the revised GM model in Equation (3). The added parameter k was calibrated together with C1 based on the field data with messages. Other parameters were still from column (b) with m (−0.54) and l (1.48). Magically, the NRMSE is 10.4% and R is 0.86 for deceleration, both are in the acceptable ranges. This tells that, the revised GM model could possibly reflect the car-following mechanism with the presence of safety messages in a deceleration situation. This is also reflected as the red line in Figure 4(b) that fits the field data (the black line) very well.
The calculation and calibration for the process of acceleration is pretty similar to the one for deceleration. The calibrated parameters and associated indexes are listed in Table 1 in the second half rows for accelerations, while the acceleration rates under different comparing situations are plotted in Figure 4(c) and Figure 4(d).
In column (a) and (b) and Figure 4(c) for the situation with no safety message under acceleration, the self- regressed parameters (m = 0.11 and l = 0.49) can yield better fits to the observed acceleration rates, (NRMSE 4.17% and R 0.99 for acceleration), while the Ozaki’s parameters bring good R 0.98, but not very small NRMSE 18.5%.
In columns (c) to (f) and Figure 4(d) for the situation with safety messages under acceleration, the best fit is the revised GM model in column (f) with NRMSE 8.9% and R 0.93. In this case, the parameters are m = 0.11, l = 0.49, and k = 0.36. However, the NRMSE and R values for other cases in columns (c) to (e) are also acceptable with the NRMSEs 39.5% - 57.8% and R-values around 0.82 - 0.86. This means that the impacts of safety messages for acceleration part are not as significant as those for deceleration part. However, the revised GM model could significantly reduce the modeling errors from 39.5% (from self-calibration by GM model) to 8.9% (from revised GM model), in terms of the NRMSE.
6.3. Calibration of Revised Linear (Helly) Model
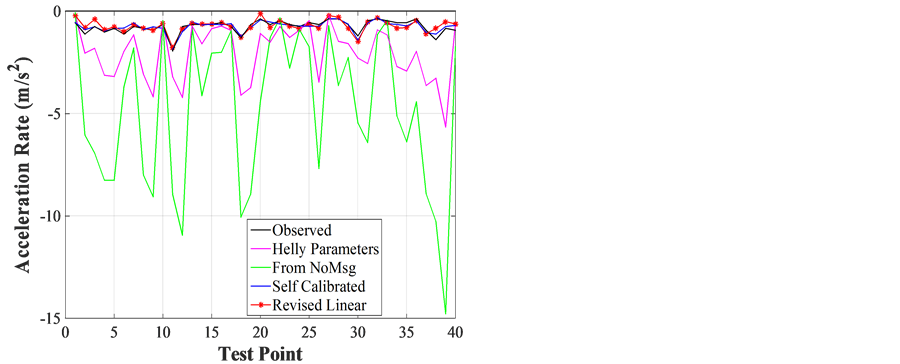
The calculation and calibration of the revised linear (Helly) model for the process of deceleration and acceleration are listed in Table 2 and illustrated in Figure 5.
For the deceleration cases with no messages, the NRMSE14.3% and R0.83 for self-calibrated parameters in column (b) are better than the direct use of Helly’s parameters in column (a) (NRMSE 41.0% and R 0.08). For the deceleration cases with safety messages, both the self-calibrated from Helly’s model in column (d) and calibrated from revised Helly’s model in column (f) provides better fits of deceleration rates with NRMSEs being 8.6% and 11.98%, respectively, and R values being 0.90 and 0.83, respectively. They are much better than the other two situations in columns (c) and (e). The greatest NRMSE 341.9% is in column (e), which further indicates the significant impacts of safety messages on deceleration rates as having been discussed for the GM model. These are also reflected in the multiple plots of deceleration rates in Figure 5(b).
Still, the traditional Linear (Helly) Model in Equation (4) can adopt the situation with safety messages for deceleration (NRMSE = 8.6% in column (d)). In the meantime, the revised Linear Model in Equation (5) can do well also (NRMSE = 11.98% and R = 0.83 in column (f)). The best-fit parameters for Linear (Helly) model are: c1 = 0.01, c2 = 7.4E−4, α = 1.53, β = −0.06, γ = −0.14. The calibrated parameters for the revised Linear (Helly) Model are: c1 = 0.48, c2 = 0.04, α = 1.64, β = −0.02, γ = −0.11, and θ = 0.12.
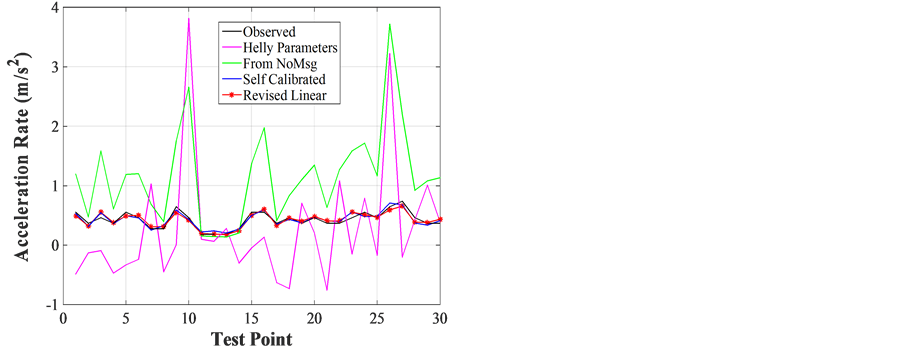
For the acceleration cases, similar to the revised GM model for the acceleration situation with no message (column (a) and (b)), the self-calibrated Linear (Helly) Model provides better fit to the acceleration rates
Table 2. Calibrated parameters for revised linear (Helly) models.
a. Using Helly’s parameters directly; b. B. Calibrated parameters results from the scenarios with no message; c. Calibrated θ results using revised Equation (5).
(NRMSE 5.13% and R 0.98) than directly using the parameters from the traditional Linear (Helly) Model (NRMSE 54.4% and R 0.45). This can also be observed in Figure 5(c) for acceleration rates from Helly’s parameters (the magenta line) and from the self-calibrated parameters (the blue line) using the field data with safety messages.
For the revised GM model for the acceleration situation with messages (column (c) to (f)), the best cases are still for the self-calibrated parameters using the Linear model (column (d) with NRMSE = 8.6%, R = 0.94), and for the use of the revised Linear Model (column (f) with NRMSE = 9.05%%, R = 0.93). Similarly, the higher NRMSE (179.7%) in column (e) indicates the significant impacts of safety messages on acceleration rates.
The best-fit parameters for the Linear (Helly) Model for acceleration process are: c1 = 0.10, c2 = −0.01, α = −0.45, β = −0.01, and γ = −0.03, while the calibrated parameters for the revised Linear (Helly) Model are: c1 = 0.37, c2 = −0.01, α = −0.19, β = −0.01, γ = −0.02, and θ = 0.37.
6.4. Validation of Both Revised Models
The traditional and revised GM model and Linear (Helly) model were further validated with the parameters in Table 1 and Table 2 using additional field data sets. Twenty-eight data pairs under deceleration situation were employed to validate both the revised GM Model and the revised Linear (Helly) Model. Another 28 data pairs under acceleration situation were employed to validate both models. The validation results are listed in Table 3 in terms of NRMSE and R for the fits to the observed deceleration/acceleration rates.
In Table 3, the validated NRMSEs for both revised models under deceleration and acceleration situations range from 5.5% to 15.4%, and R values from 0.87 to 0.93. This means these two revised models can still perform well even with additional validated data sets. The best-fit parameters, which have been calibrated and validated for the traditional and revised GM and Linear (Helly) models, are summarized in Table 4.

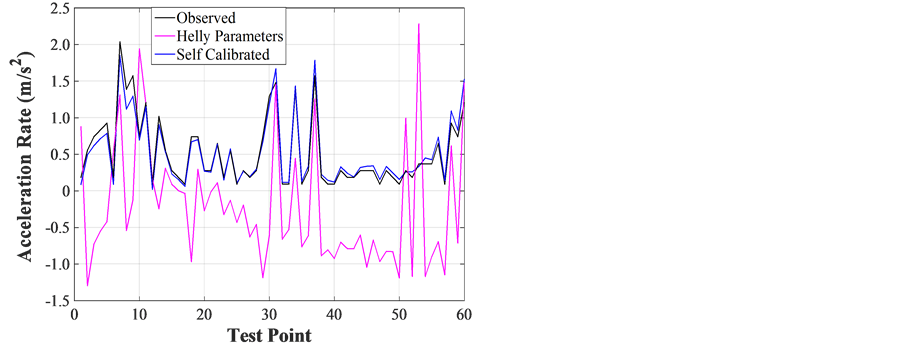
Figure 5. (a) Deceleration with no safety message; (b) Deceleration with safety messages; (c) Acceleration with no safety messages; (d) Acceleration with safety messages.
Table 3. Validation results of revised GM models and linear (Heely) model with messages.
In Table 4, the parameters of traditional and revised GM models are for Equations ((2) and (3)), while the parameters of traditional and revised Linear (Helly) Models are for Equations ((4) and (5)). In Table 4, no parameters are provided for the two blocks with safety messages (marked as N/A). This is because the traditional GM model could not provide good calibrated parameters in this situation. In the case with no safety message, the revised models would become vestigial to the traditional GM and Linear (Helly) Models by setting the added parameters k1.0 and θ1.0, respectively.
7. Conclusions
In this paper, two types of car-following models, the GM model and the Linear (Helly) model, were re-calibrated and revised using the field data collected in Houston, Texas, U.S.A. so as to characterize the impacts of safety messages from a tablet application. Both revised GM model and revised Linear (Helly) model
Table 4. Overview of the best fit parameters of traditional and revised GM and Linear (Helly ) models.
were proposed by applying additional exponents to the stimuli term “the different of velocity between a leading vehicle and a following vehicle”. A part of the field data was used to calibrate the parameters of the traditional and revised GM model and Linear (Helly) model, while the others were for validation.
Calibration results showed that, when the safety messages from a tablet application were provided, the GM model failed to properly fit in the field car-following data, even a calibration process had been applied for both deceleration and acceleration situations. The calibrated parameters in the cases with no message for the Linear (Helly) Model should not be directly applied to the car-following data with safety message. A calibration to either the Linear (Helly) Model or the revised Linear (Helly) Model is necessary for a better fit.
Both calibration and validation results demonstrated that, the safety messages did affect the calibration of parameters of car-following models for both deceleration and acceleration situations. The entire research process, the revised car-following models, and the calibrated parameters could be good references to the on-going connected vehicle program, the development of drivers’ safety messages, as well as the traffic simulations in both microscopic and macroscopic scales.
Acknowledgements
The authors acknowledge that this research is supported in part by the Tier 1 University Transportation Center TranLIVE#DTRT12GUTC17/KLK900-SB-003, and the National Science Foundation (NSF) under grants #1137732. The opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the funding agencies. The authors would like to appreciate Yijun Qiao and Jinghong Ma in shaping the initial idea and part of the data collections.
Cite this paper
QingLi,FengxiangQiao,LeiYu, (2016) Calibration of Car-Following Models Considering the Impacts of Warning Messages from Tablet/Smartphone Application. Journal of Transportation Technologies,06,61-75. doi: 10.4236/jtts.2016.62006
References
- 1. Reuschel, A. (1950) The Movement of a Column of Vehicles when the Leading Vehicle Is Uniformly Accelerated or Decelerated. (Fahrzeugbewegungrn in der Kolonnebeigleichfoermigbeschleunig]-tem oderverzoegertemLeifahrzeug). Magazine of the Austrian Engineer and Architect Association (Zeitschrift des Österreichischen Ingenieurund Architekten-Vereine), 95, 59-62, 73-77.
- 2. Pipes, L.A. (1953) An Operational Analysis of Traffic Dynamics. Journal of Applied Physics, 24, 274-281.
http://dx.doi.org/10.1063/1.1721265 - 3. Brackstone, M. and McDonald, M. (1999) Car-Following: A Historical Review. Transportation Research Part F: Traffic Psychology and Behavior, 2, 181-196.
http://dx.doi.org/10.1016/S1369-8478(00)00005-X - 4. Weng, Y. and Wu, T. (2002) Car Following Models of Vehicular Traffic. Journal of Zhejiang University-SCIENCE, 3, 412-417.
http://dx.doi.org/10.1631/jzus.2002.0412 - 5. Toledo, T. (2007) Driving Behavior: Models and Challenges. Transportation Reviews, 27, 65-84.
http://dx.doi.org/10.1080/01441640600823940 - 6. Papacostas, C.S. (2001) Transportation Engineering and Planning. 3rd Edition, Prentice Hall, Delhi.
- 7. Luo, L.H., Liu, H., Li, P. and Wang, H. (2010) Model Predictive Control for Adaptive Cruise Control with Multi-Objectives: Comfort, Fuel-Economy, Safety and Car-Following. Journal of Zhejiang University-SCIENCE A (Applied Physics and Engineering), 11, 191-201.
http://dx.doi.org/10.1631/jzus.a0900374 - 8. Tordeux, A., Lassarre, S. and Roussignol, M. (2009) An Adaptive Time Gap car Following Model. Transportation Research Part B: Methodological, 44, 1115-1131.
- 9. Song, G., Yu, L. and Geng, Z. (2015) Optimization of Wiedemann and Fritzsche Car-Following Models for Emissions Estimation. Transportation Research Part D: Transport and Environment, 34, 318-329.
http://dx.doi.org/10.1016/j.trd.2014.11.023 - 10. Jin, S., Wang, D.H., Huang, Z.Y. and Tao, P.F. (2011) Visual Angle Model for Car-Following Theory. Physical A: Statistical Mechanics and Its Applications, 390, 1931-1940.
http://dx.doi.org/10.1016/j.physa.2011.01.012 - 11. Ni, D. Chapter 19 of Traffic Flow Theory: A Unified Perspective.
http://people.umass.edu/ndh/TFT/Ch19%20Bridge.pdf - 12. Rahman, M., Chowdhury, M., Khan, T. and Bhavsar, P. (2015) A Parameter Estimation and Calibration Method for Car-Following Models. IEEE Transactions on Intelligent Transportation Systems, 16, 2687-2699.
http://dx.doi.org/10.1109/TITS.2015.2420542 - 13. United States Department of Transportation (DOT) (2015) Connected Vehicle Research in United States.
http://www.its.dot.gov/connected_vehicle/connected_vehicle_research.htm - 14. Li, Q., Qiao, F. and Yu, L. (2015) Will Vehicle and Roadside Communications Reduce Emitted Air Pollution? International Journal of Science and Technology, 5, 17-23.
- 15. Li, Q., Qiao, F. and Yu, L. (2016) Vehicle Emission Implications of Drivers Smart Advisory System for Traffic Operations in Work Zones. Journal of Air & Waste Management Association. (in press)
http://dx.doi.org/10.1080/10962247.2016.1140095 - 16. Li, Q., Qiao, F. and Yu, L. (2015) Socio-Demographic Impacts on Lane-Changing Response Time and Distance in Work Zone with Drivers’ Smart Advisory System. Journal of Traffic and Transportation Engineering (English Edition), 2, 313-326.
http://dx.doi.org/10.1016/j.jtte.2015.08.003 - 17. Qiao, F., Jia, J., Yu, L., Li, Q. and Zhai, D. (2014) Drivers’ Smart Assistance System Based on Radio Frequency Identification. Transportation Research Record: Journal of Transportation Research Board, 2458, 37-46.
http://dx.doi.org/10.3141/2458-05 - 18. Li, Q., Qiao, F. and Yu, L. (2015) Fuzzy Lane-Changing Models with Socio-Demographics and Vehicle-to-Infra- structure System Based on a Simulator Test. Journal of Ergonomics, 5, 1000144.
- 19. Li, Q., Qiao, F. and Yu, L. (2014) Impacts of Vehicles to Infrastructure Communication Technologies on Vehicle Emissions. Proceedings of the International Conference on Environmental Science and Technology, American Academy of Sciences, Houston, 9-13 June 2014, Paper #: 946.
- 20. Rahman, R., Qiao, F., Li, Q., Yu, L. and Kuo, P.-H. (2015) Smart Phone Based Forward Collision Warning Message in Work Zones to Enhance Safety and Reduce Emissions. Proceedings in the 94th Transportation Research Board Annual Meeting, National Academy of Sciences, Washington DC, 11-15 January 2015, Paper #: 15-0648.
- 21. Li, Q., Qiao, F., Wang, X. and Yu, L. (2013) Impacts of P2V Wireless Communication on Safety and Environment in Work Zones through Driving Simulator Tests. Proceedings of the 26th Annual Conference of the International Chinese Transportation Professionals Association (ICTPA), Tampa, 24-26 May 2013, paper # 26-179.
- 22. Li, Q., Qiao, F., Wang, X. and Yu, L. (2016) Drivers Smart Advisory System Improves Driving Performance at STOP Sign Intersections. Journal of Traffic and Transportation Engineering (English Edition). (in press)
- 23. Li, Q. and Qiao, F. (2014) How Drivers’ Smart Advisory System Improves Driving Performance? A Simulator Imitation of Wireless Warning on Traffic Signal under Sun Glare. LAMBERT Academic Publishing, Saarbrücken.
- 24. Munni, J., Qiao, F., Li, Q. and Yu, L. (2015) Driving Behavior and Emission Analysis at Yellow Interval with Advanced Warning Message under Foggy Weather Condition: A Simulator Test. Proceedings of the 56th Annual Transportation Research Forum in Atlanta, Georgia, 12-14 March 2015, 1-22.
- 25. Li, Q., Qiao, F., Wang, X. and Yu, L. (2015) Driving Performance Test of Stop Signs with Drivers Smart Advisory System. Proceedings of the 28th Annual Conference of the International Chinese Transportation Professionals Association (ICTPA), Los Angeles, 14-16 May 2015, Paper #: 119.
- 26. Qiao, F., Rahman, R., Li, Q. and Yu, L. (2016) Identifying Demographical Effects on Speed Patterns in Work Zones Using Smartphone Based Audio Warning Message System. Journal of Ergonomics. (in press)
- 27. Qiao, F., Li, Q. and Yu, L. (2014) Testing Impacts of Work Zone X2V Communication System on Safety and Air Quality in Driving Simulator. Proceedings of the 21st ITS World Congress, Detroit, 7-11 September 2014, Paper #: T64.
- 28. Li, Q., Qiao, F., Qiao, Y. and Yu, L. (2016) Implications of Smartphone Messages on Driving Performance along Local Streets. Proceedings in the 11th Asia Pacific Transportation Development Conference and 29th ICTPA Annual Conference—Bridging the East and West: Theories and Practices of Transportation in the Asia Pacific, Hsinchu, 27-29 May 2016, Paper #: 81.
- 29. Taehyun, K., Lovell, D.J. and Park, Y. (2003) Limitations of Previous Models on Car-Following Behavior and Research Needs. Proceedings of 82th Transportation Research Board Annual Meeting, Washington DC, 12-16 January 2003, Paper #: 03-3721.
- 30. Chandler, R.E., Herman, R. and Montroll, E.W. (1958) Traffic Dynamics: Studies in Car Following. Operations Research, 6, 165-184.
http://dx.doi.org/10.1287/opre.6.2.165 - 31. Ozaki, H. (1993) Reaction and Anticipation in the Car Following Behaviour. Proceedings of the 13th International Symposium on Traffic and Transportation Theory, Lyon, 24-26 July 1993, 349-366.
- 32. Helly, W. (1959) Simulation of Bottlenecks in Single Lane Traffic Flow. Proceedings of the Symposium on Theory of Traffic Flow, Research Laboratories, General Motors, 207-238.
- 33. Aron, M. (1988) Car Following in an Urban Network: Simulation and Experiments. Proceedings of Seminar D, 16th Planning and Transport, Research and Computation (PTRC) Meeting, University of Bath, England, 12-16 September 1988, 27-39.
- 34. Kometani, E. and Sasaki, T. (1959) Dynamic Behavior of Traffic with a Nonlinear Spacing-Speed Relationship. Proceedings of Symposium on Theory of Traffic Flow, Research Laboratory, General Motors Corp. Elsevier Publishing Co., 105-119.
- 35. Michaels, R.M. (1963) Perceptual Factors in Car Following. Proceedings of the 2nd International Symposium on the Theory of Road Traffic Flow, OECD, Paris, 44-59.
- 36. Fellendorf, M. and Hoyer, R. (1997) Parameterisation of Microscopic Traffic Models through Image Processing. Proceedings of the IFAC Transportation System Conference, Chania, 16-18 June 1997, 929-934.
- 37. Kikuchi, C. and Chakroborty, P. (1992) Car Following Model Based on a Fuzzy Inference System. Transportation Research Record, 1365, 82-91.
- 38. Rekersbrink, A. (1995) Mikroskopische verkehrssimulation mit hilfe der fuzzy-logik. Strass Enverkehrstechnik, 2, 68-74.
- 39. Bando, M., Hasabe, K., Nakayama, A., Shibata, A. and Sugiyama, Y. (1995) Dynamical Model of Traffic Congestion and Numerical Simulation. Physical Review E, 51, 1035-1042.
http://dx.doi.org/10.1103/PhysRevE.51.1035 - 40. Treiber, M., Hennecke, A. and Helbing, D. (2000) Congested Traffic States in Empirical Observations and Microscopic Simulations. Physical Review E, 62, 1805-1824.
http://dx.doi.org/10.1103/PhysRevE.62.1805 - 41. Nagel, K. and Schreckenberg, M. (1992) A Cellular Automaton Model for Freeway Traffic. Journal de Physique, 2, 2221-2229.
http://dx.doi.org/10.1051/jp1:1992277 - 42. Fukui, M. and Ishibashi, Y. (1996) Traffic Flow in 1D Cellular Automaton Model Including Cars Moving with High Speed. Journal of the Physical Society of Japan, 65, 1868-1870.
http://dx.doi.org/10.1143/JPSJ.65.1868 - 43. Hanken, A. and Rockwell, T.H. (1967) A Model of Car Following Derived Empirically by Piece-Wise Regression Analysis. Proceedings of the 3rd International Symposium on the Theory of Traffic Flow, New York, June 1967, 40- 41.