Journal of Transportation Technologies
Vol.4 No.2(2014), Article ID:45044,9 pages DOI:10.4236/jtts.2014.42014
Calibration and Evaluation of Link Congestion Functions: Applying Intrinsic Sensitivity of Link Speed as a Practical Consideration to Heterogeneous Facility Types within Urban Network
Enock T. Mtoi*, Ren Moses
Civil and Environmental Engineering, FAMU-FSU College of Engineering, Florida State University, Tallahassee, USA
Email: *et09j@my.fsu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 January 2014; revised 23 February 2014; accepted 21 March 2014
Abstract
This paper explores the use of archived data to calibrate volume delay functions (VDFs) and updates their input parameters (capacity and free-flow speed) for planning applications. The sensitivity analysis of speed to change in congestion level is performed to capture functional characteristics of VDFs in modeling specific facility types. Different sensitivity characteristics shown by the VDFs indicate that each function is suitable to a particular facility type. The results of sensitivity analysis are confirmed by the root mean square percent error (RMSPE) values calculated using the Orlando Urban Area Transportation Study (OUATS) model results and observed data. The modified Davidson’s function exhibits remarkable performance in nearly all facility types. The strength of the modified Davidson’s function across a broad range of facilities can be attributed to the flexibility of its tuning parameter, μ. Fitted Bureau of Public Road (BPR) and conical delay functions show lower RMSPE for uninterrupted flow facilities (freeways/expressways, managed lanes) and higher values for toll roads (which might have partial interruptions due to toll booths) and signalized arterials. Akcelik function underperforms on freeways/expressways and managed lanes but shows some improvements for toll roads and superior results for the signalized arterials. This was a desired strength of Akcelik function when modeling link travel speed on facilities where stopped delays were encountered.
Keywords
Travel Demand Modeling, Congestion Functions, ITS Data Applications

1. Introduction
In the state-of-the-practice traffic assignment methods, the highway capacity constraints on travel speeds or travel times are specified by means of volume-delay functions (VDFs) or link congestion functions (LCFs). These functions express the travel time (or travel cost) on a highway link as a function of traffic volume. Congestion function can be represented in terms of speed on a link, as u = f(θ,v) where u is the estimated speed on the link carrying traffic volume, v and θ represent a vector of parameters describing link characteristics. The function starts with a finite travel speed, u0, at free flow, and then the actual travel speed decreases with increasing volume. The rate of decrease is small for low volumes, but accelerates once volumes build up towards the capacity of the link.
Typically, most highway links in the travel demand models derive free-flow speeds and link capacities via a look-up table that relates these variables to the facility type or functional class of the link and the area type surrounding the link. These input parameters from look-up tables need to be updated regularly to ensure that modeled outputs on highway networks closely reflect actual observations from count stations such as loop detectors. Accurate volume, occupancy, speed and other necessary traffic data are crucial for robust model development and hence reliable calculation of vehicle hours traveled (VHT), time-of-day traffic assignments, development of Congestion Management Plans (CMPs), highway and transit corridor analyses, and air quality emissions analysis. In order to implement the previously mentioned calculations, travel speeds, which are routinely obtained from travel demand models at link level, are used. However, the conventional travel demand forecasting procedures do not typically generate sufficiently accurate speed estimates [1] . Recent and ongoing advances in traffic modeling are expected to produce more realistic estimation of speed but majority of the proposed techniques (e.g. simulations) are difficult to use for regional scale modeling due to significant amount of data requirements and high computational overhead [2] . Two out of many published research studies [3] [4] proposed speed postprocessing as a cost-efficient alternative to simulation. Although most post-processing approaches are reported to produce speeds comparable to those derived from operational or simulation models, there has been little research exploring comparatively lower cost approaches of using extensive data currently being collected by public and private sector to update the look-up tables and calibrate the VDFs for reliable model outputs.
The objective of our research is to calibrate speed models and update their input parameters for Florida highways. The research is consistent with the consensus of the Florida Standard Urban Transportation Model Structure (FSUTMS) Task Force, which found that speed models and data used for traffic projection and model validation in Florida need to be enhanced. The main sources of data used in this study were Telemetered Traffic Monitoring Sites (TTMS) operated by Florida DOT Statistics Office and the Statewide Transportation Engineering Warehouse for Archived Regional Data (STEWARD) database. We evaluated the most commonly used classical VDFs and calibrate them using the field data. The VDFs covered in this paper are Bureau of Public Roads (BPR) curve, Davidson’s delay model, Akcelik function and conical delay model. These functions are shown in Table 1. Their derivatives are the measure of speed sensitivity to change in congestion level or demand.
The notations used for each function are: u, the speed as a function of link volume v; u0, the free-flow speed; c, the capacity; x, degree of saturation or volume to capacity ratio (v/c); t, the travel time per unit distance corresponding to link volume v; t0, the travel time under free flow conditions; and T, which designates the analysis period. Here α, β, μ, J, and τ are the parameters to be calibrated. The following sections describe the main characteristics of each VDF in Table 1.
1.1. Standard and Modified BPR Functions
The standard BPR curve was derived in the late 1960s by BPR (now the Federal Highway Administration, FHWA) by fitting a polynomial equation to the freeway speed-flow curves in the 1965 HCM [5] . Efforts have been made by various metropolitan planning organizations (MPOs) to advance and modernize the original for
Table 1. Evaluated volume delay functions and their derivatives..
mulation of the BPR curve by fitting local data or hypothetical data from simulation models. This resulted in different forms of the BPR curve throughout the United States and the world at large. This function presumes that coefficient α (often set to 0.15) is the ratio of travel time per unit distance at practical capacity to that at free flow, and parameter β (often set to 4) determines how fast the estimated average link speed, u as a function of x, decreases from free-flow to congested conditions. With higher values of β, the onset of congestion effects becomes more and more sudden [6] .
Minimal input requirements and simple mathematical form are the two main attributes that have contributed to the widespread use of the BPR function. In addition, it is also easy to develop efficient algorithms for finding the equilibrium solution by differentiating the BPR function [7] . However, the standard BPR curve has a number of limitations. Its derivation was based on data that do not reflect current operating conditions and does not take into account facility characteristics, such as signalization conditions on arterials [7] . These drawbacks led several planning organizations to propose modified BPR curves to match local travel activities [3] [4] [7] [8] .
1.2. Davidson’s Delay Model
The original Davidson function had a simpler form, given only by part (i) of that in Table 1. The Davidson function became popular in economic analysis and travel demand modeling for road networks, largely on account of its flexibility and ability to carter for a wide range of traffic conditions and environments [9] . However, the original Davidson function had one serious flaw. It could not define travel time for link volumes exceeding the capacity. This could provide computational problems in network loading model, which determines link volumes iteratively, and as a result, might occasionally overload some links in computing its intermediate solutions [9]. A modification involving the addition of a linear extension term as a second component (ii) to the function was proposed and used in transportation planning practice [10] . The modified Davidson function is shown in Table 1. The parameter μ is a user-selected proportion, usually in the range (0.85, 0.95), which provides a finite definition of the function for all finite x [9] . It also allows for link oversaturation. J is the parameter associated with land use or area type surrounding the highway link.
1.3. Akcelik Delay Function
Akcelik [11] proposed a time-dependent form of the Davidson function using the coordinate transformation technique, which attempted to encompass the intersection delay. This delay function improved modeling of link travel speed when significant portion of it is provided by intersection delays. The delay is captured by a parameter τ. Lower values of τ are suggested for freeways/coordinated signal systems while higher values are used for arterial roads without signal coordination [11] . Akcelik function has been tested for planning applications and observed to often provide the best fit when comparing various speed delay functions to data collected from 119 freeway segments located in California [7] . Singh [12] also indicated that the use of Akcelik function in traffic assignment had some other advantages, such as better convergence and more realistic speed estimation under congested conditions. Akcelik function is also useful because of its conciseness: a uniform functional form can be used everywhere and the complex parameters in computing intersection delay are avoided.
1.4. Conical Delay Model
Spiess [6] proposed the conical link-congestion function to overcome the drawbacks associated with high exponent β values of the BPR function. Spiess [6] found that high values of β can reduce the rate of convergence by giving undue penalties to overloaded links during the first few iterations of an equilibrium assignment and can also cause numerical problems, such as overflow conditions and loss of precision. Additionally, for links with volumes that are far below capacity, the BPR function with high β values always yields free-flow speeds that do not match those of the actual traffic volumes. The conical link-congestion function proposed by Spiess [6] is shown in Table 1. The use of this function resulted in a remarkable improvement in the convergence of equilibrium assignment when it was used in a transportation study for the City of Basel, Switzerland [6] .
2. Research Motivation
The process of refining the outputs of regional travel demand models depends on data that reflects regional travel activities. Travel demand models comprise complex computation steps nested together to accomplish multifaceted travel behavior in the network. Each step is represented by mathematical model, which needs to be calibrated, validated, and updated regularly to cope with the changes in trends of travel demand and behavior. The common practice is to calibrate and validate each step individually and not the entire model at once. This is done in order to control and minimize propagation of errors from one step to other subsequent steps. For instance, in the four-step travel demand model, the estimation, calibration, validation, and updating of the first three steps (i.e. trip generation, distribution, and mode choice) count on census and survey data collected locally. The level of complexity differs from each step. With the fourth step, highway assignment, it has been difficult to use locally collected data from traffic counts due to limited resources to make the data usable for modeling. This study is motivated by the need to provide a direct approach to fit and calibrate VDFs, and conduct sensitivity analysis as an additional criterion in the selection of an appropriate VDF for a particular facility type. The data used in this approach was acquired from TTMS and STEWARD. This extensive data coverage in Florida highways captures all important traffic variability necessary for accurate modeling.
3. Calibration of Volume-Delay Functions
3.1. Free-Flow Speed and Capacity Estimation
This study was accomplished using detector data collected for a one-year period beginning July 1, 2010 and ending June 30, 2011. Data from 262 monitoring stations, known as Telemetered Traffic Monitoring Sites (TTMS), were acquired from Statistics Office of the Florida Department of Transportation. Additional data from statewide transportation engineering warehouse for archived regional data (STEWARD) was also used. STEWARD database contains daily summaries of traffic volumes, speeds, occupancies and travel times obtained from SunGuide® transportation management centers (TMCs) in Florida [13] .
From TTMS and STEWARD data, free-flow speeds ( Table 2) were estimated based on average speeds of vehicles under low flow conditions of density less than 10 passenger cars per hour per mile per lane (pc/h/ln) for uninterrupted flow facilities. In interrupted flow facilities, a vehicle is considered to be free flowing when it has headway of 8 seconds or more to the vehicle ahead and 5 seconds or more to the vehicle behind in the same lane [14] . Therefore, the free-flow speed in interrupted flow facilities was calculated as the average of speeds of all vehicles fulfilling the conditions stated in the previous statement. In both facilities, the practical capacity was estimated as the 99th percentile flow in pc/h/ln as opposed to maximum hourly flow (qmax) in order to exclude outliers.
Table 2 . Field estimated free-flow speeds and capacities.
3.2. Calibration and Sensitivity Analysis of VDFs
Estimation of model parameters for four most commonly used volume-delay functions (VDFs) was conducted using curve fitting tools in MATLAB.
The estimation was conducted for four facility types namely freeways or expressways, toll roads, managed lanes (HOV or HOT lanes), and signalized facilities as shown in Table 3. Each category of facility type comprises of three area types distinguished by land uses: urban (1), residential (2) and rural (3).
The models fitted were BPR function, conical delay function, modified Davidson’s function, and Akcelik function. The models were then plotted against observed field data for visual analysis as shown in Figure 1 below. This figure shows results of a typical urban freeway segment located in Pompano Beach, Florida on Interstate 95 (I-95).
The results in Figure 1 show that modified or fitted BPR fits the data well, followed by modified Davidson, conical delay function, and lastly Akcelik function. However, these results are not the final judgment to which VDF performs better compared to others. This is due to the fact that, in a congested network, a VDF will perform differently given different facility types. For that reason, the selection of VDF for a particular facility type and area type needs sturdy knowledge of transportation network behavior under different congestion levels and different traffic controls. It is obvious that, the effect of change in congestion, near or at capacity, will have different impact on travel speed for a freeway link compared to a signalized arterial link. Speed tends to deteriorate faster in shorter links (urban signalized arterials) than in longer links (uninterrupted flow facilities such as freeways and expressways) when demand is close to capacity. Therefore, the selection of a VDF for a particular facility type should not only rely on statistical performance measures such as root mean square error (RMSE) or coefficient of determination (R2) but also account for sensitivity of link travel speed to change in congestion or demand, which is measured as a slope of a VDF at a given congestion level which, in this paper, is measured as volume to capacity ratio, x.
Figure 2 shows the behavior of each fitted VDF as demand level, x, changes. When demand is lower than capacity (up to x = 0.7), the slopes of the VDFs remain fairly unchanged (du/dx ≈ 0), meaning that the users in the link are free-flowing. The slopes become steeper when demand approaches capacity. Conical, Akcelik and modified Davidson reach their steepest slopes at capacity (x = 1.0) different from fitted BPR which reaches its steepest slope at a demand 20% higher than capacity (x = 1.2). At higher demands (x![]() 1) when the link is al
1) when the link is al
Table 3 . Parameter estimates for fitted models.
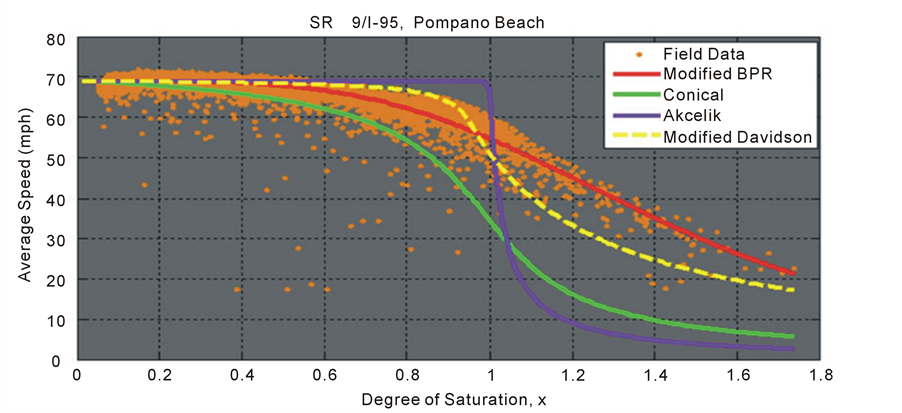
Figure 1. Speed variation as a function demand to capacity ratio.

Figure 2 Sensitivity of link travel speed to change in demand.
ready congested the slopes change from steep to gentle (du/dx ≈ 0 at higher values of x).
With respect to network performance, we can interpret the results in Figure 2 as follows: a link is robust to change in demand if either the demand or travel speed is low—that is, changes in demand have lesser effect to travel speed if there are a few travelers in the link (free-flow condition), or if the link is already highly congested, and therefore the speed will not deteriorate much further.
Different sensitivity characteristics shown by the VDFs (Figure 2) indicate the suitability of each function to a particular facility type. The stability manifested by the fitted BPR, is consistent with the behavior of long stretches of uninterrupted flow facilities, such as basic freeway segments with low ramp density. Modified Davidson matches facilities with medium access density such as freeways and expressways in fringe or outlying business district (OBD), segments of toll roads with medium spaced toll plazas, or multilane highways with highly isolated signals. Speed modeling in freeways with high ramp density, toll roads with closely spaced toll booths or plazas, or multilane highways with medium spaced signals, can be achieved by using conical delay function. The behavior depicted by Akcelik function, is a characteristic of urban streets with closely spaced signalized intersections.
4. Testing the Calibrated Volume Delay Functions
The Orlando Urban Area Transportation Study (OUATS) Model was selected as the travel forecasting model for testing the volume delay functions and their calibrated parameters. The OUATS model is a daily travel forecasting model with a region covering five counties in central Florida. The counties covered by OUATS model are Volusia (West), Lake, Seminole, Orange, Polk (Northeast), and Osceola. This regional model was chosen due to its capability to analyze time of day traffic. In addition, this is one of the most congested regions in Florida and comprises a broad diversity of facility types, ideal for testing the performance of calibrated VDFs.
The calibrated functions and their input parameters were coded into OUATS travel forecasting model running on CUBE Voyager platform. The 2010 model scenario of was run to forecast the typical weekday 24-hour highway assignments for each of the four VDFs being tested. The model results for the 7:00-8:00 a.m., 8:00-9:00 a.m., 5:00-6:00 p.m. and 6:00-7:00 p.m. hours were analyzed and compared to actual data obtained from count stations (TTMS) within the model region. The comparison was made in terms of observed volumes from the count stations against forecasted volumes from model output, and root mean square percent error (RMSPE) was used as the measure of model accuracy.
This analysis was disaggregated by facility types in order to capture the assignment performance of each function for a particular type of facility.
The results in Figure 3 are relatively consistent with the results of sensitivity analysis from Figure 2. As the results of sensitivity analysis suggested, the modified Davidson’s function, showed impressive performance in almost every facility type. The strength of the modified Davidson’s function across a broad range of facilities could be attributed by the flexibility of its parameter μ, which can be tuned to reflect any level of congestion and link type in the network. Other functions performed differently in different facility types. Fitted BPR and conical functions showed lower RMSPE in uninterrupted flow facilities (freeways/expressways, HOV/HOT lanes) and higher values in toll roads (which might have partial interruptions due to toll booths) and signalized arterials. Akcelik function underperformed in freeways/expressways and HOV/HOT lanes but showed some improvements in toll roads and superior results for signalized arterials. This is a desired strength of Akcelik function when it comes to modeling link travel speed in facilities where stopped delays are encountered.
5. Conclusions and Future Research
This paper explored the use of archived public data to calibrate VDFs and update their input parameters (capacity and free-flow speed) for planning applications. The study was accomplished using TTMS data and daily summaries of traffic volumes, speeds, occupancies and travel times obtained from STEWARD database. The behavior of each calibrated curve was studied by conducting sensitivity analysis. The stability manifested by the fitted BPR, was consistent with the behavior of long stretches of uninterrupted flow facilities with low ramp densities. Facilities in fringe or outlying business district (OBD) areas, toll roads with medium spaced toll booths or plazas, or multilane highways with highly isolated signals could be characterized by modified Davidson’s function. Speed modeling in freeways with high ramp density, toll roads with closely spaced toll plazas, or multilane highways with medium spaced signals, could be described by conical delay function. The behavior depicted by Akcelik function, was a characteristic of urban streets with closely spaced signalized intersections.
The results of sensitivity analysis were further confirmed by the RMSPE values calculated from OUATS model results and observed data. Modified Davidson’s function exhibited remarkable performance in nearly all facility types. The strength of the modified Davidson’s function across a broad range of facilities could be attri-

Figure 3. Root mean square percent errors from comparison of forecasted to observed traffic.
buted by the flexibility of its tuning parameter μ. Fitted BPR and conical delay functions showed lower RMSPE in uninterrupted flow facilities (freeways/expressways, HOV/HOT lanes) and higher values in toll roads (which might have partial interruptions due to toll booths) and signalized arterials. Akcelik function underperformed in freeways/expressways and HOV/HOT lanes but showed some improvements in toll roads and superior results for signalized arterials. This was a desired strength of Akcelik function when modeling the link travel speed in facilities where stopped delays were encountered.
Future directions of this research are focused on developing the dynamic area types, which will be determined as a function of activity density. This will enable the model to dynamically determine the area type and replace the existing hard-coding methodology. We will also invest efforts in exploring the applicability of TTMS and STEWARD data in calibration and validation of dynamic traffic assignment models and activity based models.
References
- Stopher, P.R. and Fu, H.Q. (1998) Feasible Improvements to Travel-forecasting Procedure for Air Quality Analysis. Transportation Planning and Air Quality III: Emerging Strategies and Working Solutions. American Society of Civil Engineers, Washington DC
- Bai, S., Nie, Y. and Niemeier, D.A. (2007) The Impact of Speed Post Processing Methods on Regional Mobile Emissions. Estimation Transportation Research Part D: Transport and Environment, 12, 307-324.
- Dowling, R. and Skabardonis, A. (1993) Improving the Average Travel Speeds Estimated by Planning Models. Transportation Research Record, 1360, 68-74.
- Helali, K. and Hutchinson, B. (1994) Improving Road Link Speed Estimates for Air Quality Models. Transportation Research Record, 1444, 71-77.
- Transportation Research Board (1985) Special Report 209: Highway Capacity Manual. National Research Council, Washington DC
- Spiess, H. (1990) Conical Volume-Delay Functions. Transportation Science, 24, 153-158. http://dx.doi.org/10.1287/trsc.24.2.153
- Skabardonis, A. and Dowling, R. (1997) Improved Speed-Flow Relationships for Planning Applications. Transportation Research Record, 1572, 18-23. http://dx.doi.org/10.3141/1572-03
- Data Management Group (1991) Road Network Coding Manual. Joint Program in Transportation, University of Toronto, Toronto.
- Taylor, M.A.P. (1997) The Effects of Lower Urban Speed Limits on Mobility, Accessibility, Energy and the Environment: Trade-Offs with Increased Safety? Final Report for the Federal Office of Road Safety, Canberra.
- Tisato, P. (1991) Suggestions for an Improved Davidson Travel Time Function. Australian Road Research, 21, 85-100.
- Akcelik, R. (1991) Travel Time Functions for Transport Planning Purposes: Davidson’s Function, Its Time Dependent Form and an Alternative Travel Time Function. Australian Road Research, 21, 49-59.
- Singh, R. (1999) Improved Speed-Flow Relationships: Application to Transportation Planning Models. Proceedings of 7th TRB Conference Application of Transportation Planning Methods, Boston, 7-11 March 1999, 340-349.
- Statewide Transportation Engineering Warehouse for Archived Regional Data (Accessed May 2012) (STEWARD). http://cce-trc-cdwserv.ce.ufl.edu/steward/
NOTES

*Corresponding author.


