Journal of Signal and Information Processing
Vol.06 No.03(2015), Article ID:57957,11 pages
10.4236/jsip.2015.63018
Census and Segmentation-Based Disparity Estimation Algorithm Using Region Merging
Viral H. Borisagar1, Mukesh A. Zaveri2
1Computer Engineering Department, Government Engineering College, Gandhinagar, India
2Computer Engineering Department, Sardar Vallabhbhai National Institute of Technology, Surat, India
Email: viralborisagar@gmail.com, mazaveri@coed.svnit.ac.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2015; accepted 11 July 2015; published 15 July 2015
ABSTRACT
Disparity estimation is an ill-posed problem in computer vision. It is explored comprehensively due to its usefulness in many areas like 3D scene reconstruction, robot navigation, parts inspection, virtual reality and image-based rendering. In this paper, we propose a hybrid disparity generation algorithm which uses census based and segmentation based approaches. Census transform does not give good results in textureless areas, but is suitable for highly textured regions. While segment based stereo matching techniques gives good result in textureless regions. Coarse disparities obtained from census transform are combined with the region information extracted by mean shift segmentation method, so that a region matching can be applied by using affine transformation. Affine transformation is used to remove noise from each segment. Mean shift segmentation technique creates more than one segment of same object resulting into non-smooth- ness disparity. Region merging is applied to obtain refined smooth disparity map. Finally, multilateral filtering is applied on the disparity map estimated to preserve the information and to smooth the disparity map. The proposed algorithm generates good results compared to the classic census transform. Our proposed algorithm solves standard problems like occlusions, repetitive patterns, textureless regions, perspective distortion, specular reflection and noise. Experiments are performed on middlebury stereo test bed and the results demonstrate that the proposed algorithm achieves high accuracy, efficiency and robustness.
Keywords:
Stereo Vision, Census Transform, Mean Shift Segmentation, Affine Transform, Region Merging

1. Introduction
Stereo vision is a fundamental problem in computer vision. An extensive analysis of stereo matching algorithms can be found in [1] . Stereo vision can be divided into two problems: matching and 3D reconstruction. Out of these two, matching is considered to be the significant and complex problem. Matching is done to find corresponding points between stereo image pairs. Two image points Pl in left image and Pr in right image match if they result from the projection of the same point P in the scene, for example, Pl and Pr will have similar intensity or color. The difference in the location of the two corresponding points in their respective images is called disparity. The appearance of corresponding points will vary in stereo images due to different perspective projections. For a point in one image, there are many possible corresponding points in the second image, especially in repetitive texture or textureless regions. This is called problem of ambiguity. Disparity depends on both, the position of the point in the scene and the position, orientation and physical characteristics of the stereo cameras.
Matching technique may be usually classified on the basis of the type of matching primitives used [2] . Area based algorithms [1] [3] are typically based on correlation. These algorithms are easy to implement. These methods calculate the disparity of a pixel by using the intensity values within a fixed corresponding neighboring window in another image. A small window will generate various non continuous structures, while a large window will lead to too smooth disparity map. These algorithms are very susceptible to variation of contrast, absolute intensity, and illumination which decreases the reliability of disparity estimation and cannot be easily integrated with global consistency criterion. These algorithms make smoothness assumption at the cost aggregation step i.e., all pixels in a support window have identical disparities. These algorithms generate dense but unreliable disparity maps. These methods give high-quality results in textured regions and fail at occluded areas, textureless regions and edges.
In feature-based approaches [3] , features such as texture, edge and corner are used as the matching primitives. These methods depend on feature extraction. As the features are sparse and unevenly dispersed, these methods produce a sparse disparity map. So it is hard to ensure its accuracy and precision. Disparity map estimated by these techniques are reliable because the features are more stable to photometric variations. These algorithms are speedy. These methods perform more accurate matching than area based matching techniques. The accuracy mostly depends on the number of reliable features identified. It is difficult to match distinct features due to outliers.
In transform-based approaches, transformation of the pixel values in the stereo images is carried out before matching. The transformed images may then be matched using area-based metrics. Non-parametric transforms including the rank and census transforms [4] are the examples of transform-based approaches.
There are various issues [5] that make stereo complex problem. The issues are either scene-related or camera- related. Occlusions, textureless regions, non-Lambertian surfaces, reflections and translucency are the issues related to the property of the scene itself. Image noise and errors due to imperfect calibration are the camera-re- lated issues. The utilization of many cameras introduces another set of problems like white balancing, variation in exposure and other radiometric properties.
Zabih and Woodfill [4] introduced census transform as a nonparametric local transform to be used as the basis for correlation. Census transform is extensively used in many computer vision applications. It provides high resistance to radiometric distortion, vignette, and noise because it is based on the relative ordering of local pixel intensity values [4] . It has various advantages like illumination invariance, compared to other matching techniques like Sum of Squared Differences (SSD) or Sum of Absolute Differences (SAD).
Census transform may create noise in the uniform regions while being able to maintain good result in regions having variable disparity. This is because in uniform regions the most of the pixels fit in to the same object. The intensities of the pixels in such regions are all identical to each other; hence only by using magnitude relationship it’s tough to calculate the best disparity value. On the other hand, in regions having variable disparity different objects with relevant disparities will all be included in the census transform window which can offer a large amount of information to centre pixel by magnitude difference. This clear difference in performance of census transform in texture and textureless regions is the motivation for our proposed approach. As adjacent pixels with similar colors have similar or continuous disparity, image segmentation is utilized to simplify the stereo problem [5] . This has three significant advantages. Firstly, it lessens the uncertainty related to textureless areas. Due to image segmentation depth discontinuities takes place at color boundaries. Secondly, larger segments will decrease the computational complexity. Finally, noise tolerance is improved by aggregating over similar colored pixels. Human recognize the objects by analyzing features such as color, texture and shape of the objects. Area-based methods alone are inefficient in textureless regions, occluded areas and edges. Thus segment based stereo matching algorithm is used in our proposed approach along with census transform.
The rest of the paper is organized as follows: In Section 2, related work is explained in detail. Section 3 presents proposed algorithm. Section 4 shows experimental results with its discussions and demonstrates the performance of our algorithm. Section 5 draws the conclusion and future work of this paper. Finally, Section 6 lists out bibliography.
2. Related Work
A large number of algorithms for disparity map generation are pixel based in which the disparity is calculated pixel-by-pixel. Pixel based methods does not give good results in textureless surfaces. Noise is typically present in disparity calculated for such surfaces. Compared to the large number of research papers on pixel-based disparity map generation algorithms, there are not many related to region-based disparity estimation algorithms [6] [7] .
The study of different similarity measures is performed in [8] . Area-based stereo matching algorithms are used in most of the real-time stereo vision applications. Sum of absolute difference (SAD), sum of squared difference (SSD) and normalized cross correlation (NCC) are frequently used similarity measures. Area based disparity estimation algorithms does not make the use of the information associated with the shape of the objects in the images. They also perform worse on areas like edges. Segmentation based methods can perform better, as they assume that the disparity discontinuities coincides with object’s depth discontinuities (segment’s edges). So it is more robust on edges and other depth discontinuous regions.
While most of the pixel based methods are susceptible to variation in camera gain or bias, non-parametric methods such as rank and census transforms [4] and gradient-based methods [9] [10] are not. Nonparametric matching costs are robust against outliers that occur in area based methods near edges [4] [11] . Compared to area based methods, census based stereo matching methods performs with high efficiency and is suitable for the real-time applications. Census based techniques have exceptional ability of signal conversion, and it gives quality results. It is based on local intensity relations between the actual pixel and the pixels within a certain window. The relative ordering of intensity values rather than the intensity values themselves offers robustness against radiometric distortion and vignette [8] . Census transform can significantly enhance the matching performance of images in the nonideal condition. The variation in bias and gain between two images will not alter the sequence of pixels within a window. It improves the matching cost to additive or multiplicative intensity variations caused by different shutter times and illumination conditions of the cameras. Non-parametric transforms works well in image regions having same colours and commonly used area based similarity measures like SAD and SSD gives good results for image regions with same local structures [12] . The assessment of similarity measures [11] shows that census transform gives quality results in the presence of simulated and real radiometric differences except in the presence of strong image noise.
Census [4] cost function is found to be very robust against illumination variations from the assessment of cost functions in [8] [11] . False matching is done when the centre pixel is modified by the illumination variation between two cameras and by the bias. The values of the census transform are very sensitive to high-frequency noise because these are dependent on the value of the centrepixel [13] . For census transform calculations, the average of the intensity values in the window is used in [13] instead of centre pixel value. The neighborhood pixels are probably affected and may have slight deviation in non ideal conditions like illumination variation. The performance of census transform is better than other LOG filter-based speedy approaches [13] -[15] .
In census transform, if fewer pixels in a local neighborhood have a very diverse intensity distribution compared to majority pixels, only comparisons relating that fewer pixels are affected. The variable size increases as the dimensions of the window increases. The variable used to store the census value would be of size 23 or 8 bits for a census window of 3 × 3. While for a census of window size 5 × 5, 25 or 32 bits are required to store census value.
Figure 1 shows an example of the census transform of image with respect to the centre pixel of the window. Census transform translates relative intensity variation to 1 or 0 in one dimensional vector structure.
Thus using census transform every pixel within an image is transformed into a sequence of bit representing the intensity relations between the centre and its neighboring pixels. Census transform is invariant to changes in gain and bias. As shown in Figure 2, vector is assigned to a pixel and an image is transformed into 3 dimensional data.
In [16] segmentation of either the left color image or the computed texture image is done for the improvement
Figure 1. Census transform example.
Figure 2. Disparity space image (DSI) defined by the dimensions of the left image and the disparity search range.
of the matching quality at textureless regions and occlusions. Census based correlation method is used to calculate the local cost. The confidence of a match is calculated and by computing a disparity plane for the corresponding segment, non-confident or non-textured pixels are estimated. Modified Semi-Global Matching (SGM) step with sub pixel accuracy is utilized to enhance the quality of the local optimized matches. Instead of whole image, horizontal stripes of the image are used for disparity optimization.
Various well performed stereo matching algorithms are often complex and have high computational complexity. In [17] , the disparity is estimated by using the census diffusion with segment constraint. Compared to adaptive support weight, the complexity of the algorithm is same, but the runtime is much shorter than that of the adaptive support weight and other global methods excluding Bayesian diffusion. The qualitatively and quantitatively performance of this algorithm is somewhat worse than the state-of-the-art complex algorithms, but this method is having comparatively lesser complexity and run time.
Segment-based methods [18] -[21] have become popular because of their excellent performance on managing boundaries, textureless areas and improving noise tolerance. Stereo matching becomes easier even in the presence of outliers, intensity variation and minor deviation in segmented region. They are based on the hypothesis that the scene structure can be estimated by a set of non overlapping planes in the disparity space and that each plane of target image is coincident with at least one uniform color segment in the reference image. Larger segments lead to much reduced computational complexity. Instead of allocating accurate disparity cost to each pixel one by one in the local matching methods, segmentation based algorithms assigns a disparity plane to one uniform color segment in the image. Thus the robustness of algorithms is enhanced against outliers or noise in the image.
Small segments may be inefficient for estimating surfaces like slanted plane, while segmentation errors in large segments can affect the efficiency of disparity cost estimation. Similar colors in image do not always represent similar disparity value. For example, the projected image region of an extremely slanted Lambertian plane having uniform texture tends to be categorized as one image segment having similar disparity. Image can be segmented by a large number of segmentation methods available and after segmentation step further pro- cessing is carried out on this segmented image. Few segmentation based stereo matching algorithms do not take into consideration the quality of segments, which results into incorrect disparity computation.
Segment based stereo matching algorithms usually consists of four successive steps. First step is to segment the reference image using proper segmentation technique; second step is to generate initial disparity map using local matching technique; in third step, a plane fitting method is utilized to obtain disparity planes; lastly, an optimal disparity map is estimated using optimization technique like BP or graph cut.
A hybrid disparity map generation method which combines the pixel-based and region-based approaches is proposed in [22] . Initially a pixel-based approach based on the gabor transform and variational regularization is carried out and then the region information from the mean shift segmentation is combined with the pixel-based disparity results and latter a region matching scheme using affine transform can be applied. This method is used to evaluate the change of disparity histograms after region matching to identify the occluded areas and to estimate the true disparity values for such regions. This hybrid algorithm produces quality disparity maps and solves few standard problems associated with disparity map generation.
Mean shift segmentation technique [23] has been used in [6] to segment the images into different areas. Over- segmentation is applied to each area rather than direct region matching in the next step. It can be assumed that every area in one image of the stereo pair is an affine transform of the same area in another image. Thus region based disparity generation is transformed into the evaluation of affine parameters for each area.
Color mean-shift segmentation on the reference image is carried out and thereafter local matching based on windows is utilized in [24] . In [25] a region based cooperative optimization stereo matching algorithm has been proposed. From its initial disparity generation, this algorithm gives quality disparity map results. As regions contain more information compared to individual pixels, a novel region based progressive stereo matching algorithm is presented in [6] . This method assumes that pixels within the same area have the similar disparity values.
A novel stereo matching algorithm is presented in [21] in which color segmentation on the reference image is carried out and a self adapting matching score increases the number of accurate correspondences. The scene structure is modeled by a set of planar surface patches which are estimated using a new method that is more robust to outliers. Disparity value is not assigned to each pixel but a disparity plane is assigned to each segment. The optimal disparity plane labeling is carried out by applying belief propagation.
3. Proposed Algorithm
A novel census and segmentation based disparity estimation algorithm using region merging is proposed which gives quality disparity map as output from input stereo image pair. Census transform produces quality results in depth discontinuous regions but may generate noise in textureless regions. Region matching technique is used to solve this issue. Our algorithm solves issues like occluded regions and keeping edges sharp and clear while preserving the smoothness of surfaces. These problems cannot be solved by census and segmentation based technique separately. The proposed algorithm produces quality results compared to the classic census transform.
The rectified stereo image pair is given as input to the proposed algorithm. In the rectified images the pixel rows are aligned in parallel to the baseline which makes matching efficient. Rectified images satisfy the epipolar constraint, which can lessen the search along one corresponding row. Bilateral filter [26] is applied to both left and right images as a preprocessing step. A bilateral filter is used to preserve edge and to decrease noise. A weighted average of intensity values from neighborhood pixels is used to change the intensity value at each pixel in an image. This weight is based on a Gaussian distribution. The weights depend on Euclidean distance as well as on the radiometric differences. This conserves sharp boundaries by methodically looping through each pixel and calculating weights to the nearby pixels accordingly.
Stereo image pairs are generally acquired by different cameras sometimes at different time. Typically the brightness is inconsistent in corresponding areas of stereo image pair. This increases complexity for stereo matching techniques assuming brightness consistency between two images. Census transform makes use of relative intensity of input images leading to robustness under different absolute intensities of input images and noises. Census transform is applied on both filtered images for disparity estimation. Census transform can be divided into two steps: transform step and correlation step. Calculation of a bit string, which summarizes local texture of the current corresponding pixel pair from left and right window centre is done in transform step. Comparison of two strings using the hamming distance, i.e. count of differing bits is accomplished in correlation step. Finally, disparity is selected by referring to the best window pair containing the minimum hamming distance. Below are the details of both steps:
The census transform is realized with a comparison function ξ (Equation (1)) which converts the intensity values into 1 or 0. This function compares the intensity value of the centre pixel 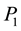 with the other pixels
with the other pixels  in the neighbourhood.
in the neighbourhood.
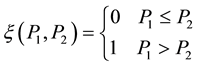 (1)
(1)
where, 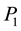 is the centre pixel and
is the centre pixel and 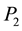 is the neighborhood pixels within the image. It produces 1 if the centre pixel is larger, otherwise 0. The result then is concatenated (
is the neighborhood pixels within the image. It produces 1 if the centre pixel is larger, otherwise 0. The result then is concatenated (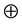 ) to a bit-vector.
) to a bit-vector.
Matching is the next step after census transform. The cost for possible match has to be calculated for each pixel. The hamming distance is computed between census-transformed pixels by performing XOR operation between two binary strings and counting the number of set bits in the output string for finding the matching value for each pixel. The costs are computed using Equation (2) and is stored in three-dimensional data structure Disparity space image (DSI) [27] , with size disparity ×width × height as shown in Figure 2. Census transform creates data of (image size × vector size).
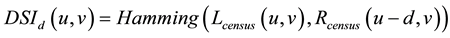 (2)
(2)
where the left image is the reference image and the right image shifts horizontally from right to left.
The hamming distance is minimized after applying the census transform to calculate the matching value. For a pixel  in left image, the matching cost is calculated for pixels
in left image, the matching cost is calculated for pixels ,
, 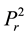 , .…,
, .…,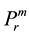 in right image using Equation (3).
in right image using Equation (3).
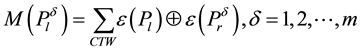 (3)
(3)
where ∑ is the hamming distance between two bit strings 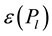 and
and ,
, 




Thus, disparity map between left and right image is computed by using Equations (2) and (3). The output disparity is having integer value but generally the true disparity lies somewhere in between two pixels. Due to this the minimum disparity value plus both adjacent disparities are taken into consideration and sub pixel accuracy is applied. The sub-pixel refinement adds additional accuracy to the disparity map output.
Median filter is applied on disparity map obtained to remove some outliers. This filter is popular method for removing salt-and-pepper noise from images. It is also used to remove noise generated occasionally because of sub pixel refinement. Filtering of disparity map can increase the accuracy of output. Thus in this way, coarse disparity map is generated.
Next step is to estimate region based disparity map. The chances of making an incorrect decision upon an area can be greatly reduced, as area contains more information compared to individual pixels. The precision of disparity map generation depends on how well the color segmentation step segments the image. The color segmentation technique has two hypotheses: a) in segmented areas disparity value changes smoothly; b) depth discontinuity occurs on edges only. First of all left image 
The segmentation based techniques makes it possible to match large textureless regions very well which is a considerable problem with area based stereo matching techniques. With the increase in the number of segments obtained by utilizing mean shift segmentation method time complexity also increases. The disparity map output is improved by removing noise in each area by using affine transformation, but non-smoothness exits among few neighboring areas due to over segmentation. Region merging is applied on the segmented image to solve this problem and to improve the output. Region merging merges the neighboring areas fulfilling similarity condition. Disparity maps generated are having smoothness within the segments and disparity discontinuity on the edges.
The first step in region based disparity estimation is to compute the disparity for the areas extracted in the preceding segmentation step. The segmented image and the coarse disparity map are the inputs to this step and each segment is assigned the median of the disparity values of the region pixels. All the pixels of each region are assigned same disparity value as it is supposed that pixels within the same region will have the same disparity. It is supposed that the coordinates 





Thus, the disparity 

Every pixel within the region gives one equation as in Equation (5). If the number of pixels within a region is N, then we will have N equations of (5) for this particular region. Mostly the number of pixels within region will be larger than the number of affine parameters e.g., three for 1-D affine transform. Therefore, the calculated 



Region based algorithms should be capable to deal with the segmentation errors. When the stereo image pair is segmented, errors may occur due to many factors like noise, bad imaging situations, over segmentation and limitations of segmentation procedure used. The mean shift algorithm segments the images utilizing color and intensity information and hence it produces more than one segment of the same object. Few homogeneous color regions are supposed to belong to the same planar or surface model, but due to over-segmentation approach they are separated in the partition label and we can refine the disparity map by assigning one universal disparity plane/surface to all of them. Grouping similar homogeneous color segments to extract their disparity layer can help in regions not having sufficient inliers because of noise or occlusion to get good plane/surface estimation by using affine. In such situations, more accurate points for the disparity estimation can be obtained by merging regions having similar disparities, resulting in to bigger regions.
Region merging is a method that groups two different segments into one segment based upon two conditions: proximity and homogeneity. Criterion is needed to take decision regarding which neighboring regions are good candidates to be merged. Two regions represented by the same set of model parameters can be successfully merged. The second criterion, homogeneity, is satisfied by a similarity measure that computes the similarity between regions and selects the optimal regions to be merged. We compute the intensity variation between all neighboring regions and if the difference value is less than threshold value than those corresponding regions are merged. In this technique, deciding the threshold value is an overhead.
The overview of the region merging [28] can be described as below: First of all region adjacency information is computed based on the current segmentation label. Thereafter a regions similarity measure is computed between neighboring regions. At last the best chosen region pair having best similarity measure is merged. This process merges regions iteratively, two regions at each iteration and always initiates by the most similar regions.
To facilitate in the region merging process matrix representation of the regions adjacency is created. Region Adjacency Matrix (RAM) is the lower triangle of a square table where rows and columns represent regions. If cell Cij is marked as true than it means that regions i and j are neighboring and if it is marked as false, than those regions are assumed not to be neighbors.
Finally, a multilateral filtering is applied on the disparity map obtained to preserve information and to smooth the disparity map in occluded regions at object boundary, discontinuous and textureless area to generate final disparity map as output.
4. Experimental Results & Discussion
In this section, we present and discuss the experimental results of our algorithm. The Middlebury dataset [1] [29] is used to evaluate the results of the proposed algorithm. The image pairs like Tsukuba, Teddy, Cones, Venus, and Sawtooth used for the evaluation purpose are popular and widely used by the stereo vision community. These stereo image pairs are well known for the combination of objects having different characteristics and are challenging for stereo matching. Computation of our proposed algorithm is carried out in Matlab on Intel(R) Core(TM) i3 CPU M 350 @ 2.27GHz (4 CPUs) laptop.
Figure 3(b) demonstrates coarse disparity map result obtained by using census transform for Tsukuba image pair. This coarse disparity map estimated and left mean segmented image are given as input to generate disparity map using affine transformation as shown in Figure 3(c), which computes disparity for each segment. We can observe that this kind of parameterized estimation process can give more reasonable results in which the noise in each region is somewhat eliminated, but still non-smoothness prevails between some neighboring regions due to over segmentation. Region merging is used to solve this problem of non-smoothness due to over segmentation and to refine the disparity map results. Region merging is applied on the segmented image and it merges the


Figure 3. (a) Left image of Tsukuba (b) coarse disparity generated by using census transform [4] (c) result after affine transformation (d) final disparity map estimated (e) disparity map generated by SAD (f) disparity map generated by using segmentation approach [30] .
neighboring regions fulfilling the similarity condition. However, few regions having occlusions give worse effects. Multilateral filtering is applied to solve this problem and final disparity map is estimated. Figure 3(d) shows disparity map generated after region merging and multilateral filtering, which clearly demonstrates improvement for most regions: smoothness in disparity within the segment and disparity discontinuity on the object boundaries.
A quantitative approach is required to assess the performance of a stereo matching algorithm by estimating the quality of the final disparity map generated. The quality of the estimated disparity map is determined with respect to the ground truth by utilizing similarity measure Root Mean Square Error (RMSE). RMSE is computed in terms of disparity units between the resultant disparity map 


where N is the total number of pixels.
The performance of the proposed algorithm is summarized in Table 1. Table 1 shows the calculated Root Mean Square Error (RMSE) of the final disparity maps estimated by our proposed approach with respect to the ground-truth disparity maps for four different stereo image pairs as shown in Figures 4.1-4.4. It also compares RMSE values obtained for different stereo image pairs for our proposed approach with the RMSE values obtained for sum of absolute difference (SAD), census based and segment based approach.

Figure 4.1. Results for Tsukuba image sequence (a) left input image (b) right input image (c) result of our proposed algorithm (d) ground truth.

Figure 4.2. Results for Cones image sequence (a) left input image (b) right input image (c) result of our proposed algorithm (d) ground truth.
Table 1. RMSE for stereo image pairs.

Figure 4.3. Results for Teddy image sequence (a) left input image (b) right input image (c) result of our proposed algorithm (d) ground truth.

Figure 4.4. Results for Venus image sequence (a) left input image (b) right input image (c) result of our proposed algorithm (d) ground truth.
From the Figure 3(b), Figure 3(d), Figure 3(f) and Table 1, it can be concluded that our census and segmentation based proposed approach gives better results compared to the results obtained by either of the approach alone. From Figure 3(d), Figure 3(e) and Table 1, it can be shown that the results of our proposed approach are also better than the results obtained by using (SAD).
The test images consist of regions having different characteristics like occluded, disparity discontinuous and textureless portion. Our proposed algorithm gives excellent disparity map results in all cases. From the results shown in Figures 4.1-4.4 and Table 1, it can be demonstrated that our proposed algorithm gives quality disparity map as output: disparity varies smoothly within segmented region and disparity discontinuities occurs on the object boundaries.
5. Conclusions & Future Work
This paper presents a novel, robust, efficient, and flexible stereo matching algorithm which combines census- based and region-based approach. The algorithm deals with rectified stereo image pair. It is shown that the segmentation based algorithm works well with the census-based algorithm. The originality of our algorithm lies in the fact that it offers a robust technique to solve few long standing problems in the disparity map generation like the smoothness of regions while keeping edges clear and sharp, occluded regions, textureless regions, repetitive patterns, perspective distortion, specular reflection, noise, disparity discontinuous regions. These issues cannot be solved by either approach independently. Census measures are appropriate for highly textured areas. It is also somewhat computationally complex. Census transform offers high resistance to noise as it is based on the relative ordering of local pixel intensity values. While segment based methods are popular for its excellent performance in dealing with textureless areas, edges and noise. The chances of making a wrong selection of disparity upon a segment is significantly lessen as segments enclose a large amount of information compared to individual pixels. It is shown that the segmentation based algorithm makes it possible to match the excellently large textureless region which is a major issue with standard area-based stereo matching techniques. Time complexity of algorithm increases with the increase in the number of segments which are obtained by utilizing mean shift segmentation approach.
Disparity map results are improved using affine transformation as it removes noise in each region, but non- smoothness prevails between some neighboring regions due to over segmentation. To solve this problem of non- smoothness we have applied region merging on the segmented image to refine the disparity map results. Region merging merges the neighboring areas satisfying the similarity condition. Disparity maps estimated are having smoothness within the segments and disparity discontinuity on the object boundaries. At last, multilateral filtering is applied on the disparity map generated to preserve information and to smooth the disparity map in occluded areas at edges, discontinuous and textureless regions to estimate final disparity map as output. Non parametric census transform works well in image areas having same colors and commonly used area based similarity measures like SAD and SSD produces quality results for image areas with similar local structures. The real-time application of our algorithm will be our future work. The proposed algorithm can be implemented using FPGA or GPU for hardware acceleration in future.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgements
The authors would like to convey gratitude to Daniel Scharstein and Richard Szeliski for providing stereo images with ground truth.
Cite this paper
Viral H.Borisagar,Mukesh A.Zaveri, (2015) Census and Segmentation-Based Disparity Estimation Algorithm Using Region Merging. Journal of Signal and Information Processing,06,191-202. doi: 10.4236/jsip.2015.63018
References
- 1. Scharstein, D. and Szeliski, R. (2002) A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. International Journal of Computer Vision, 47, 7-42.
http://dx.doi.org/10.1023/A:1014573219977 - 2. Fua, P. (1993) A Parallel Stereo Algorithm That Produces Dense Depth Maps and Preserves Image Features. Machine Vision and Applications, 6, 35-49. http://dx.doi.org/10.1007/BF01212430
- 3. Scharstein, D. and Szeliski, R. (1996) Stereo Matching with Non-Linear Diffusion. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 28, 343-350.
http://dx.doi.org/10.1109/CVPR.1996.517095 - 4. Zabih, R. and Woodfill, J. (1994) Non-Parametric Local Transforms for Computing Visual Correspo-ndence. Proceedings of Third European Conference of Computer Vision, 801, 151-158.
- 5. Zitnick, C.L. and Kang, S.B. (2007) Stereo for Image-Based Rendering using Image Over-Segment-ation. International Journal of Computer Vision, 75, 49-65.
http://dx.doi.org/10.1007/s11263-006-0018-8 - 6. Wei, Y. and Quan, L. (2004) Region-Based Progressive Stereo Matching. Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1, 106-113.
- 7. Birchfield, S. and Tomasi, C. (1999) Multiway Cut for Stereo and Motion with Slanted Surfaces. Proceedings of the 7th IEEE International Conference on Computer Vision, 1, 489-495.
http://dx.doi.org/10.1109/ICCV.1999.791261 - 8. Hirschmuller, H. and Scharstein, D. (2007) Evaluation of Cost Functions for Stereo Matching. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, 17-22 June 2007, 1-8. http://dx.doi.org/10.1109/cvpr.2007.383248
- 9. Scharstein, D. (1994) Matching Images by Comparing Their Gradient Fields. Proceedings of the 12th IAPR International Conference on Pattern Recognition, 1, 572-575.
http://dx.doi.org/10.1109/ICPR.1994.576363 - 10. Seitz, P. (1989) Using Local Orientation Information as Image Primitive for Robust Object Recog-nition. SPIE Visual Communications and Image Processing IV, 1199, 1630-1639.
http://dx.doi.org/10.1117/12.970173 - 11. Hirschmuller, H. and Scharstein, D. (2009) Evaluation of Stereo Matching Costs on Images with Radiometric Differences. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31, 1582-1599.http://dx.doi.org/10.1109/TPAMI.2008.221
- 12. Lee, Z., Juang, J. and Nguyen, T.Q. (2013) Local Disparity Estimation with Three-Moded Cross Census and Advanced Support Weight. IEEE Transactions on Multimedia, 15, 1855-1864.
http://dx.doi.org/10.1109/TMM.2013.2270456 - 13. Gautama, S., Lacroix, S. and Devy, M. (1999) Evaluation of Stereo Matching Algorithms for Occupant Detection. Proceedings of the International Workshop on Recognition, Analysis, and Tracking of Faces and Gestures in Real-Time Systems, Corfu, 26-27 September 1999, 177-184.
http://dx.doi.org/10.1109/RATFG.1999.799242 - 14. Banks, J. and Corke, P. (1991) Quantitative Evaluation of Matching Methods and Validity Measures for Stereo Vision. IEEE International Journal of Robotics Research, 20, 512-532.
http://dx.doi.org/10.1177/02783640122067525 - 15. Hirschmller, H. (2001) Improvements in Real-Time Correlation Based Stereo Vision. Proceedings of the IEEE Workshop on Stereo and Multi-Baseline Vision, Kauai, 9-10 December 2001, 141-148.
http://dx.doi.org/10.1109/SMBV.2001.988772 - 16. Humenberger, M., Engelke, T. and Kubinger, W. (2010) A Census-Based Stereo Vision Algorithm Using Modified Semi-Global Matching and Plane Fitting to Improve Matching Quality. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), San Francisco, 13-18 June 2010, 77- 84. http://dx.doi.org/10.1109/CVPRW.2010.5543769
- 17. Tsai, T.H., Nelson Chang, Y.C., Tseng, Y.C. and Chang, T.S. (2007) Census Diffusion with Segment Constraint for Disparity Estimation in Stereo Vision. Proceedings of the Computer Vision, Graphics and Image Processing (CVGIP), Taiwan, 19-21 August 2007.
- 18. Xiao, J., Xia, L.Y., Lin, L.Q. and Zhang, Z.T. (2010) A Segment-Based Stereo Matching Method with Ground Control Points. Proceedings of the 2nd Conference on Environmental Science and Infor-mation Application Technology, Wuhan, 17-18 July 2010, 306-309.
- 19. Hong, L. and Chen, G. (2004) Segment-Based Stereo Matching Using Graph Cuts. Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1, 74-81.
http://dx.doi.org/10.1109/CVPR.2004.1315016 - 20. Bleyer, M. and Gelautz, M. (2005) Graph-Based Surface Reconstruction from Stereo Pairs Using Image Segmentation. Proceedings of SPIE 5665, Video Metrics VIII, 5665, 288-299.
- 21. Klaus, A., Sormann, M. and Karner, K. (2006) Segment Based Stereo Matching Using Belief Propagation and a Self-Adapting Dissimilarity Measure. Proceedings of the International Conference on Pattern Recognition, Hong Kong, 20-24 August 2006, 15-18.
http://dx.doi.org/10.1109/icpr.2006.1033 - 22. Huang, X.D. and Dubois, E. (2006) 3D Reconstruction Based on a Hybrid Disparity Estimation Algorithm. Proceedings of the IEEE International Conference on Image Processing, Atlanta, 8-11 October 2006, 1025-1028.http://dx.doi.org/10.1109/icip.2006.312674
- 23. Comanicu, D. and Meer, P. (2002) Mean Shift: A Robust Approach toward Feature Space Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 603-619.
http://dx.doi.org/10.1109/34.1000236 - 24. Yin, Y., Jin, M. and Xie, S.Y. (2010) A Stereo Pairs Disparity Matching Algorithm by Mean-Shift Segmentation. Proceedings of the Third International Workshop on Advanced Computational Intelligence, Suzhou, 25-27 August 2010, 639-642. http://dx.doi.org/10.1109/IWACI.2010.5585232
- 25. Wang, Z.-F. and Zheng, Z.-G. (2008) A Region Based Stereo Matching Algorithm Using Cooperative Optimization. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, 23-28 June 2008, 1-8.
- 26. Manduchi, R. and Tomasi, C. (1998) Bilateral Filtering for Gray and Color Images. Proceedings of the IEEE International Conference on Computer Vision, Bombay, 4-7 January 1998, 836-846.
- 27. Bobick, A.F. and Intille, S.S. (1999) Large Occlusion Stereo. International Journal of Computer Vision, 33, 181-200.http://dx.doi.org/10.1023/A:1008150329890
- 28. Wang, X. (2009) Disparity Estimation Using a Color Segmentation. Master’s Dissertation, Universitat Politecnica De Catalunya, Barcelona.
- 29. http://vision.middlebury.edu/stereo/
- 30. Borisagar, V.H. and Zaveri, M.A. (2011) A Novel Segment-Based Stereo Matching Algorithm for Disparity Map Generation. Proceedings of the 2011 International Conference on Computer and Software Modeling, 14, 25-29.




















