Journal of Signal and Information Processing
Vol.05 No.02(2014), Article ID:45577,8 pages
10.4236/jsip.2014.52005
Template Matching from 2-D into 1-D
Yasser Fouda1,2
1College of Computer Science and Information Technology, King Faisal University, Al-Ahsa, KSA
2Mathematics Department, Faculty of Science, Mansoura University, Mansoura, Egypt
Email: yfoudah@kfu.edu.sa
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 January 2014; revised 4 February 2014; accepted 15 February 2014
ABSTRACT
This paper proposes a 1-D template matching algorithm for finding the exact best match for a template image in a source image. The basic idea depends on converting the template and all candidate blocks in the source from 2-D into 1-D. Three different similarity measures in template matching can be used to compute the likeness between the template and blocks. This algorithm can be considered as an alternative for 2-D full search block matching and it achieves a good computational cost. Complexity analysis and experimental results show that the performance of the proposed is superior to that of other basic template matching algorithms.
Keywords:
Image Processing, Template Matching, Similarity Measures, Image Dimensions Reduction

1. Introduction
Template matching is an important technique in pattern recognition and image processing. It is used in many applications related to signal processing and machine vision such as object tracking, stereo matching, video compression, image retrieval and image registration. Template matching tries to answer one of the most basic questions about image: Is there a certain object in that image? If so, where it is? The template is a description of that object, and is used to search the image by computing a different measure between the template and all possible portions of the image that could match the template. If any of these produces a small difference, then it is viewed as possible occurrence of the object [1] .
Various different measures have different mathematical properties, and different computational properties have been used to find the best match. The most popular similarity measures are the sum of absolute differences (SAD), the sum of squared difference (SSD), and the normalized cross correlation (NCC). Because SAD and SSD are computationally fast and algorithms are available which make the template search process even faster, many applications of gray-level image matching use SAD or SSD measures to determine the best match. However, these measures are sensitive to outliers and are not robust to variations in the template, such as those that occur at occluding boundaries in the image. However, the NCC measure is more accurate but it is computationally slow. It is more robust than SAD and SSD under uniform illumination changes, so the NCC measure has been widely used in object recognition and industrial inspection such as in [2] [3] . An empirical study of five template matching algorithms in the presence of various image distortions has found that NCC provides the best performance in all image categories [4] .
Many improvements were occurred on SAD and NCC algorithms to get a better complexity. Mahmood and Khan [5] proposed a partial computation elimination technique in which at a particular search location, computations are prematurely terminated as soon as it is, and found that this location cannot compete already known best-match location. They showed that partial elimination technique may be applied to correlation coefficient by using a monotonic formulation and proposed a basic mode for small template size and an extended mode for medium and larger template. Chen et al. [6] proposed a fast block matching algorithm based on the winner-update strategy, which can significantly reduce the computation and guarantee to find the globally optimal solution. In their algorithms, only the current winner location with a minimal accumulated distortion is considered for updating the accumulated distortion. This updating process is repeated until the winner has gone through all levels in the pyramids that are constructed from the template and all the candidate windows for the distortion calculation.
Wei and Lai [7] proposed a fast pattern matching algorithm based on NCC criterion by combing adaptive multilevel partition with the winner update scheme to achieve very efficient search. This winner update scheme is applied in conjunction with an upper bound for the cross correlation derived from Cauchy-Schwarz inequality. To apply the winner update scheme in an efficient way, they partition the summation of cross correlation into different levels with the partition order determined by the gradient energies of the partitioned regions in the template. Thus, this winner update scheme in conjunction with the upper bound for NCC can be employed to skip unnecessary calculation. Alsaadeand Fouda [8] used Cellular Automata with Rule 170 (CA-R170) on the images after converting it into binary images. Your technique is based on eliminating some of the undesirable areas in the binary source images and their corresponding binary template images. Essannouni et al. [9] proposed a frequency algorithm to speed up the process of SAD matching using Fast Fourier transforms (FFT). They introduced an approach to approximate the SAD metric by cosine series which can be expressed in correlation terms. These latter can be computed using FFT algorithms. Alsaade and Fouda [10] proposed a matching algorithm based on SAD as a measure of similarity and pyramid structure. They applied the pyramid concept to obtain a number of levels of original and template images. Then the SAD measure is applied for each level of image from bottom to up to obtain the correct match in the original image.
In this paper, we propose an efficient pattern search algorithm based on Dimension-Reduction approach for images. Dimension-Reduction technique is applied for the template image and all corresponding sub-windows in the source image. In our approach, Dimensions-Reduction technique is based on converting the template and all its corresponding sub-windows in the source from 2-D into 1-D. The sum of square difference measure was used as a similarity measure to get the template in the source. The rest of the paper is organized as follows. The proposed algorithm and its complexity analysis are described in Section 2. Simulation and comparison results for NCC and SAD standards are reported in Section 3. Then we state conclusions in Section 4.
2. The Main Contribution
In this section we introduce description of the proposed method followed by its complexity analysis compared with other four methods.
2.1. The Proposed Method
Our method has been motivated by a need to develop an efficient matching technique so that the detection of objects in a source image can be effective and fast. The proposed matching algorithm involves three phases. Phase I reduces the amount of data analyzed by transforming 2-D images (template image and sub-windows which has the same size with template in the source image) into 1-D vector information. This can be done by adding all intensity values for each column in 2-D image see Equation (1), so we get 1-D vector information. This vector information will be used in the matching process instead of the 2-D image. This transforming reduces the amount of image from m × n to n. Subsequently, this allows the search to be performed with fewer data, while still taking all pixel intensity values into account. Phase II measures the likeness between template image and all possible sub-windows in the source image. The Euclidean distance or sum of absolute difference or sum of square difference can be used as a similarity measure between 1-D template and all 1-D converted sub-window in the source. Phase III the decision will be taken based on the similarity values. The sub-window in the source with minimum similarity value will be the best match for template in the source.
The basic idea of the proposed template matching depending on converting 2-D template image into 1-D and also the corresponding windows in the source image over which the template lies. To illustrate the idea suppose that we have a source image S of size p × q and template image T of size m × n where m < p and n < q. The problem is to find the best match of template T from the source image S with minimum distortion.
First the template image T(i,j) converted to 1-D vector NT by the equation
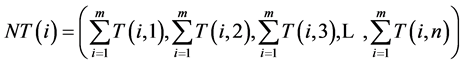 (1)
(1)
where T(i,j) is the pixel value at location (i,j) of the template image.
Secondly, for each pixel (i,j) in the source image S, 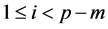 and
and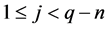 , we determine a window W(i,j) of size m × n and all these windows converted into 1-D vector NW by the equation
, we determine a window W(i,j) of size m × n and all these windows converted into 1-D vector NW by the equation
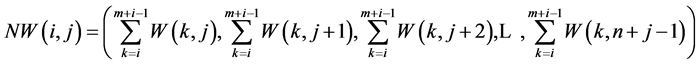 (2)
(2)
where W(k,j) is the pixel value at location (k,j) of the source image.
Thirdly, the likeness between template image and each corresponding window in the source are measured by sum of square difference distance between NT and NW. All these distances compute and store in new storage C(i,j) where
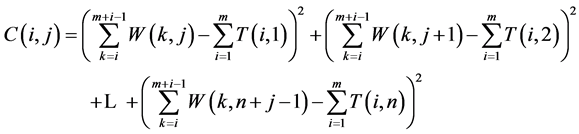 (3)
(3)
where 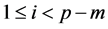 and
and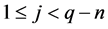 .
.
If the positive ordered pair  be such that
be such that 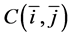 is the lowest obtained distance, then return
is the lowest obtained distance, then return 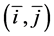 as the left upper corner of best template match in our proposed method.
as the left upper corner of best template match in our proposed method.
2.2. Complexity Analysis
In order to evaluate the efficiency of the proposed algorithm, we discuss the complexity of our algorithm compared with four important methods of template matching NCC, SAD, NCCP, and SADP. For NCC algorithm, the cross correlation coefficient between template image T of size n × n pixels and an n × n pixels block in source image S of size p × q is given by:
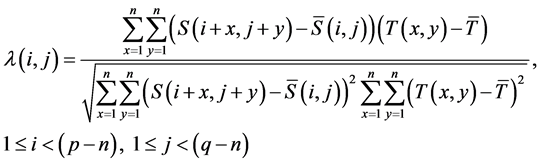 (4)
(4)
where
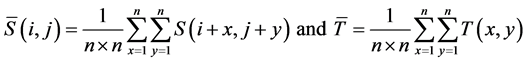
Direct computation of λ(i,j) require n × n = n2 (addition/multiplication) operations at each point (i,j) in the source image where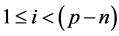 ,
,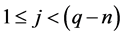 . Then the operations in Equation (4) is proportional to
. Then the operations in Equation (4) is proportional to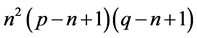 . So the computational cost of NCC is
. So the computational cost of NCC is 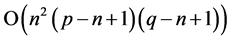 which is very time consuming.
which is very time consuming.
For SAD method the sum of absolute difference between the template T of size n × n pixels and blocks of sizes n × n pixels in the source image S is given by:

The computation of 



The two methods NCCP and SADP can achieve the same estimation accuracy as NCC and SAD while needing much less computation requirement than theses two methods. When the pyramid is applied for NCC and SAD, a sequence of compressed template and source images are created using:

where Ik(x,y) is the intensity value for the image in the level k. The search is conduct using NCC or SAD (Equations (4) or (5)) with the most compressed template and source image. The resulting pixel location provides a coarse location of the template pattern in the next lower level of the source image. Therefore, instead of performing a complete search in the next level, one require to only search a close neighborhood of the area computed from the previous search. This sequence is iterated until the search in the source image is searched.
In the pyramid concept the complexity of the algorithm depend on the position of template in the source. If the template coordinates is far from the x-direction and y-direction then applying pyramid outperform the original method. But, if the x-coordinate for template in source is close to x-axis and/or y-coordinate for template in source is close y-axis the original method outperform the pyramid concept.
To overcome the problem in pyramid concept and the computational intensive in NCC and SAD we introduced our approach. The computation in Equation (3) require a number of operations proportional to the length n of the converted vector from 2-D into 1-D. These operations are computed for each position (i,j) in the source image where


3. Experimental Results
To measure the efficiency the proposed method was implemented. For the comparing purpose, we also implemented four different algorithms the full-search NCC algorithm, NCC pyramid (NCCP) algorithm, sum of absolute difference (SAD) algorithm, and SAD pyramid (SADP) algorithm. Theses algorithms were implemented in a Matlab 7.0 on a Laptop with an Intel® Core™2 Duo CPU T7500 @ 2.20 GHz and 1.99 GB RAM. Two types of images are used for the testing purpose color images and gray scale images. Greens image of size 300 × 500 is a representative for color case see Figure 1(a). Lifting-body of size 512 × 512 is a representative for gray scale case, see Figure 2(a). In our experiments we cropped the templates from the source (see Figure 1(b) and Figure 2(b)) so we know in advance the correct position for template in the source. The size of these templates varies from 25 × 25 to 200 × 200 pixels.
In the clean data, the proposed and compared algorithms are guaranteed to find the correct match from the source image, so we only focus on the comparison of search time required for these algorithms. In the proposed method the similarity between template and sub-windows in the source image can be measure using more than one similarity function. For example the Euclidean distance or sum of absolute difference or sum of square difference can be used. The mathematical formula for sum of square difference is used in our method (see Equation (3)). To apply the Euclidean distance and sum of absolute difference functions in our method their mathematical formula is given by the following equations respectively.


Figure 1. (a) Original greens image; (b) The cropped template images form the original with sizes varying from 25 × 25 to 150 × 200 pixels.


Figure 2. (a) Original Lifting-body image; (b) The cropped template images from the original with sizes varying from 25 × 25 to 200 × 200 pixels.

and

Figure 3 and Figure 4 compare between the three similarity functions for the images greens and lifting-body, respectively. In this comparing we taken five template with different sizes from each source and computing the time confused by each similarity function in our proposed method. As can be seen from Figure 3, SSD function outperforms Euclidean and SAD functions but the required time of the three functions is almost the same at template of sizes 25 × 25 and 150 × 150. Also, from Figure 4, we can see that SSD function outperform Euclidean and SAD functions but the required time for the three functions is almost the same at template of sizes 25 × 25 and 200 × 200. Finally, from these two figures, we can see that for the two kind of images the SSD functions is the best because the number of operations of SSD is less than the number of operations in SAD and Euclidean (see Equations (3), (7) and (8)).
The execution time required for the proposed and compared algorithms is shown in Table 1 and Table 2. These Tables shows the performance comparison of the above mentioned algorithms using color image of size
Figure 3. Comparisons between the three similarity functions on greens image using different size of template.
Figure 4. Comparisons between the three similarity functions on lifting-body image using different sizes of template.
Table 1. Execution time by seconds of applying NCC, NCCP, SAD, SADP, and proposed method with five templates shown in Figure 1(b) and the source image show in Figure 1(a).
Table 2. Execution time by seconds of applying NCC, NCCP, SAD, SADP, and proposed method with five templates shown in Figure 2(b) and the source image show in Figure 2(a).
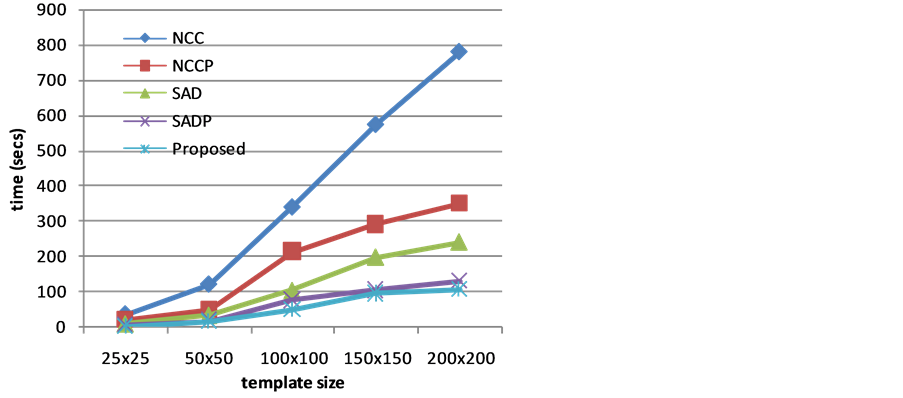
300 × 500 and gray scale image of size 512 × 512 respectively. For each source image the templates are cropped with sizes from 25 × 25 to 200 × 200. From these Tables we see that the times in Table 1 is less than its corresponding times in Table 2 because the size of source image in Table 1 and Table 2 are 150000 and 262141 pixels respectively. In Table 1 the running time for NCCP and SADP algorithms for 150 × 150 template is greater than 200 × 200 template although the converse must be satisfied. This result is because that the 150 × 150 template is very close the y-direction in greens image. NCCP and SADP give a better result than NCC and SAD when the template is far from the x-direction and y-direction in the source image.
From Table 1, it is clarified that the processing time for the proposed is less than that for NCC, NCCP, SAD, and SADP. For example, using the 50 × 50 template, the processing time for the proposed was 7.7 s, however, NCC, NCCP, SAD, and SADP matching required 56.58, 42.25, 16.66, and 14.19 s respectively. This means that the proposed give an improvement at least about 50%. Also from Table 2 the required time of the proposed is better than another all algorithms for all templates. Since the complexity of the proposed is more efficient than the other methods. Figure 5 and Figure 6 show the performance of the proposed algorithm compared with other four algorithms using greens image (color case) and lifting-body (gray scale case) respectively. It is clear that the proposed algorithm outperform the other in the two cases for all template sizes. In the above experiments, the correct match position is assumed to be the position where the minimum similarity distance value is obtained when the entire template is used in the search process.
4. Conclusion
In this paper, we have proposed a new template matching which can speed up the computation of block matching while still guarantee the correct match for template in the source. To achieve efficient computation, we converted the template and each corresponding block in the source from 2-D into 1-D. We have applied the proposed idea to the template matching using three different similarity measures, and it has a reduction in computation time. Two different types of image (color and gray scale) are used for comparison between proposed algorithm and other algorithms. The templates are cropped from the source image. The experimental results
Figure 5. Performance of the proposed algorithm using greens image.
Figure 6. Performance of the proposed algorithm using lifting-body image.
show that the proposed algorithm is efficient for pattern matching under uniform illumination.
References
- Mikhail, I.A. (2001) Faster Image Template Matching in the Sum of the Absolute Value of Differences Measures. IEEE Transactions on Image Processing, 10, 659-663.
- Tsai,D.-M. and Lin, C.-T. (2003) Fast Normalized Cross Correlation for Detect Detection. Pattern Recognition Letters, 24, 2625-2631. http://dx.doi.org/10.1016/S0167-8655(03)00106-5
- Costa, C.E. and Petrou, M. (2000) Automatic Registration of Ceramic Tiles for the Purpose of Fault Detection. Machine Vision and Applications, 11, 225-230. http://dx.doi.org/10.1007/s001380050105
- Li, R., Zeng, B. and Liou, M.L. (1994) A New Three-Step Search Algorithm for Block Motion Estimation. IEEE Tran- sactions on Circuits and Systems for Video Technology, 4, 438-442. http://dx.doi.org/10.1109/76.313138
- Mahmood, A. and Khan, S. (2012) Correlation Coefficient Based Fast Template Matching through Partial Elimination. IEEE Transactions on Image Processing, 21, 2099-2108. http://dx.doi.org/10.1109/TIP.2011.2171696
- Chen, Y.S., Huang, Y.P. and Fuh, C.S. (2001) A Fast Block Matching Algorithm Based on the Winner-Update Strategy. IEEE Transactions on Image Processing, 10, 1212-1222. http://dx.doi.org/10.1109/83.935037
- Wei, S. and Lai, S. (2008) Fast Template Matching Based on Normalized Cross Correlation with Adaptive Multilevel Winner Update. IEEE Transactions on Image Processing, 17, 2227-2235. http://dx.doi.org/10.1109/TIP.2008.2004615
- Alsaade, F., Fouda, Y. and Khan, A.R. (2012) Efficient Cellular Automata Algorithm for Template Matching. Journal of Artificial Intelligence, 5, 122-129. http://dx.doi.org/10.3923/jai.2012.122.129
- Essannouni, F., Thami, R.O.H., Aboutajdine, D. and Salam, A. (2007) Adjustable SAD Matching Algorithm Using Frequency Domain. Journal of Real-Time Image Processing, 1, 257-265. http://dx.doi.org/10.1007/s11554-007-0026-0
- Alsaade, F. and Fouda, Y. (2012) Template Matching Based on SAD and Pyramid. International Journal of Computer Science and Information Security, 10, 11-16.