Journal of Signal and Information Processing
Vol.5 No.3(2014), Article
ID:48300,17
pages
DOI:10.4236/jsip.2014.53009
Survey of Surface Reconstruction Algorithms
Amin Alqudah
Computer Engineering Department, Hijjawi Faculty for Engineering Technology, Yarmouk University, Irbid, Jordan
Email: amin.alqudah@yu.edu.jo
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2013; revised 15 May 2013; accepted 7 June 2013
Abstract
Surface reconstruction is a problem in the field of computational geometry that is concerned with recreating a surface from scattered data points sampled from an unknown surface. To date, the primary application of surface reconstruction algorithms has been in computer graphics, where physical models are digitized in three dimensions with laser range scanners or mechanical digitizing probes (Bernardini et al., 1999 [1] ). Surface reconstruction algorithms are used to convert the set of digitized points into a wire frame mesh model, which can be colored, textured, shaded, and placed into a 3D scene (in a movie or television commercial, for example). In this paper, we discuss some computational geometry preliminaries, and then move on to a summary of some different techniques used to address the surface reconstruction problem. The coming sections describe two algorithms: that of Hoppe, et al. (1992 [2] ) and Amenta, et al. (1998 [3] ). Finally, we present other applications of surface reconstruction and a brief comparison for some algorithms in this filed emphasizing on their advantages and disadvantages.
Keywords:Surface Reconstruction, Convex Hull, Delaunay Triangulation

1. Introduction
Computational geometry can be described as the field of study concerned with the design and implementation of algorithms used for the efficient solution of geometric problems (O’Rourke, 1998 [4] ). Three core interests in computational geometry involving a set of points in Rn (the set of real numbers in n-dimensional space) are the convex hull, the Delaunay triangulation, and the Voronoi diagram.
1.1. The Convex Hull
The convex hull of a set of points S is the unique convex polytope (polygon in 2D, polyhedron in 3D) that contains S and also has points of S as its vertices (de Berg et al., 1997 [5] ). Intuitively, one could imagine a set of pushpins, each corresponding to a point in R2, in a corkboard; a string wrapped tightly around the outermost boundary of the pushpins is the two-dimensional convex hull of the set of points represented by the pushpins.
1.2. The Delaunay Triangulation
It is often desirable to connect a set of points S in R2 into a triangular network or mesh, which is called a triangulation of S. There are many possible triangulations for a given set of points; of special interest is the Delaunay triangulation. The 2D Delaunay triangulation has many useful properties:
1) It is a connected graph;
2) It is the dual of the Voronoi diagram;
3) No vertices are contained within the circumcircle (the unique circle containing a triangle’s three vertices) of any triangle in the mesh;
4) It is the configuration with the “fattest” possible set of triangles, i.e. with triangles most closely approaching an equilateral shape;
5) The boundary of the Delaunay triangulation is equal to the convex hull of the vertices of the mesh;
6) The Delaunay triangulation of a set of points is unique if, for each triangle in the mesh, no more than three vertices lie on the circumcircle of the triangle.
See Figure 1 for an illustration of the Delaunay triangulation of a set of points in 2D.
The Delaunay triangulation can be extended to higher dimensions, in which case the mesh is a network of simplices. In three dimensions, for example, the mesh is made up of tetrahedra (a tetrahedron is a 2-simplex). All of the above properties hold with the following generalizations to items 3, 4, and 6:
3’. no vertices are contained within the circumsphere (the unique sphere or hypersphere containing a simplex’s vertices) of any simplex in the mesh4’. it is the configuration with the “fattest” possible set of simplices, i.e. with simplices most closely approaching an equilateral shape6’. the Delaunay triangulation of a set of points is unique in Rn if, for each simplex in the mesh, no more than n vertices lie on the circumsphere of the simplex.
1.3. The Voronoi Diagram
Given a set of points S in Rn, it is sometimes useful to subdivide space into regions in which all points in a given

Figure 1. Two-dimensional Delaunay Triangulation of a set S of points. Red: Delaunay triangulation edges. Green: Delaunay triangulation vertices (points in S). [http://www.cs.colorado.edu/~lizb/topology-defs.html].
region are closer to one point in S than to any other point in S. Such a subdivision is called the Voronoi diagram (sometimes referred to as the Voronoi tessellation) of S (de Berg, et al., 1997 [5] ). See Figure 2.
It was previously mentioned that the Voronoi diagram is the dual of the Delaunay triangulation. Technically, this is the case (in two dimensions) only if no four (or more) points of S lie on a circle (de Berg, et al., 1997 [5] ). If this condition is met, then given a Voronoi diagram V and a Delaunay triangulation D of a set of points S in R2:
• For each edge D, there is a corresponding edge in V.
• Each edge of D is bisected by the line containing an edge of V.
• There is a triangular face of D for each vertex of V.
• The center of each circumcircle of a triangle D is a vertex of V.
As shown in Figure 3, these rules extend readily to higher dimensions. For instance, in three dimensions the center of each circumsphere of a tetrahedron in D is a vertex of V.
2. Survey of Surface Reconstruction Algorithms
In this section we present a brief summary of several different approaches to solving the problem of surface reconstruction. Many techniques have been proposed and we do not attempt to be comprehensive in our review. Rather, we will focus on a handful of the more important algorithms put forth to date.
All of the surface reconstruction algorithms we looked at attempt to solve the surface reconstruction problem in R3. All are methods consisting of a number of fundamental algorithms, many of which are well-known (for instance computation of the Delaunay triangulation, Voronoi diagrams, convex hull, minimum spanning tree, etc.). Most researchers try to solve the general surface reconstruction problem, which is to produce a surface that is a reconstruction or an approximation of the unknown surface, given a set of scattered (unorganized) points sampled on the unknown surface and no other information. Other approaches require additional input. For example Hoppe, et al.’s (1992 [2] ) method uses information about the sampling process (accuracy and density) and the algorithm of Crossno and Angel (1999 [6] ) takes surface normal and sample point neighbor information as supplementary input.
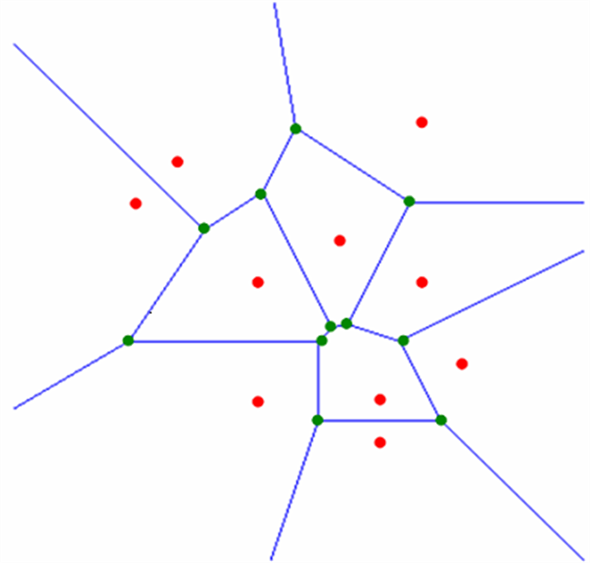
Figure 2. Two-dimensional Voronoi diagram of a set S of points. Blue: Voronoi edges. Red: Points in S. Green: Voronoi vertices. [http://www.cs.colorado.Edu/~lizb /topology-defs.html]
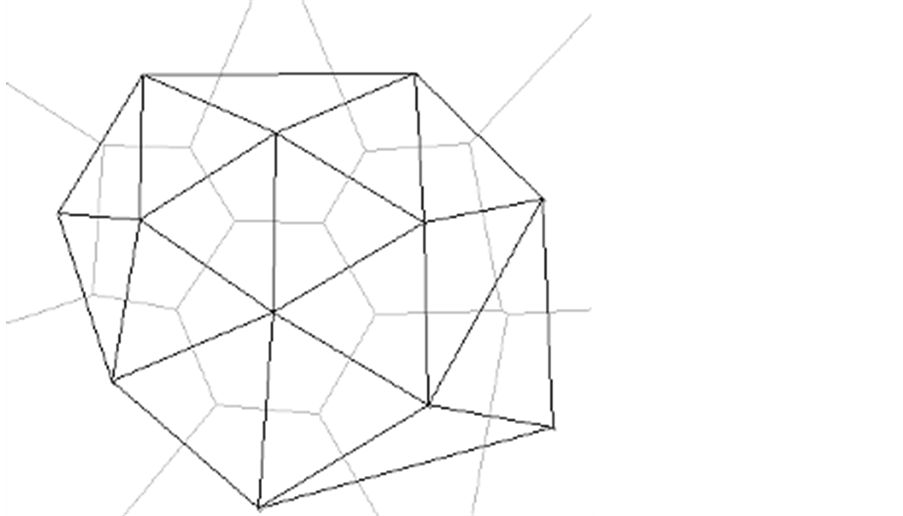
Figure 3. Voronoi/Delaunay duality. [http://www.ead.eee.ufmg.br/~renato/geocomp/delaunay/92.html]
2.1. Boissonnat, 1984 [7]
In an early paper on the subject of surface reconstruction, Boissonnat (1984 [7] ) proposed two different techniques. His first approach, which he describes as being surface-based, is locally two-dimensional. The algorithm starts by computing the k nearest neighbors (where k is an input parameter to the algorithm) of each sample point. This is accomplished through the use of a k-d tree (see Bentley and Friedman, 1979 [8] for details concerning k-d trees). An arbitrarily chosen starting edge connecting two k-neighbors is set to the current edge. The local tangent plane to the surface at the current edge is approximated by a least-squares plane through the neighbors of the endpoints of the current edge. Edges are added according to a rule that chooses points from the list of k-neighbors and locally preserves Delaunay angle properties when points are orthographically projected onto the approximate tangent plane. At each step, edges are added and the tangent plane is updated. The process continues until all sample points have been added to the triangulated edge structure. Boissonnat asserted that this method is valid provided the density of samples at any point on the surface is less than the radius of curvature at that point. The main problem with Boissonnat’s approach is that it is not robust with datasets that are sparse and non-uniform (Boissonnat and Cazals, 2000).
The second algorithm suggested by Boissonnat in his 1984 [7] paper takes a volumetric approach. The first step is to construct a three-dimensional Delaunay triangulation of the sample points. Next, tetrahedra are culled from the triangulation according to the following rule, as stated on his paper:
“The only tetrahedra that can be eliminated are those with exactly one face, three edges and three points on P, or those with exactly two faces, five edges and four points on P.”
Where P is the boundary of the polyhedral shape obtained by removing tetrahedra from the Delaunay triangulation. After culling, P is output as a piecewise linear reconstruction of the unknown surface (i.e., a triangular mesh). Boissonnat calls the culling process “sculpturing”. The biggest drawback to the sculpturing approach is that it is possible that some sample points may still remain inside of P upon termination of the algorithm (Bernardini, et al., 1999 [1] ).
Hoppe, et al. (1992 [2] ) take a fundamentally different approach to solving the surface reconstruction problem. Their method attempts to approximate the unknown surface rather than reconstructing it in piecewise linear fashion. The algorithm defines a signed distance function at each sample point and then contours the zero-set of the function using the Marching Cubes algorithm (for an explanation of this algorithm, see Lorensen and Cline, 1987 [9] ). The method of (Hoppe, et al.) will be described in detail in Section 3.0 of this paper.
2.3. Amenta, et al., 1998 [3]
The surface reconstruction method of Amenta, et al. (1998 [3] ) is similar to Boissonnat’s sculpturing algorithm. They also construct a three-dimensional Delaunay triangulation of the dataset, but not before augmenting it with one or two “poles” per sample point. The poles are selected from the set of Voronoi vertices. The output mesh, which they call the “crust” of the sample points, is guaranteed to be topologically correct provided the sampling density is adequate. This algorithm will be explained in much greater depth in Section 4.0 of this paper.
2.4. Other Surface Reconstruction Algorithms
The algorithm of Boissonnat and Cazals (2000 [10] ) combines the zero-set and Voronoi techniques, and produces a smooth surface that passes through all sample points. However their method requires the additional input of a normal value at each sample point. Crossno and Angel’s (1999 [6] ) Spiraling Edge algorithm takes sample data plus normal and nearest neighbor information as input. The authors assert that their specialized approach is three orders of magnitude faster than general-purpose surface reconstruction algorithms. In 2001, Carr, et al. [11] presented a new surface reconstruction algorithm that represents the unknown surface as the zero-set of a polyharmonic radial basis function. Their method is well suited for very large datasets (hundreds of thousands or even millions of sample points).
3. The Zero-Set Algorithm of Hoppe, et al.
Hoppe, et al. (1992 [2] ) address the problem of reconstructing a surface from unorganized points without using any other knowledge of the sampled surface (such as neighbor or normal information). They offer no guarantees of convergence or correctness for their algorithm, but they claim that it works well in practice. Their method is called a zero-set algorithm because it approximates a surface formed by the set of points that have a signed distance of zero to the surface.
3.1. Required Sampling Information
Although the algorithm requires no information about the sample points other than their coordinates, it does require knowledge of the sampling process. Two sampling parameters are employed:
• Noise magnitude δ: the maximum sampling error; for example the accuracy of a laser scanner.
• Sampling density ρ: the radius of a sphere, such that any sphere with radius ρ and center o in the unknown surface M contains at least one sample point. Intuitively, ρ represents the radius of the maximum “hole” in the sampled dataset.
Figure 4 shows the original object used by Hoppe et al. to illustrate their algorithm and Figure 5 shows the points that were sampled from this object.
3.2. Tangent Plane Computation
The first step of the algorithm is to estimate a tangent plane at each sample point. The tangent planes approximate the tangent to the unknown surface M at each of the sample points. A k-neighborhood is defined as the k closest points surrounding a sample point, where k is a user-specified parameter. Tangent planes are computed at by fitting a least-square plane through points in the k-neighborhood of each sample point. Tangent planes are represented by their center point o and by their normal vector n.
3.3. Tangent Plane Orientation
The next phase of the algorithm is to find a consistent orientation for the tangent planes. All tangent plane normal vectors must point away from the object. Therefore, it is necessary to flip tangent plane normal vectors that point in the wrong directions. The first step in orienting the tangent planes is to compute the Euclidean Minimum Spanning Tree (Euclidean MST or EMST) of the graph connecting the tangent plane centers (oi). The
Euclidean MST is a minimum spanning tree of a connected graph with weights equal to the Euclidean lengths of its edges as shown in Figure 6. The authors found that the EMST is insufficiently dense in edges for tangent plane orientation to work properly. To solve this problem, they enrich the EMST by adding edges corresponding to the tangent plane centers that are in the same k‑neighborhood. The resulting graph is called the Riemannian Graph and it is illustrated in Figure 7.
Normal-flipping takes place during traversal of the Riemannian Graph. Therefore, the graph should be traversed along a set of paths that prefers edges between tangent planes that are most closely parallel. To accomplish this, Riemannian Graph edge weights are defined as , so that the cost will be small if the planes are almost parallel. The MST of the Riemannian Graph is based on the weight values defined as just described; see Figure 8. The root of the MST of the Riemannian Graph is assigned to the tangent plane center with the
, so that the cost will be small if the planes are almost parallel. The MST of the Riemannian Graph is based on the weight values defined as just described; see Figure 8. The root of the MST of the Riemannian Graph is assigned to the tangent plane center with the
largest z coordinate. The root’s tangent plane normal is set to point in the direction of the +z axis (away from the object). Finally, the MST is traversed in depth first order. During traversal, each tangent plane normal is set to point in a direction that is consistent with its parent node’s tangent plane normal in the MST; see Figure 9.
3.4. Computing Signed Distances
For the next stage of Hoppe, et al.’s algorithm, it is necessary to find the signed distance d from a point p to the closest point on the unknown surface M. Since M is unknown, the solution the authors came up with to obtain d is to use the tangent plane with center closest to p as an approximation to the distance to the unknown surface M. The signed distance is positive if p is in front of the tangent plane, zero if p is on the tangent plane, and negative if p is behind the tangent plane. Let D be the distance between p and the closest tangent plane center. The signed
distance d is considered to be undefined if D >= ρ + δ.
In pseudocode, the signed distance calculation looks like this:
find index of closest tangent plane center oi
compute projection z of p onto tangent plane if (D < ρ + δ)
d ← ± || p – z ||
else
d ← undefined end if
3.5. Contouring the Surface
Just as two-dimensional meteorological and topographic datasets can be contoured as 1D curves in R2, three-dimensional datasets can be contoured as surfaces in R3 (Figure 10 and Figure 11). The marching cubes algorithm (Lorensen and Cline, 1987 [9] ) is used to contour 3D datasets as surfaces in R3. In the Hoppe, et al. method, a 3D grid of cubes is superimposed on the sampled dataset (Figure 12). The cube size is determined by the value of ρ + δ. Cube vertices are plugged into the signed distance code to obtain a signed distance at each vertex. The resultant grid of signed distances is contoured using the Marching Cubes algorithm as shown in Figure 13. As an optimization, cubes that do not intersect the surface are not considered.
3.6. Comparison with Original
Figure 14 and Figure 15 show the original and reconstructed surfaces, respectively. The approximation is reasonable with the exception of a rounding-out of sharp edges.

Figure 11. 3D contours [http://www.exaflop.org/docs/marchcubes/ind.html].
3.7. Complexity
The complexity of Hoppe et al.’s algorithm can be summed up as follows:
• EMST graph: O(n2).
• K-neighborhood: O(n + klogn).
• Nearest tangent plane: O(n).
• Construct Riemannian graph: O(nk).
• MST of Riemannian graph: O(nlogn).
• MST traversal: O(n).
• Contouring: O(v), where v is the number of cubes visited.
4. Amenta et al.’s Crust Algorithm
The Crust algorithm of Amenta et al. (1998 [3] ) leverages the concept of the medial axis to help constraint a 3 D
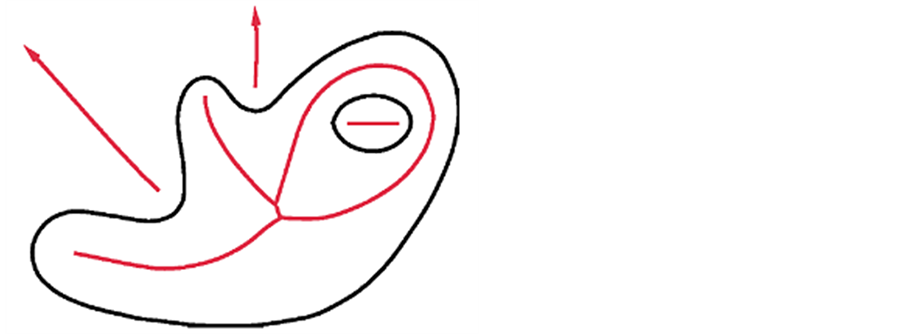
Delaunay triangulation of the sample data to contain the unknown surface. The medial axis is defined to be the locus of points that have more than one closest point on the curve (2D) or surface (3D) (see Figure 16 and Figure 17).
4.1. The 2D Crust Algorithm
Here is the two-dimensional crust algorithm (Figure 18):
1) Compute the Voronoi diagram of the sample points in two dimensions.
2) Construct the Delaunay Triangulation of the sample points plus the Voronoi vertices in two dimensions.
3) The 2D crust (reconstructed curve) is formed by extracting all edges that connect two sample points within the triangulation obtained in Step 2.
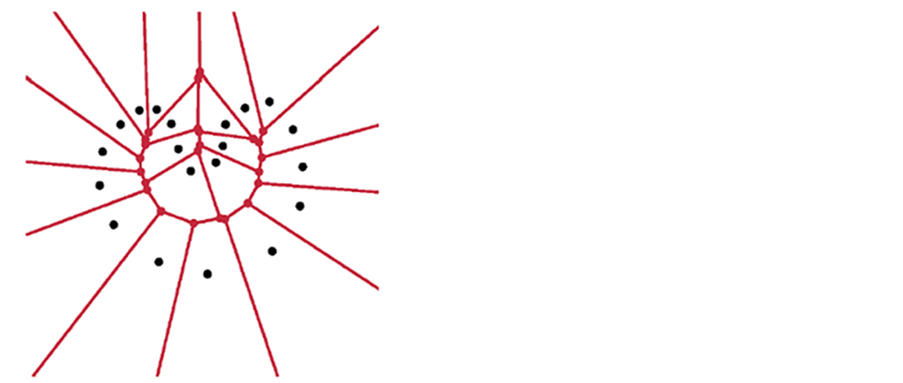
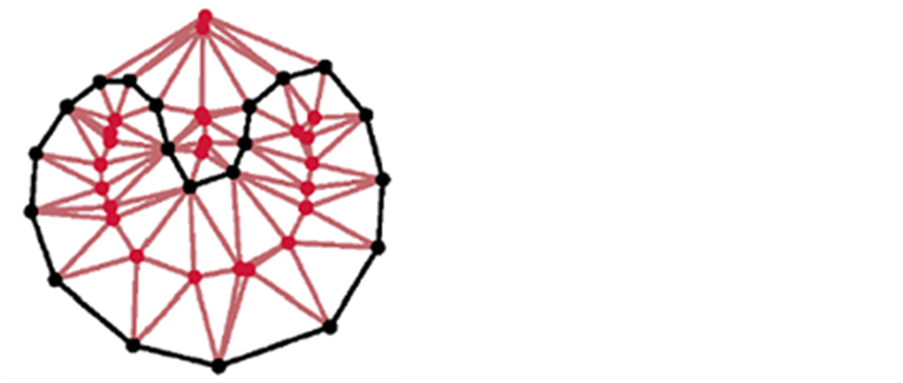
Figure 18. Illustration of the 2D Crust algorithm (Amenta et al., 1998 [3] ). In both diagrams, Voronoi vertices are shown in red and sample points are drawn in black. In the Voronoi diagram shown on the top, it is clear that the Voronoi vertices approximate the medial axis of the curve represented by the sample points. The 2D crust is shown in black in the Delaunay triangulation on the bottom.
In two dimensions, the Voronoi vertices approximate the medial axis. Adding the Voronoi vertices tends to break edges connecting non-adjacent sample points. This will always be true for a sufficiently sampled dataset. The authors call the process of removing edges between non-adjacent sample points Voronoi filtering.
4.2. Obtaining the Sample Point Poles for Use in the 3D Crust Algorithm
The 2D Crust algorithm can be extended to 3D with some modifications. The main difficulty in extending the algorithm is that in three dimensions, the Voronoi vertices don’t necessarily lie close to the medial axis. Fortunately, even though Voronoi vertices aren’t guaranteed to be close to the medial axis, many are. In the 3D Voronoi filtering step, instead of using all Voronoi vertices, the authors use the two Voronoi vertices that are furthest from each sample point s on opposite sides of the unknown surface. They call these vertices the poles of the sample point (see Figure 19).
The sample point poles are obtained as illustrated in Figure 20 in two steps:
1) Find the Voronoi vertex that is furthest from the sample point s. This vertex is the positive pole, denoted p+.
2) Find the Voronoi vertex furthest from s such that the dot product of sp+ and sp− is negative. This ensures that the poles are on opposite sides of the surface.
4.3. The 3D Crust Algorithm
The 3D Crust algorithm can be described as follows:
1) Compute the Voronoi diagram of the sample points in three dimensions.
2) Construct the Delaunay triangulation of the sample points plus the sample point poles (all p+ and p−) in three dimensions.
3) The 3D crust (reconstructed surface) is formed by extracting all triangles that connect three sample points within the triangulation obtained in Step 2.
An example of the 3D crust of a set of sample points extracted from a synthetic surface is shown in Figure 21.
4.4. Post-Processing
There are two separate stages of post-processing: normal filtering and sharp edge filtering. Normal filtering

Figure 19. Sample point poles. In this diagram, the poles are marked as p+ and p−. (Amenta, et al., 1998 [3] ).
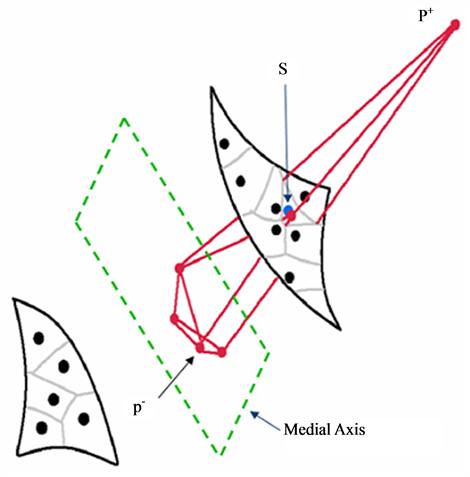
Figure 20. Obtaining the Poles. The sample point is colored blue and is denoted as s. (Amenta, et al., 1998 [3] ).

Figure 21. Crust of sample points de rived from a synthetic surface. Poles are shown in white. (Amenta, et al., 1998 [3] ).
attempts to remove invalid triangles such as those depicted in Figure 22. Since the sample poles tend to be perpendicular to the surface, triangles with normal values that differ too much from the vector between the poles p+ and p− are likely to be incorrect (not parallel to the surface) and are therefore removed.
If it is known that the surface being reconstructed is smooth, then triangles forming sharp edges can be safely removed. Adjacent triangles that form an angle of less than 90 degrees are considered to be part of a sharp edge and are removed by the algorithm. If the surface is not known to be smooth, then sharp edge filtering can not be applied. The Crust surface reconstruction algorithm does not work well when the surface being reconstructed contains sharp edges. The authors experimented with different ways of choosing the poles and were able to improve reconstructions of surfaces with sharp edges.

Figure 22. Invalid triangles that normal filtering attempts to remove. See the detail area within the red dashed circle. (Modified from Amenta, et al., 1998 [3] ).
4.5. Selected Results
Examples of the reconstructed surfaces built by the Amenta, et al. algorithm are shown in Figure 23. The authors offer theoretical guarantees of correctness and convergence provided that certain sampling criteria are met. In practice, however the algorithm occasionally leaves holes or extra invalid triangles in place, in spite of the post-processing efforts described in Section 4.4.
4.6. Complexity
Here is a summary of the complexity of the Amenta, et al. algorithm:
• 2D Delaunay Triangulation: O(nlgn).
• 3D Delaunay Triangulation: O(n2) in the worst case; usually O(n) in practice (input-sensitive).
• Voronoi Diagram: The Voronoi vertices are obtained from the Delaunay triangulation, so the running time is the same as for Delaunay triangulation.
• All other steps: O(n).
5. Summary and Conclusions
There are many applications for surface reconstruction; few were mentioned in the abstract and others could include:
• Surfaces generated from digital scans of real-world objects can be used as computer models in computer aided design (CAD) (Bernardini, et al., 1999 [1] ).
• Medical data can be segmented by hand-digitizing regions or structures of interest in medical datasets. The data may consist of slices through biological specimens (Hoppe, et al., 1992 [2] ), or possibly slices through 3D MRI or CT datasets. The digitized points can be reconstructed into surfaces that correspond to actual surfaces in the sampled specimen.
• In the discipline of geophysics, 3D seismic datasets are often sliced and then hand-digitized along geological boundaries of interest. As with medical datasets, digitized points can be reconstructed into surfaces representing real-world geological structures.
Although many surface reconstruction algorithms are available, this subject is still the focus of much current research. We discussed several different surface reconstruction algorithms in this paper, and we gave special attention to two important ones; the methods of Hoppe, et al. (1992 [2] ) and Amenta, et al. (1998 [3] ). The remainder of this section is devoted to a comparison of relative advantages and disadvantages between these two approaches.
• 5.1. Zero-Set (Hoppe, et al., 1992 [2]) vs. Crust (Amenta, et al., 1998 [3])
• Both algorithms consider the general case of unorganized sets of data points with no additional information.
• The algorithms take completely different approaches to solving the same problem.
• Both algorithms perform better when the sampling density is higher.
• In practice, both algorithms do a reasonably good job of reconstructing the unknown surface.
• 5.2. Zero-Set: Advantages
• The output surface is guaranteed to be continuous with no holes or stray triangles.
• The running time of the algorithm is not dependent on the order of the input points.
• Seems to be faster in practice.
• Approximates the sample points (advantageous with noisy datasets).
• 5.3. Zero-Set: Disadvantages
• Sharp edges are not handled properly—they tend to be rounded in the output surface.
• No provable guarantees of convergence or that the output surface will correctly approximate the input surface.
• You need to specify information about the sampling process (δ and ρ).
• Approximates the sample points (disadvantageous with low-noise datasets).
• 5.4. Crust: Advantages
• Guaranteed to converge to a surface that correctly reconstructs (interpolates) the original unknown surface, provided that strict requirements of sampling density and smoothness are met.
• You don’t need to specify information about the sampling process.
• Interpolates the input points (advantageous with low-noise datasets).
• 5.5. Crust: Disadvantages
• If the sample density requirement is not met, the output surface may contain holes and/or stray triangles.
• The algorithm has trouble with sharp edges.
• The running time of the algorithm is dependent on the order of the input points.
• Seems to be slower in practice.
• Interpolates the input points (disadvantageous with noisy datasets).
Acknowledgements
This research was supported by Yarmouk University, Jordan.
References
- Bernardini, F., Bajaj, C., Chen, J. and Schikore, D. (1999,) Automatic Reconstruction of 3D CAD Models from Digital Scans. International Journal of Computational Geometry Applications, 9, 327-370.
- Hoppe, H., DeRose, T. and Duchamp, T. (1992) Surface Reconstruction from Unorganized Points. Proceedings of ACM SIGGRAPH’92, 27-31 July 1992, Chicago, 71-78.
- Amenta, N., Bern, M. and Kamvysselis, M. (1998) A New Voronoi-Based Surface Reconstruction Algrorithm. Proceedings of ACM SIGGRAPH’98, 19-24 July 1998, Orlando, 415-422.
- O’Rourke, J. (1998) Computational Geometry in C. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511804120
- de Berg, M., van Kreveld, M., Overmars, M. and Schwarzkopf, O. (1997) Computational Geometry: Algorithms and Applications. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-03427-9
- Crossno, P.J. and Angel, E.S. (1999) Spiraling Edge: Fast Surface Reconstruction from Partially Organized Sample Points. IEEE Visualization’99, 24-29 October 1999, San Francisco, 317-324. http://dx.doi.org/10.1109/VISUAL.1999.809903
- Boissonnat, J.-D. (1984) Geometric Structures for Three-Dimensional Shape Representation. ACM Transactions on Graphics, 3, 266-286. http://dx.doi.org/10.1145/357346.357349
- Bentley, J.L. and Friedman, J.H. (1979) Data Structures for Range Searching. Computing Surveys, 111, 398-409.
- Lorensen, W.E. and Cline, H. E. (1987) Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Computer Graphics, 21, 163-169. http://dx.doi.org/10.1145/37402.37422
- Boissonnat, J.-D. and Cazals, F. (2000) Smooth Shape Reconstruction via Natural Neighbor Interpolation of Distance Functions. ACM Symposium on Computational Geometry, 12-14 June 2000, Hong Kong, 223-232.
- Carr, J.C., Beatson, R.K., Cherrie, J.B., Mitchell, T.J., Fright, W.R., McCallum, B.C. and Evans, T.R. (2001) Reconstruction and Representation of 3D Objects with Radial Basis Functions. Proceedings of ACM SIGGRAPH’01, 12-17 August 2001, Los Angeles, 67-76.