Journal of Signal and Information Processing
Vol. 3 No. 1 (2012) , Article ID: 17604 , 15 pages DOI:10.4236/jsip.2012.31001
A Multiresolution Channel Decomposition for H.264/AVC Unequal Error Protection
![]()
Département Génie Electrique, Ecole Mohammadia des Ingenieurs, Rabat, Morocco.
Email: rabbadi@gmail.com
Received October 3rd, 2011; revised November 17th, 2011; accepted November 30th, 2011
Keywords: Multiresolution; H.264/AVC; UEP; PCCC; Turbo Code
ABSTRACT
The most commonly used transmission channel in nowadays provides the same level of protection for all the information symbols. As the level of protection should be adequate to the importance of the information set, it is justified to use UEP channels in order to protect information of variable importance. Multiresolution channel decomposition has emerged as a strong concept and when combined with H.264/AVC layered multiresolution source it leads to outstanding results especially for mobile TV applications. Our approach is a double multiresolution scheme with embedded constellation modulations on its baseband channels followed by OFDM time/frequency multiresolution passband modulation. The aim is to protect The NAL units carrying the most valuable information by the coarse constellations into coarse sub-channels, and the NAL units that contain residual data by fined constellations and transposed into the fined OFDM sub-channels. In the multiresolution protection coding, our approach is a multiresolution decomposition of the core convolutional constituent of the PCCC where the NAL units carrying the most valuable information are coded by the rugged coefficient of the multiresolution code and the NAL units that contains residual data are coded by refined less secure coding coefficients.
1. Introduction
While Shannon theory for the separation of source coding from channel coding hold only for point to point communication system [1]. For Multichannel environment Cover [2] have established that the best scenarios are multiresolution or embedded in character. Source can be represented in hierarchical set of resolutions. A “MR transmission” can then be designed to match the multiresolution source to produce an optimal design.
This paper has three sections. First we investigate the VCL and the NAL of the H.264/AVC for a partitioning of data, our aim is to extract the features of VCL and NAL according to their importance.
The first partition carries valuable data, while others contain irrelevant information. The second section deals with the multiresolution OFDM scheme with double multiresolution approach, we present the multiresolution embedded modulation scheme and discuss its layers performances. In the multiresolution time/frequency OFDM we present the multiresolution channel capacity and the multiresolution spectral efficiency then we close this section with simulations over a DVB-H channel deployment.
Unequal error protection coding can be obtained either by using separate coding schemes with distinct error protection capability for each level of protection or by using a single code with UEP capability. Multi rate filter bank have been proposed for error correcting code, multirate filter bank is a good base for understanding multiresolution of PCCC code for the sake of H.264/AVC UEP. In this section we focus on multiresolution PCCC analysis based on the mapping of the space of convolutional code and the filter bank space (i.e. between the finite state machine space (D transform) and the multirate filter bank space (the z transform). PCCC is decomposed in its multiresolution components. We discuss its bound performance and we generaze for the multilevel multiresolution codeword decomposition system, we present a simulation comparison with conventional single resolution Turbo code for H.264/AVC UEP application.
2. Data Partitioning Structure in H.264/AVC
2.1. Partitioning in the VCL Structure
Since the standardization effort (JVT) has introduced the H.264/AVC and it two layers structure VCL and NAL [3], many features have been added, while others have been withdrawn, but what is striking is its data partitioning as a resilient tool for the VCL layer, however no partitioning has been defined for the NAL. Some structures like error concealment take advantage from this feature while others like Flexible ordering contradict.
2.1.1. Data Partitioning
Data petitioning consists of 3 partitions types A, B, C. it enables unequal error protection depending on syntax elements.
DP A: contains header information including MB types, quantization parameters, and motion vectors MV’s which are more important than any other slice data because without it data on other partition are useless.
DP B: contains intra coded block patterns (CPBs) and intra-transforms coefficients of I-blocks used for reference, the B partition requires the presence of the A partition for a slice to be useful. But the loss of the B partition impairs recovery of successive frames because of error propagation.
DP C: contains inter CBPs and inter-coefficients of Pblocks, it is the biggest in term of number of frame, and its importance is less compared to DP A and DP B.
2.1.2. Error Concealment
Error concealment is performed by the decoder and it concept is based on the fact that corrupted packets are simply discarded and the lost block of video is simply concealed. The error concealment can be grouped in two types: intra-frame interpolation and inter-frame interpolation For inter-frame interpolation, the recovery of lost MVs (partition A) is critical. If and MV is missed it can be calculated based on the motion vectors of the surrounding regions. The error concealment is calculated based on a certain a priori knowledge of the video content. Table 1 shows the recommended action when a partition loss is detected [4].
2.1.3. Flexible Macro Blocks Ordering (FMO)
Flexible ordering of macro blocks allow scattering of possible error so that error accumulation in a limited region of the image is very slim, error concealment is easily performed compared to errors concentrated in a small region [5]. FMO is active only in the base and extended profile, it can fool the data partitioning, and should be idled when data partitioning is active.
2.1.4. Parameter Sets
The parameter set are crucial information sent ahead in an out-of-band channel for extra protection. They are non video data used in the VCL to synchronize with the encoder in terms of syntax and packets, the parameter sets are information about picture size, entropy coding method, motion vector resolution and other relevant coding

Table 1. Recommaded actions when partition loss is detected.
information about a frame or a group of frames.
2.2. Partitioning in the NAL Structure
The network abstraction layer (NAL) formats the VCL data and add the necessary header information for various transport protocol, data such as picture slices and parameter set are sent from the VCL to the NAL and encapsulated into NAL units.
NAL units can be categorized in two types:
• VCL NAL units: These NAL units contain data that represents the values of the samples in the video pictures.
• Non-VCL NAL units: These NAL units contain any associated additional information such as parameter sets and supplemental enhancement information.
The NAL header consists of one forbidden bit; two bits (nal-ref-idc) indicating whether or not the NAL unit is used for prediction, and five bits (nal-unit-type) to indicate the type of the NAL unit [6].
Nal-unit-type 1 - 5 and 12 are video data (picture slices) called VCL NAL units. The rest of the nal-unittypes are called non-VCL NAL units and contain information such as parameter set and supplemental information. Of these NAL units, IDR pictures, SPS, and PPS are the most important.
A sequence parameter set (SPS) contains important header information that applies to all NAL units in the coded video sequence. A picture parameter set (PPS) contains header information that applies to the decoding of one or more pictures within the coded video sequence.
An IDR picture refreshed all the information which indicates a new coded video sequence.
Similar to data partitioning (DP) in the VCL layer where the most important video data (headers, MVs and addressing data) are ahead of the non-important data, NAL can be partitioned into two parts: the first partition contains the most important unit type of the streamed NAL data (such as unit type 1, unit type 2, IDR and most importantly the SPS and PPS) ahead of the second partition which contain no relevant data. Our scheme focuses on the following four NAL unit types: coded slice, IDRSPS and PPS, since video sequences are composed mainly of these type. Figure 1 shows an example of a bit stream and the relationship between the parameter sets and slices as mentioned before. It is readily seen that theses NAL units have higher priority.
In a stream, there are three possible permutation of how NAL unit groups can be formed (Figure 2). Permutation S always appears at the beginning, an SPS, PPS, and IDR are followed by coded slices. This permutation has very high priority level. Permutation P appears when the PPS are updated and is of lower priority, permutation C appears the most frequently and consist only of coded slices.
3. The Multiresolution OFDM System
Multiresolution is a strong concept when combined with UEP leads to excellent results, In OFDM multi-resolution concept one can differentiates between the multi-resolution modulation in which embedded modulation is used and time-frequency multiresolution in which the frequency tones or filters of the MR OFDM are modulating symbols of unequal duration in a manner that optimize the performance of the overall system. Wavelets have been used for this end.
3.1. Multiresolution Modulation
3.1.1. Embedded Multiresolution
In theory [7], it has been shown that a 16-QAM signal embed two QPSK signals, in the same way, we show that a 64-QAM embed either a 3 QPSK signals, or a QPSK signal plus a 16-QAM signal. Each complex modulated symbol xn is chosen from a 64-QAM constellation that can be expressed as:
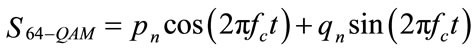
where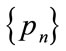 ,
, 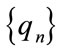 take the elements from the set
take the elements from the set 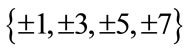
A 16-QAM constellation can be realized as the sum of two QPSK signals:
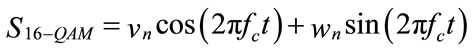
where 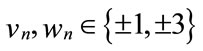
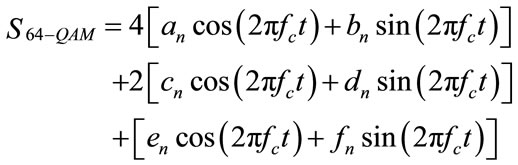
where 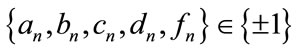
That is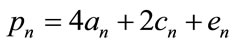 ,
,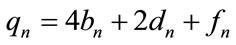 .
.
Thus a 64-QAM can be realized as the sum of three QPSK, or as the sum of a QPSK and a 16-QAM constellation.
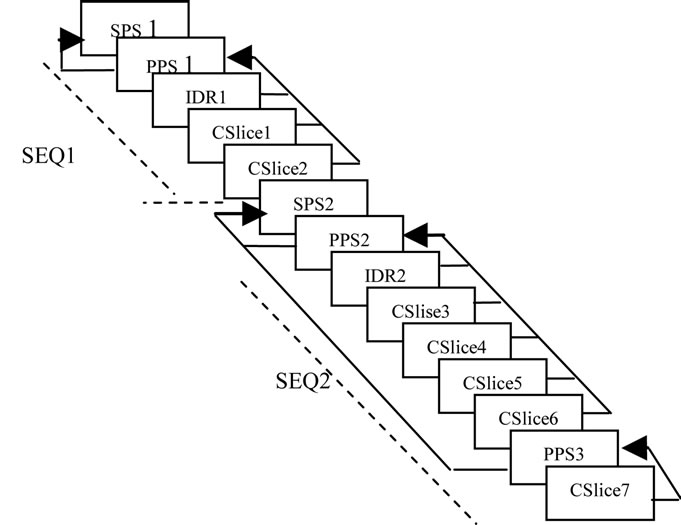
Figure 1. NAL relationship between SPS, PPS, IDR, and coded slice in a bitstream.
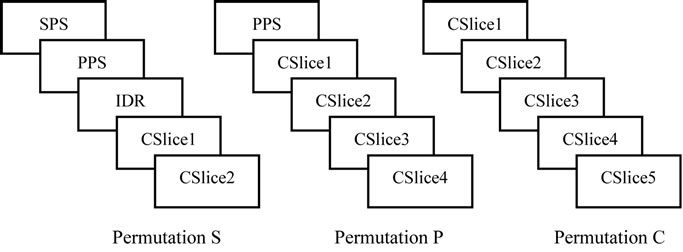
Figure 2. NAL unit group permutations in a bitstream.
More generally, if we consider that a QPSK constellation can be realized as  where
where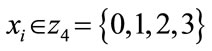 , then an M-QAM constellation
, then an M-QAM constellation 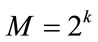 is:
is:
For n an even number:
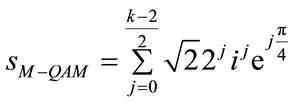
For odd number:
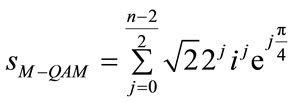
The main idea of the multiresolution is to group a constellation’s points in a non-uniform way in order to create sub-constellations which may be grouped into others sub constellations, each level has a degree of ruggedness, it is a combination of the embedded and hierarchical modulation concepts. In the MR 64-QAM, the constellations points have been grouped in four groups (or clouds), each with sixteen points (satellites), thus generating 16- QAM sub-constellations. The 64-QAM constellation can be seen as a 16-QAM embedded into a QPSK modulation, where the coarse (HPS) coefficients are represented by each cloud (or quadrant) and the fine coefficients (LPS) are associated by the points (satellites).
The ratio of the protection degree between the two coefficients (HPS and LPS) is determined by the parameter
 , it is the ratio between the intercloud (coarse)
, it is the ratio between the intercloud (coarse)
d2 and the intra-cloud (fine)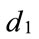 ,
, 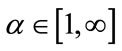
If 
with increasing value of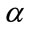 , the ruggedness difference between the HPS and the LPS is also increased. The constellation vector
, the ruggedness difference between the HPS and the LPS is also increased. The constellation vector  depend on
depend on 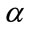 and M and is given by:
and M and is given by:
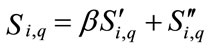 which is a linear combination of the two modulations where:
which is a linear combination of the two modulations where:
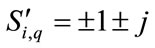 represents the constellation vectors generated by the HPS sequences (coarse).
represents the constellation vectors generated by the HPS sequences (coarse).
 represents the constellation vector generated by the LPS sequence (fine).
represents the constellation vector generated by the LPS sequence (fine).
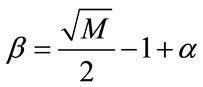 is the constellation expansion factor associated to the HPS sequence.
is the constellation expansion factor associated to the HPS sequence.
3.1.2. Multiresolution Code Design
To design a MR constellation system involve finding non-uniform sequence of amplitudes 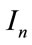 [8]. Consider two data streams (Coarse and Fine) having different BER requirement. Take two bits from coarse stream and two bits from fine stream, using them make an amplitude level
[8]. Consider two data streams (Coarse and Fine) having different BER requirement. Take two bits from coarse stream and two bits from fine stream, using them make an amplitude level  which can take 4 possible values.
which can take 4 possible values.
In a 16-QAM constellation I = –3, –1, 1, 3, results in differences x = ±2, ± 4,± 6, (k = {1,2,3}), which are equally spaced. To achieve multiresolution, we need to introduce unequally spaced points as shown in Figure 3, I would be in the set {–2 – b, –2 + b, 2 – b, 2 + b}. (Note that for, b = 1, we have the SR case.) This results differences:
x = ±2b, ±2(2 – b), ±4, ±2(2 + b), resulting in k varying over {b, 2 – b, 2, 2 + b}. In general, for M-array signals, k varies in the set 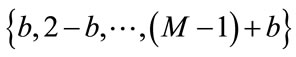 which results in M – 1 unique distances between signal symbols.
which results in M – 1 unique distances between signal symbols.
The codebook design is then based two concepts:
1) First Group the points, so that intra-group Euclidean distance is less than inter-group Euclidean distance
2) Second map the points according to the Gray code fine-channel digital bit mapping
a) Arrange the euclidean distances di in increasing order. Each di corresponds to a Di.
b) Three groups are possible for coarse codebook, as shown in Figure 4. In a group, the intra-group distance must be chosen the minimum one. For coarse data error probability, intra-group Euclidean distance does not matter. Note that possible intra-group distances for M = 4 cases are {(d1, d1), (d2, d4), (d3, d3)}.
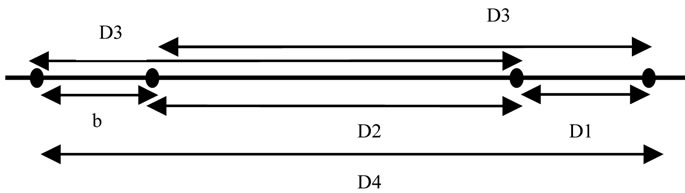
Figure 3. Unique distances in a MR 16 QAM signal.

Figure 4. Three coarse codebooks for MR-16-QAM. For each codebook, coarse information is represented by closed circle.
c) For each coarse codebook, two fine codebooks are possible. They are chosen on the basis that the points with second smallest distance from each other.
The Codebook for two-layered MR-16-QAM data with two bits in each layer is given in Table 2:
3.1.3. Performance of MR-MQAM
The OFDM MR-modulation have the desirable property that the probability of the symbol error of the coarse layer is unaffected by the error in the fine layers. The high profile base layer video source stream is modulated onto OFDM-carriers using Gray-coded QPSK modulation, every two binary symbols are mapped into one QPSK symbol, the QPSK signaling constellation is then converted to a non-uniform 16-QAM signal constellation by splitting each point in the QPSK constellation into four points, each of which is rotated away from the original QPSK point by an angle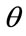 , as illustrated in Figure 5. The result is a non-uniform 16-QAM signal constellation with signal at angles in the first quadrant at
, as illustrated in Figure 5. The result is a non-uniform 16-QAM signal constellation with signal at angles in the first quadrant at  each point of the 16-QAM is split into four points, each of which is rotated by the same amount
each point of the 16-QAM is split into four points, each of which is rotated by the same amount 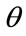 from the 16-QAM points.
from the 16-QAM points.
The high profile base layer data (coarse) is represented by the pairs of binary symbols which appear as the first two bits of the labels of the points in the 16-QAM constellation. The last two bits of each label are derived from

Table 2. Code book for two-layered data with two bits in each layer. First bits represent coarse data.
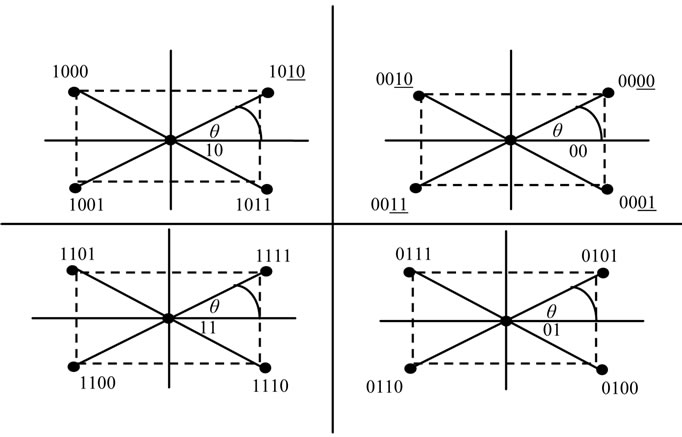
Figure 5. Signal constellation for MR 16-QAM.
the enhanced layer data (fine data). The relative probability of the error for the two message streams are controlled by varying the modulation parameter 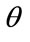 from
from
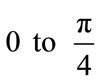 called also the offset angle. To derive the error probability for data mapping to different resolutions of the signal constellation, we have followed [9]. The noise is modeled as stationary Gaussian noise with one sided spectral density
called also the offset angle. To derive the error probability for data mapping to different resolutions of the signal constellation, we have followed [9]. The noise is modeled as stationary Gaussian noise with one sided spectral density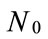 . If
. If  is the symbol energy for PSK, then
is the symbol energy for PSK, then 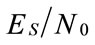 determines the symbol error probability. The error bounded for uniform QPSK, 4-QAM, 16-QAM and 64-QAM constellation are special case with
determines the symbol error probability. The error bounded for uniform QPSK, 4-QAM, 16-QAM and 64-QAM constellation are special case with . For a fixed value of
. For a fixed value of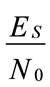 , the probability of bit error for the coarse layer increases while the probability of the fine layer decreasethe offset angle
, the probability of bit error for the coarse layer increases while the probability of the fine layer decreasethe offset angle 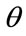 is increased form
is increased form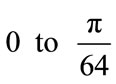 . The symbol error region for the coarse layer (basic message) for 16-QAM lies in the first quadrant. The boundaries for decision region are
. The symbol error region for the coarse layer (basic message) for 16-QAM lies in the first quadrant. The boundaries for decision region are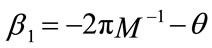 , and
, and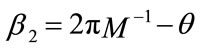 . Following [9], the probability of symbol error is:
. Following [9], the probability of symbol error is: 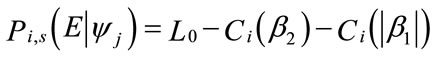
The bit error probability for the high profile coarse layer for M-QAM is approximated by:
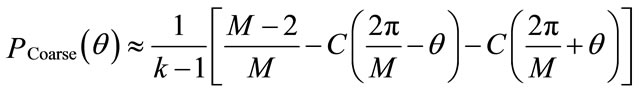 (1)
(1)
where:

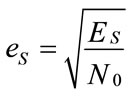 ,
, 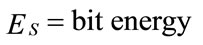
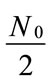 : Two sided power spectral density of the stationary AWGN
: Two sided power spectral density of the stationary AWGN
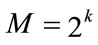 , and
, and 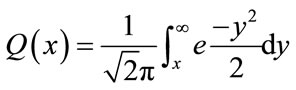
For the enhanced fine layer the upper bound for the probability of bit error is given by:
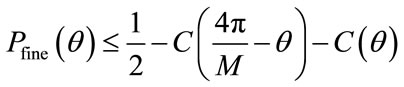 (2)
(2)
3.1.3.1. Probability of Error of 2 Layers 4-QAM:
The probability of error of 4-QAM can be determined by analyzing the signal in term of in-phase and quadrate component, the probability of error of the low resolution coarse layer according to Equation (1) is:
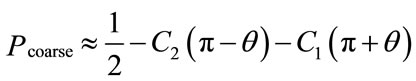
Which simplify to: 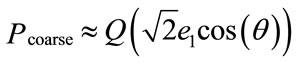 for M = 4, for the high resolution layer, the probability of error is according to Equation (2)
for M = 4, for the high resolution layer, the probability of error is according to Equation (2)
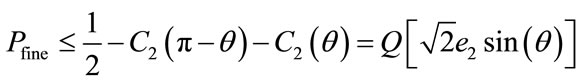
3.1.3.2. Probability of Error of 2 Layers 16-QAM
A 16-QAM constellation can be see as a two layer multiresolution constellation of two QPSK constellations (Figure 5), using the Equation (1) , the probability of the coarse base –layer of the nth channel for the 16-QAM is given by:

We use the fact that
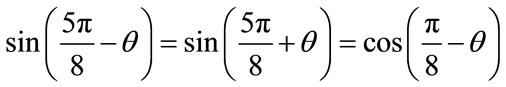
And 
And
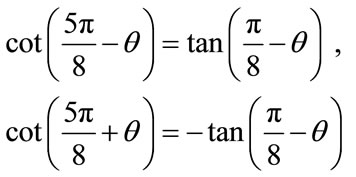
And 
which yield :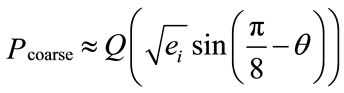 .
.
This is the probability of the 4-PSK signal constellation.
The probability of error for the fine additional message is according to (2):
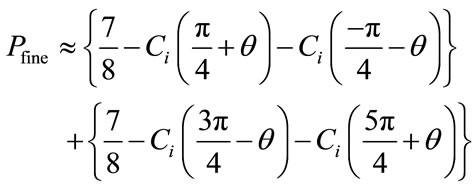
3.1.3.3. Probability of Error of 2 Layers 64-QAM
A 64-QAM constellation can be see as a two layer multiresolution constellation of a coarse QPSK constellation, and a 16-QAM fine constellation (Figure 6), or as a three layers multiresolution constellation of three QPSK modulations. In the case of two layers multiresolution, and using the Equation (1), the probability of the base coarse layer is:
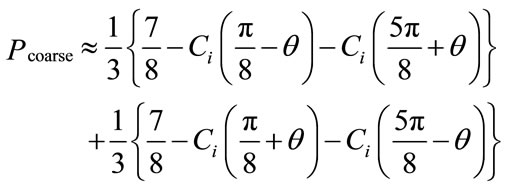
The probability of error for the fine additional message is according to Equation (2) is:
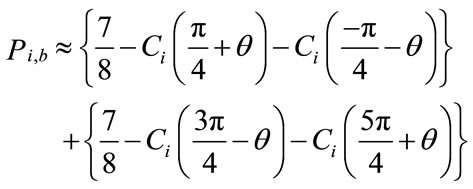
3.2. OFDM Time-Frequency Multiresolution
The general principal of OFDM system is to achieve high speed data throughput by using multiple orthogonal carriers for the transmission of data. There are a number of ways by which the OFDM system can be implemented. Fourier OFDM is one of them, but multiresolution OFDM have recently emerged especially wavelet as an interesting OFDM system.
In Fourier OFDM, symbol consists of N subcarriers separated by a frequency distance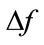 . The total system bandwidth B is divided into N equidistant sub channels with all subcarriers being mutually orthogonal within a time interval
. The total system bandwidth B is divided into N equidistant sub channels with all subcarriers being mutually orthogonal within a time interval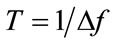 . The OFDM signal in the time domain is
. The OFDM signal in the time domain is
 (3)
(3)
To obtain the discrete time representation, the signal x(t) has to be sampled. The sampling time needs to be twice the bandwidth that is 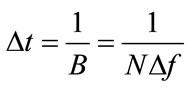 so that the
so that the

Figure 6. Signal constellation for MR 64-QAM.
signal can be recovered, the sampled signal is given by:
 (4)
(4)
Equation (3) represents an N point inverse discrete Fourier transform (IDFT) of the input symbols . These inputs symbols
. These inputs symbols 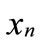 represent digitally modulated complex data. The IDFT can be implemented using the inverse fast Fourier transform (IFFT) algorithm. The representation time/frequency is depicted in Figure 7(a).
represent digitally modulated complex data. The IDFT can be implemented using the inverse fast Fourier transform (IFFT) algorithm. The representation time/frequency is depicted in Figure 7(a).
In the multiresolution (wavelets) OFDM system, the IFDT and the FDT are replaced by the IDWT and the DWT. The main advantage of wavelet OFDM over Fourier OFDM is the use of the time-frequency multiresolution.
There are two general approaches to implement OFDM wavelet transforms [10]. The first is denoted as classical wavelet. The second method uses full decomposition and recomposition trees, and is called Wavelet Packet.
In the classical wavelet analysis the signal is coded using a recomposition tree. The transmitter first splits the data sequence, filters each of the subsequences to create the resulting OFDM symbol. The OFDM sequences are then processed in a serial fashion for transmission. This approach leads to the time/frequency representation shown in Figure 7(b), where each block represents a single data symbol. Each of these blocks has the same area, but symbols mapped to higher frequencies have shorter time durations. The data rate is adapted to the carrier frequency as symbols occupy different periods of their assigned sub-carriers. One can map the coarse modulated symbol of the MR constellation to coarse coefficients carriers frequencies (i.e. QPSK base layer symbols carrying high profile unit to more rugged carriers where the spectral efficiency is not a concern), and the fined modulated symbol of the MR constellation to fined coefficients carriers (i.e. 16-QAM symbols to the fine carriers frequencies). Multiresolution OFDM wavelet do not need cyclic prefix for synchronization which leads to a better symbol rate.
In the wavelet packet approach, the time/frequency representation leads to the figure shown in Figure 7(c). This approach is not optimal for the multiresolution because the block has the same area.
3.2.1. Spectral Efficiency of Multiresolution OFDM Channels
In most digital communication systems, the available channel bandwidth is limited, one of the most important feature of multiresolution OFDM is it spectral efficiency. It is then important to determine the spectral content of the digitally multiresolution modulation and multiresolution OFDM modulated signal. From theory we know that power spectral density is used to determine the channel bandwidth required. We can then determine the channel efficiency of the multiresolution OFDM.

Figure 7. (a) Single-resolution (Fourier) OFDM symbol; (b) Multiresolution classical wavelet OFDM symbol; (c) Multiresolution packet wavelet OFDM symbol.
Average Energy of MR-OFDM Channel In [11] it has been shown that the average power of a single M-QAM constellation is equal to the average energy of one of the quadrants.
The number of symbols in each of the quadrant is M/4, for each symbol i, the energy 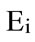 is given in term of its coordinates
is given in term of its coordinates ,
,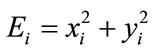 , the average energy is:
, the average energy is:
 the number of symbol in each of the quadrate is:
the number of symbol in each of the quadrate is: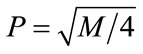 . The symbols have coordinates
. The symbols have coordinates where
where
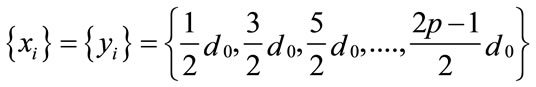 the average energy for a squared constellation is
the average energy for a squared constellation is

For the cross constellation, it has been shown [11] that:
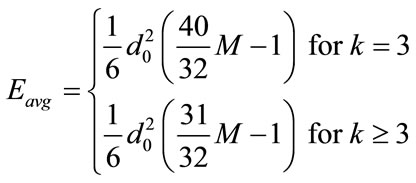
The average energy of the coarse base layer dedicated to the nth sub channels can be determined according to the number of the two bits symbols which are located in the first quadrant. For MR-QAM the average energy of the base layer is:
 (5)
(5)
For the fine enhanced layer the number of additional bits symbols in each quadrant is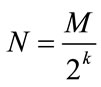 . The average energy for theses fine additional layers dedicated to the mth sub-channels is:
. The average energy for theses fine additional layers dedicated to the mth sub-channels is:
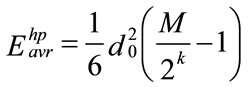 (6)
(6)
The average energy of the MR constellation nth subchannel is then: 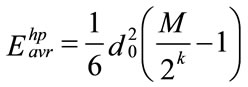
 k even,
k even, 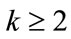
where k is the number of bits which determine the level of multi-resolution in the constellation and the distance  is arbitrary.
is arbitrary.
The total average energy of the MR-QAM is the total energy of the coarse base layer plus the fine enhanced layer which is:
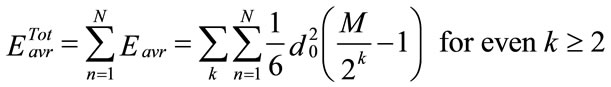
From Equations (5) and (6), we have:
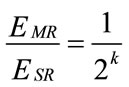 . (7)
. (7)
Note that 
3.2.2. Channel Capacity of MR OFDM Channel
The capacity of the band-limited AWGN MR nth channel is:  Where W is the bandwidth, and
Where W is the bandwidth, and 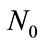 is the energy of the noise, hence:
is the energy of the noise, hence:
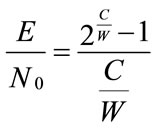 .
.
For the same channel bandwidth W and using Equation (7), we have:
 (8)
(8)
where 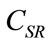 is the capacity of the single resolution constellation. Figure 8 is the plot of Equation (8) for k = 0, 4,
is the capacity of the single resolution constellation. Figure 8 is the plot of Equation (8) for k = 0, 4,
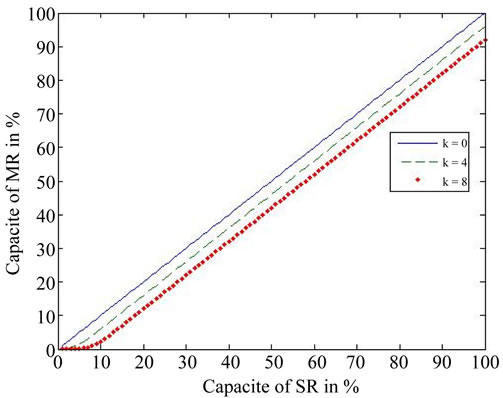
Figure 8. Capacity of MR vs. SR channels.
and 8.
For k = 0, we have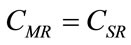 .
.
For k = 8, we have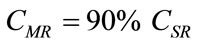 .
.
Spectral Efficiency of MR OFDM Channel According to [12], the band pass filters have the bandwidth:
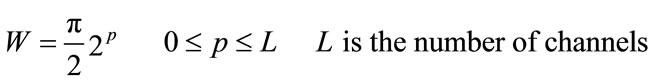 .
.
The efficiency of the bandwidth usage of the nth channel is:
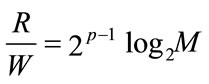 (9)
(9)
where 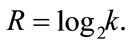
Table 3 shows the spectral efficiency for the single and a multiresolution 16-QAM and 64-QAM. It is twice efficient in the case of a double layer MR 64-QAM, and three times in the 3 layers case.
3.3. Experimental Results and Discussion
In this work, we have focused on the DVB-H 4K mode standard [13] intended for mobile reception of standard definition DTV. First we have classified the NAL unit type into two layers: SPS and PPS as highly prioritized units, their identification in the NAL stream is as follows: From the test. 264 file generated by the JM 11 encoder there is 31104 bits, in which 216 are high priority substream and it consists mainly of NAL unit type 7 which is SPS, and NAL unit type 8 which PPS, JM1l decoder is zero tolerant for these loss of these units, the left substream is treated as low priority, The OFDM system is specified for 8 Mhz channel spacing, the parameters are the same except for the period T, The two independents H264 streams are mapped on to the multi-resolution modulation signal constellations to generate symbols constellations in the baseband channels (Figure 9).
In the pass band domain, the transmitted OFDM signal is organized in frame of duration  and consists of 7771 OFDM symbols. Each OFDM symbol is constituted by a set of K = 3408 carriers in the 4K mode and transmitted with duration Ts, A useful part with duration
and consists of 7771 OFDM symbols. Each OFDM symbol is constituted by a set of K = 3408 carriers in the 4K mode and transmitted with duration Ts, A useful part with duration 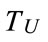 and a guard interval with a duration
and a guard interval with a duration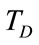 . The subcarrier 1 is 7.61/2 MHz to the left and sub carrier 3408 is 7, 61 to the right. Figure 10 shows the PSD of the 64-
. The subcarrier 1 is 7.61/2 MHz to the left and sub carrier 3408 is 7, 61 to the right. Figure 10 shows the PSD of the 64-
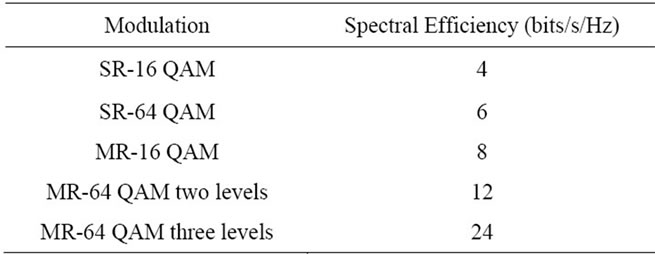
Table 3. Spectral efficiency single vs. multiresoltion OFDM.
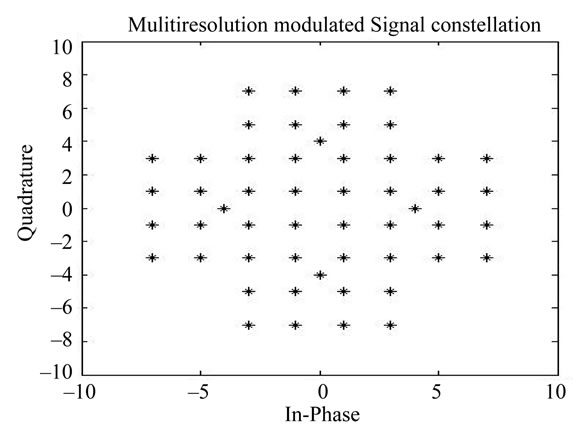
Figure 9. Multiresolution constellation for H.264/AVC file input.

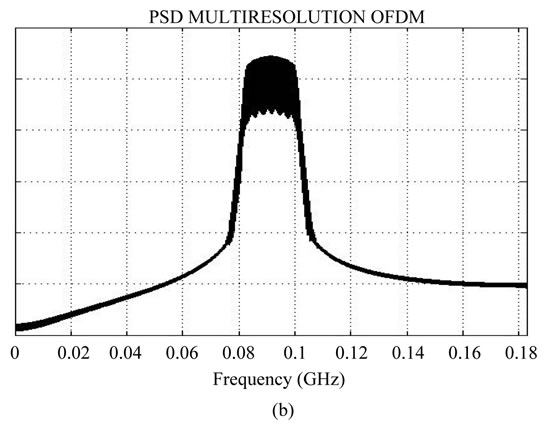
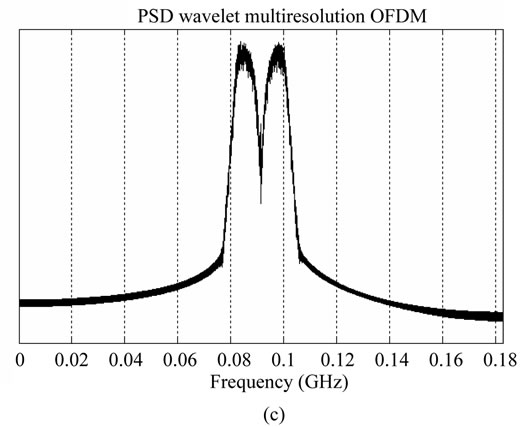
Figure 10. PSD of (a) single; (b) multiresolution 64-QAM modulation OFDM over DVB-H 4K channel and H264 file input; (c) wavelet OFDM.
QAM single and multiresolution modulation for DVB-H 4K mode with layered H264 file input.
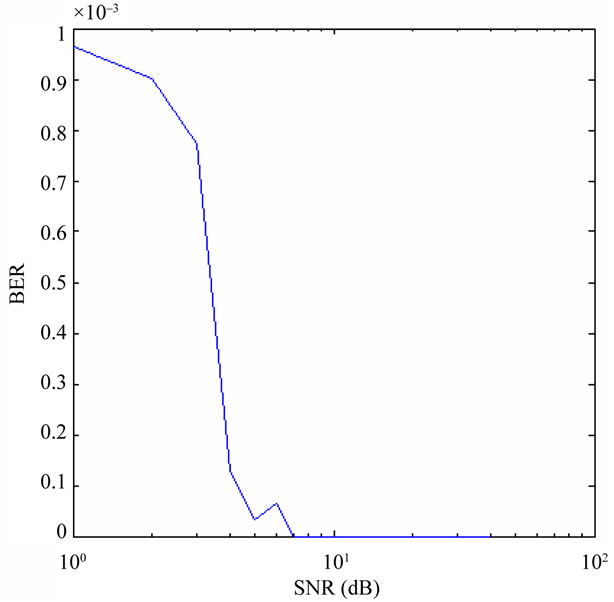
Figure 11(a) is the plot of BER vs. SNR for a two level 64-QAM multiresolution modulation in a SNR environnement, and (b) is the performance of a two level 64-QAM multiresolution modulation in a Raleigh fading environnement.
4. The Multiresolution Turbo Code System
Multiresolution analysis via decomposition is an important tool in signal analysis. An analogous framework for the multiresolution analysis of finite-length sequences from aritrary field was defined in term of the generator matrices of convolutional code [14]. Convolutional codes are core constituent for turbo coding and can be treated using both the multirate analysis because of their convolution property and the finite state machine analysis. In this work we will use both analysis for understanding the behavior of multiresolution and decomposition of convolutional code and hence the PCCC and the Turbo codes.
In theory a coded stream is a convolution of the input stream with encoder’s impulse responses:
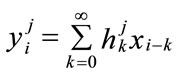
where 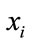 is an input sequence,
is an input sequence, 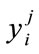 is a sequence from output and
is a sequence from output and 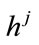 is an impulse response for output j. A convolutional encoder is a discrete linear time-invariant system. Every output of an encoder can be described by its own transfer function, which is closely related to a generator polynomial. The Transfer function for the recursive encoder of Figure 7 used in [15] is:
is an impulse response for output j. A convolutional encoder is a discrete linear time-invariant system. Every output of an encoder can be described by its own transfer function, which is closely related to a generator polynomial. The Transfer function for the recursive encoder of Figure 7 used in [15] is:

Define m as: 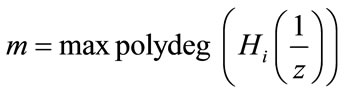 where for any rational function
where for any rational function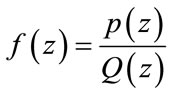 polydeg (f) = max(deg(p),deg(Q))
polydeg (f) = max(deg(p),deg(Q))
Then m is the maximum of the polynomial degree of the 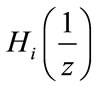 , and the constraint length is defined as: k =
, and the constraint length is defined as: k =
m + 1. The constraint length of the encoder of Figure 12 is 5.
Let the input to the encoder at time K is a bit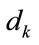 , and the corresponding codeword is the bit pair (
, and the corresponding codeword is the bit pair ( ,
,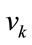 ) where:
) where:

 (a)
(a) (b)
(b)
Figure 11. Plot of BER vs. SNR of multiresolution OFDM. (a) SNR channel; (b) Rayleigh channel.
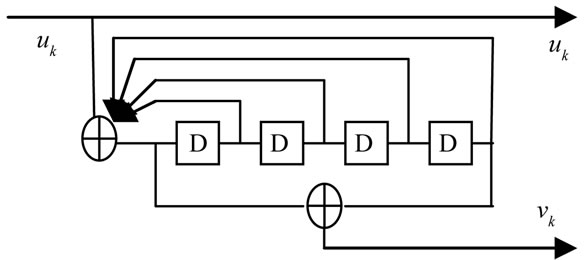
Figure 12. SR [37,21] recursive convolutional code.
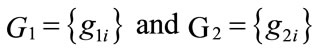 are the code generators, and
are the code generators, and 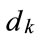 is represented as a binary digit. This encoder can be visualized as a discrete-time finite impulse response (FIR) linear system, and in the case of recursive constituent code; it is equivalent to an infinite impulse response filter (IIR).
is represented as a binary digit. This encoder can be visualized as a discrete-time finite impulse response (FIR) linear system, and in the case of recursive constituent code; it is equivalent to an infinite impulse response filter (IIR).
4.1. Polyphase Decomposition
The polyphase representation has been an important advancement in the mulitrate signal processing, which permits great simplification of theoretical results and alleged complexity [12].
Consider a coder with generator function:
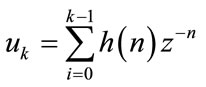
By separating the even numbered coefficients of h(n) from the odd numbered ones, we can write:
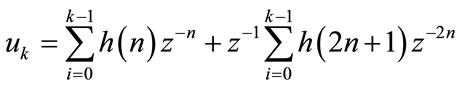
Defining:
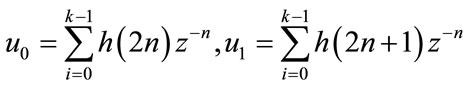
Therefore, we can write: 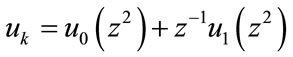
In general, we have:
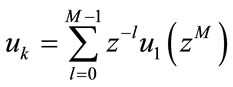 where
where 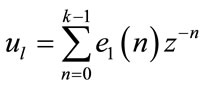
With

the signal y(n) is obtained by interlacing y0(n) and 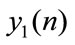 that is,
that is, 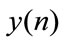 is:
is: 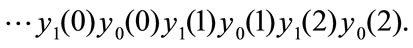
Which is a time-multiplexed version of the output of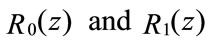 .
.

4.2. Multiresolution Transfer Function
Finding the free distance of a PCCC and therefore of a Turbo code is complicated by the fact that these code are time varying due to the interleaver.
In the case of single resolution, many approaches for the evaluation of the transfer function of the PCCC have been proposed in the literature. The two most famous are those of Disalvar et al. [16] and Benedetto and Montorsi [17,18]. In this paper the methods in [17,18] have been followed.
Let
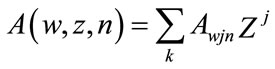

Be the parity-check enumerating function of the sequences of the convolutional code generated by concatenating n error events with total information w.
 is the number of codewords with information bit weight w, parity-check weight j and number of concatenated error n, and Z in the dummy variable.
is the number of codewords with information bit weight w, parity-check weight j and number of concatenated error n, and Z in the dummy variable.
In multiresolution coding, the dummy variable of the high coder is 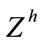 and the low coder is
and the low coder is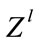 , where h is the high parity-check weight and l is the low parity-check weight by using the property of “Devide and Concert” of polyphase decomposition, we can decompose the convolutinal code to its components, the free distance of the CC is the sum of the free distance of it components.
, where h is the high parity-check weight and l is the low parity-check weight by using the property of “Devide and Concert” of polyphase decomposition, we can decompose the convolutinal code to its components, the free distance of the CC is the sum of the free distance of it components.
The parity-check enumerating function of the sequences of the multiresolution code can be written in matrix form as:
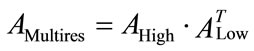
where 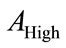 and
and 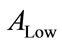 are respectively the enumerating function of the high level component and low level component. The multiresoltion conditional weight enumerating function can be written as:
are respectively the enumerating function of the high level component and low level component. The multiresoltion conditional weight enumerating function can be written as:
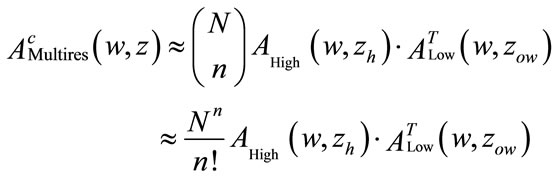
The conditional weight enumerating function of the two  constituent equivalent block of the two PCCC code is defined as:
constituent equivalent block of the two PCCC code is defined as:
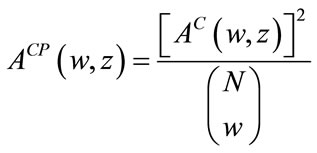
4.3. Multiresoltion Performance Bound
The input sequence is restricted to thengh N, where N correspond to the size of the interleaver of the PCCC. With finite length input sequences of length N. A 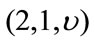 convolutional code may be viewed as a block code with
convolutional code may be viewed as a block code with  codewords of length
codewords of length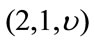 . For the multiresolution case and following [18], we get for the conditional weight enumerating function:
. For the multiresolution case and following [18], we get for the conditional weight enumerating function:
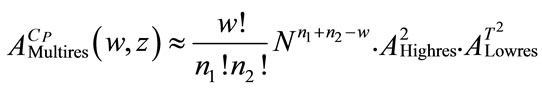
For large N the approximation 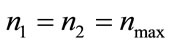 is used and the asymptotic bound for the bit error probability:
is used and the asymptotic bound for the bit error probability:
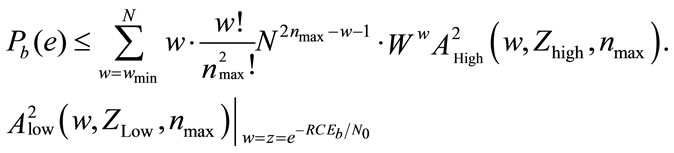
where  denotes the minimum information weight in the error events of the CC.
denotes the minimum information weight in the error events of the CC.
For nonrecursive convolutional constituent encoder, we have  and
and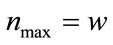 , and
, and 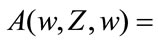
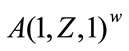 and the asymptotic bound becomes:
and the asymptotic bound becomes:

For the most favorable case (w = 1) the bit error probability is independent of N.
For recursive encoders 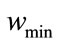 has been shown to be equal to 2 and
has been shown to be equal to 2 and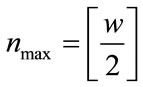 , Using the same approximation as in [18], we have:
, Using the same approximation as in [18], we have:
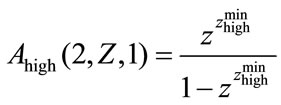 and
and 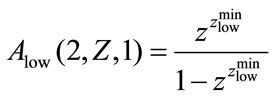
And the asymptotic expression of the upper bound yield to:
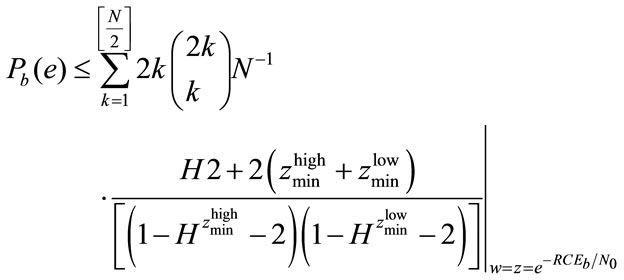
The interleaver gain for the PCCC of the constituent encoders goes as , the interleaver size N can be split in high resolution and low resolution components.
, the interleaver size N can be split in high resolution and low resolution components.
The effective free distance of the multiresolution PCCC can be defined as:
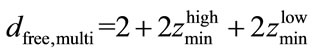
From the above equation we can choose the encoder decomposition so that the free distance 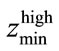 of the high level encoder which protect the sensitive information greater than the free distance of the low level encoder
of the high level encoder which protect the sensitive information greater than the free distance of the low level encoder  which protect the irrelevant information.
which protect the irrelevant information.
Example: Berrou Turbo Code
Consider the turbo code of [15], the generator matrix of the systematic recursive convolutional code [37,21] is:
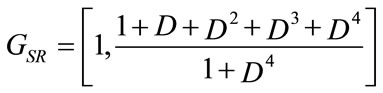
Using the type I polyphase decomposition, we get the generator matrix of the high level constituent encoder [7, 5] (Figure 13):
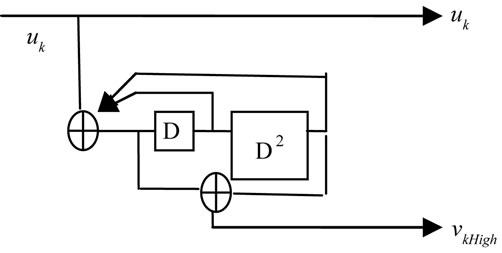
Figure 13. HR [7,5] recursive convolutional component code.
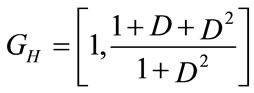 and
and 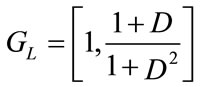 for the low resolution constituent encoder [6,5] (Figure 14), up on solving the state equations for the ratio
for the low resolution constituent encoder [6,5] (Figure 14), up on solving the state equations for the ratio 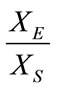 of the augmented state diagrams for the high level and low level encoder, the transfer function for the HR encoder is:
of the augmented state diagrams for the high level and low level encoder, the transfer function for the HR encoder is:
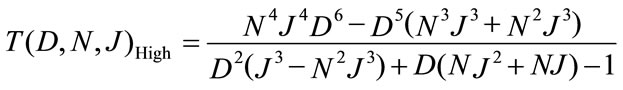
Setting J = 1, the free distance 
And for the transfer function of the LR encoder is:
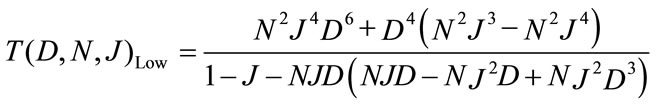
Setting J = 1, the free distance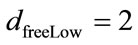 , the free distance of the (37,21) code is therefore equal to 7.
, the free distance of the (37,21) code is therefore equal to 7.
Figure 15 shows the multiresolution state diagram of the (37,21) code where the two output bits are the HR output and the LR output of the multiresolution encoder.
Figure 16 shows the theoretical bound for SR (37,21) Turbo code and its MR (7,5) and (6,5) components.
4.4. Generalisation of Multiresolution Decomposition
The UEP capability of a convolution encoder is measured by the effective free distance vector of length k (the number of possible UEP protection levels). If all entries in the free distance vector are equal, then the encoder possesses the equal error protection (EEP) capability [19].
In theory we consider the codeword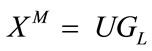 , where
, where 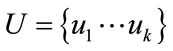 is the input word and
is the input word and  is the codeword, the error vector is defined as:
is the codeword, the error vector is defined as: 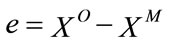 where
where 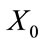 is the distorted codeword.
is the distorted codeword.
If the decoding is done according to free distance, then if the ith symbol is protected against error of class  whereas the j-t symbol is protected against error of class
whereas the j-t symbol is protected against error of class 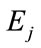 where
where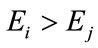 , then the
, then the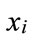 -th symbol can be decoded correctly if
-th symbol can be decoded correctly if 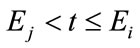 whereas codewords protected by class
whereas codewords protected by class 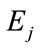 is distorted. In general if
is distorted. In general if  is a set of distortion codeword vector, the magnitude of which is
is a set of distortion codeword vector, the magnitude of which is
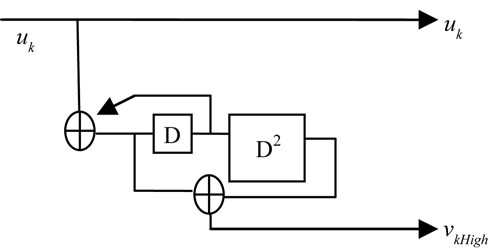
Figure 14. Low R [6,5] recursive convolutional component code.
not higher than , then the i-th symbol of the codeword is protected against
, then the i-th symbol of the codeword is protected against  errors. The structure of concatenating systematic convolutionel code used in PCCC allow the generation of new UEP codes.
errors. The structure of concatenating systematic convolutionel code used in PCCC allow the generation of new UEP codes.
The concatenation of matrices can be used to create new correcting codes; using matrices 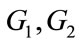 the following matrices are generated:
the following matrices are generated:
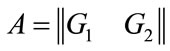 And
And 
It is evident that if 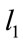 and
and  are linear
are linear 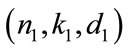 and
and 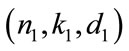 code then the concatenation of type A generate a
code then the concatenation of type A generate a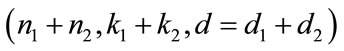 , while the concatenation B will generate a
, while the concatenation B will generate a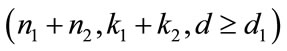 .
.
A particular switch in the rows of 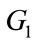 will generate a code which will protect two groups of symbols: the first group by the free distance
will generate a code which will protect two groups of symbols: the first group by the free distance 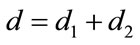 and the second one by
and the second one by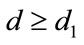 . The matrice
. The matrice 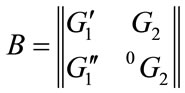 generates a
generates a 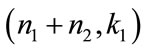 code with the minimum distance d =
code with the minimum distance d = 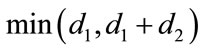 The matrix generated using concatenating has size:
The matrix generated using concatenating has size:
 and generate a code
and generate a code 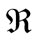 with the minimum distance
with the minimum distance , while a
, while a 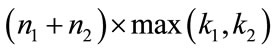 matrix generates a code
matrix generates a code  with the minimum distance:
with the minimum distance:
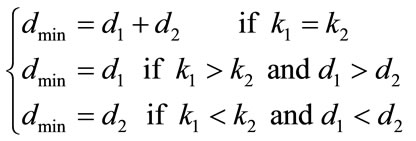
In the case of a 3 branches binary tree structure convolutional code, the generator matrix of the encoder can be written as:
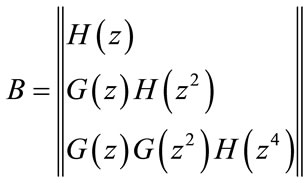
Corollary:
If 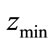 is the free distance of an encoder of generator matrix
is the free distance of an encoder of generator matrix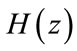 , the free distance of its component
, the free distance of its component 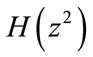 is
is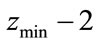 .
.
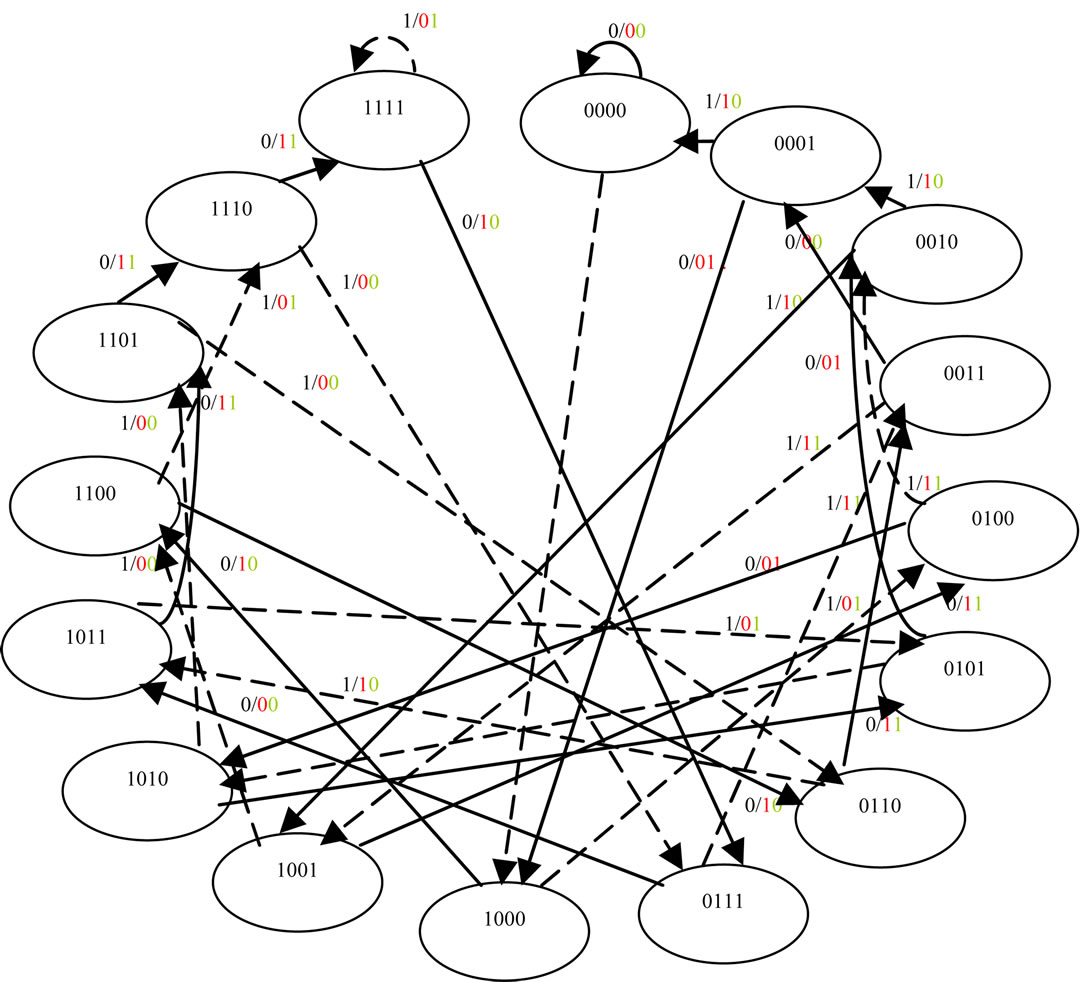
Figure 15. Multiresolution state diagram of the MR (37,21) convolutional code.
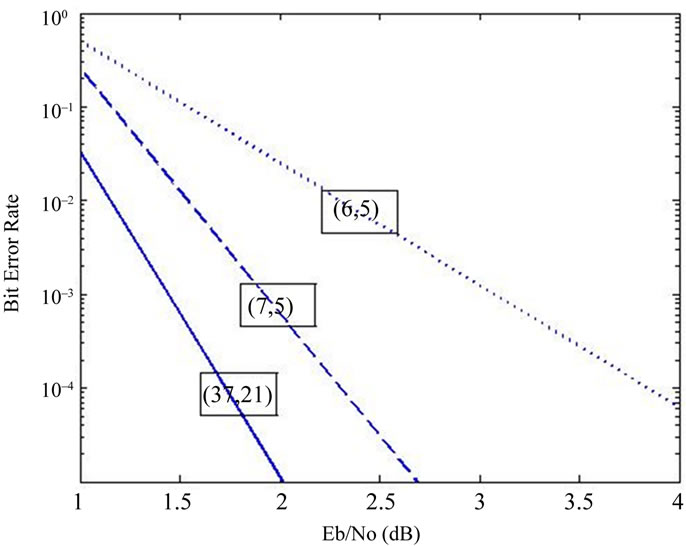
Figure 16. Theoritical bound for SR (37,21) TC and its MR (7,5) and (6,5) components.
Proof:
If  is the minimum free distance of the encoder with generator matrix
is the minimum free distance of the encoder with generator matrix 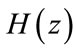 and degree N, then it coder component with generator matrix
and degree N, then it coder component with generator matrix 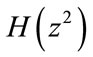 which has degree N – 2, therefore the minimum free distance is
which has degree N – 2, therefore the minimum free distance is .
.
Using the result from the corollary, we deduce that the free distance of the second branch in the multiresolution decomposition tree is: 
And the free distance for the third branch is:
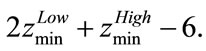
The distance of the branches decreases as the level of decomposition in the tree structure.
If the matrices G(z) and H(z) are appropriately designed, then, the encoder tree structure system produces perfect reconstruction that is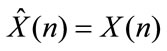 , in this case we get a quadrature Mirror coders (QMC), that is the two coders have equal free distance and generate the same protection, the generator matrix satisfies the power symmetric condition:
, in this case we get a quadrature Mirror coders (QMC), that is the two coders have equal free distance and generate the same protection, the generator matrix satisfies the power symmetric condition:
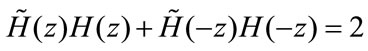
where  is the complex conjugation of H(z).
is the complex conjugation of H(z).
Under this condition, and if the remaining coders are chosen according to:

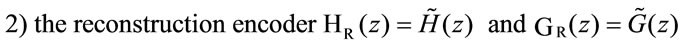 Then we have the Perfect reconstruction condition (Figure 17).
Then we have the Perfect reconstruction condition (Figure 17).
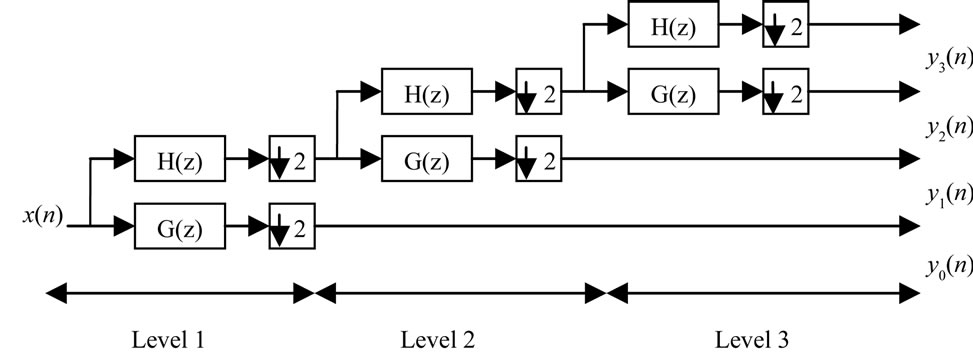
Figure 17. A three levels multiresolution decomposition tree code.
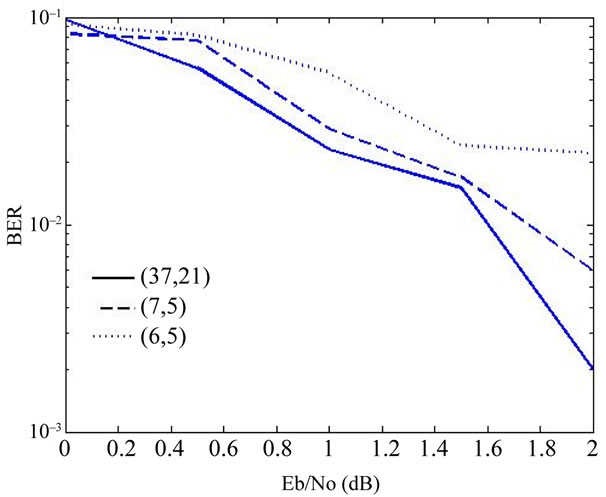
Figure 18. Performance of SR Turbo code and its HR and LR components for H.264/AVC UEP.
4.5. Experimental Results and Discussion
The Turbo Code of Berrou [15] is used for single resolution, its component are set with the same parameter with size interleaver 10. The two layered independents H264 streams are protected using different multi-resolution encoders , the HL component TC (7,5) present almost the same performance but at outstanding low cost and protecting the most valuable data (SPS, PPS and IDR) where it counterpart LL TC component (6,5) shows some degradation and is suitable for irrelevant data protection (Figure 18).
5. Conclusion
In this work we have investigated a multiresolution layered H.264/AVC OFDM scheme with a multiresolution modulation scheme in it base band domain followed by Time/frequency modulation in pass-band domain for the purpose to increase the performance of the OFDM overall system. First We have presented a mutiresolution source layered H.264/AVC data partition based on importance characteristics and then presented the design of the multiresolution constellation base band and the multiresolution OFDM pass band and showed its substantial superiority over single resolution in term of probability of bit error rate, channel capacity and spectral efficiency. We have investigated the multiresolution channel coding protection. We showed that the free distance of convolutional code is the sum of its multiresolution components, the protection of the multiresolution protection system decrease as we move through the levels of the decomposition tree. The free distance also decreased, we have simulated the multiresolution Turbo code for H.264/AVC UEP, and showed its prominent outperformance over the single resolution channel protection.
REFERENCES
- K. RamChandran, et al., “Muliresolution Broadcast for Digital HDTV Using Joint Source Channel Coding,” IEEE Journal on Selected Areas in Communication, Vol. 11, No. 1, 1993, pp. 6-23.
- T. Cover, “Broadcast Channels,” IEEE Transactions on Information Theory, Vol. 18, No. 1, 1972, pp. 2-14. doi:10.1109/TIT.1972.1054727
- T. Wiegand, G. J. Sullivan, G. Bjentegaard and A. Luthra, “Overview of the H.264/AVC Video Coding Standard,” IEEE Transactions on Circuits and Systems for Video Technology, Vol. 13, No. 7, 2003, pp. 560-576. doi:10.1109/TCSVT.2003.815165
- S. Kumar, L. Xu, M. K. Mandal and S. Panchanathan, “Error Resiliency Schemes in H.264/AVC Standard,” Journal of Visual Communication and Image Representation, Vol. 17, No. 2, 2006, pp. 425-450.
- Y. Dhondt and P. de Walle, “Flexible Macroblock Ordering an Error Resilience Tool in H264/AVC,” Fifth FTW Ph.D. Symposium, Faculty of Engineering, Ghent University, 2004.
- S. Ueda, H. Shigeno and K. I. Okada “NAL Level Stream Authentification for H.264/AVC,” IPSJ Digital Courier, Vol. 3, 2007, pp. 55-63. doi:10.2197/ipsjdc.3.55
- J. G. Proakis, “Digital Communications,” McGraw-Hill, New York, 1989.
- A. S. Saxena, “Embedded Multiresolution Signaling Scheme for CPFSK Modulation,” 2003. http://www.stanford.edu/~asaxena/resources/.../MRCPFSK_btech_thesis.pdf
- M. Pursley and J. Shea, “Nonuniform Phase-Shift-Key Modulation for Multimedia Multicast Transmission in Mobile Wireless Networks,” IEEE Journal on Selected Areas in Communication, Vol. 17, No. 5, 1999, pp. 774-783.
- M. Lallart, K. Nolan, P. Sutton and L. Doyle, “On-the -Fly Synchronization Using Wavelet and Wavelet Packet OFDM,” IEEE Signal Processing Letters, Vol. 12, 2005, pp. 577-580.
- H. Holms, M. M. Ghandi and E. V. Jones, “Spectral Efficiency of Variable-Rate Coded QAM for Flat Fading Channels,” IEEE Signal Processing Letters, Vol. 12, 2005, pp. 577-580.
- P. P. Vaidyanathan, “Multirate Systems and Filter Banks,” Prentice-Hall, Englewood Cliffs, 1992.
- G. Faria, J. A. Henriksson, E. Stare and P. Talmola, “DVB-H: Digital Broadcast Services to Handheld Devices,” Proceeding of the IEEE, Vol. 94, No. 1, 2006, pp. 194-209. doi:10.1109/JPROC.2005.861011
- S. Amir, A. Mehr, K. Nayebi and S. Kasaei, “Multirate Structures for Arbitrary Rate Error Control Coding,” 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 4, 2003, pp. 245-248.
- C. Berrou, A. Glavieux and P. Thitimajshima, “Near Shannon Limit Error-Correcting Coding and Decoding: Turbo Codes,” IEEE International Conference on Communications, Geneva, 23-26 May 1993, pp. 1064-1070.
- D. Divsalar, S. Doliar and F. Pollara, “Transfer Function Bounds on the Performance of Turbo Codes,” TDA Progress Report, Vol. 42, No. 122, 1995, pp. 44-45.
- S. Benedetto and G. Montorsi, “Unveilling Turbo Codes: Some Results on Parallel Concatenated Coding Schemes,” IEEE Transactions on Information Theory, Vol. 42, No. 2, 1996, pp. 409-428. doi:10.1109/18.485713
- S. Benedetto and G. Montorsi, “Design of Parallel Concatenated Convolutional Codes,” IEEE Transaction on Communications, Vol. 44, No. 5, 1996, pp. 591-600.
- E. Kuriata, “Creation of Unequal Error Protection Codes for Two Groups of Symbols,” International Journal of Applied Mathematics and Computer Science, Vol. 18, No. 2, 2008, pp. 251-257. doi:10.2478/v10006-008-0023-x

