Journal of Biomaterials and Nanobiotechnology
Vol.07 No.03(2016), Article ID:67685,15 pages
10.4236/jbnb.2016.73014
Measurement of Vibrational Stiffness and Air Damping of Damselfly Wings
Rupan Talukder, Kunigal N. Shivakumar
Center for Composite Materials Research (CCMR), Department of Mechanical Engineering, North Carolina A&T State University (NC A&T SU), Greensboro, North Carolina, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 February 2016; accepted 21 June 2016; published 24 June 2016
ABSTRACT
A simple cantilever beam vibration test method made of biomorph and insect wing, were used to measure the vibrational stiffness and the air damping of insect wings. Vibration tests were performed in vacuum pressures to atmosphere and the wing stiffness and air damping factor were measured. The test method was found to be a viable method for measuring wing stiffness, natural frequencies and mode shapes. The vibrational deformation of the insect wings was found to be combination of bending and torsion because of unsymmetrical geometry of wing. The measured stiffness (K) of damselfly wings varied from 0.18 to 0.31 N/m and the air damping ratio ranged from 0.72 to 0.79. The undamped natural frequency (fn) at 13 kPa varied from 249 to 299 Hz and at atmosphere it varied from 168 to 198 Hz.
Keywords:
Vibration, Natural Frequency, Stiffness, Damselfly Wing, Damping Ratio, Biomorph

1. Introduction
Insects like dragonflies and damselflies have attracted great interest as a model system for development of micro air vehicle (MAV). Dragonflies have amazing flying and hovering capabilities, namely, wings can flap at 35 Hz, can accelerate from 0 to 60 mph in 1 second [1] , and its lifting capability is about ten times that of an equivalent aircraft wing [2] . Damselflies have similar characteristics as dragonflies and its biological branch and species are Odonata and Lestessp, respectively [3] . Figure 1(a) shows four wings of a damselfly and Figure 1(b) shows an enlarged view of a typical wing and its important features, such as, veins, membrane, proximal and distal ends, and leading and trailing edges. The veins and membrane are formed by sun dried parts of blood vessels and muscles during the metamorphic transformation from larva to fly.

Figure 1. NC damselfly (a) and details of a sample wing (b).
The axial indentation [4] and tensile test [5] properties of damselfly veins and indentation properties of membrane [4] were measured and reported. Structural properties of wings are equally important to understand flying and hovering characteristics of damselfly. The properties include the vibrational stiffness, natural frequencies and associated mode shapes. Most of the works reported here to fore were focused on dragonfly and this was reviewed. Newman and Wooton [6] were the first to measure effective stiffness of dragonfly wing from a simple cantilever beam test by applying point load at the wing tip, at the distal ends. They found that the flexural stiffness was varied from 4 N/m to 16 N/m. Steppan [7] measured the flexural stiffness of a butterfly wing by applying line loading at 20%, 40%, 60%, 80% of the wing span from the support end (see Figure 2(a)). The flexural stiffness of dry and live samples ranged from 0.2 to 1.6 µNm2 and 0.2 to 0.6 µNm2, respectively. Steppan [7] found that the flexural stiffness of dry butterfly samples was higher than the live samples. Combes and Daniel [3] measured the flexural stiffness of the 16 species of insect wing by a cantilever beam test but applied a point force at 70% of the wing span and 70% of the chord length from the leading edge as shown in Figure 2(b). They showed that the flexure stiffness varied from 40 × 10−8 to 60 × 10−5 Nm2 and 7 × 10−8 to 1 × 10−5 Nm2 for spanwise and chordwise directions, respectively. Shang et al. [8] also measured the spanwise flexural stiffness of dragonflies at the same location but in upward direction and the values varied from 1 × 10−7 to 1 × 10−5 Nm2. Mengesha et al. [9] measured flexural stiffness of a butterfly wing and found flexure stiffness ranged from 10−6 to 1.7 × 10−6 Nm2. They also showed that the dry wings had higher stiffness than the live samples. Wang et al. [10] used a three-point bend test to measure the gross flexural modulus of the wing and it was varied from 25 to 35 GPa for forewing and 60 to 80 GPa for hindwing. All these tests were used to measure global flexural stiffness.
Insect wing is a dynamic component, required to know vibrational stiffness, natural frequency and mode shapes associated with the frequency. Chen et al. [11] used base-excitation model testing to measure the natural frequencies and mode shapes of dragonfly wing. They reported that fundamental natural frequency is about 170 Hz, each mode shape contains both bending and twisting components, and material damping ratio is about 5%. Sudo et al. [12] used a cantilever vibration test with high speed imaging technique to measure change of amplitude of deformation with frequencies. Chen et al. [13] used the laser vibrometer and mini-shaker cantilever beam test and measured the natural frequency of the dragonfly wing vein. They showed that the loss of moisture content in veins increased the stiffness of the vein by about 20 times. The wing tests reported here to fore were all in the air; viscosity of air could alter the measured stiffness and damping ratio.
This paper presents a cantilever beam vibration test but in a controlled atmosphere condition so that the true stiffness, natural frequency and the air damping factor can be measured directly. The testing is performed on damselfly wings. Several damselflies were captured, all four wings of the flies are extracted using fine surgical knife, and wings are dried in desiccators to extract any moisture. The dry wings are tested as a cantilever beam vibration setup excited by a biomorph at different vacuum pressure ranged from 101 kPa (atmosphere) and 13 kPa (about no air damping). High speed camera is used for recording the mode shapes. Measured natural frequencies are used to calculate stiffness and air damping using 1-D damped vibrational model.
2. Sample Preparation
Damselflies were caught from nearby watershed area at North Carolina A&T campus and wings were severed from body cuticle by a sharp surgical knife. The four wings of damselfly are represented by Left Forewing: LF; Left Hindwing: LH; Right Forewing: RF and Right Hindwing: RH. All four wings are shown in Figure 1(a). The fly wing specimen were designated by fly#XY; where fly# is 1 to 5 that represent the fly number, X is for L (Left) or R (Right) and Y is for F (Forewing) and H (Hindwing). For example the test specimen 1LF means fly#

Figure 2. Flexure stiffness measurement techniques. (a) Deflection from rectilinear loading [7] and (b) Deflection from a point loading [3] .
is 1 and the specimen wing is left and fore. After severing, attached muscle was trimmed carefully so that all sticky wet muscles were removed. A separate mass loss study was conducted for 1000 hours by recording mass at regular interval and found that, after10 hours of desiccation, the wing lost about 20% mass and then remained nearly constant with drying time. Therefore, 10 hours drying is used as a baseline for preparation of dry samples. The Figure 3 shows the schematic of the prepared wing specimen. The wing length WL and the cord length CL were measured by digital vernier calipers and the values were recorded for all flies in Table 1. The chord lengths were measured at three different locations (see Figure 3) and the maximum value was taken as the chord length. Mass of the wing was measured by an analytical balance with a resolution of 0.01 mg and is listed in Table 1. Variation of the wing length within a fly is less than 5% and among all five flies it is also less than 5%. The chord length of all flies is nearly same. This data shows that flies are nearly same size and/or age group. The average mass and STD (Standard Deviation) are listed in Table 1.
Figure 3. Schematic of trimmed wing from the body cuticle of the damselfly and measurement of wing and chord length.
3. One-Dimensional Vibrational Analysis
The methodology of determining wing stiffness, natural frequency, mode shape and damping consists of two steps. One, a cantilever beam wing test to measure the natural frequency and mode shapes. Then, the measured natural frequencies at different vacuum pressure were used to calculate the stiffness and air damping. In both cases a single degree of freedom model was used. Figure 4 shows a vibration test setup of the damselfly wing. Proximal end of the wing was attached to a PZT biomorph, which in turn attached to a stiff clamp with top and bottom rubber pad. By excitation of biomorph, the wing was vibrated (see Figure 4). When the exciter frequency matches the natural frequency of the wing, the amplitude of vibration was the largest.
The perfect vacuum condition was assumed to be at the air pressure of 13 kPa (limitation of the experimental setup), where the air damping was assumed to be zero and the measured natural frequency was considered as the undamped natural frequency (fn). The stiffness correspond to this condition was the true stiffness. Reaching perfect vacuum in a sample like this was difficult therefore 13 kPa pressure was assumed to be the perfect vacuum condition. However these results could be scaled if a perfect vacuum test data is available. The undamped natural frequency is represented by fn and natural frequency at any other pressure is by fd (air damped frequency). A single degree of freedom model represented by spring-mass and damper shown in Figure 5 is used to derive relationship among natural frequency (fd), stiffness (K) and damping factor (C).
The undamped system, shown in Figure 5(a), is represent for the vacuum (13 kPa) condition and the damped system is shown in Figure 5(b), which represent atmosphere (101 kPa) or to any other partial vacuum conditions. The air damping factor (C) at any partial vacuum is determined from the measured natural frequencies fn and fd. The spring stiffness, K, represents the stiffness due to bending and torsional deformations of the wing. The effective mass (Me) is defined by Me = αM, where α is the geometric constant, needs to be established by a complete modeling of this damselfly wing. The value of α for a cantilever beam of uniform mass along the
Figure 4. Schematic of the vibration test of damselfly wing.

Figure 5. Single degree of freedom representation of the experiment setup. (a) Undamped system; (b) Damped system.
length is 0.243 [14] [15] and it would be different for mass distribution along the wing length. However, for simplicity α = 0.243 used in the computation. The natural frequency (fn) of the undamped system (Figure 5(a)) [16] is:
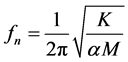 (1)
(1)
From the measured natural frequency (fn) of the beam at 13 kPa pressure, the true stiffness of the wing, K is calculated by the equation:
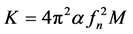 (2)
(2)
Then the damping factor (C) of a damped system (see Figure 5(b)) is calculated from fn and fd using the following equations [16] .
Table 1. The wing mass, wing length and chord length of damselflies.
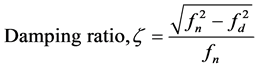 (3)
(3)
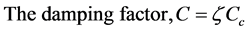 (4)
(4)
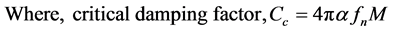 (5)
(5)
By conducting the vibration test in air and vacuum, the air damping factor is calculated. Similarly, by performing the vibration test at different partial vacuum, the damping factor at that air pressure is determined. The damped stiffness (Kd) of the system (see Figure 5(b)) is calculated by replacing the model as shown in Figure 5(b) and determining the damped natural frequency (fd) from the experiment. Then damped stiffness (Kd) is determined by the following equation:
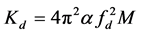 (6)
(6)
4. Vibration Test
4.1. Experimental Setup
Define Commercial biomorph (PL112.10 Bender Actuator supplied by Physik Instrumente, Karlsruhe, Germany), made from piezo actuator was used with suitable switching circuit to flap the wings at different frequencies. Proximal end of the wing was attached to the biomorph using gorilla glue (see Figure 6(b)). The wing-bio- morph assembly was held by a stiff clip with a rubber pad (see Figure 6(a)). The biomorph-wing was actuated by the waveform generator and DC power supply. Details of the test setup are shown in Figure 6. Tests in the atmospheric condition was performed on a laboratory table and tests in vacuum was conducted by placing the wing assembly inside a glass jar with controlled vacuum pressure as shown in Figure 7.
The glass jar and the lid were sealed by a silicon lubricant (Dow Corning’s high vacuum grease). The jar was connected to a rotor pump to evacuate and/or control the air pressure. The evacuating hose had a controlling hole that was used to control the air pressure inside the jar. The tests conducted outside the jar is called “atmospheric (Atm) test” and the tests conducted inside the jar is called “partial vacuum tests”. The test range was selected from 101 to 13 kPa. The 101 kPa represents the atmospheric pressure and 13 kPa represents the vacuum
Figure 6. Vibration test in atmospheric condition.
Figure 7. Vibration test in partial vacuum condition.
condition or the air damping is zero (base line). The material damping in the wing is neglected in this study. Reaching perfect vacuum was difficult in our equipment therefore, 13 kPa pressure was assumed as the base, here the air damping is assumed to be very small or zero. If the perfect vacuum can be achieved, then the results can be recalibrated using the Equation (3). The measured natural frequency at 13 kPa is considered the natural frequency (fn) of the wing and associated true stiffness (K), which is calculated from the Equation (2). The frequency and the associated stiffness at any vacuum pressure are represented as the damped frequency (fd) and the damped stiffness (Kd).
4.2. Test Procedure
Tests were conducted in the atmosphere (on a laboratory bench top) and inside the glass chamber, where the air pressure controlled by evacuating the air. In the glass chamber the pressure is varied from 101 kPa (atmospheric) to 13 kPa (minimum pressure that we can operate). Details of testing in these conditions are presented here.
4.2.1. Atmospheric Condition
The test was conducted on a laboratory bench in an undisturbed air condition. The biomorph-wing was connected to wave generator and power supply and the peak to peak voltage (VPP) was set to 1.5 volts. Before the biomorph-wing test was conducted, the test was validated with the 3 mil thick aluminum foil supplied by McMaster-Carr. The biomorph resonance frequency was 660 Hz and hence the test was limited to 500 Hz. The frequency of excitation of the biomorph was varied from 0 to 500 Hz; deformation modes of the wing were monitored. As the excitation frequency increased, the wing deformed in a combination of bending and torsional modes, a schematic representation of plan form of the wing, bending deformation about y-axis and torsional deformation about the x-axis are shown in Figure 8 in (a), (b) and (c), respectively.
The torsional deformation is caused by unsymmetrical geometry of the wing. The wing thickness tapers down from the leading edge to trailing edge as well as from the proximal end to distal end. As the excitation frequency increased, the amplitude of the bending deformation increased and reseeded after passing the natural frequency. Bending amplitude was easy to visually measure than the torsional rotation; therefore a vertical scale held by a stand was mounted close to the tip of the wing (see Figure 8(b)) to identify the natural frequency. During mounting the samples wing 2RH was damaged and wing 5RH was broke due to its delicacy, and fragileness. By closely monitoring the bending amplitude of the wing, the natural frequency was recorded. A careful trial and error experiment was done to identify the frequency precisely. The natural frequencies fn and fd of all four wing of five flies (4 × 5) are listed in third column of Table 2. The fd is called the air-damped natural frequency because the presence of air may change the natural frequency. The natural frequency fn varied from 211 Hz to 345 Hz, depending on the fly# and location of the wing.
Figure 8. Schematic diagram of bending and torsion deformation and mode shapes.
Table 2. Damping test results in atmospheric pressure.
The wing mode shapes of the wing were recorded by a high speed camera (Photron FASTCAM SA6, San Diego, California, USA). The camera was mounted at the level of the wing with a full focus on the wing tip. The Camera speed was set to 3000 fps (frames per second) so that enough images were recorded at 1920 × 1080 high density (HD) resolutions to get a clear view of the deformation. The mode shapes were recorded at the natural frequencies. For a wing natural frequency of about 250 Hz at 3000 fps of camera setting would results at least 12 images per cycle. The Figure 9 shows the front view of the deformed shapes of 1RF wing at 12 equally spaced time intervals and the pre and post images at the resonance. The deformed shapes at resonance were similar for all other wings.
4.2.2. Partial Vacuum Condition
The purpose of conducting this test was to measure the nearly true stiffness of the wing and the air damping factor at atmosphere as well as at other pressures. Here, we assume that the true stiffness of the wing and zero damping can be measured when the jar is in 100% vacuum. However, it was difficult to achieve full vacuum, therefore the pressure of 13 kPa was considered as the base line condition. The stiffness measured is assumed as the true stiffness and the damping is zero. The setup used was already described. The biomorph-wing assembly







Figure 9. One complete cycle at fundamental natural frequecny (262 Hz) of 1RF (Fly#1, Right Forewing), recorded at 3000 fps.
was kept inside of the glass jar and the test was conducted at different pressures (see Figure 7). A rotary pump was used to evacuate the air and the pressure inside the jar was measured by a pressure gauge (see Figure 7). The tests were conducted at five different pressures: 101 kPa (atmosphere), 81, 54, 27 and 13 kPa (base). Several validation tests were conducted to verify the reversibility and repeatability of the experiment. Then all 4 × 5 wings were tested at different air pressure. Among all 20 wings, the wing 5RH was broken during sample preparation and 2RH was damaged during the test. The measured natural frequencies for all wings are listed in Table 3
Table 3. Natural frequency and stiffness of damselfly wings in vacuum (13 kPa).
and deformation mode shapes at resonance were recorded and documented separately.
5. Results and Discussions
5.1. Repeatability and Reversibility of Test Results
Repeatability of measured natural frequency at different pressure was verified on four wings of fly#1. Table 4 lists, the measured natural frequencies 1LF wing at five pressure levels (101 to 13 kPa) at five different testing. The test was repeated five times with a time gap of about 15 minutes between each test cycle. The measured frequencies varied within ±1 Hz for all tests at a given pressure. These results confirm the repeatability of the test and fidelity of the test set-up and the instruments used.
The natural frequencies (fd) of 1LF and 1RF wings were measured by decreasing the air pressures from 101 kPa (atm) to 13 kPa and then reversed back from 13 kPa to 101 kPa. The variation of fd verses chamber air pressure for both descending and ascending pressures are shown in Figure 10. Except at 27 kPa all the natural frequencies were within ±1 Hz for a given pressure. The reason for this difference is not clear at this stage. Overall we can conclude that the results are reversible. Also note that the frequencies of 1LH and 1RH measured
Figure 10. Reversibility of natural frequencies at different vacuum pressure.
Table 4. Repeatability of natural frequency at different air pressure of 1LF.
*Atmospheric test (outside of jar); +Base pressure (no damping).
at atmosphere pressure within the jar and on the lab bench were same.
5.2. Determination of Wing Stiffness and Critical Damping Ratio
The true stiffness of the wing was calculated from Equation (2) and measured natural frequency (values in column 4 of Table 3) at 13 kPa pressure and assumed geometric factor α = 0.243. Then the critical damping factor (Cc), calculated from the Equation (5). The Table 3 lists the calculated true stiffness (K) and critical damping factor of the all 4 × 5 wings in columns 5 and 6, respectively. This stiffness is the combined stiffness of bending and torsional deformations as in mode shapes seen in Figure 8 and Figure 9. The stiffness varied among the four wings in a fly, while one would have thought they would be nearly same. Fore and hind wings of left and right wings have nearly same stiffness but with different values for fly#s 1, 2 and 3. Different flies can have different stiffness based on the environment that these biological insects raised and their ages. The average wing stiffness is about 0.3 N/m for fly# 2, 4 and 5 are nearly same, which indicate that they all belong to same group (age and the growth environment). The wing stiffness of fly#1 is the lowest (0.18 N/m). The average natural frequency (fn) of all fly wings is within the one standard deviation and the overall average is 279 Hz with standard deviation of 35 Hz. The natural frequency in air varies from 168 to 198 Hz for the five flies, with an average value 184 Hz and standard deviation 44 Hz. These results are in the same range (170 Hz) measured by Chen et al. [11] . The critical damping factor also followed the same trend as the stiffness. The average critical damping factor varied from 0.23 × 10−3 to 0.34 × 10−3 N-sec/m.
5.3. Determination of Air Damping Factor and Damping Ratio
The air damping ratio (ζ) and the damping factor (C) at atmosphere condition were calculated from Equations. (3) and (4), respectively. Using the measured natural frequency in atmosphere (fd) and natural frequency (fn) at 13 kPa are listed in Table 2. Calculated values of damping factor and ratio for all 4 × 5 wings are listed in Table 2. The average air damping ratio at atmospheric pressure varied from 0.72 to 0.79 with an overall value of 0.75 and standard deviation of 0.08. The air damping factor varied from 0.17 × 10−3 to 0.25 × 10−3 N-sec/m, with an overall value of 0.21 × 10−3 N-sec/m and standard deviation of 0.04 × 10−3 N-sec/m. The conclusion from this study is that the air damping ratio is quite considerable and cannot be neglected in modeling insect flight.
5.4. Variation Damping Ratio and Normalized Stiffness with Air Pressure
Damping ratio (ζ) at five different pressures are listed in Table 5 for all four wings of fly#1 along with natural frequencies (fd) at these pressures. As pressure decreased the wing natural frequency (fd) increased. Alternately the damping ratio (ζ) decreased; the highest is at atmosphere pressure (101 kPa). Except right hindwing (1RH), all three wings showed nearly same damping ratio at selected vacuum pressures. Variation of damping ratio with pressures for all four wings of fly #1 is shown in Figure 11(a). Average of 1LH, 1LF and 1RF wings is shown by solid symbol and a trend line through average values is shown by the solid line. The damping ratio decreased from 0.79 to 0 as the air pressure decreases from 101 to 13 kPa. The Figure 11(b) shows the variation of average damping ratio of all five flies and four wings of each fly. The error bar represents the 1-STD of data scatter.
Table 6 shows the list of normalized stiffness at five air pressures for all four wings of fly#1. The stiffness is normalized by the stiffness of the wing at air pressure to 13 kPa. As pressure decreased the normalized stiffness (Kd/K) increased for all wings, but the stiffness increasing rate is different for 1RH wing. Average of stiffness of 1LH, 1LF and 1RF are shown by solid symbols along with solid trend line with the air pressure as shown in Figure 12(a). The normalized average stiffness increased from 0.4 to 1.0 as the pressure decreased from 101 to 13 kPa. The Figure 12(b) shows the average values of all five flies along with the 1-STD data scatter. The average normalized stiffness is 0.44 at atmospheric pressure.
6. Concluding Remarks
A simple vibration test method to measure the vibrational stiffness and the air damping of insect wings was developed. The vibration mode of insect wings was found to be combination of bending and torsion deformations because of unsymmetrical wing configuration. The measured stiffness (K) of damselfly wings varied from 0.18 to 0.31 N/m and the average undamped natural frequency (fn) at 13 kPa varied from 249 to 299 Hz. Average air
Table 5. Summary of natural frequency and damping ratio of wings of fly#1 in different vacuum pressure.
Table 6. Stiffness of wings of fly#1 in different vacuum pressures.


Figure 11. (a) Damping ratio vs. vacuum pressure of typical damselfly (Fly#01); (b) Variation of damping ratio with pressure for all 5 damselflies.
damped natural frequency (fd) varied from 168 to 198 Hz; this compared well with Chen et al., result 170 Hz for dragonfly. The results also showed that the air damping is important in insect flights and the damping ratio (ζ) ranged from 0.72 to 0.79 for five damselflies tested. Note that, vacuum condition was assumed at 13 kPa, which is 87% vacuum and would impact the measured natural frequency and the stiffness. However the results presented here could be corrected once the test is conducted in 100% vacuum. The error at 13 kPa is assumed to be minimal and neglected. In addition, the stiffness would also be affected by the “α” factor, which needs to be established by a separate analysis.
Acknowledgements
The authors want to acknowledge the financial support of Army Research Laboratory (ARL) through Micro Autonomous Systems and Technology grant number W911NF-08-2-004. Authors also acknowledge Dr. Lingaiah for helping on experimental setup and Dr. Asha Hall, Vehicle Technology Directorate of US Army Research


Figure 12. (a) Normalized stiffness vs. vacuum pressure of typical damselfly (Fly#01); (b) Variation of normalized stiffness with pressure for all 5 damselflies.
Laboratory for introducing to the use of biomorph.
Cite this paper
Rupan Talukder,Kunigal N. Shivakumar, (2016) Measurement of Vibrational Stiffness and Air Damping of Damselfly Wings. Journal of Biomaterials and Nanobiotechnology,07,127-141. doi: 10.4236/jbnb.2016.73014
References
- 1. Lingaiah, S. and Shivakumar, K.N. (2007) Ultra Light Weight Materials for Bio-Inspired Microsystems. 16th International Conference on Composite Materials, Kyoto, 8-13 July 2007.
- 2. Sun, J.Y., Pan, C.X., Tong, J. and Zhang, J. (2009) Coupled Model Analysis of the Structure and Nano-Mechanical Properties of Dragonfly Wings. IET Nanobiotechnology, 4, 10-18.
http://dx.doi.org/10.1049/iet-nbt.2009.0009 - 3. Daniel, T.L. and Combes, S.A. (2003) Flexurul Stiffness in Insect Wings I. Scaling and the Influence of Wing Venation. The Journal of Experimental Biology, 206, 2979-2987.
http://dx.doi.org/10.1242/jeb.00523 - 4. Talucdher, A.R., Yarmolenko, S., Lingaiah, S. and Shivakumar, K.N. (2011) Indentation Properties of NC Dragonfly Wing by Nanolndentation. 26th Annual Technical Conference of the American Society for Composites 2011 and the 2nd Joint US-Canada Conference on Composites, 1, 67-81.
- 5. Talucdher, R. and Shivakumar, K. (2013) Tensile Properties of Veins of Damselfly Wing. Journal of Biomaterials and Nanobiotechnology, 4, 247-255.
http://dx.doi.org/10.4236/jbnb.2013.43031 - 6. Newman, D.L. and Wootton, R.J. (1986) An Approach to the Mechanics of Pleating in Dragonfly Wing. Journal of Experimental Biology, 125, 361-372.
- 7. Steppan, S.J. (2000) Flexural Stiffness Patterns of Butterfly Wings (Papilionoidea). Journal of Research on the Lepidoptera, 35, 61-77.
- 8. Shang, J.K., Combes, S.A., Finio, B.M. and Wood, R.J. (2009) Artificial Insect Wings of Diverse Morphology for Flapping-Wing Micro Air Vehicles. Bioinspiration & Biomimetics, 4, 036002.
http://dx.doi.org/10.1088/1748-3182/4/3/036002 - 9. Mengesha, T.E., Vallance, R.R. and Mittal, R. (2011) Stiffness of Desiccating Insect Wings. Bioinspiration & Binmimetics, 6, 014001.
http://dx.doi.org/10.1088/1748-3182/6/1/014001 - 10. Wang, X.-S., Li, Y. and Shi, Y.-F. (2008) Effects of Sandwich Microstructures on Mechanical Behaviors of Dragonfly Wing Vein. Composites Science and Technology, 68, 186-192.
http://dx.doi.org/10.1016/j.compscitech.2007.05.023 - 11. Chen, J.-S., Chen, J.-Y. and Chou, Y.-F. (2007) On the Natural Frequencies and Mode Shapes of Dragonfly Wings. Journal of Sound and Vibration, 313, 643-654.
http://dx.doi.org/10.1016/j.jsv.2007.11.056 - 12. Sudo, S., Takagi, K., Tsuyuki, K., Yano, T. and Nishida, K. (2008) The Dragonfly Flight by a Pair of Wings and Frequency Characteristics of Wings. Proceeding of XIth International Congress and Exposition, Orlando, 2-5 June 2008.
- 13. Chen, Y.H., Skote, M., Zhao, Y. and Huang, W.M. (2013) Stiffness Evaluation of the Leading Edge of the Dragonfly Wing via Laser Vibrometer. Materials Letters, 97, 166-168.
http://dx.doi.org/10.1016/j.matlet.2013.01.110 - 14. Shivakumar, K.N., Elber, W. and Illg, W. (1985) Prediction of Impact Force and Duration Due to Low-Velocity Impact on Circular Composite Laminates. Journal of Applied Mechanics, 52, 674-680.
http://dx.doi.org/10.1115/1.3169120 - 15. Akangah, P., Lingaiah, S. and Shivakumar, K. (2009) Effect of Nylon-66 Nano-Fiber Interleaving on Impact Damage Resistance of Epoxy/Carbon Fiber Composite Laminates. Composite Structures, 92, 1432-1439.
http://dx.doi.org/10.1016/j.compstruct.2009.11.009 - 16. Meirovitch, L. (1975) Elements of Vibration Analysis. McGraw-Hill, New York.
















